1.1锐角三角函数课件
图片预览


文档简介
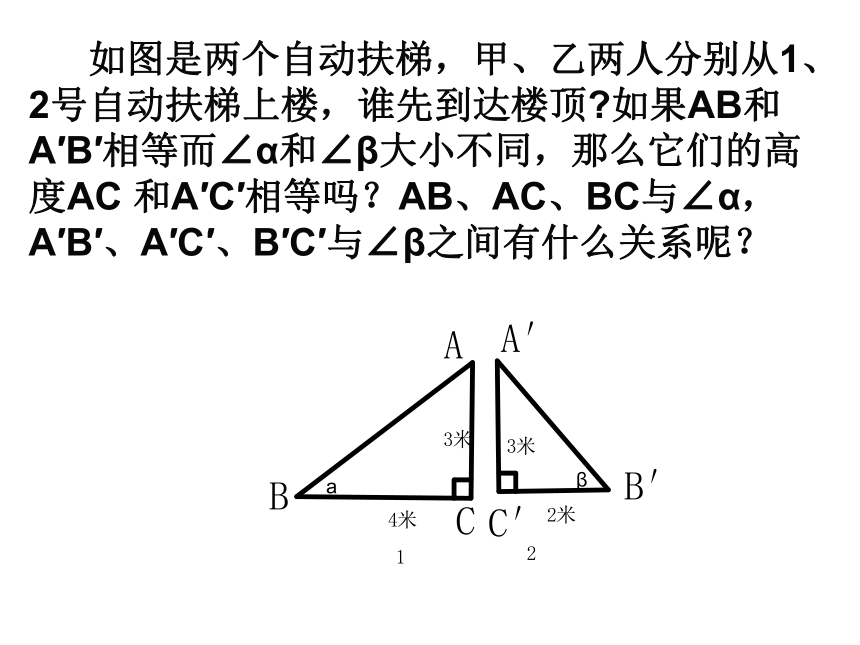
课件16张PPT。 如图是两个自动扶梯,甲、乙两人分别从1、2号自动扶梯上楼,谁先到达楼顶?如果AB和A′B′相等而∠α和∠β大小不同,那么它们的高度AC 和A′C′相等吗?AB、AC、BC与∠α,A′B′、A′C′、B′C′与∠β之间有什么关系呢?锐角三角函数(一) AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
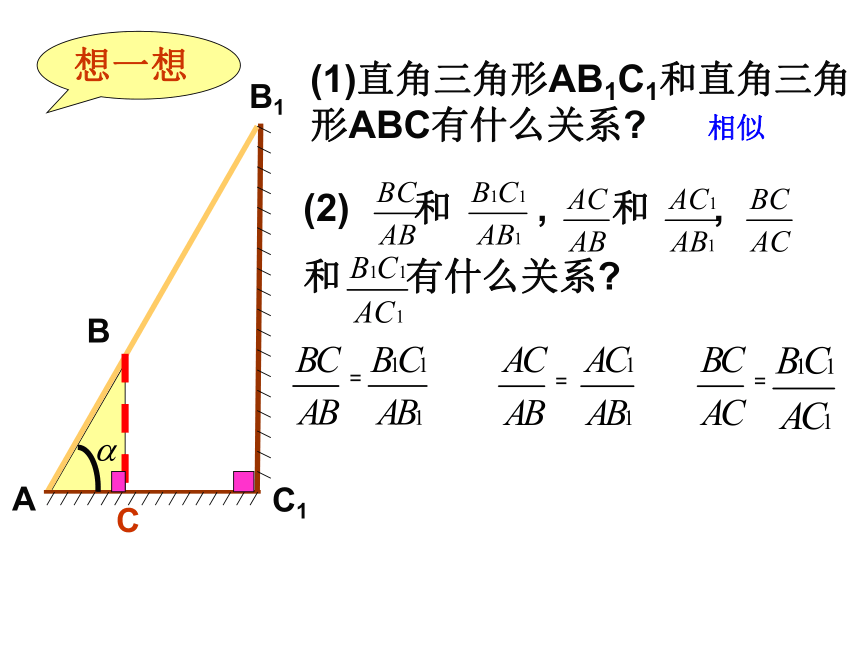
和 有什么关系? 相似 AB1 C1想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
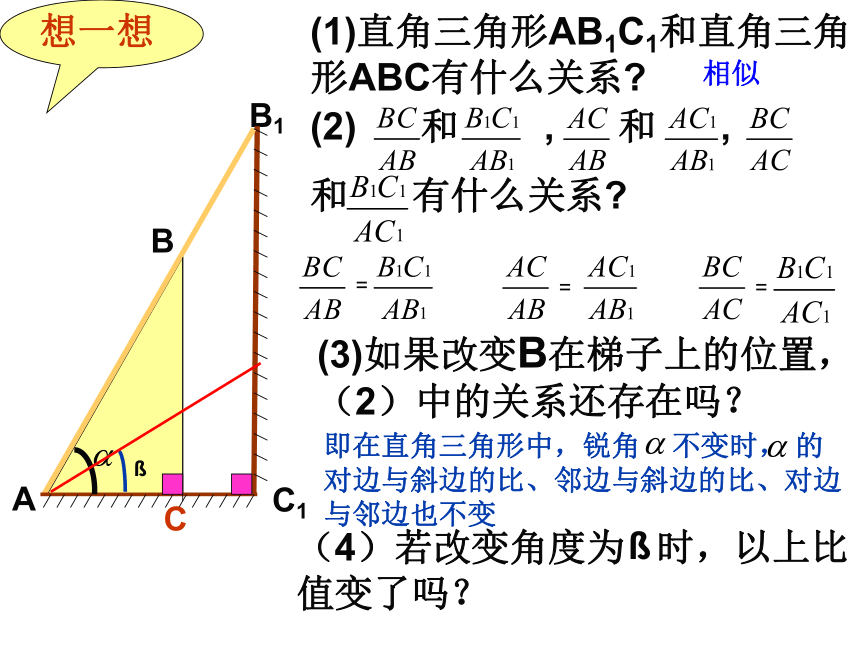
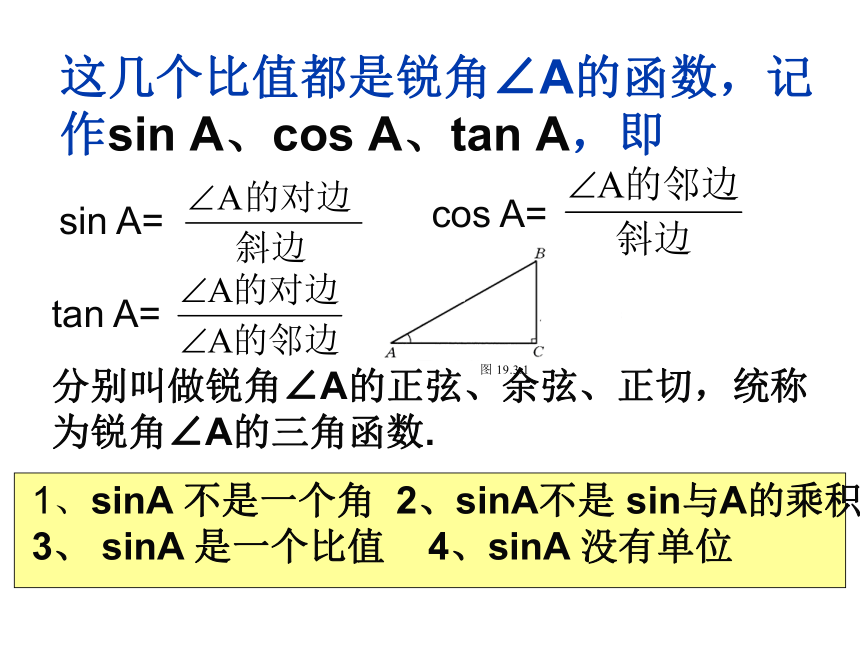
和 有什么关系? (3)如果改变B在梯子上的位置,(2)中的关系还存在吗??相似即在直角三角形中,锐角 不变时, 的对边与斜边的比、邻边与斜边的比、对边与邻边也不变(4)若改变角度为 时,以上比值变了吗??对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的结论这几个比值都是锐角∠A的函数,记作sin A、cos A、tan A,即 sin A= cos A= tan A= 分别叫做锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.1、sinA 不是一个角 2、sinA不是 sin与A的乘积
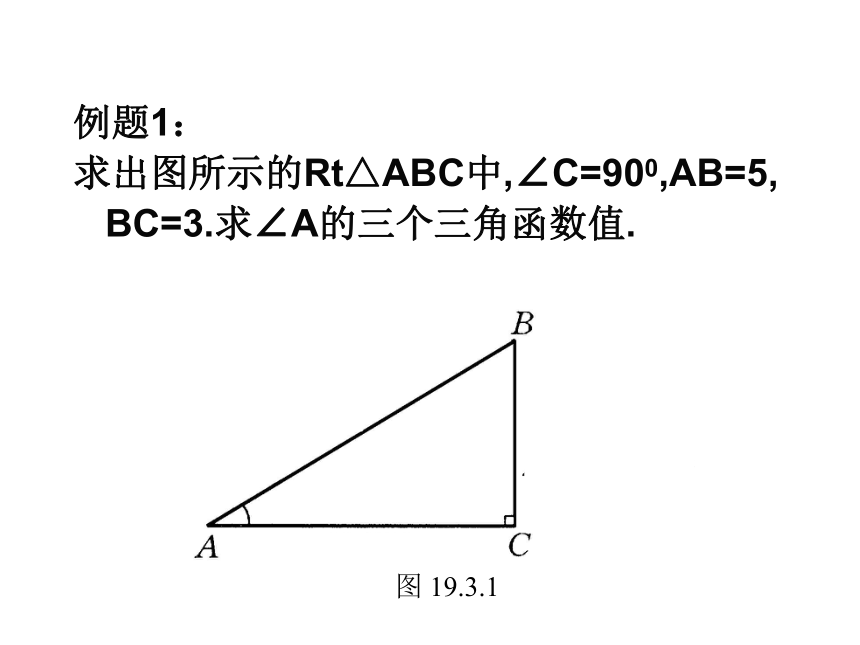
3、 sinA 是一个比值 4、sinA 没有单位例题1:
求出图所示的Rt△ABC中,∠C=900,AB=5,
BC=3.求∠A的三个三角函数值.例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.求:BC的长.理解定义: 你能利用直角三角形的三边关系得到sinA与 cosA的取值范围吗?0<sin A<1,0<cos A<1 练习:1、下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。2、1题中如果CD=5,AC=10,则sin∠ACD=
sin ∠DCB= 如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB
提示:过点A作AD垂直于BC于D.拓展延伸sinA=cosB ,cosA=sinB (∠A+∠B=90。)回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的正切,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.再见教学目标:
1.经历锐角的正弦、余弦和正切的探索过程,了解三角函数的概念。
2.掌握正弦、余弦和正切的符号,会用符号表示一个锐角的三角函数。
3.掌握在直角三角形中,锐角三角函数与边之比的关系。
4.了解锐角的三角函数值都是正实数,会根据锐角三角函数的定义求锐角三角函数值.
重点和难点:
1.本节教学的重点是锐角的正弦、余弦和正切和锐角三角函数的概念。
2. 锐角三角函数是将与锐角有关的比值作定义,可本介绍了正弦、余弦和正切三类,无论从函数的意义还是锐角三角函数的符号,以及函数中以角为自变量,都有别于已学过的一次函数和二次函数,其概念比较抽象,是本节教学的难点。课后反思
和 有什么关系? 相似 AB1 C1想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(2) 和 , 和 ,
和 有什么关系? (3)如果改变B在梯子上的位置,(2)中的关系还存在吗??相似即在直角三角形中,锐角 不变时, 的对边与斜边的比、邻边与斜边的比、对边与邻边也不变(4)若改变角度为 时,以上比值变了吗??对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的结论这几个比值都是锐角∠A的函数,记作sin A、cos A、tan A,即 sin A= cos A= tan A= 分别叫做锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、 sinA 是一个比值 4、sinA 没有单位例题1:
求出图所示的Rt△ABC中,∠C=900,AB=5,
BC=3.求∠A的三个三角函数值.例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.求:BC的长.理解定义: 你能利用直角三角形的三边关系得到sinA与 cosA的取值范围吗?0<sin A<1,0<cos A<1 练习:1、下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。2、1题中如果CD=5,AC=10,则sin∠ACD=
sin ∠DCB= 如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB
提示:过点A作AD垂直于BC于D.拓展延伸sinA=cosB ,cosA=sinB (∠A+∠B=90。)回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的正切,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.再见教学目标:
1.经历锐角的正弦、余弦和正切的探索过程,了解三角函数的概念。
2.掌握正弦、余弦和正切的符号,会用符号表示一个锐角的三角函数。
3.掌握在直角三角形中,锐角三角函数与边之比的关系。
4.了解锐角的三角函数值都是正实数,会根据锐角三角函数的定义求锐角三角函数值.
重点和难点:
1.本节教学的重点是锐角的正弦、余弦和正切和锐角三角函数的概念。
2. 锐角三角函数是将与锐角有关的比值作定义,可本介绍了正弦、余弦和正切三类,无论从函数的意义还是锐角三角函数的符号,以及函数中以角为自变量,都有别于已学过的一次函数和二次函数,其概念比较抽象,是本节教学的难点。课后反思
