3.2 从有理数到实数 课件(共24张PPT)
文档属性
| 名称 | 3.2 从有理数到实数 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-15 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
3.2 实数
浙教版七年级上册数学
1
=
=
=
=
=
=
2
3
4
5
6
- =
- =
- =
- =
- =
- =
-7
-8
-9
-10
-11
-12
=
=
=
=
=
齐声朗读
1
1
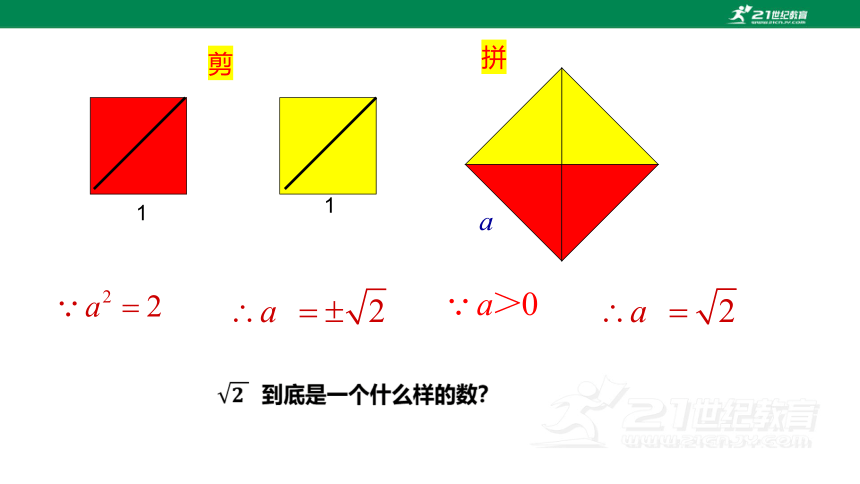
剪
拼
到底是一个什么样的数?
归纳: 既不是整数,也不是分数,所以不是有理数.
问题1: 可能是整数吗?
问题2: 可能是分数吗?
不是分数
探究1:的十分位是多少?
∵1.42=1.96, 1.52=2.25
∴1.4<<1.5
=1.4…
探究2:的百分位是多少?
∵1.412=1.9881, 1.422=2.0164
∴1.41<<1.42
=1.41…
探究……
=
1.41421356
2373095048801
68872420969807856967
187537694807317667973799073247
846210703885038753432764157273501
384623091229702492483605585073721264412149
709993583141322266592750559275579995050
11527820605714701095599716059702745345968620147285174186
4088919860955232923048430871432145083976260362799525140
798968725339654633180882964062061525835239505474575028775996172983557522
......
期待的循环,没有出现
不是整数,不是有限小数,也不是无限循环小数.
即不是有理数!!!!!!
我们把这种无限不循环小数叫做无理数.
(1)圆周率 及一些含有 的数都是无理数
例如:
(2)像 的数是无理数:
(3) 有一定的规律,但不循环的无限小数都是无理数。
例如:0.1010010001…〔两个1之间依次多1个0〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
开方开不尽:
2500年前毕达哥拉斯学派:
“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
学员希伯索斯 :
发现边长为1的正方形的对角线的长不能用有理数来表示
希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,
在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
无限的不能循环的小数——“无理数”。
是无理数!!!!!!
负有理数
实数的分类:
实数
有理数
无理数
正有理数
正有理数
有理数和无理数统称为实数
负有理数
无限不循环小数
零
有限小数和无限循环小数
0
1
2
3
-1
-2
-3
与 是互为相反数
-
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意义完全一样。
在实数范围内,每一个实数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数.我们说实数和数轴上的点是一一对应的.
正实数
0
负实数
例 把下列实数表示在数轴上,并比较它们的大小(用“<”连接)
,-π,1.5,-
解:
-3 -2 -1 0 1 2 3
-π
-
1.5
∴-π
在数轴上表示的两个实数,右边的数总比左边的数大.
像这种无限不循环小数叫做无理数.
常见的无理数有三种:
(1)开不尽方的数,
(2)含π的数,
π,3π,π+1.
(3)有规律但无限不循环的小数,
1.010010001…(两个1之间多一个“0”)
1.下列各数中,哪些是有理数?哪些是无理数?
3.14159, ,0.36,,2π,,
. .
有理数:
无理数:
3.14159
0.36
. .
2π
夯实基础,稳扎稳打
2.填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
3:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接):
-1.4、 、3.3、、 、1.5
4.判断下列说法是否正确,并举例说明理由。
(1)两个无理数的和一定是无理数;
(2)两个无理数的积一定是无理数;
与 -
与 -
与
与
5. 找出一个比-4大的无理数:_________.
或-π(答案不唯一)
6.在数轴上画出表示 - -1 的点.
解:以单位长度为边长画一个正方形如图,以 -1 为圆心,
正方形的对角线为半径画弧,与负半轴的交点就表示点- -1.
0
-1
-2
-3
1
-4
- -1
连续递推,豁然开朗
7.如图,表示 的点在数轴上哪两个字母之间( )
A.C与D B.A与B
C.A与C D.B与C
0
1
1.5
2
3
A
B
C
2.5
D
A
8. 设n为正整数,且n< <n+1,则n的值为( )
A.5 B.6 C.7 D.8
解析:根据特殊有理数找出最接近的完全平方数,问题可得到解决.∵ < < ,∴8< <9,∴n=8.
D
9.在哪两个相邻整数之间?在数轴上离哪一个整数更近?
()2
<
62
<
72
∵
∴
<
6
<
7
∵
()2
62
<
72
()2
∴
在数轴上离6更近
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2 实数
浙教版七年级上册数学
1
=
=
=
=
=
=
2
3
4
5
6
- =
- =
- =
- =
- =
- =
-7
-8
-9
-10
-11
-12
=
=
=
=
=
齐声朗读
1
1
剪
拼
到底是一个什么样的数?
归纳: 既不是整数,也不是分数,所以不是有理数.
问题1: 可能是整数吗?
问题2: 可能是分数吗?
不是分数
探究1:的十分位是多少?
∵1.42=1.96, 1.52=2.25
∴1.4<<1.5
=1.4…
探究2:的百分位是多少?
∵1.412=1.9881, 1.422=2.0164
∴1.41<<1.42
=1.41…
探究……
=
1.41421356
2373095048801
68872420969807856967
187537694807317667973799073247
846210703885038753432764157273501
384623091229702492483605585073721264412149
709993583141322266592750559275579995050
11527820605714701095599716059702745345968620147285174186
4088919860955232923048430871432145083976260362799525140
798968725339654633180882964062061525835239505474575028775996172983557522
......
期待的循环,没有出现
不是整数,不是有限小数,也不是无限循环小数.
即不是有理数!!!!!!
我们把这种无限不循环小数叫做无理数.
(1)圆周率 及一些含有 的数都是无理数
例如:
(2)像 的数是无理数:
(3) 有一定的规律,但不循环的无限小数都是无理数。
例如:0.1010010001…〔两个1之间依次多1个0〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
开方开不尽:
2500年前毕达哥拉斯学派:
“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
学员希伯索斯 :
发现边长为1的正方形的对角线的长不能用有理数来表示
希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,
在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
无限的不能循环的小数——“无理数”。
是无理数!!!!!!
负有理数
实数的分类:
实数
有理数
无理数
正有理数
正有理数
有理数和无理数统称为实数
负有理数
无限不循环小数
零
有限小数和无限循环小数
0
1
2
3
-1
-2
-3
与 是互为相反数
-
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意义完全一样。
在实数范围内,每一个实数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数.我们说实数和数轴上的点是一一对应的.
正实数
0
负实数
例 把下列实数表示在数轴上,并比较它们的大小(用“<”连接)
,-π,1.5,-
解:
-3 -2 -1 0 1 2 3
-π
-
1.5
∴-π
在数轴上表示的两个实数,右边的数总比左边的数大.
像这种无限不循环小数叫做无理数.
常见的无理数有三种:
(1)开不尽方的数,
(2)含π的数,
π,3π,π+1.
(3)有规律但无限不循环的小数,
1.010010001…(两个1之间多一个“0”)
1.下列各数中,哪些是有理数?哪些是无理数?
3.14159, ,0.36,,2π,,
. .
有理数:
无理数:
3.14159
0.36
. .
2π
夯实基础,稳扎稳打
2.填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
3:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接):
-1.4、 、3.3、、 、1.5
4.判断下列说法是否正确,并举例说明理由。
(1)两个无理数的和一定是无理数;
(2)两个无理数的积一定是无理数;
与 -
与 -
与
与
5. 找出一个比-4大的无理数:_________.
或-π(答案不唯一)
6.在数轴上画出表示 - -1 的点.
解:以单位长度为边长画一个正方形如图,以 -1 为圆心,
正方形的对角线为半径画弧,与负半轴的交点就表示点- -1.
0
-1
-2
-3
1
-4
- -1
连续递推,豁然开朗
7.如图,表示 的点在数轴上哪两个字母之间( )
A.C与D B.A与B
C.A与C D.B与C
0
1
1.5
2
3
A
B
C
2.5
D
A
8. 设n为正整数,且n< <n+1,则n的值为( )
A.5 B.6 C.7 D.8
解析:根据特殊有理数找出最接近的完全平方数,问题可得到解决.∵ < < ,∴8< <9,∴n=8.
D
9.在哪两个相邻整数之间?在数轴上离哪一个整数更近?
()2
<
62
<
72
∵
∴
<
6
<
7
∵
()2
62
<
72
()2
∴
在数轴上离6更近
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
