3.6圆内接四边形练习
图片预览

文档简介
选择题
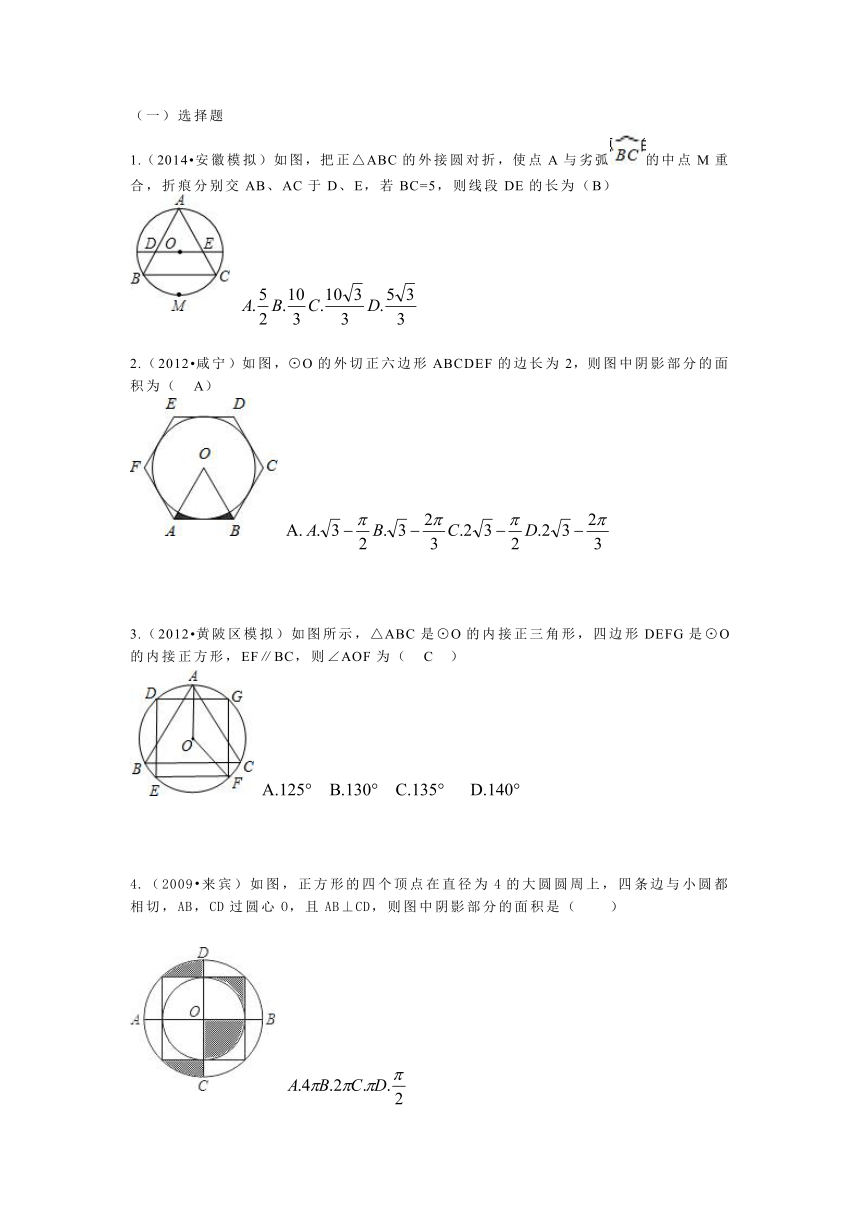
1.(2014 安徽模拟)如图,把正△ABC的外接圆对折,使点A与劣弧的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为(B)
(2012 咸宁)如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( A)
A.
(2012 黄陂区模拟)如图所示,△ABC是⊙O的内接正三角形,四边形DEFG是⊙O的内接正方形,EF∥BC,则∠AOF为( C )
A.125° B.130° C.135° D.140°
4.(2009 来宾)如图,正方形的四个 ( http: / / www.21cnjy.com )顶点在直径为4的大圆圆周上,四条边与小圆都相切,AB,CD过圆心O,且AB⊥CD,则图中阴影部分的面积是( )
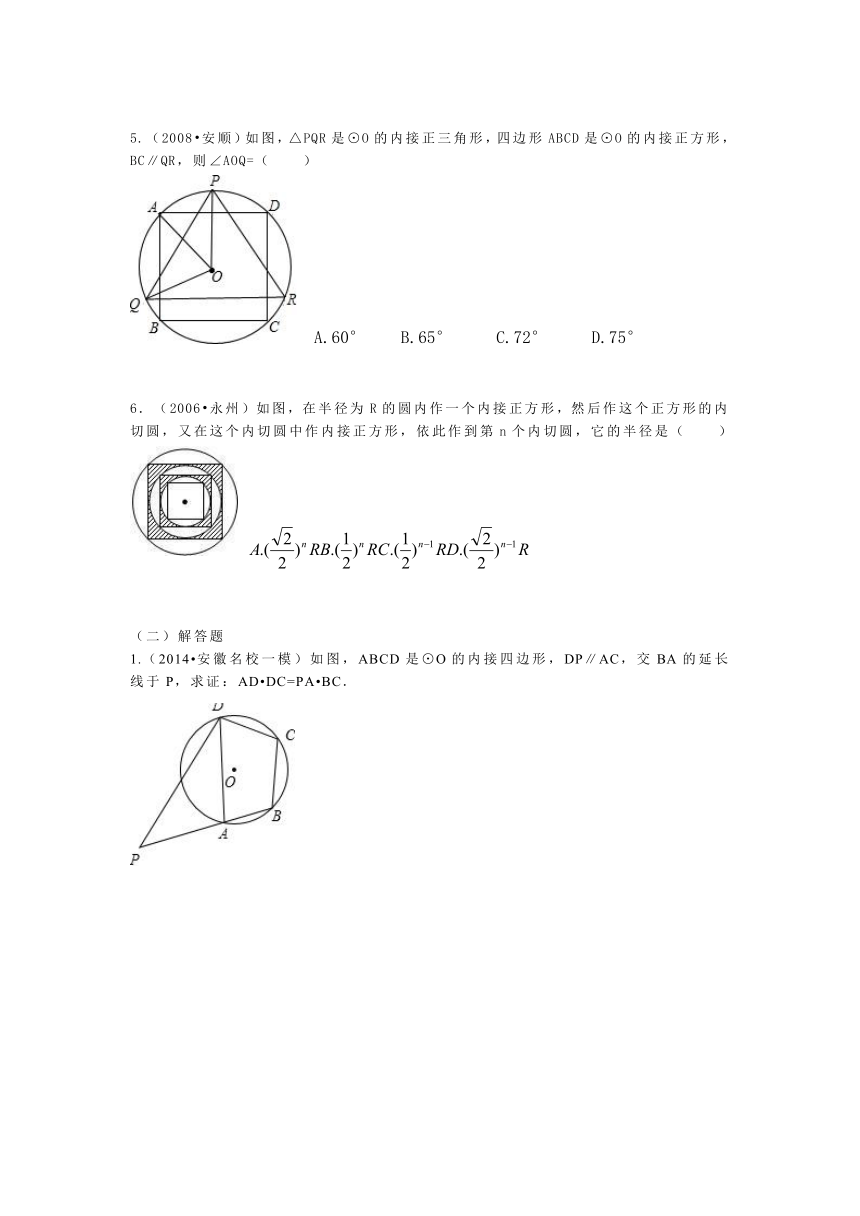
(2008 安顺)如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
(2006 永州)如图,在半径为R的圆内作 ( http: / / www.21cnjy.com )一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
(二)解答题
1.(2014 安徽名校一模)如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD DC=PA BC.
( http: / / www.21cnjy.com )
(2007 绵阳)如图,△ABC中,E、F ( http: / / www.21cnjy.com )分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
( http: / / www.21cnjy.com )
3.(2006 韶关)如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为
(1)求证:△CDE∽△CBA;
(2)求DE的长.
( http: / / www.21cnjy.com )
4.(2005 荆门)已知 ( http: / / www.21cnjy.com ),如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF
(1)求证:AB=AC;
(2)若AC=3cm,AD=2cm,求DE的长.
(2004 烟台)已知△ABC中,AB=AC,以AB为直径的圆O交BC于D,交AC于E,
(1)如图①,若AB=6,CD=2,求CE的长;
(2)如图②,当∠A为锐角时,使判断∠BAC与∠CBE的关系,并证明你的结论;
(3)若②中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图③,CA的延长线与圆O相交于E.
请问:∠BAC与∠CBE的关系是否与(2)中你得出的关系相同?若相同,请加以证明,若不同,请说明理由.
6.(2000 福建)已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.
求证:DE AB=BC CD.
7.如图1,已知△ABC,AB=AC, ( http: / / www.21cnjy.com )以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
(1)求证:DE=DC.
(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.
8.(1)已知:如图1,四边形AB ( http: / / www.21cnjy.com )CD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
如图,⊙O为四边形ABCD外接圆,其中=,其中CE⊥AB于E.
(1)求证:AB=AD+2BE;
(2)若∠B=60°,AD=6,△ADC的面积为,求AB的长.
(2012 江干区一模)如图,一只 ( http: / / www.21cnjy.com )纺锤可近似看作由两个圆锥拼合而成,AB=18,AD=9,r=3.
(1)求纺锤的表面积;
(2)一只蚂蚁要从C点出发绕这只纺锤爬一圈回到原地,求蚂蚁爬过的最短路线长.
11.(2010.桥西区模拟)如图,圆锥的底面半径为10cm,高为.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
1.(2014 安徽模拟)如图,把正△ABC的外接圆对折,使点A与劣弧的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为(B)
(2012 咸宁)如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( A)
A.
(2012 黄陂区模拟)如图所示,△ABC是⊙O的内接正三角形,四边形DEFG是⊙O的内接正方形,EF∥BC,则∠AOF为( C )
A.125° B.130° C.135° D.140°
4.(2009 来宾)如图,正方形的四个 ( http: / / www.21cnjy.com )顶点在直径为4的大圆圆周上,四条边与小圆都相切,AB,CD过圆心O,且AB⊥CD,则图中阴影部分的面积是( )
(2008 安顺)如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
(2006 永州)如图,在半径为R的圆内作 ( http: / / www.21cnjy.com )一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
(二)解答题
1.(2014 安徽名校一模)如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD DC=PA BC.
( http: / / www.21cnjy.com )
(2007 绵阳)如图,△ABC中,E、F ( http: / / www.21cnjy.com )分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
( http: / / www.21cnjy.com )
3.(2006 韶关)如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O的半径为
(1)求证:△CDE∽△CBA;
(2)求DE的长.
( http: / / www.21cnjy.com )
4.(2005 荆门)已知 ( http: / / www.21cnjy.com ),如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF
(1)求证:AB=AC;
(2)若AC=3cm,AD=2cm,求DE的长.
(2004 烟台)已知△ABC中,AB=AC,以AB为直径的圆O交BC于D,交AC于E,
(1)如图①,若AB=6,CD=2,求CE的长;
(2)如图②,当∠A为锐角时,使判断∠BAC与∠CBE的关系,并证明你的结论;
(3)若②中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图③,CA的延长线与圆O相交于E.
请问:∠BAC与∠CBE的关系是否与(2)中你得出的关系相同?若相同,请加以证明,若不同,请说明理由.
6.(2000 福建)已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.
求证:DE AB=BC CD.
7.如图1,已知△ABC,AB=AC, ( http: / / www.21cnjy.com )以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
(1)求证:DE=DC.
(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.
8.(1)已知:如图1,四边形AB ( http: / / www.21cnjy.com )CD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
如图,⊙O为四边形ABCD外接圆,其中=,其中CE⊥AB于E.
(1)求证:AB=AD+2BE;
(2)若∠B=60°,AD=6,△ADC的面积为,求AB的长.
(2012 江干区一模)如图,一只 ( http: / / www.21cnjy.com )纺锤可近似看作由两个圆锥拼合而成,AB=18,AD=9,r=3.
(1)求纺锤的表面积;
(2)一只蚂蚁要从C点出发绕这只纺锤爬一圈回到原地,求蚂蚁爬过的最短路线长.
11.(2010.桥西区模拟)如图,圆锥的底面半径为10cm,高为.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
同课章节目录
