第2章 简单事件的概率 单元检测能力提升卷(含解析)
文档属性
| 名称 | 第2章 简单事件的概率 单元检测能力提升卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 757.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 14:12:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2章 简单事件的概率 单元检测能力提升卷、
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列事件为随机事件的是( )
A.负数大于正数 B.三角形内角和等于180°
C.明天太阳从东方升起 D.购买一张彩票,中奖
2.盒子里有10个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大 C.不可能是黑球 D.摸出黄球的可能性最小
3.在一个不透明的袋子中装有3个红球,2个白球和4个黄球.每个球除颜色外其余均相同,从袋中随机摸出一个球,摸到红球的概率是( )
A. B. C. D.
4.如图,一只松鼠先经过第一道门(A,B或C),再经过第二道门(D或E)出去,则松鼠走出笼子的路线是“先经过A门,再经过E门”的概率是( )
A. B. C. D.
5.从长度为1cm,1cm,2cm,2cm的4条线段中任意选3条线段,这三条线段能够组成等腰三角形的概率是( )
A. B. C. D.
6.我国自古以来就有植树的传统,植树可以净化沙土,防止土地沙漠化,对于调节气候、涵养水源、减轻大气污染具有重要意义.在清明时节植树为最佳,因为此时的气候温暖,适宜树苗的成活.某林业局将一种树苗移植成活的情况绘制成如图统计图,由此可估计这种树苗移植成活的概率约为( )
A.0.80 B.0.85 C.0.90 D.0.95
7.以下说法合理的是( )
A.小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C.某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
8.如图所示,有一电路连着三个开关,每个开关闭合的可能性均为,若不考虑元件的故障因素,则电灯点亮的可能性为( )
A. B. C. D.
9.袋中有除颜色以外其余都相同的红球3个,黄球1个.从中任意摸出1个球,记下颜色后放回、摇匀,像这样先后摸球2次,摸到的都是红球,则第3次摸到红球的概率是( )
A.1 B.O C. D.
10.一个密码箱的密码由五位数字组成,每个数位上的数都是从0到9的自然数.小明只记得其中的三个数字,则他一次就能打开锁的概率为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.将一个正六面体骰子掷一次,它的点数恰好是4的概率是 .
12.文明出行,遵守交通规则“红灯停,绿灯行”.已知一个十字路口的交通信号灯每分钟红灯亮20秒,绿灯亮30秒,黄灯亮10秒,则当圆圆经过这个路口时,信号灯恰好是绿灯的概率为 .
13.一个袋子中有若干个白球和绿球,它们除了颜色外都相同.随机从中摸一个球,恰好摸到绿球的概率是,则袋子中至少有 个绿球.
14.在一个不透明的纸箱中装有4个白球和n个黄球,它们只有颜色不同.为了估计黄球的个数,杨老师进行了如下试验:每次从中随机摸出1个球,记下颜色后放回并摇匀.大量重复之后,杨老师发现摸到白球的频率稳定在附近,则n约为 .
15.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 .
16.学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1)下列事件中,哪些是必然事件?哪些是不可能事件?哪些是不确定事件?(填入题后括号内)
①校运会上,我班一位女同学的100米跑成绩是12秒11.( 事件)
②人在地球上所受的重力比在月球上小.( 事件)
③一个四边形四个内角的和等于360°.( 事件)
(2)写出一个不确定事件.(只需写一个,填在下面的横线上)
18.从一副普通的扑克牌中取出五张牌,它们的牌面数字分别是4,4,5,5,6.
(1)将这五张扑克牌背面朝上,洗匀后从中随机抽取一张,则抽取的这张牌的牌面数字是4的概率是多少?
(2)将这五张扑克牌背面明上,洗匀后从中随机抽取一张(不放回),再从中随机抽取第二张,请用列表或画树状图的方法,求抽取的这两张牌的牌面数字之和为奇数的概率.
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 b 295 480 601
摸到白球的频率 a 0.64 0.59 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)如果袋中有15个白球,那么袋中除了白球外,还有多少个其它颜色的球.
20.口袋里只有8个球,除颜色外都相同,其中有x个红球,y个白球,没有其他颜色的球,从中随意摸出一个球:(1)如果摸到红球与摸到白球的可能性相等,分别求x和y的值.
(2)在(1)的条件下,现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是,求取走多少个白球.
21.一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率;
(2)先从中任意摸出1个球,再从余下的2个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
22.工厂质检员对甲员工近期生产的产品进行抽检,统计合格的件数,得到如下表格:
抽取件数(件) 50 100 200 300 500 1000
合格频数 49 94 192 285 m 950
合格频率 0.98 0.94 0.96 0.95 0.95 n
(1)表格中m的值为 ,n的值为 .
(2)估计任抽一件该产品是不合格品的概率.
(3)该工厂规定,若每被抽检出一件不合格产品,需在相应员工奖金中扣除给工厂2元的材料损失费,今天甲员工被抽检了460件产品,估计要在他奖金中扣除多少材料损失费?
23.在学习概率的课堂上,老师提出问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
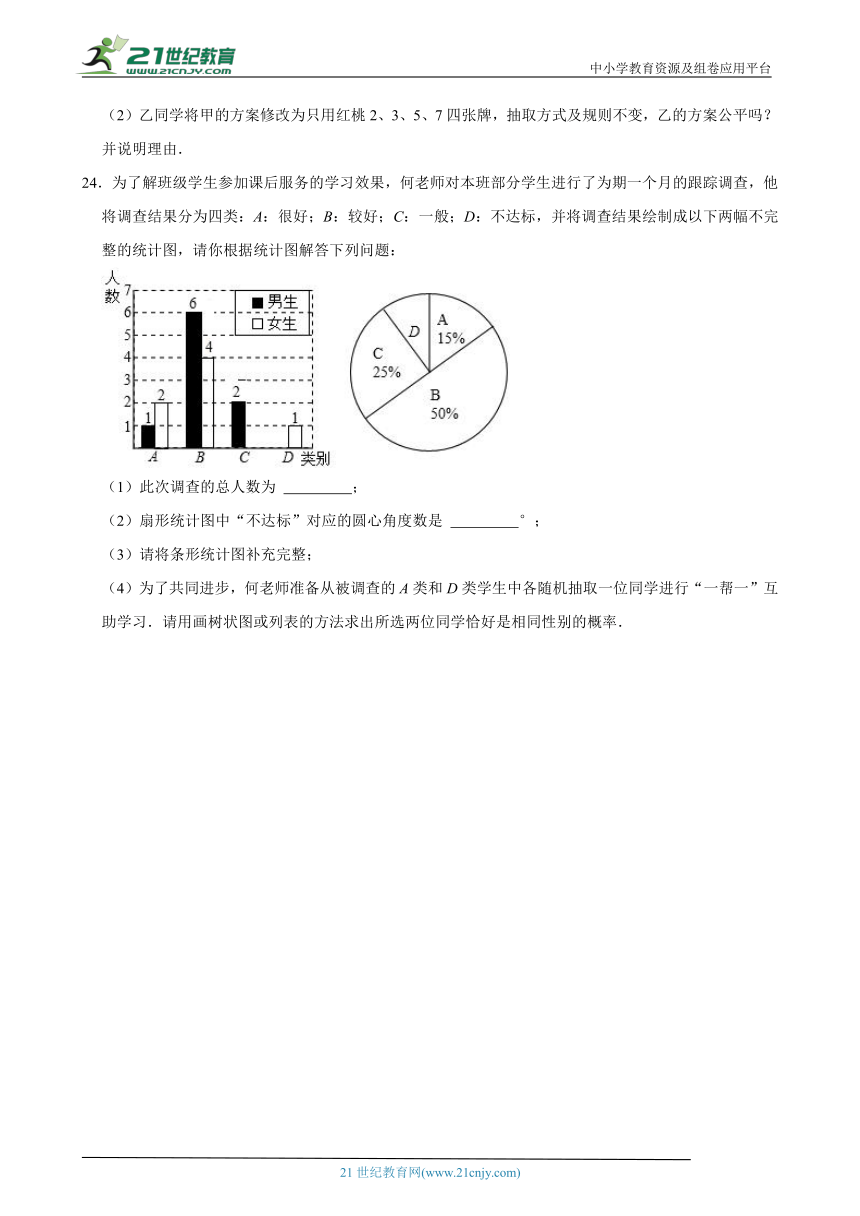
24.为了解班级学生参加课后服务的学习效果,何老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)此次调查的总人数为 ;
(2)扇形统计图中“不达标”对应的圆心角度数是 °;
(3)请将条形统计图补充完整;
(4)为了共同进步,何老师准备从被调查的A类和D类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列事件为随机事件的是( )
A.负数大于正数 B.三角形内角和等于180°C.明天太阳从东方升起 D.购买一张彩票,中奖
【点拨】根据已知条件,结合必然事件、随机事件、随机事件的定义即可求解.
【解析】解:A.负数大于正数是不可能事件,不符合题意;
B.三角形内角和等于180°是必然事件,不符合题意;
C.明天太阳从东方升起是必然事件,不符合题意;
D.购买一张彩票,中奖是随机事件,符合题意.
故选:D.
【点睛】本题主要考查必然事件、随机事件、随机事件的定义,属于基础题,理解相关概念是关键.
2.盒子里有10个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大 C.不可能是黑球 D.摸出黄球的可能性最小
【点拨】根据题意列出树状图求出各种颜色求得概率,逐个判断即可得到答案.
【解析】解:由题意可得,
摸出红球的概率为,摸出黄球的概率为:,摸出黑球的概率为:,
故选:B.
【点睛】本题考查概率定义及树状图法求概率,解题的关键是正确理解概率的定义.
3.在一个不透明的袋子中装有3个红球,2个白球和4个黄球.每个球除颜色外其余均相同,从袋中随机摸出一个球,摸到红球的概率是( )
A. B. C. D.
【点拨】根据概率的公式计算即可.
【解析】解:.
故选:B.
【点睛】本题主要考查了概率的公式,熟知:如果一个事件有n种可能,而且这些事件发生的可能性相同,其中事件A出现m种结果,那么事件A的概率为:.
4.如图,一只松鼠先经过第一道门(A,B或C),再经过第二道门(D或E)出去,则松鼠走出笼子的路线是“先经过A门,再经过E门”的概率是( )
A. B. C. D.
【点拨】画树状图列出所有等可能结果,从中找到松鼠走出笼子的路线是“先经过A门,再经过E门”的结果数,再根据概率公式求解即可.
【解析】解:画树状图如下:
共有6种等可能的结果,其中松鼠走出笼子的路线是“先经过A门,再经过E门”的只有1种结果,
所以松鼠走出笼子的路线是“先经过A门,再经过E门”的概率为,
故选:D.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
5.从长度为1cm,1cm,2cm,2cm的4条线段中任意选3条线段,这三条线段能够组成等腰三角形的概率是( )
A. B. C. D.
【点拨】利用完全列举法展示所有4种等可能的结果,然后根据等腰三角形的判定方法和概率公式求解.
【解析】解:从4条线段中任意选3条线段的所有结果为1、1、2;1、1、2;1、2、2;1、2、2,共有4种等可能的结果,
其中这三条线段能够组成等腰三角形的结果数为2种,
所有这三条线段能够组成等腰三角形的概率==.
故选:A.
【点睛】本题考查了列表法与树状图法:利用完全列举法展示所有可能的结果.也考查了三角形三边的关系和等腰三角形的判定.
6.我国自古以来就有植树的传统,植树可以净化沙土,防止土地沙漠化,对于调节气候、涵养水源、减轻大气污染具有重要意义.在清明时节植树为最佳,因为此时的气候温暖,适宜树苗的成活.某林业局将一种树苗移植成活的情况绘制成如图统计图,由此可估计这种树苗移植成活的概率约为( )
A.0.80 B.0.85 C.0.90 D.0.95
【点拨】由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9.
【解析】解:这种树苗成活的频率稳定在0.9,成活的概率估计值约是0.90.
故选:C.
【点睛】本题考查了利用频率估计概率.由于树苗数量巨大,故其成活的概率与频率可认为近似相等.用到的知识点为:总体数目=部分数目÷相应频率.部分的具体数目=总体数目×相应频率.
7.以下说法合理的是( )
A.小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C.某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
【点拨】根据各个选项中的说法可以判断是否正确,从而可以解答本题.
【解析】解:小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是是错误的,3次试验不能总结出概率,故选项A错误,
某彩票的中奖概率是5%,那么买100张彩票可能有5张中奖,但不一定有5张中奖,故选项B错误,
某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是不正确,中靶与不中靶不是等可能事件,故选项C错误,
小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的可能性是,故选项D正确,
故选:D.
【点睛】本题考查利用频率估计概率,解答本题的关键是明确题意,可以判断各个选项中的说法是否正确.
8.如图所示,有一电路连着三个开关,每个开关闭合的可能性均为,若不考虑元件的故障因素,则电灯点亮的可能性为( )
A. B. C. D.
【点拨】用列举法列举出可能出现的情况,在根据概率公式求解即可.
【解析】解:由于每个开关闭合的可能性均为,则共有8种情况;
1、K1关、K2关、K3开;
2、K1关、K2关、K3关;
3、K1关、K2开、K3开;
4、K1关、K2开、K3关;
5、K1开、K2开、关K3;
6、K1开、K2关、K3关;
7、K1开、K2开、K3开;
8、K1开、K2开、K3关.
只有5、7、8电灯可点亮,可能性为.
故选:C.
【点睛】本题考查的是可能性大小的判断,用到的知识点为:可能性等于所求情况数与总情况数之比.
9.袋中有除颜色以外其余都相同的红球3个,黄球1个.从中任意摸出1个球,记下颜色后放回、摇匀,像这样先后摸球2次,摸到的都是红球,则第3次摸到红球的概率是( )
A.1 B.O C. D.
【点拨】从中任意摸出1个球,有4种等可能结果,其中摸到红球的有3种结果,再根据概率公式求解即可.
【解析】解:从中任意摸出1个球,有4种等可能结果,其中摸到红球的有3种结果,
所以第3次摸到红球的概率是,
故选:C.
【点睛】本题主要考查概率公式,随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
10.一个密码箱的密码由五位数字组成,每个数位上的数都是从0到9的自然数.小明只记得其中的三个数字,则他一次就能打开锁的概率为( )
A. B. C. D.
【点拨】密码锁有五位数字组成,每一位数字都是0,1,2,3,4,5,6,7,8,9之中的一个,密码共100000种情况,小明只记得其中的三个数字,即有2个数字不准确共1000种情况;则他一次就能打开锁的概率为.
【解析】解:P(一次开锁)=.
故选:B.
【点睛】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率.
二、填空题:本题共6小题,每小题3分,共18分。
11.将一个正六面体骰子掷一次,它的点数恰好是4的概率是 .
【点拨】直接由概率公式求解即可.
【解析】解:∵掷一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子一次,它的点数恰好是4的情况有1种,
∴点数恰好是4的概率是,
故答案为:.
【点睛】本题考查了概率公式,熟记概率公式是解题的关键.
12.文明出行,遵守交通规则“红灯停,绿灯行”.已知一个十字路口的交通信号灯每分钟红灯亮20秒,绿灯亮30秒,黄灯亮10秒,则当圆圆经过这个路口时,信号灯恰好是绿灯的概率为 .
【点拨】直接利用概率公式可得答案.
【解析】解:经过这个路口信号灯是绿灯的概率是.
故答案为:.
【点睛】本题考查概率公式,熟练掌握概率公式是解答本题的关键.
13.一个袋子中有若干个白球和绿球,它们除了颜色外都相同.随机从中摸一个球,恰好摸到绿球的概率是,则袋子中至少有 3 个绿球.
【点拨】直接由概率公式即可得出结论.
【解析】解:∵一个袋子中有若干个白球和绿球,随机从中摸一个球,恰好摸到绿球的概率是,
∴袋子中至少有3个绿球,
故答案为:3.
【点睛】本题考查了概率公式:概率=所求情况数与总情况数之比.熟记概率公式是解题的关键.
14.在一个不透明的纸箱中装有4个白球和n个黄球,它们只有颜色不同.为了估计黄球的个数,杨老师进行了如下试验:每次从中随机摸出1个球,记下颜色后放回并摇匀.大量重复之后,杨老师发现摸到白球的频率稳定在附近,则n约为 8 .
【点拨】根据概率与频率的关系求解.
【解析】解:由题意得:=,
解得:n=8,
经检验:n=8是原分式方程的解,
故答案为:8.
【点睛】本题考查了利用频率估计概率,掌握频率与概率的关系是解题的关键.
15.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 .
【点拨】根据题意,可以画出相应的树状图,从而可以得到小乐抽到的两张邮票恰好是“立春”和“立夏”的概率.
【解析】解:设立春用A表示,立夏用B表示,秋分用C表示,大寒用D表示,画树状图如下,
由图可得,一共有12种等可能性的结果,
其中小乐抽到的两张邮票恰好是“立春”和“立夏”的可能性有2种,
∴小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是,
故答案为:.
【点睛】本题考查列表法与画树状图法求概率,解答本题的关键是明确题意,画出相应的树状图.
16.学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是 .
【点拨】画树状图,共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,然后由概率公式求解即可.
【解析】解:转盘B红色部分圆心角为240°,相当于2个蓝色部分,
画树状图如下:
共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,
∴小李同学同时转动A盘和B盘,她赢得游戏的概率是=.
【点睛】本题考查了树状图法求概率,正确画出树状图是解题的关键;用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1)下列事件中,哪些是必然事件?哪些是不可能事件?哪些是不确定事件?(填入题后括号内)
①校运会上,我班一位女同学的100米跑成绩是12秒11.( 不确定 事件)
②人在地球上所受的重力比在月球上小.( 不可能 事件)
③一个四边形四个内角的和等于360°.( 必然 事件)
(2)写出一个不确定事件.(只需写一个,填在下面的横线上) 明天会下雨(答案不唯一).
【点拨】根据事件发生的可能性大小判断即可.
【解析】解:(1)①校运会上,我班一位女同学的100米跑成绩是12秒11.(不确定事件)
②人在地球上所受的重力比在月球上小.(不可能事件)
③一个四边形四个内角的和等于360°.(必然事件)
(2)写出一个不确定事件.(只需写一个,填在下面的横线上) 明天会下雨(答案不唯一).
故答案为:(1)不确定,不可能,必然;(2)明天会下雨(答案不唯一).
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
18.从一副普通的扑克牌中取出五张牌,它们的牌面数字分别是4,4,5,5,6.
(1)将这五张扑克牌背面朝上,洗匀后从中随机抽取一张,则抽取的这张牌的牌面数字是4的概率是多少?
(2)将这五张扑克牌背面明上,洗匀后从中随机抽取一张(不放回),再从中随机抽取第二张,请用列表或画树状图的方法,求抽取的这两张牌的牌面数字之和为奇数的概率.
【点拨】(1)找出五张牌中,牌面数字为4的张数,求出抽取的这张牌的牌面数字是4的概率即可;
(2)列表得出所有等可能的情况数,找出抽取的这两张牌的牌面数字之和为奇数的情况数,即可求出所求.
【解析】解:(1)五张牌中,牌面数字分别是4,4,5,5,6,其中牌面数字为4的张数为2,
则P(牌面数字为4)=;
(2)列表如下:
4 4 5 5 6
4 ﹣﹣﹣ 8 9 9 10
4 8 ﹣﹣﹣ 9 9 10
5 9 9 ﹣﹣﹣ 10 11
5 9 9 10 ﹣﹣﹣ 11
6 10 10 11 11 ﹣﹣﹣
所有等可能的情况有20种,其中抽取的这两张牌的牌面数字之和为奇数的情况有12种,
则P(抽取的这两张牌的牌面数字之和为奇数)==.
【点睛】此题考查了列表法与树状图法,以及概率公式,用到的知识为:概率=所求情况数与总情况数之比.
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 b 295 480 601
摸到白球的频率 a 0.64 0.59 0.59 0.60 0.601
(1)上表中的a= 0.58 ,b= 118 ;
(2)“摸到白球”的概率的估计值是 0.6 (精确到0.1);
(3)如果袋中有15个白球,那么袋中除了白球外,还有多少个其它颜色的球.
【点拨】(1)利用频率=频数÷样本容量直接求解即可;
(2)根据统计数据,当n很大时,摸到白球的频率接近0.6;
(3)根据利用频率估计概率,可估计摸到白球的概率为0.6,然后利用概率公式计算其它颜色的球的个数.
【解析】解:(1)a=58÷100=0.58,b=200×0.59=118,
故答案为:0.58,118;
(2)由表格的数据可得,
“摸到白球的”的概率的估计值是0.6.
故答案为:0.6;
(3)15÷0.6﹣15=10(个),
答:除白球外,还有大约10个其它颜色的小球.
【点睛】本题考查了利用频率估计概率:大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
20.口袋里只有8个球,除颜色外都相同,其中有x个红球,y个白球,没有其他颜色的球,从中随意摸出一个球:(1)如果摸到红球与摸到白球的可能性相等,分别求x和y的值.
(2)在(1)的条件下,现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是,求取走多少个白球.
【点拨】(1)根据红球与白球的数量的情况即可求解;
(2)设取走x个白球,根据概率公式列出关于x的方程,解出x的值即可.
【解析】解:(1)∵摸到红球与摸到白球的可能性相等,且x+y=8,
∴x=y=4;
(2)设取走x个白球,放入x个红球,则口袋中现在有白球(4﹣x)个,红球(4+x)个,
根据题意得,=,
解得x=3,
答:取走3个白球.
【点睛】本题主要考查概率公式,随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
21.一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率;
(2)先从中任意摸出1个球,再从余下的2个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
【点拨】(1)直接利用概率公式求解;
(2)画树状图展示所有6种等可能的结果数,找出两次都摸到红球的结果数,然后根据概率公式求解.
【解析】解:(1)搅匀后从中任意摸出1个球,摸到红球的概率=;
故答案为:;
(2)画树状图为:
共有6种等可能的结果数,其中两次都摸到红球的结果数为2,
所以两次都摸到红球的概率==.
【点睛】此题考查列表法与树状图法,概率公式,解答本题的关键要熟练掌握概率的求法:概率=所求情况数与总情况数之比.
22.工厂质检员对甲员工近期生产的产品进行抽检,统计合格的件数,得到如下表格:
抽取件数(件) 50 100 200 300 500 1000
合格频数 49 94 192 285 m 950
合格频率 0.98 0.94 0.96 0.95 0.95 n
(1)表格中m的值为 475 ,n的值为 0.95 .
(2)估计任抽一件该产品是不合格品的概率.
(3)该工厂规定,若每被抽检出一件不合格产品,需在相应员工奖金中扣除给工厂2元的材料损失费,今天甲员工被抽检了460件产品,估计要在他奖金中扣除多少材料损失费?
【点拨】(1)根据频率=频数÷总数求解即可;
(2)用1减去合格品频率的稳定值即可;
(3)总数量乘以不合格品的概率,再乘以每件的损失费即可.
【解析】解:(1)m=500×0.95=475,n=950÷1000=0.95,
故答案为:475、0.95;
(2)1﹣0.95=0.05.
答:任抽一件该产品是不合格品的概率为0.05;
(3)460×0.05×2=46(元).
答:估计要在他奖金中扣除46元.
【点睛】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
23.在学习概率的课堂上,老师提出问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
【点拨】(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,比较即可.
(2)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,比较即可.
【解析】解:(1)甲同学的方案不公平.理由如下:
列表法,
小丽小芳 2 3 4 5
2 (2,3) (2,4) (2,5)
3 (3,2) (3,4) (3,5)
4 (4,2) (4,3) (4,5)
5 (5,2) (5,3) (5,4)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有8种,故小丽获胜的概率为:=,则小芳获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
(2)公平.理由如下:
列表如下:
小丽小芳 2 3 5 7
2 (2,3) (2,5) (2,7)
3 (3,2) (3,5) (3,7)
5 (5,2) (5,3) (5,7)
7 (7,2) (7,3) (7,5)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有:6种,故小丽获胜的概率为:=,则小芳获胜的概率为,
故此游戏两人获胜的概率相同,即他们的游戏规则公平.
【点睛】此题主要考查了游戏公平性,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合于两步或两步以上的完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
24.为了解班级学生参加课后服务的学习效果,何老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)此次调查的总人数为 20 ;
(2)扇形统计图中“不达标”对应的圆心角度数是 36 °;
(3)请将条形统计图补充完整;
(4)为了共同进步,何老师准备从被调查的A类和D类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.
【点拨】(1)根据A等级的人数和所占的百分比即可得出答案;
(2)用360°乘以“不达标”所占的百分比即可得出答案;
(3)先求出C等级的女生和D等级的男生,然后补全统计图即可;
(4)根据题意画出树状图得出所有等可能的情况数,找出符合条件的情况数,然后根据概率公式即可得出答案.
【解析】解:(1)调查的总人数为:3÷15%=20(人),
故答案为:20;
(2)360°×(1﹣50%﹣25%﹣15%)=36°,
答:扇形统计图中“课前预习不达标”对应的圆心角度数是36°;
故答案为:36;
(3)C等级的人数有:20×25%=5(人),
C等级的女生人数有:5﹣2=3(人),
D等级的男生人数有:20﹣(1+2+6+4+5+1)=1(人),
补全统计图如下:
(4)由题意画树形图如下:
从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选两位同学恰好是一位男同学和一位女同学的结果共有3种.
所以P(所选两位同学恰好是一位男同学和一位女同学)==.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第2章 简单事件的概率 单元检测能力提升卷、
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列事件为随机事件的是( )
A.负数大于正数 B.三角形内角和等于180°
C.明天太阳从东方升起 D.购买一张彩票,中奖
2.盒子里有10个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大 C.不可能是黑球 D.摸出黄球的可能性最小
3.在一个不透明的袋子中装有3个红球,2个白球和4个黄球.每个球除颜色外其余均相同,从袋中随机摸出一个球,摸到红球的概率是( )
A. B. C. D.
4.如图,一只松鼠先经过第一道门(A,B或C),再经过第二道门(D或E)出去,则松鼠走出笼子的路线是“先经过A门,再经过E门”的概率是( )
A. B. C. D.
5.从长度为1cm,1cm,2cm,2cm的4条线段中任意选3条线段,这三条线段能够组成等腰三角形的概率是( )
A. B. C. D.
6.我国自古以来就有植树的传统,植树可以净化沙土,防止土地沙漠化,对于调节气候、涵养水源、减轻大气污染具有重要意义.在清明时节植树为最佳,因为此时的气候温暖,适宜树苗的成活.某林业局将一种树苗移植成活的情况绘制成如图统计图,由此可估计这种树苗移植成活的概率约为( )
A.0.80 B.0.85 C.0.90 D.0.95
7.以下说法合理的是( )
A.小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C.某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
8.如图所示,有一电路连着三个开关,每个开关闭合的可能性均为,若不考虑元件的故障因素,则电灯点亮的可能性为( )
A. B. C. D.
9.袋中有除颜色以外其余都相同的红球3个,黄球1个.从中任意摸出1个球,记下颜色后放回、摇匀,像这样先后摸球2次,摸到的都是红球,则第3次摸到红球的概率是( )
A.1 B.O C. D.
10.一个密码箱的密码由五位数字组成,每个数位上的数都是从0到9的自然数.小明只记得其中的三个数字,则他一次就能打开锁的概率为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.将一个正六面体骰子掷一次,它的点数恰好是4的概率是 .
12.文明出行,遵守交通规则“红灯停,绿灯行”.已知一个十字路口的交通信号灯每分钟红灯亮20秒,绿灯亮30秒,黄灯亮10秒,则当圆圆经过这个路口时,信号灯恰好是绿灯的概率为 .
13.一个袋子中有若干个白球和绿球,它们除了颜色外都相同.随机从中摸一个球,恰好摸到绿球的概率是,则袋子中至少有 个绿球.
14.在一个不透明的纸箱中装有4个白球和n个黄球,它们只有颜色不同.为了估计黄球的个数,杨老师进行了如下试验:每次从中随机摸出1个球,记下颜色后放回并摇匀.大量重复之后,杨老师发现摸到白球的频率稳定在附近,则n约为 .
15.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 .
16.学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1)下列事件中,哪些是必然事件?哪些是不可能事件?哪些是不确定事件?(填入题后括号内)
①校运会上,我班一位女同学的100米跑成绩是12秒11.( 事件)
②人在地球上所受的重力比在月球上小.( 事件)
③一个四边形四个内角的和等于360°.( 事件)
(2)写出一个不确定事件.(只需写一个,填在下面的横线上)
18.从一副普通的扑克牌中取出五张牌,它们的牌面数字分别是4,4,5,5,6.
(1)将这五张扑克牌背面朝上,洗匀后从中随机抽取一张,则抽取的这张牌的牌面数字是4的概率是多少?
(2)将这五张扑克牌背面明上,洗匀后从中随机抽取一张(不放回),再从中随机抽取第二张,请用列表或画树状图的方法,求抽取的这两张牌的牌面数字之和为奇数的概率.
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 b 295 480 601
摸到白球的频率 a 0.64 0.59 0.59 0.60 0.601
(1)上表中的a= ,b= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)如果袋中有15个白球,那么袋中除了白球外,还有多少个其它颜色的球.
20.口袋里只有8个球,除颜色外都相同,其中有x个红球,y个白球,没有其他颜色的球,从中随意摸出一个球:(1)如果摸到红球与摸到白球的可能性相等,分别求x和y的值.
(2)在(1)的条件下,现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是,求取走多少个白球.
21.一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率;
(2)先从中任意摸出1个球,再从余下的2个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
22.工厂质检员对甲员工近期生产的产品进行抽检,统计合格的件数,得到如下表格:
抽取件数(件) 50 100 200 300 500 1000
合格频数 49 94 192 285 m 950
合格频率 0.98 0.94 0.96 0.95 0.95 n
(1)表格中m的值为 ,n的值为 .
(2)估计任抽一件该产品是不合格品的概率.
(3)该工厂规定,若每被抽检出一件不合格产品,需在相应员工奖金中扣除给工厂2元的材料损失费,今天甲员工被抽检了460件产品,估计要在他奖金中扣除多少材料损失费?
23.在学习概率的课堂上,老师提出问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
24.为了解班级学生参加课后服务的学习效果,何老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)此次调查的总人数为 ;
(2)扇形统计图中“不达标”对应的圆心角度数是 °;
(3)请将条形统计图补充完整;
(4)为了共同进步,何老师准备从被调查的A类和D类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列事件为随机事件的是( )
A.负数大于正数 B.三角形内角和等于180°C.明天太阳从东方升起 D.购买一张彩票,中奖
【点拨】根据已知条件,结合必然事件、随机事件、随机事件的定义即可求解.
【解析】解:A.负数大于正数是不可能事件,不符合题意;
B.三角形内角和等于180°是必然事件,不符合题意;
C.明天太阳从东方升起是必然事件,不符合题意;
D.购买一张彩票,中奖是随机事件,符合题意.
故选:D.
【点睛】本题主要考查必然事件、随机事件、随机事件的定义,属于基础题,理解相关概念是关键.
2.盒子里有10个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大 C.不可能是黑球 D.摸出黄球的可能性最小
【点拨】根据题意列出树状图求出各种颜色求得概率,逐个判断即可得到答案.
【解析】解:由题意可得,
摸出红球的概率为,摸出黄球的概率为:,摸出黑球的概率为:,
故选:B.
【点睛】本题考查概率定义及树状图法求概率,解题的关键是正确理解概率的定义.
3.在一个不透明的袋子中装有3个红球,2个白球和4个黄球.每个球除颜色外其余均相同,从袋中随机摸出一个球,摸到红球的概率是( )
A. B. C. D.
【点拨】根据概率的公式计算即可.
【解析】解:.
故选:B.
【点睛】本题主要考查了概率的公式,熟知:如果一个事件有n种可能,而且这些事件发生的可能性相同,其中事件A出现m种结果,那么事件A的概率为:.
4.如图,一只松鼠先经过第一道门(A,B或C),再经过第二道门(D或E)出去,则松鼠走出笼子的路线是“先经过A门,再经过E门”的概率是( )
A. B. C. D.
【点拨】画树状图列出所有等可能结果,从中找到松鼠走出笼子的路线是“先经过A门,再经过E门”的结果数,再根据概率公式求解即可.
【解析】解:画树状图如下:
共有6种等可能的结果,其中松鼠走出笼子的路线是“先经过A门,再经过E门”的只有1种结果,
所以松鼠走出笼子的路线是“先经过A门,再经过E门”的概率为,
故选:D.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
5.从长度为1cm,1cm,2cm,2cm的4条线段中任意选3条线段,这三条线段能够组成等腰三角形的概率是( )
A. B. C. D.
【点拨】利用完全列举法展示所有4种等可能的结果,然后根据等腰三角形的判定方法和概率公式求解.
【解析】解:从4条线段中任意选3条线段的所有结果为1、1、2;1、1、2;1、2、2;1、2、2,共有4种等可能的结果,
其中这三条线段能够组成等腰三角形的结果数为2种,
所有这三条线段能够组成等腰三角形的概率==.
故选:A.
【点睛】本题考查了列表法与树状图法:利用完全列举法展示所有可能的结果.也考查了三角形三边的关系和等腰三角形的判定.
6.我国自古以来就有植树的传统,植树可以净化沙土,防止土地沙漠化,对于调节气候、涵养水源、减轻大气污染具有重要意义.在清明时节植树为最佳,因为此时的气候温暖,适宜树苗的成活.某林业局将一种树苗移植成活的情况绘制成如图统计图,由此可估计这种树苗移植成活的概率约为( )
A.0.80 B.0.85 C.0.90 D.0.95
【点拨】由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9.
【解析】解:这种树苗成活的频率稳定在0.9,成活的概率估计值约是0.90.
故选:C.
【点睛】本题考查了利用频率估计概率.由于树苗数量巨大,故其成活的概率与频率可认为近似相等.用到的知识点为:总体数目=部分数目÷相应频率.部分的具体数目=总体数目×相应频率.
7.以下说法合理的是( )
A.小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
B.某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C.某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
D.小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
【点拨】根据各个选项中的说法可以判断是否正确,从而可以解答本题.
【解析】解:小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是是错误的,3次试验不能总结出概率,故选项A错误,
某彩票的中奖概率是5%,那么买100张彩票可能有5张中奖,但不一定有5张中奖,故选项B错误,
某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是不正确,中靶与不中靶不是等可能事件,故选项C错误,
小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的可能性是,故选项D正确,
故选:D.
【点睛】本题考查利用频率估计概率,解答本题的关键是明确题意,可以判断各个选项中的说法是否正确.
8.如图所示,有一电路连着三个开关,每个开关闭合的可能性均为,若不考虑元件的故障因素,则电灯点亮的可能性为( )
A. B. C. D.
【点拨】用列举法列举出可能出现的情况,在根据概率公式求解即可.
【解析】解:由于每个开关闭合的可能性均为,则共有8种情况;
1、K1关、K2关、K3开;
2、K1关、K2关、K3关;
3、K1关、K2开、K3开;
4、K1关、K2开、K3关;
5、K1开、K2开、关K3;
6、K1开、K2关、K3关;
7、K1开、K2开、K3开;
8、K1开、K2开、K3关.
只有5、7、8电灯可点亮,可能性为.
故选:C.
【点睛】本题考查的是可能性大小的判断,用到的知识点为:可能性等于所求情况数与总情况数之比.
9.袋中有除颜色以外其余都相同的红球3个,黄球1个.从中任意摸出1个球,记下颜色后放回、摇匀,像这样先后摸球2次,摸到的都是红球,则第3次摸到红球的概率是( )
A.1 B.O C. D.
【点拨】从中任意摸出1个球,有4种等可能结果,其中摸到红球的有3种结果,再根据概率公式求解即可.
【解析】解:从中任意摸出1个球,有4种等可能结果,其中摸到红球的有3种结果,
所以第3次摸到红球的概率是,
故选:C.
【点睛】本题主要考查概率公式,随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
10.一个密码箱的密码由五位数字组成,每个数位上的数都是从0到9的自然数.小明只记得其中的三个数字,则他一次就能打开锁的概率为( )
A. B. C. D.
【点拨】密码锁有五位数字组成,每一位数字都是0,1,2,3,4,5,6,7,8,9之中的一个,密码共100000种情况,小明只记得其中的三个数字,即有2个数字不准确共1000种情况;则他一次就能打开锁的概率为.
【解析】解:P(一次开锁)=.
故选:B.
【点睛】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率.
二、填空题:本题共6小题,每小题3分,共18分。
11.将一个正六面体骰子掷一次,它的点数恰好是4的概率是 .
【点拨】直接由概率公式求解即可.
【解析】解:∵掷一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子一次,它的点数恰好是4的情况有1种,
∴点数恰好是4的概率是,
故答案为:.
【点睛】本题考查了概率公式,熟记概率公式是解题的关键.
12.文明出行,遵守交通规则“红灯停,绿灯行”.已知一个十字路口的交通信号灯每分钟红灯亮20秒,绿灯亮30秒,黄灯亮10秒,则当圆圆经过这个路口时,信号灯恰好是绿灯的概率为 .
【点拨】直接利用概率公式可得答案.
【解析】解:经过这个路口信号灯是绿灯的概率是.
故答案为:.
【点睛】本题考查概率公式,熟练掌握概率公式是解答本题的关键.
13.一个袋子中有若干个白球和绿球,它们除了颜色外都相同.随机从中摸一个球,恰好摸到绿球的概率是,则袋子中至少有 3 个绿球.
【点拨】直接由概率公式即可得出结论.
【解析】解:∵一个袋子中有若干个白球和绿球,随机从中摸一个球,恰好摸到绿球的概率是,
∴袋子中至少有3个绿球,
故答案为:3.
【点睛】本题考查了概率公式:概率=所求情况数与总情况数之比.熟记概率公式是解题的关键.
14.在一个不透明的纸箱中装有4个白球和n个黄球,它们只有颜色不同.为了估计黄球的个数,杨老师进行了如下试验:每次从中随机摸出1个球,记下颜色后放回并摇匀.大量重复之后,杨老师发现摸到白球的频率稳定在附近,则n约为 8 .
【点拨】根据概率与频率的关系求解.
【解析】解:由题意得:=,
解得:n=8,
经检验:n=8是原分式方程的解,
故答案为:8.
【点睛】本题考查了利用频率估计概率,掌握频率与概率的关系是解题的关键.
15.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 .
【点拨】根据题意,可以画出相应的树状图,从而可以得到小乐抽到的两张邮票恰好是“立春”和“立夏”的概率.
【解析】解:设立春用A表示,立夏用B表示,秋分用C表示,大寒用D表示,画树状图如下,
由图可得,一共有12种等可能性的结果,
其中小乐抽到的两张邮票恰好是“立春”和“立夏”的可能性有2种,
∴小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是,
故答案为:.
【点睛】本题考查列表法与画树状图法求概率,解答本题的关键是明确题意,画出相应的树状图.
16.学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是 .
【点拨】画树状图,共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,然后由概率公式求解即可.
【解析】解:转盘B红色部分圆心角为240°,相当于2个蓝色部分,
画树状图如下:
共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,
∴小李同学同时转动A盘和B盘,她赢得游戏的概率是=.
【点睛】本题考查了树状图法求概率,正确画出树状图是解题的关键;用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1)下列事件中,哪些是必然事件?哪些是不可能事件?哪些是不确定事件?(填入题后括号内)
①校运会上,我班一位女同学的100米跑成绩是12秒11.( 不确定 事件)
②人在地球上所受的重力比在月球上小.( 不可能 事件)
③一个四边形四个内角的和等于360°.( 必然 事件)
(2)写出一个不确定事件.(只需写一个,填在下面的横线上) 明天会下雨(答案不唯一).
【点拨】根据事件发生的可能性大小判断即可.
【解析】解:(1)①校运会上,我班一位女同学的100米跑成绩是12秒11.(不确定事件)
②人在地球上所受的重力比在月球上小.(不可能事件)
③一个四边形四个内角的和等于360°.(必然事件)
(2)写出一个不确定事件.(只需写一个,填在下面的横线上) 明天会下雨(答案不唯一).
故答案为:(1)不确定,不可能,必然;(2)明天会下雨(答案不唯一).
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
18.从一副普通的扑克牌中取出五张牌,它们的牌面数字分别是4,4,5,5,6.
(1)将这五张扑克牌背面朝上,洗匀后从中随机抽取一张,则抽取的这张牌的牌面数字是4的概率是多少?
(2)将这五张扑克牌背面明上,洗匀后从中随机抽取一张(不放回),再从中随机抽取第二张,请用列表或画树状图的方法,求抽取的这两张牌的牌面数字之和为奇数的概率.
【点拨】(1)找出五张牌中,牌面数字为4的张数,求出抽取的这张牌的牌面数字是4的概率即可;
(2)列表得出所有等可能的情况数,找出抽取的这两张牌的牌面数字之和为奇数的情况数,即可求出所求.
【解析】解:(1)五张牌中,牌面数字分别是4,4,5,5,6,其中牌面数字为4的张数为2,
则P(牌面数字为4)=;
(2)列表如下:
4 4 5 5 6
4 ﹣﹣﹣ 8 9 9 10
4 8 ﹣﹣﹣ 9 9 10
5 9 9 ﹣﹣﹣ 10 11
5 9 9 10 ﹣﹣﹣ 11
6 10 10 11 11 ﹣﹣﹣
所有等可能的情况有20种,其中抽取的这两张牌的牌面数字之和为奇数的情况有12种,
则P(抽取的这两张牌的牌面数字之和为奇数)==.
【点睛】此题考查了列表法与树状图法,以及概率公式,用到的知识为:概率=所求情况数与总情况数之比.
19.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 b 295 480 601
摸到白球的频率 a 0.64 0.59 0.59 0.60 0.601
(1)上表中的a= 0.58 ,b= 118 ;
(2)“摸到白球”的概率的估计值是 0.6 (精确到0.1);
(3)如果袋中有15个白球,那么袋中除了白球外,还有多少个其它颜色的球.
【点拨】(1)利用频率=频数÷样本容量直接求解即可;
(2)根据统计数据,当n很大时,摸到白球的频率接近0.6;
(3)根据利用频率估计概率,可估计摸到白球的概率为0.6,然后利用概率公式计算其它颜色的球的个数.
【解析】解:(1)a=58÷100=0.58,b=200×0.59=118,
故答案为:0.58,118;
(2)由表格的数据可得,
“摸到白球的”的概率的估计值是0.6.
故答案为:0.6;
(3)15÷0.6﹣15=10(个),
答:除白球外,还有大约10个其它颜色的小球.
【点睛】本题考查了利用频率估计概率:大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
20.口袋里只有8个球,除颜色外都相同,其中有x个红球,y个白球,没有其他颜色的球,从中随意摸出一个球:(1)如果摸到红球与摸到白球的可能性相等,分别求x和y的值.
(2)在(1)的条件下,现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是,求取走多少个白球.
【点拨】(1)根据红球与白球的数量的情况即可求解;
(2)设取走x个白球,根据概率公式列出关于x的方程,解出x的值即可.
【解析】解:(1)∵摸到红球与摸到白球的可能性相等,且x+y=8,
∴x=y=4;
(2)设取走x个白球,放入x个红球,则口袋中现在有白球(4﹣x)个,红球(4+x)个,
根据题意得,=,
解得x=3,
答:取走3个白球.
【点睛】本题主要考查概率公式,随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
21.一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率;
(2)先从中任意摸出1个球,再从余下的2个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
【点拨】(1)直接利用概率公式求解;
(2)画树状图展示所有6种等可能的结果数,找出两次都摸到红球的结果数,然后根据概率公式求解.
【解析】解:(1)搅匀后从中任意摸出1个球,摸到红球的概率=;
故答案为:;
(2)画树状图为:
共有6种等可能的结果数,其中两次都摸到红球的结果数为2,
所以两次都摸到红球的概率==.
【点睛】此题考查列表法与树状图法,概率公式,解答本题的关键要熟练掌握概率的求法:概率=所求情况数与总情况数之比.
22.工厂质检员对甲员工近期生产的产品进行抽检,统计合格的件数,得到如下表格:
抽取件数(件) 50 100 200 300 500 1000
合格频数 49 94 192 285 m 950
合格频率 0.98 0.94 0.96 0.95 0.95 n
(1)表格中m的值为 475 ,n的值为 0.95 .
(2)估计任抽一件该产品是不合格品的概率.
(3)该工厂规定,若每被抽检出一件不合格产品,需在相应员工奖金中扣除给工厂2元的材料损失费,今天甲员工被抽检了460件产品,估计要在他奖金中扣除多少材料损失费?
【点拨】(1)根据频率=频数÷总数求解即可;
(2)用1减去合格品频率的稳定值即可;
(3)总数量乘以不合格品的概率,再乘以每件的损失费即可.
【解析】解:(1)m=500×0.95=475,n=950÷1000=0.95,
故答案为:475、0.95;
(2)1﹣0.95=0.05.
答:任抽一件该产品是不合格品的概率为0.05;
(3)460×0.05×2=46(元).
答:估计要在他奖金中扣除46元.
【点睛】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
23.在学习概率的课堂上,老师提出问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
【点拨】(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,比较即可.
(2)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率,比较即可.
【解析】解:(1)甲同学的方案不公平.理由如下:
列表法,
小丽小芳 2 3 4 5
2 (2,3) (2,4) (2,5)
3 (3,2) (3,4) (3,5)
4 (4,2) (4,3) (4,5)
5 (5,2) (5,3) (5,4)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有8种,故小丽获胜的概率为:=,则小芳获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
(2)公平.理由如下:
列表如下:
小丽小芳 2 3 5 7
2 (2,3) (2,5) (2,7)
3 (3,2) (3,5) (3,7)
5 (5,2) (5,3) (5,7)
7 (7,2) (7,3) (7,5)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有:6种,故小丽获胜的概率为:=,则小芳获胜的概率为,
故此游戏两人获胜的概率相同,即他们的游戏规则公平.
【点睛】此题主要考查了游戏公平性,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合于两步或两步以上的完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
24.为了解班级学生参加课后服务的学习效果,何老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)此次调查的总人数为 20 ;
(2)扇形统计图中“不达标”对应的圆心角度数是 36 °;
(3)请将条形统计图补充完整;
(4)为了共同进步,何老师准备从被调查的A类和D类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.
【点拨】(1)根据A等级的人数和所占的百分比即可得出答案;
(2)用360°乘以“不达标”所占的百分比即可得出答案;
(3)先求出C等级的女生和D等级的男生,然后补全统计图即可;
(4)根据题意画出树状图得出所有等可能的情况数,找出符合条件的情况数,然后根据概率公式即可得出答案.
【解析】解:(1)调查的总人数为:3÷15%=20(人),
故答案为:20;
(2)360°×(1﹣50%﹣25%﹣15%)=36°,
答:扇形统计图中“课前预习不达标”对应的圆心角度数是36°;
故答案为:36;
(3)C等级的人数有:20×25%=5(人),
C等级的女生人数有:5﹣2=3(人),
D等级的男生人数有:20﹣(1+2+6+4+5+1)=1(人),
补全统计图如下:
(4)由题意画树形图如下:
从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选两位同学恰好是一位男同学和一位女同学的结果共有3种.
所以P(所选两位同学恰好是一位男同学和一位女同学)==.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
