第1章 三角形的初步知识(含答案)2024-2025学年数学浙教版八年级上册
文档属性
| 名称 | 第1章 三角形的初步知识(含答案)2024-2025学年数学浙教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 383.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 19:51:39 | ||
图片预览


文档简介
第1章三角形的初步知识
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列长度的三条线段,能组成三角形的是( )
A. 3,4,7 B. 5,6,10 C. 2,3,6 D. 5,6,11
2.在一个三角形中,若三个内角度数之比为,则这个三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 无法确定
3.如图,BE是某个三角形的高线,则这个三角形是( )
A. B. C. D.
4.下列命题中是假命题的是( )
A. 两直线平行,同旁内角互补 B. 同位角相等,两直线平行
C. 若,,那么 D. 相等的角是对顶角
5.如图,已知≌,,,,则AC的长为( )
A. 3 B. 7 C. 9 D. 无法确定
6.如图,在中,D在BC的延长线上,E在CA的延长线上,F在AB上,与的大小关系是( )
A. B. C. D. 不确定
7.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是( )
A. ① B. ② C. ③ D. ④
8.如图,AD是的中线,CE是的中线,DF是的中线,如果的面积是2,那么的面积为( )
A. 12 B. 14 C. 16 D. 18
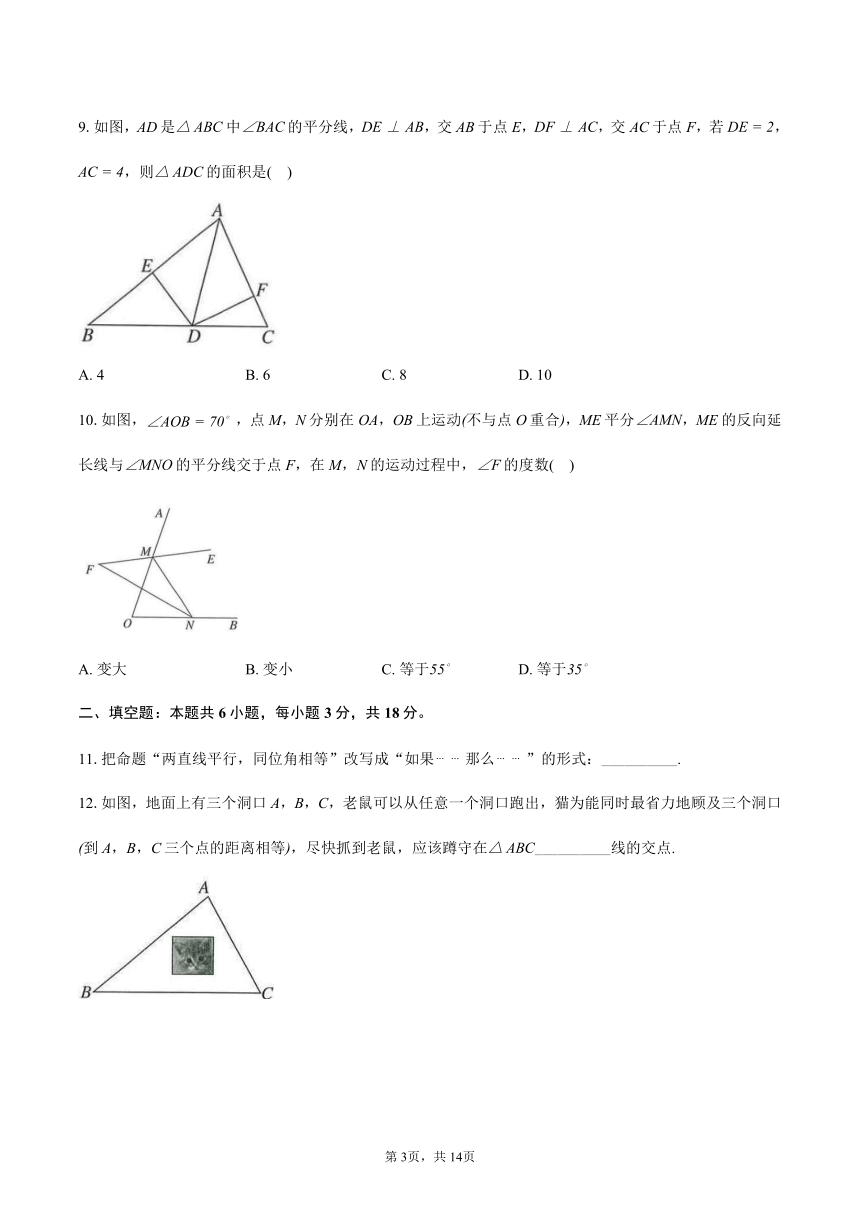
9.如图,AD是中的平分线,,交AB于点E,,交AC于点F,若,,则的面积是( )
A. 4 B. 6 C. 8 D. 10
10.如图,,点M,N分别在OA,OB上运动不与点O重合,ME平分,ME的反向延长线与的平分线交于点F,在M,N的运动过程中,的度数( )
A. 变大 B. 变小 C. 等于 D. 等于
二、填空题:本题共6小题,每小题3分,共18分。
11.把命题“两直线平行,同位角相等”改写成“如果那么”的形式:__________.
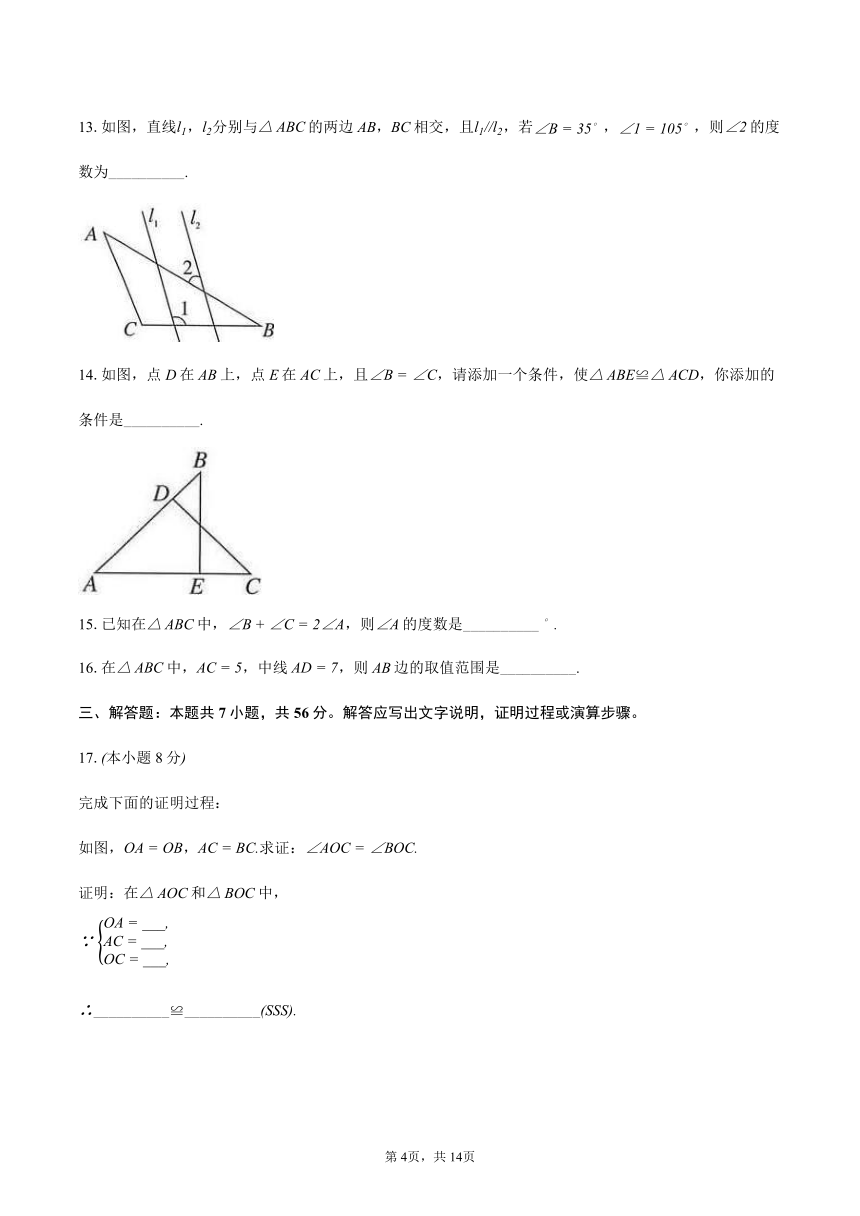
12.如图,地面上有三个洞口A,B,C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及三个洞口到A,B,C三个点的距离相等,尽快抓到老鼠,应该蹲守在__________线的交点.
13.如图,直线,分别与的两边AB,BC相交,且,若,,则的度数为__________.
14.如图,点D在AB上,点E在AC上,且,请添加一个条件,使≌,你添加的条件是__________.
15.已知在中,,则的度数是__________
16.在中,,中线,则AB边的取值范围是__________.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
完成下面的证明过程:
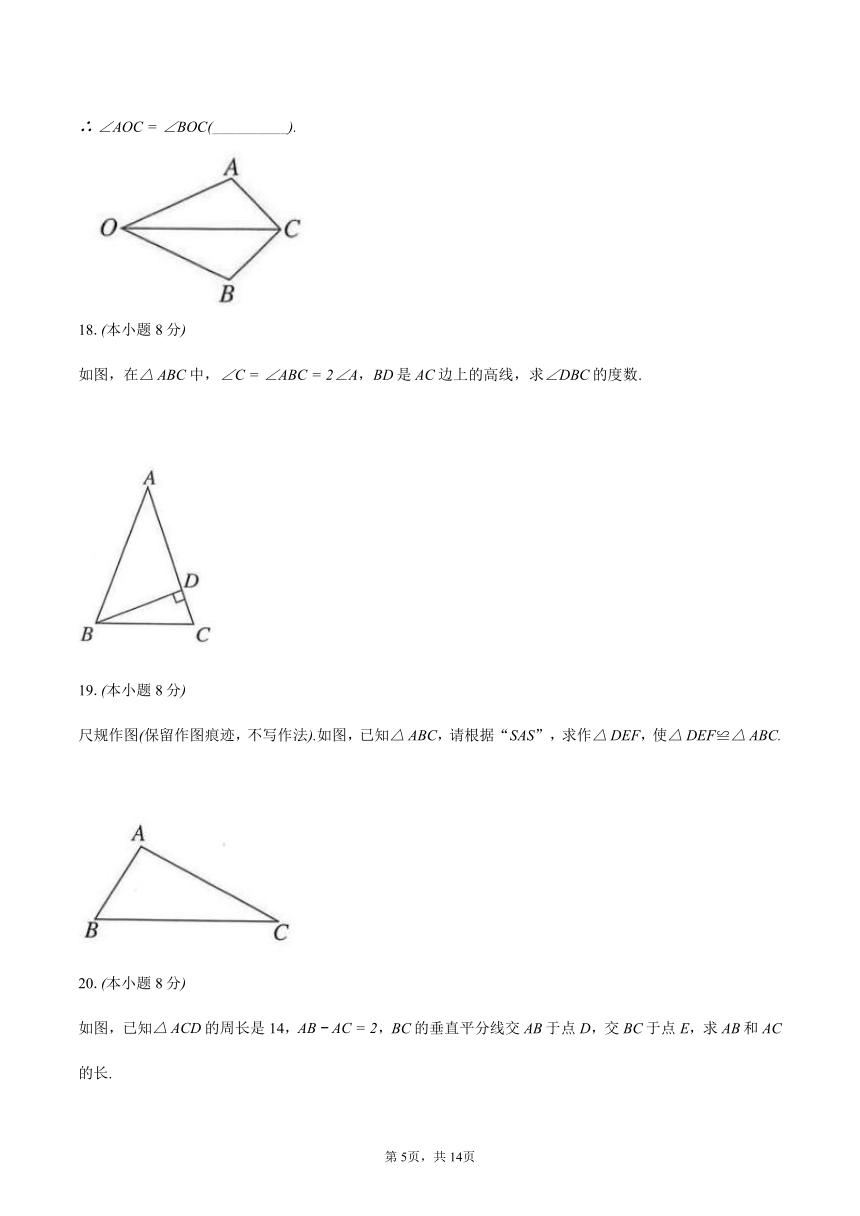
如图,,求证:
证明:在和中,
__________≌__________
__________
18.本小题8分
如图,在中,,BD是AC边上的高线,求的度数.
19.本小题8分
尺规作图保留作图痕迹,不写作法如图,已知,请根据“SAS”,求作,使≌
20.本小题8分
如图,已知的周长是14,,BC的垂直平分线交AB于点D,交BC于点E,求AB和AC的长.
21.本小题8分
在中,AE是的高线.
如图1,若AD是的平分线,,,请说明的度数.
如图2,延长AC到点F,和的平分线交于点G,求的度数.
22.本小题8分
如图,已知,OM是的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,
和PD的数量关系是__________.
请证明中得出的结论.
23.本小题8分
“面积法”是指利用图形面积间的等量关系寻求线段间等量关系的一种方法.
在中,,点P是射线BC上一个动点,过点P作,,垂足分别为点D,E,BF为边AC上的高线,试探究BF,PD,PE之间的数量关系,并说明理由.
如图,P是等边三角形ABC内部一点,作,,,垂足分别为点D,E,F,若,,,求的高.
答案和解析
1.【答案】B
【解析】略
2.【答案】B
【解析】略
3.【答案】A
【解析】略
4.【答案】D
【解析】略
5.【答案】B
【解析】略
6.【答案】A
【解析】略
7.【答案】C
【解析】略
8.【答案】C
【解析】略
9.【答案】A
【解析】略
10.【答案】D
【解析】平分,NF平分,
,
又是的外角,
,
即,
又是的外角,
,
,
11.【答案】如果两直线平行,那么同位角相等
【解析】略
12.【答案】三边垂直平分
【解析】略
13.【答案】
【解析】略
14.【答案】答案不唯一
【解析】略
15.【答案】60
【解析】略
16.【答案】
【解析】略
17.【答案】证明:在和中,
≌
全等三角形的对应角相等
【解析】见答案
18.【答案】解:设,则,由三角形内角和为,
得,
,解得,
是AC边上的高线,,
【解析】见答案
19.【答案】如图,为所作.
【解析】见答案
20.【答案】的垂直平分线交AB于点D,
的周长是14,
,即,
则
,
【解析】见答案
21.【答案】【小题1】
,,
是的平分线,
是BC边上的高线,
在中,,
【小题2】
设,
,
,
和的平分线交于点G,
,
,
【解析】见答案
见答案
22.【答案】【小题1】
【小题2】
证明:如图,过点P分别作于点E,于点F,
是的平分线,
,
,
,
,
在和中,
≌,
【解析】略
见答案
23.【答案】【小题1】
如图1,当点P在边BC上时,连结
,
,
,
如图2,当点P在边BC的延长线上时,连结
,
,
,
【小题2】
如图3,过A作于H,连结PA,PB,PC,
,
是等边三角形,
,
【解析】见答案
见答案
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列长度的三条线段,能组成三角形的是( )
A. 3,4,7 B. 5,6,10 C. 2,3,6 D. 5,6,11
2.在一个三角形中,若三个内角度数之比为,则这个三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 无法确定
3.如图,BE是某个三角形的高线,则这个三角形是( )
A. B. C. D.
4.下列命题中是假命题的是( )
A. 两直线平行,同旁内角互补 B. 同位角相等,两直线平行
C. 若,,那么 D. 相等的角是对顶角
5.如图,已知≌,,,,则AC的长为( )
A. 3 B. 7 C. 9 D. 无法确定
6.如图,在中,D在BC的延长线上,E在CA的延长线上,F在AB上,与的大小关系是( )
A. B. C. D. 不确定
7.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是( )
A. ① B. ② C. ③ D. ④
8.如图,AD是的中线,CE是的中线,DF是的中线,如果的面积是2,那么的面积为( )
A. 12 B. 14 C. 16 D. 18
9.如图,AD是中的平分线,,交AB于点E,,交AC于点F,若,,则的面积是( )
A. 4 B. 6 C. 8 D. 10
10.如图,,点M,N分别在OA,OB上运动不与点O重合,ME平分,ME的反向延长线与的平分线交于点F,在M,N的运动过程中,的度数( )
A. 变大 B. 变小 C. 等于 D. 等于
二、填空题:本题共6小题,每小题3分,共18分。
11.把命题“两直线平行,同位角相等”改写成“如果那么”的形式:__________.
12.如图,地面上有三个洞口A,B,C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及三个洞口到A,B,C三个点的距离相等,尽快抓到老鼠,应该蹲守在__________线的交点.
13.如图,直线,分别与的两边AB,BC相交,且,若,,则的度数为__________.
14.如图,点D在AB上,点E在AC上,且,请添加一个条件,使≌,你添加的条件是__________.
15.已知在中,,则的度数是__________
16.在中,,中线,则AB边的取值范围是__________.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
完成下面的证明过程:
如图,,求证:
证明:在和中,
__________≌__________
__________
18.本小题8分
如图,在中,,BD是AC边上的高线,求的度数.
19.本小题8分
尺规作图保留作图痕迹,不写作法如图,已知,请根据“SAS”,求作,使≌
20.本小题8分
如图,已知的周长是14,,BC的垂直平分线交AB于点D,交BC于点E,求AB和AC的长.
21.本小题8分
在中,AE是的高线.
如图1,若AD是的平分线,,,请说明的度数.
如图2,延长AC到点F,和的平分线交于点G,求的度数.
22.本小题8分
如图,已知,OM是的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,
和PD的数量关系是__________.
请证明中得出的结论.
23.本小题8分
“面积法”是指利用图形面积间的等量关系寻求线段间等量关系的一种方法.
在中,,点P是射线BC上一个动点,过点P作,,垂足分别为点D,E,BF为边AC上的高线,试探究BF,PD,PE之间的数量关系,并说明理由.
如图,P是等边三角形ABC内部一点,作,,,垂足分别为点D,E,F,若,,,求的高.
答案和解析
1.【答案】B
【解析】略
2.【答案】B
【解析】略
3.【答案】A
【解析】略
4.【答案】D
【解析】略
5.【答案】B
【解析】略
6.【答案】A
【解析】略
7.【答案】C
【解析】略
8.【答案】C
【解析】略
9.【答案】A
【解析】略
10.【答案】D
【解析】平分,NF平分,
,
又是的外角,
,
即,
又是的外角,
,
,
11.【答案】如果两直线平行,那么同位角相等
【解析】略
12.【答案】三边垂直平分
【解析】略
13.【答案】
【解析】略
14.【答案】答案不唯一
【解析】略
15.【答案】60
【解析】略
16.【答案】
【解析】略
17.【答案】证明:在和中,
≌
全等三角形的对应角相等
【解析】见答案
18.【答案】解:设,则,由三角形内角和为,
得,
,解得,
是AC边上的高线,,
【解析】见答案
19.【答案】如图,为所作.
【解析】见答案
20.【答案】的垂直平分线交AB于点D,
的周长是14,
,即,
则
,
【解析】见答案
21.【答案】【小题1】
,,
是的平分线,
是BC边上的高线,
在中,,
【小题2】
设,
,
,
和的平分线交于点G,
,
,
【解析】见答案
见答案
22.【答案】【小题1】
【小题2】
证明:如图,过点P分别作于点E,于点F,
是的平分线,
,
,
,
,
在和中,
≌,
【解析】略
见答案
23.【答案】【小题1】
如图1,当点P在边BC上时,连结
,
,
,
如图2,当点P在边BC的延长线上时,连结
,
,
,
【小题2】
如图3,过A作于H,连结PA,PB,PC,
,
是等边三角形,
,
【解析】见答案
见答案
第1页,共1页
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
