第5章 一次函数 单元练习(含答案)2024-2025学年数学浙教版八年级上册
文档属性
| 名称 | 第5章 一次函数 单元练习(含答案)2024-2025学年数学浙教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 218.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 20:03:21 | ||
图片预览


文档简介
第5章一次函数
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在长方形周长计算公式中长方形的长为a,宽为b,周长为,对长和宽不同的长方形,变量是( )
A. C B. a,b C. C,a,b D. C,
2.如图,直线经过点,则不等式的解为( )
A. B. C. D.
3.若直线与坐标轴围成的三角形的面积为S,则S等于( )
A. 2 B. 4 C. 6 D. 8
4.已知将直线向上平移2个单位后得到直线,则下列关于直线的说法,正确的是( )
A. 经过第一、二、四象限 B. 与x轴相交于点
C. 与y轴相交于点 D. y随x的增大而减小
5.已知一次函数,y随x的增大而减小,且图象与y轴的交点在x轴上方,则实数m的取值范围是( )
A. B.
C. 或 D.
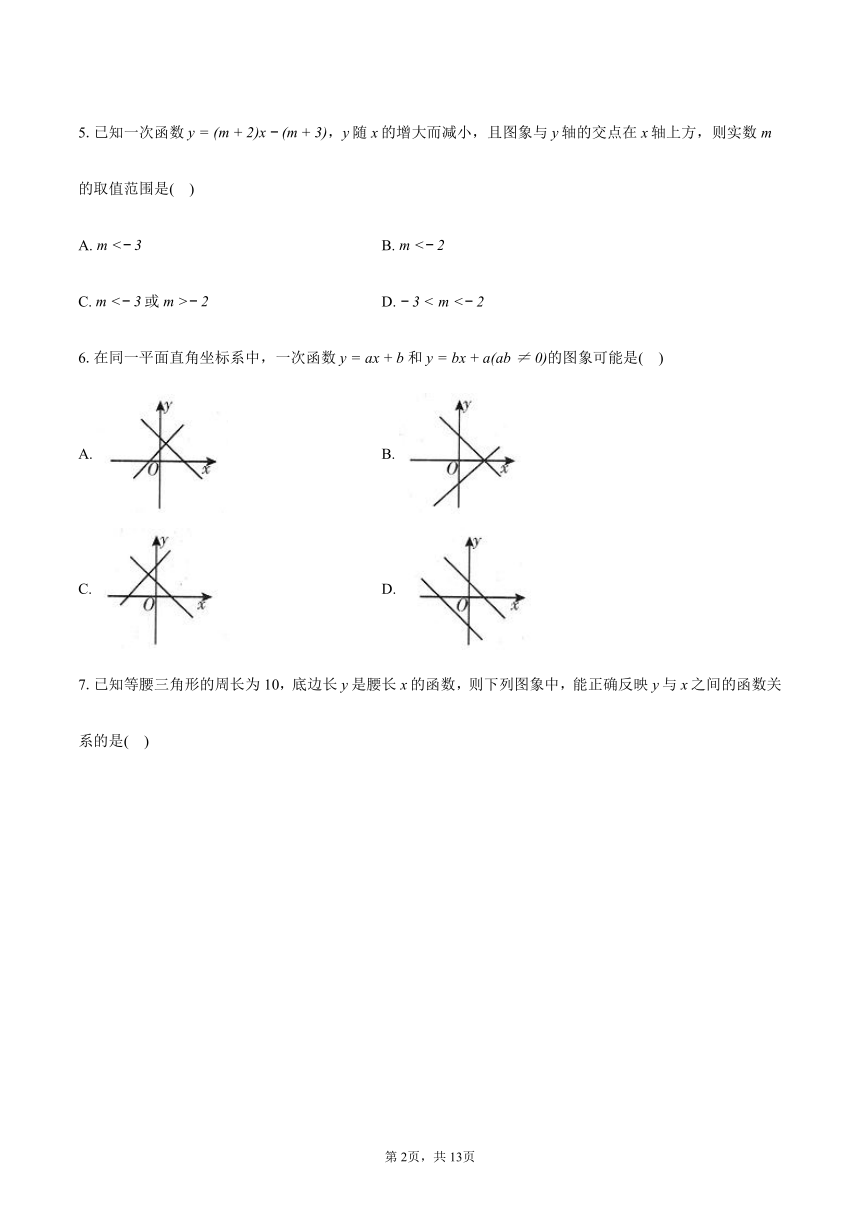
6.在同一平面直角坐标系中,一次函数和的图象可能是( )
A. B.
C. D.
7.已知等腰三角形的周长为10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间的函数关系的是( )
A. B.
C. D.
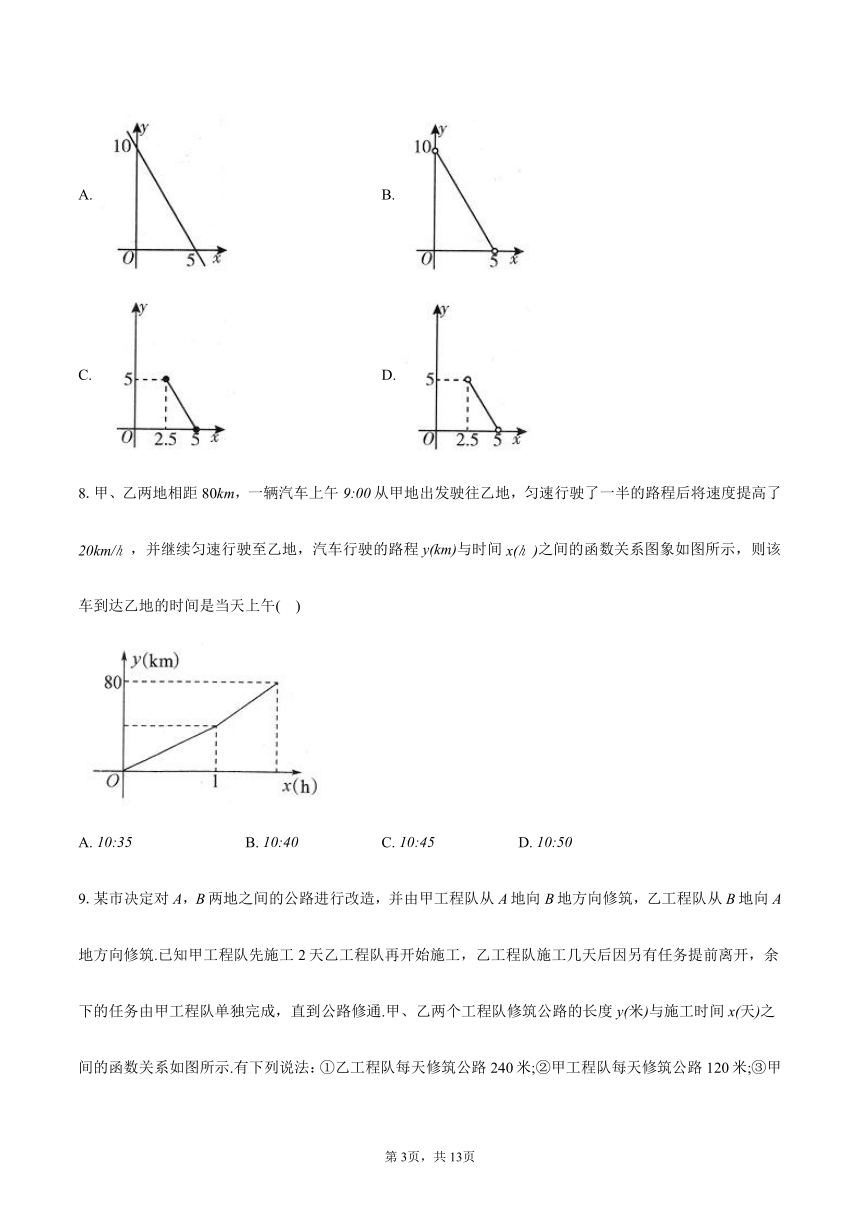
8.甲、乙两地相距80km,一辆汽车上午从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了,并继续匀速行驶至乙地,汽车行驶的路程与时间之间的函数关系图象如图所示,则该车到达乙地的时间是当天上午( )
A. B. C. D.
9.某市决定对A,B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修筑公路的长度米与施工时间天之间的函数关系如图所示.有下列说法:①乙工程队每天修筑公路240米;②甲工程队每天修筑公路120米;③甲工程队比乙工程队多工作6天;④,B两地之间的公路总长为1680米.其中正确的是( )
A. ①④ B. ①②③ C. ②③④ D. ①②③④
10.已知,,为直线上的三个点,且,则下列判断中,正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
二、填空题:本题共6小题,每小题3分,共18分。
11.若是一次函数,则m的值为__________.
12.已知点,在直线上,且直线经过第一、二、四象限,当时,__________填“>”“<”或“=”
13.如图,直线过,两点,则的解为__________.
14.函数与的图象的交点在x轴上,则__________.
15.若点关于y轴的对称点位于第四象限,则一次函数的图象不经过第__________象限.
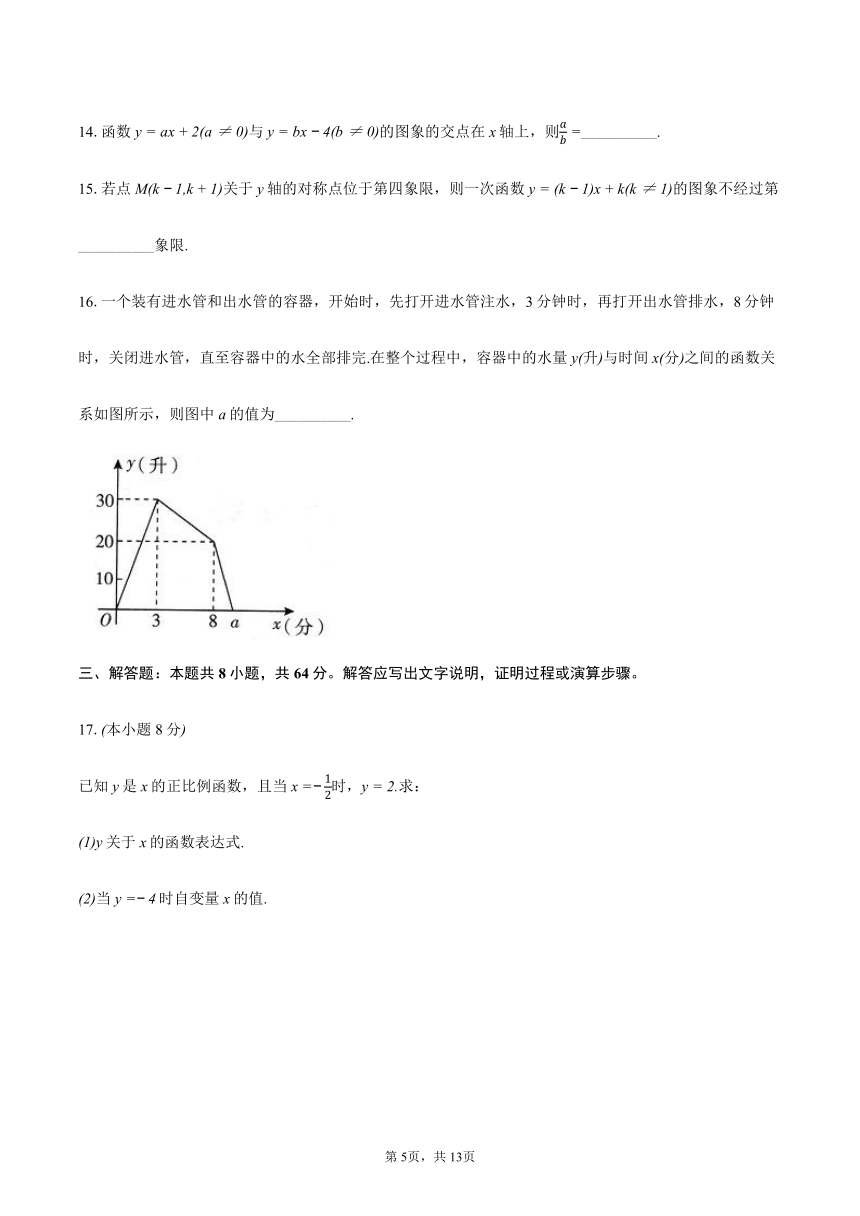
16.一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量升与时间分之间的函数关系如图所示,则图中a的值为__________.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
已知y是x的正比例函数,且当时,求:
关于x的函数表达式.
当时自变量x的值.
18.本小题8分
如图,直线与x轴相交于点A,与y轴相交于点
求A,B两点的坐标.
过点A作直线AP与y轴相交于点P,且使,求直线AP的函数表达式.
19.本小题8分
已知一次函数的图象过点,且与两坐标轴围成的三角形的面积为2,求此一次函数的表达式.
20.本小题8分
按要求完成作图并答题:
作出关于y轴对称的
求的面积.
在y轴上找一点P,使得的周长最小,在图中找到点P并求出点P的坐标.
21.本小题8分
如图,在平面直角坐标系中,点A,B的坐标分别为,,连结AB,以AB为边向上作等边三角形求:
点C的坐标.
线段BC所在直线的函数表达式.
22.本小题8分
某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A种菜苗的价格是菜苗基地的倍,用300元在市场上购买的A种菜苗比在菜苗基地购买的少3捆.
求菜苗基地每捆A种菜苗的价格.
菜苗基地每捆B种菜苗的价格是30元.学校决定在菜苗基地购买A,B两种菜苗共100捆,且A种菜苗的捆数不超过B种菜苗的捆数.菜苗基地为支持该校活动,对A,B两种菜苗均提供九折优惠.求本次购买最少花费多少钱.
23.本小题8分
A,B两地相距290千米,早上甲货车从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系地收到消息后立即派乙货车从B地出发去接运甲货车上的物资,乙货车遇到甲货车后,用了30分钟将物资从甲货车搬运到乙货车上,随后开往B地,两辆货车离开各自出发地的路程千米与甲出发的时间时的函数关系如图所示.
直接写出甲货车,乙货车相遇前的速度.
求乙货车在未遇到甲货车时,它离开出发地的路程千米关于甲出发的时间时的函数表达式.
因实际需要,要求乙货车到达B地的时间比甲货车按原来的速度正常到达B地的时间最多晚1个小时,问乙货车返回B地的速度至少为多少
24.本小题8分
操作思考:如图1,在平面直角坐标系中,等腰直角三角形ACB的直角顶点C在原点O处,将其绕着点O旋转,若顶点A恰好落在点处,则OA的长为__________;点B的坐标为__________.
感悟应用:如图2,在平面直角坐标系中,将等腰直角三角形ACB按如图所示的方式放置,直角顶点,点,试求直线AB的函数表达式.
拓展研究:如图3,在平面直角坐标系中,点,过点B作轴,垂足为A,轴,垂足为C,P是线段BC上的一个动点,Q是直线上的一个动点.问是否存在以点P为直角顶点的等腰直角三角形若存在,请求出此时点P的坐标;若不存在,请说明理由.
答案和解析
1.【答案】C
【解析】【分析】
本题考查变量,常量的定义.
根据变量的定义即可解答.
【解答】
解:,变量为a,b,常量:2
2.【答案】A
【解析】略
3.【答案】B
【解析】略
4.【答案】C
【解析】略
5.【答案】A
【解析】略
6.【答案】B
【解析】略
7.【答案】D
【解析】略
8.【答案】B
【解析】略
9.【答案】B
【解析】略
10.【答案】D
【解析】略
11.【答案】0
【解析】略
12.【答案】>
【解析】略
13.【答案】
【解析】略
14.【答案】
【解析】略
15.【答案】一
【解析】略
16.【答案】
【解析】略
17.【答案】
【解析】略
18.【答案】,
或
【解析】略
19.【答案】或
【解析】略
20.【答案】略
画图略,
【解析】略
21.【答案】
【解析】略
22.【答案】元
元
【解析】略
23.【答案】千米/时,100千米/时
千米/时
【解析】略
24.【答案】
存在或
【解析】略
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在长方形周长计算公式中长方形的长为a,宽为b,周长为,对长和宽不同的长方形,变量是( )
A. C B. a,b C. C,a,b D. C,
2.如图,直线经过点,则不等式的解为( )
A. B. C. D.
3.若直线与坐标轴围成的三角形的面积为S,则S等于( )
A. 2 B. 4 C. 6 D. 8
4.已知将直线向上平移2个单位后得到直线,则下列关于直线的说法,正确的是( )
A. 经过第一、二、四象限 B. 与x轴相交于点
C. 与y轴相交于点 D. y随x的增大而减小
5.已知一次函数,y随x的增大而减小,且图象与y轴的交点在x轴上方,则实数m的取值范围是( )
A. B.
C. 或 D.
6.在同一平面直角坐标系中,一次函数和的图象可能是( )
A. B.
C. D.
7.已知等腰三角形的周长为10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间的函数关系的是( )
A. B.
C. D.
8.甲、乙两地相距80km,一辆汽车上午从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了,并继续匀速行驶至乙地,汽车行驶的路程与时间之间的函数关系图象如图所示,则该车到达乙地的时间是当天上午( )
A. B. C. D.
9.某市决定对A,B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修筑公路的长度米与施工时间天之间的函数关系如图所示.有下列说法:①乙工程队每天修筑公路240米;②甲工程队每天修筑公路120米;③甲工程队比乙工程队多工作6天;④,B两地之间的公路总长为1680米.其中正确的是( )
A. ①④ B. ①②③ C. ②③④ D. ①②③④
10.已知,,为直线上的三个点,且,则下列判断中,正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
二、填空题:本题共6小题,每小题3分,共18分。
11.若是一次函数,则m的值为__________.
12.已知点,在直线上,且直线经过第一、二、四象限,当时,__________填“>”“<”或“=”
13.如图,直线过,两点,则的解为__________.
14.函数与的图象的交点在x轴上,则__________.
15.若点关于y轴的对称点位于第四象限,则一次函数的图象不经过第__________象限.
16.一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量升与时间分之间的函数关系如图所示,则图中a的值为__________.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
已知y是x的正比例函数,且当时,求:
关于x的函数表达式.
当时自变量x的值.
18.本小题8分
如图,直线与x轴相交于点A,与y轴相交于点
求A,B两点的坐标.
过点A作直线AP与y轴相交于点P,且使,求直线AP的函数表达式.
19.本小题8分
已知一次函数的图象过点,且与两坐标轴围成的三角形的面积为2,求此一次函数的表达式.
20.本小题8分
按要求完成作图并答题:
作出关于y轴对称的
求的面积.
在y轴上找一点P,使得的周长最小,在图中找到点P并求出点P的坐标.
21.本小题8分
如图,在平面直角坐标系中,点A,B的坐标分别为,,连结AB,以AB为边向上作等边三角形求:
点C的坐标.
线段BC所在直线的函数表达式.
22.本小题8分
某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A种菜苗的价格是菜苗基地的倍,用300元在市场上购买的A种菜苗比在菜苗基地购买的少3捆.
求菜苗基地每捆A种菜苗的价格.
菜苗基地每捆B种菜苗的价格是30元.学校决定在菜苗基地购买A,B两种菜苗共100捆,且A种菜苗的捆数不超过B种菜苗的捆数.菜苗基地为支持该校活动,对A,B两种菜苗均提供九折优惠.求本次购买最少花费多少钱.
23.本小题8分
A,B两地相距290千米,早上甲货车从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系地收到消息后立即派乙货车从B地出发去接运甲货车上的物资,乙货车遇到甲货车后,用了30分钟将物资从甲货车搬运到乙货车上,随后开往B地,两辆货车离开各自出发地的路程千米与甲出发的时间时的函数关系如图所示.
直接写出甲货车,乙货车相遇前的速度.
求乙货车在未遇到甲货车时,它离开出发地的路程千米关于甲出发的时间时的函数表达式.
因实际需要,要求乙货车到达B地的时间比甲货车按原来的速度正常到达B地的时间最多晚1个小时,问乙货车返回B地的速度至少为多少
24.本小题8分
操作思考:如图1,在平面直角坐标系中,等腰直角三角形ACB的直角顶点C在原点O处,将其绕着点O旋转,若顶点A恰好落在点处,则OA的长为__________;点B的坐标为__________.
感悟应用:如图2,在平面直角坐标系中,将等腰直角三角形ACB按如图所示的方式放置,直角顶点,点,试求直线AB的函数表达式.
拓展研究:如图3,在平面直角坐标系中,点,过点B作轴,垂足为A,轴,垂足为C,P是线段BC上的一个动点,Q是直线上的一个动点.问是否存在以点P为直角顶点的等腰直角三角形若存在,请求出此时点P的坐标;若不存在,请说明理由.
答案和解析
1.【答案】C
【解析】【分析】
本题考查变量,常量的定义.
根据变量的定义即可解答.
【解答】
解:,变量为a,b,常量:2
2.【答案】A
【解析】略
3.【答案】B
【解析】略
4.【答案】C
【解析】略
5.【答案】A
【解析】略
6.【答案】B
【解析】略
7.【答案】D
【解析】略
8.【答案】B
【解析】略
9.【答案】B
【解析】略
10.【答案】D
【解析】略
11.【答案】0
【解析】略
12.【答案】>
【解析】略
13.【答案】
【解析】略
14.【答案】
【解析】略
15.【答案】一
【解析】略
16.【答案】
【解析】略
17.【答案】
【解析】略
18.【答案】,
或
【解析】略
19.【答案】或
【解析】略
20.【答案】略
画图略,
【解析】略
21.【答案】
【解析】略
22.【答案】元
元
【解析】略
23.【答案】千米/时,100千米/时
千米/时
【解析】略
24.【答案】
存在或
【解析】略
第1页,共1页
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
