浙教版初三数学3.3垂径定理专题练习
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版初三数学3.3垂径定理专题练习
一、选择题
1.下列命题中正确的是( )
A.过三点一定可以作一个圆 B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.圆周角等于圆心角的一半 D.的圆周角所对的弦是直径
2.下列语句中,①过三点能作一个圆;②平分弦的直径垂直于弦;③长度相等的弧是等弧;④经过圆心的每一条直线都是圆的对称轴;⑤相等的圆心角所对的弧度数相等.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
3.下列命题中,正确的命题是( )
A.相等的圆心角所对的弧相等 B.平分弦的直径垂直于弦
C.经过三点一定可以作圆 D.三角形的外心到三角形三个顶点的距离相等
4.半径等于4的圆中,垂直平分半径的弦长为( )
A. B. C. D.
5.如图,两个同心圆的半径分别为和,弦与小圆相切于点,则( )
A. B. C. D.
6.如图,是的直径,点E在上,垂足为C,点G在上运动(不与E重合),点F为的中点,则的最大值为( )
A. B.6 C. D.8
7.如图,中,弦的长为,点在上,,.所在的平面内有一点,若,则点与的位置关系是( )
A.点在上 B.点在内 C.点在外 D.无法确定
8.如图,为的直径,弦于点,于点,若的半径为3,,则的长为( )
A.1 B. C. D.
9.⊙o的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.4
10.如图,⊙O的弦CD交直径AB于E,OD=DE,CE:DE=3:5,若OE=5,则CD的长为( )
A.4 B.4 C.3 D.3
11.如图,点E是的内心,的延长线和的外接圆相交于点D,与相交于点G,则下列结论:①;②若点G为的中点,则;③连接,若,则;④.其中一定正确的个数是( )
A.4 B.3 C.2 D.1
二、填空题
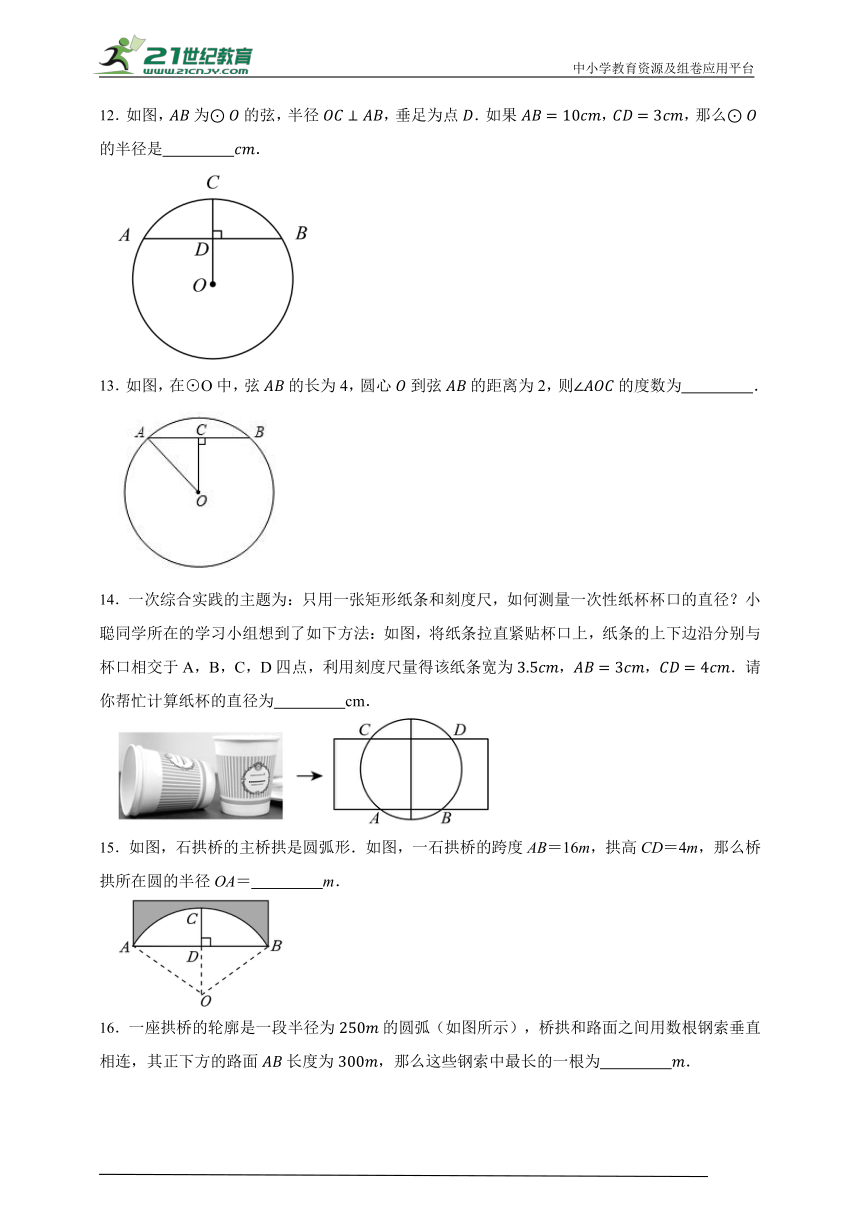
12.如图,为的弦,半径,垂足为点.如果,,那么的半径是 .
13.如图,在⊙O中,弦的长为4,圆心到弦的距离为2,则的度数为 .
14.一次综合实践的主题为:只用一张矩形纸条和刻度尺,如何测量一次性纸杯杯口的直径?小聪同学所在的学习小组想到了如下方法:如图,将纸条拉直紧贴杯口上,纸条的上下边沿分别与杯口相交于A,B,C,D四点,利用刻度尺量得该纸条宽为,,.请你帮忙计算纸杯的直径为 cm.
15.如图,石拱桥的主桥拱是圆弧形.如图,一石拱桥的跨度AB=16m,拱高CD=4m,那么桥拱所在圆的半径OA= m.
16.一座拱桥的轮廓是一段半径为的圆弧(如图所示),桥拱和路面之间用数根钢索垂直相连,其正下方的路面长度为,那么这些钢索中最长的一根为 .
17.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
18.如图,是的外接圆,于点,延长交于点,若,则的长是 .
19.⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为 .
三、解答题
20.石拱桥是我国古代人民勤劳和智慧的结晶(如图①),赵州桥是我国古代石拱桥的代表,图②是根据该石拱桥画出的几何图形,桥的主桥拱是圆弧形,表示为,桥的跨度(弧所对的弦长),设所在圆的圆心为O,,为半径,半径,垂足为D.拱高(弧的中点到弦的距离).
(1)直接写出与的数量关系;
(2)求这座石拱桥主桥拱的半径.
21.如图,AB是的直径,BC是弦,于点E,交于点D.
(1)请写出两个不同类型的正确结论;
(2)若,,求的半径.
22.如图所示,的直径为,弦,相交于点,已知点是的中点,弦的长为.
(1)求圆心到弦的距离.
(2)求的度数.
23.如图,,点,在射线上,以为直径作半圆,圆心为,半圆交射线于点,.
(1)如图1,当时,若,求的长;
(2)如图2,若,且,求的值.
24.如图,在中,弦、相交于点,连接,已知.
(1)求证:;
(2)如果的半径为,,,求的长.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】
13.【答案】
14.【答案】5
15.【答案】10
16.【答案】
17.【答案】
18.【答案】
19.【答案】3或1
20.【答案】(1)
(2)解:设主桥拱半径为,
∵,,,
∴,,
在中,由勾股定理,得,
即,
解得,
因此,这座石拱桥主桥拱半径约为.
21.【答案】(1)解:,.答案不唯一.
(2)解:∵,∴.
设的半径为r,则.
在Rt△OEB中,
由勾股定理,得,
即,解得,
∴的半径为5.
22.【答案】(1)2
(2)
23.【答案】(1)
(2)
24.【答案】(1)证明:∵,
,
在与中,,
≌,
;
(2)解:过作与,于,连接,,
根据垂径定理得:,,
,
,
在与中,
,
≌,
,
,
四边形是正方形,
,
设,
则,
,
即:,
解得:,舍去,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
浙教版初三数学3.3垂径定理专题练习
一、选择题
1.下列命题中正确的是( )
A.过三点一定可以作一个圆 B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.圆周角等于圆心角的一半 D.的圆周角所对的弦是直径
2.下列语句中,①过三点能作一个圆;②平分弦的直径垂直于弦;③长度相等的弧是等弧;④经过圆心的每一条直线都是圆的对称轴;⑤相等的圆心角所对的弧度数相等.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
3.下列命题中,正确的命题是( )
A.相等的圆心角所对的弧相等 B.平分弦的直径垂直于弦
C.经过三点一定可以作圆 D.三角形的外心到三角形三个顶点的距离相等
4.半径等于4的圆中,垂直平分半径的弦长为( )
A. B. C. D.
5.如图,两个同心圆的半径分别为和,弦与小圆相切于点,则( )
A. B. C. D.
6.如图,是的直径,点E在上,垂足为C,点G在上运动(不与E重合),点F为的中点,则的最大值为( )
A. B.6 C. D.8
7.如图,中,弦的长为,点在上,,.所在的平面内有一点,若,则点与的位置关系是( )
A.点在上 B.点在内 C.点在外 D.无法确定
8.如图,为的直径,弦于点,于点,若的半径为3,,则的长为( )
A.1 B. C. D.
9.⊙o的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.4
10.如图,⊙O的弦CD交直径AB于E,OD=DE,CE:DE=3:5,若OE=5,则CD的长为( )
A.4 B.4 C.3 D.3
11.如图,点E是的内心,的延长线和的外接圆相交于点D,与相交于点G,则下列结论:①;②若点G为的中点,则;③连接,若,则;④.其中一定正确的个数是( )
A.4 B.3 C.2 D.1
二、填空题
12.如图,为的弦,半径,垂足为点.如果,,那么的半径是 .
13.如图,在⊙O中,弦的长为4,圆心到弦的距离为2,则的度数为 .
14.一次综合实践的主题为:只用一张矩形纸条和刻度尺,如何测量一次性纸杯杯口的直径?小聪同学所在的学习小组想到了如下方法:如图,将纸条拉直紧贴杯口上,纸条的上下边沿分别与杯口相交于A,B,C,D四点,利用刻度尺量得该纸条宽为,,.请你帮忙计算纸杯的直径为 cm.
15.如图,石拱桥的主桥拱是圆弧形.如图,一石拱桥的跨度AB=16m,拱高CD=4m,那么桥拱所在圆的半径OA= m.
16.一座拱桥的轮廓是一段半径为的圆弧(如图所示),桥拱和路面之间用数根钢索垂直相连,其正下方的路面长度为,那么这些钢索中最长的一根为 .
17.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
18.如图,是的外接圆,于点,延长交于点,若,则的长是 .
19.⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为 .
三、解答题
20.石拱桥是我国古代人民勤劳和智慧的结晶(如图①),赵州桥是我国古代石拱桥的代表,图②是根据该石拱桥画出的几何图形,桥的主桥拱是圆弧形,表示为,桥的跨度(弧所对的弦长),设所在圆的圆心为O,,为半径,半径,垂足为D.拱高(弧的中点到弦的距离).
(1)直接写出与的数量关系;
(2)求这座石拱桥主桥拱的半径.
21.如图,AB是的直径,BC是弦,于点E,交于点D.
(1)请写出两个不同类型的正确结论;
(2)若,,求的半径.
22.如图所示,的直径为,弦,相交于点,已知点是的中点,弦的长为.
(1)求圆心到弦的距离.
(2)求的度数.
23.如图,,点,在射线上,以为直径作半圆,圆心为,半圆交射线于点,.
(1)如图1,当时,若,求的长;
(2)如图2,若,且,求的值.
24.如图,在中,弦、相交于点,连接,已知.
(1)求证:;
(2)如果的半径为,,,求的长.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】
13.【答案】
14.【答案】5
15.【答案】10
16.【答案】
17.【答案】
18.【答案】
19.【答案】3或1
20.【答案】(1)
(2)解:设主桥拱半径为,
∵,,,
∴,,
在中,由勾股定理,得,
即,
解得,
因此,这座石拱桥主桥拱半径约为.
21.【答案】(1)解:,.答案不唯一.
(2)解:∵,∴.
设的半径为r,则.
在Rt△OEB中,
由勾股定理,得,
即,解得,
∴的半径为5.
22.【答案】(1)2
(2)
23.【答案】(1)
(2)
24.【答案】(1)证明:∵,
,
在与中,,
≌,
;
(2)解:过作与,于,连接,,
根据垂径定理得:,,
,
,
在与中,
,
≌,
,
,
四边形是正方形,
,
设,
则,
,
即:,
解得:,舍去,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
