浙教版初三数学3.4圆心角专题练习
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版初三数学3.4圆心角专题练习
一、选择题
1.图中是圆心角的是( )
A. B.
C. D.
2.如图中,,以C为圆心,为半径的圆交于点D,则的度数为( )
A. B. C. D.
3.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( )
A. B. C. D.
4.下列说法中,正确的是( )
A.同心圆的周长相等 B.面积相等的圆是等圆
C.相等的圆心角所对的弧相等 D.平分弧的弦一定经过圆心
5.如图所示,是的直径,,,则的度数为( )
A. B. C. D.
6.下列语句,错误的是( )
A.直径是弦
B.过圆心的弦是直径
C.平分弧的直径垂直于弧所对的弦
D.相等的圆心角所对的弧相等
7.下列说法中,正确的个数是( )
①三点确定一个圆;
②长度相等的两条弧一定是等弧;
③半径相等的两个圆是等圆;
④相等的圆心角所对的弦相等;
⑤长度相等的弦所对的优弧一定是等弧;
⑥四边形都有一个外接圆;
⑦平分弦的直径垂直于这条弦.
A.1个 B.2个 C.3个 D.4个
8.下列命题中不正确的是( )
A.在同圆或等圆中,相等的弦所对的弦心距相等
B.在同圆或等圆中,相等的圆心角所对的弧相等
C.在同圆或等圆中,相等的弧所对的弦相等
D.在同圆或等圆中,相等的弦所对的弧相等
9.如图,等边三角形ABC内接于⊙O,连结OA,OB,OC,延长AO,与BC交于点P,与⊙O交于点D,连结BD,CD.有以下结论:①四边形BDCO是菱形.②若⊙O的半径为r,则三角形ABC的边长为.③三角形ODC是等边三角形.④的度数为60°.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD= ,BC=1,则⊙O的半径为( )
A. B. C. D.
二、填空题
11.已知的直径为10,AB是的弦,,那么在中弦AB所对的圆心角度数为 .
12.如图,在⊙O中, ,则线段AB 2AC(填“>”“<”或“=”).
13.如图,是直径,点C是上一点,且,点D是的中点,点P是直径上一动点,则的最小值为 .
14.如图,已知、是的直径,,,则
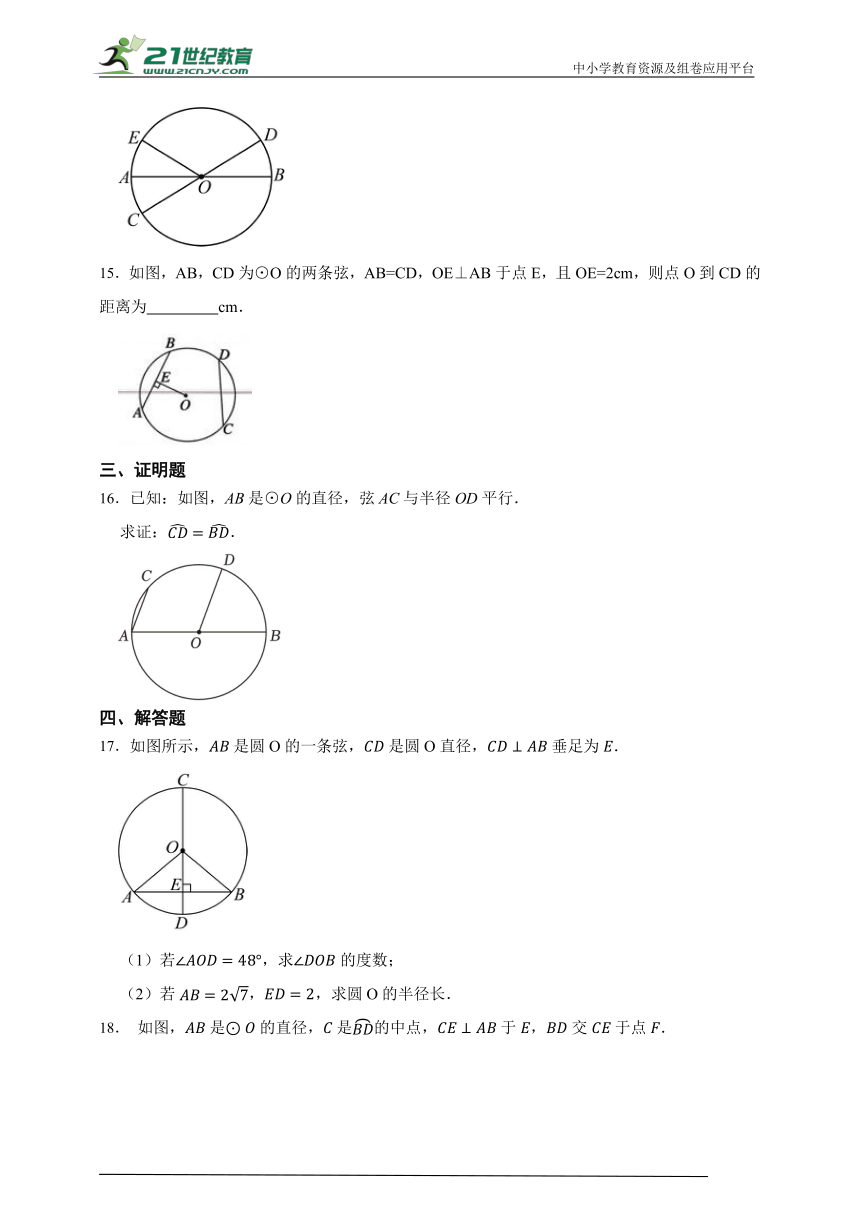
15.如图,AB,CD为⊙O的两条弦,AB=CD,OE⊥AB于点E,且OE=2cm,则点O到CD的距离为 cm.
三、证明题
16.已知:如图,AB是⊙O的直径,弦AC与半径OD平行.
求证:.
四、解答题
17.如图所示,是圆O的一条弦,是圆O直径,垂足为.
(1)若,求的度数;
(2)若,,求圆O的半径长.
18. 如图,是的直径,是的中点,于,交于点.
(1)求证:;
(2)若,,求的半径.
19.如图,在中,,以点O为圆心,为半径的圆交于点C,交于点D.
(1)若,则弧的度数为______.
(2)若,,求的长.
20.如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.
(1)求⊙O的半径;
(2)若∠EAB=∠EBA,求证:BF=2AH.
21.如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.
(1)当BC=6时,求线段OD的长.
(2)求DE的长.
(3)在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.
22.如图,A 是⊙O上的一个六等分点,B是的中点,P是直径MN上的一个动点,⊙O的半径为1.
(1) 找出当AP+BP取最小值时,点P的位置.
(2)求AP+BP的最小值.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】A
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】
12.【答案】<
13.【答案】
14.【答案】
15.【答案】2
16.【答案】证明:连接OC,
∵OC=OA,
∴∠A=∠C,
∵AC∥OD,
∴∠COD=∠C,∠BOD=∠A,
∴∠COD=∠BOD,
∴.
17.【答案】(1)的度数是;
(2)圆的半径长为.
18.【答案】(1)证明:延长交于点,
,
,
,
是的中点,
,
,
,
;
(2)解:是的直径,
,
,,
,
在中,,
的半径为.
19.【答案】(1)
(2)
20.【答案】(1)解:解:连接OA交BF于G,如图,⊙O的半径为r,
∵AD⊥OB,
∴AH=DH=4,
在Rt△OHA中,OH=r﹣2,OA=r,
∴r2=42+(r﹣2)2
,解得r=5,
即⊙O的半径为5;
(2)证明:连接CF,如图,
∵AD⊥OB,
∴弧AB=弧DB,
∵∠EAB=∠EBA,
∴弧BD=弧AF,
∴弧AB=弧AF,
∴OA⊥BG,
∴BG=FG,
∴∠OAH=∠OBG,
在△OAH和△OBG中,
,
∴△OAH≌△OBG(AAS),
∴AH=BG,
∴BF=2AH.
21.【答案】(1)解:∵OD⊥BC,
∴BD=BC= ×6=3,
∵∠BDO= 90°,OB=5,BD=3,
OD= =4,
即线段OD的长为4;
(2)解:如图,连结AB,DE,
∵∠AOB=90° ,OA=OB=5,
∴AB= .
∵OD⊥BC,OE⊥AC,
∴D,E分别是线段BC,AC的中点,
∴DE是△ABC的中位线,
∴DE=AB= ;
(3)解:∠DOE的度数不变,为45°,理由如下:
设OD交弧BC于点M,OE交弧AC于点N,
∵
∴
∴
∵
∴
即
22.【答案】(1)解:如图,过点A作弦AA'⊥MN于点E,连结BA',交MN于点P.
根据圆的轴对称性,AP= PA',∴AP+BP=PA'+BP.
根据两点之间线段最短,当A',P,B三点共线时,PA'+BP取得最小值BA',
即AP+BP=BA',∴点P位于A'B与MN的交点处.
(2)解:由题意,得∠AON=∠A'ON=60°,∠BON=30°,∴∠BOA'=90°.
又∵OB=OA'=1,∴BA'= ,即AP+BP的最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
浙教版初三数学3.4圆心角专题练习
一、选择题
1.图中是圆心角的是( )
A. B.
C. D.
2.如图中,,以C为圆心,为半径的圆交于点D,则的度数为( )
A. B. C. D.
3.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( )
A. B. C. D.
4.下列说法中,正确的是( )
A.同心圆的周长相等 B.面积相等的圆是等圆
C.相等的圆心角所对的弧相等 D.平分弧的弦一定经过圆心
5.如图所示,是的直径,,,则的度数为( )
A. B. C. D.
6.下列语句,错误的是( )
A.直径是弦
B.过圆心的弦是直径
C.平分弧的直径垂直于弧所对的弦
D.相等的圆心角所对的弧相等
7.下列说法中,正确的个数是( )
①三点确定一个圆;
②长度相等的两条弧一定是等弧;
③半径相等的两个圆是等圆;
④相等的圆心角所对的弦相等;
⑤长度相等的弦所对的优弧一定是等弧;
⑥四边形都有一个外接圆;
⑦平分弦的直径垂直于这条弦.
A.1个 B.2个 C.3个 D.4个
8.下列命题中不正确的是( )
A.在同圆或等圆中,相等的弦所对的弦心距相等
B.在同圆或等圆中,相等的圆心角所对的弧相等
C.在同圆或等圆中,相等的弧所对的弦相等
D.在同圆或等圆中,相等的弦所对的弧相等
9.如图,等边三角形ABC内接于⊙O,连结OA,OB,OC,延长AO,与BC交于点P,与⊙O交于点D,连结BD,CD.有以下结论:①四边形BDCO是菱形.②若⊙O的半径为r,则三角形ABC的边长为.③三角形ODC是等边三角形.④的度数为60°.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD= ,BC=1,则⊙O的半径为( )
A. B. C. D.
二、填空题
11.已知的直径为10,AB是的弦,,那么在中弦AB所对的圆心角度数为 .
12.如图,在⊙O中, ,则线段AB 2AC(填“>”“<”或“=”).
13.如图,是直径,点C是上一点,且,点D是的中点,点P是直径上一动点,则的最小值为 .
14.如图,已知、是的直径,,,则
15.如图,AB,CD为⊙O的两条弦,AB=CD,OE⊥AB于点E,且OE=2cm,则点O到CD的距离为 cm.
三、证明题
16.已知:如图,AB是⊙O的直径,弦AC与半径OD平行.
求证:.
四、解答题
17.如图所示,是圆O的一条弦,是圆O直径,垂足为.
(1)若,求的度数;
(2)若,,求圆O的半径长.
18. 如图,是的直径,是的中点,于,交于点.
(1)求证:;
(2)若,,求的半径.
19.如图,在中,,以点O为圆心,为半径的圆交于点C,交于点D.
(1)若,则弧的度数为______.
(2)若,,求的长.
20.如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.
(1)求⊙O的半径;
(2)若∠EAB=∠EBA,求证:BF=2AH.
21.如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.
(1)当BC=6时,求线段OD的长.
(2)求DE的长.
(3)在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.
22.如图,A 是⊙O上的一个六等分点,B是的中点,P是直径MN上的一个动点,⊙O的半径为1.
(1) 找出当AP+BP取最小值时,点P的位置.
(2)求AP+BP的最小值.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】A
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】
12.【答案】<
13.【答案】
14.【答案】
15.【答案】2
16.【答案】证明:连接OC,
∵OC=OA,
∴∠A=∠C,
∵AC∥OD,
∴∠COD=∠C,∠BOD=∠A,
∴∠COD=∠BOD,
∴.
17.【答案】(1)的度数是;
(2)圆的半径长为.
18.【答案】(1)证明:延长交于点,
,
,
,
是的中点,
,
,
,
;
(2)解:是的直径,
,
,,
,
在中,,
的半径为.
19.【答案】(1)
(2)
20.【答案】(1)解:解:连接OA交BF于G,如图,⊙O的半径为r,
∵AD⊥OB,
∴AH=DH=4,
在Rt△OHA中,OH=r﹣2,OA=r,
∴r2=42+(r﹣2)2
,解得r=5,
即⊙O的半径为5;
(2)证明:连接CF,如图,
∵AD⊥OB,
∴弧AB=弧DB,
∵∠EAB=∠EBA,
∴弧BD=弧AF,
∴弧AB=弧AF,
∴OA⊥BG,
∴BG=FG,
∴∠OAH=∠OBG,
在△OAH和△OBG中,
,
∴△OAH≌△OBG(AAS),
∴AH=BG,
∴BF=2AH.
21.【答案】(1)解:∵OD⊥BC,
∴BD=BC= ×6=3,
∵∠BDO= 90°,OB=5,BD=3,
OD= =4,
即线段OD的长为4;
(2)解:如图,连结AB,DE,
∵∠AOB=90° ,OA=OB=5,
∴AB= .
∵OD⊥BC,OE⊥AC,
∴D,E分别是线段BC,AC的中点,
∴DE是△ABC的中位线,
∴DE=AB= ;
(3)解:∠DOE的度数不变,为45°,理由如下:
设OD交弧BC于点M,OE交弧AC于点N,
∵
∴
∴
∵
∴
即
22.【答案】(1)解:如图,过点A作弦AA'⊥MN于点E,连结BA',交MN于点P.
根据圆的轴对称性,AP= PA',∴AP+BP=PA'+BP.
根据两点之间线段最短,当A',P,B三点共线时,PA'+BP取得最小值BA',
即AP+BP=BA',∴点P位于A'B与MN的交点处.
(2)解:由题意,得∠AON=∠A'ON=60°,∠BON=30°,∴∠BOA'=90°.
又∵OB=OA'=1,∴BA'= ,即AP+BP的最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
