3.2 从有理数到实数(教学课件)-七年级数学上册考试满分全攻略同步备课备考系列(浙教版2024)
文档属性
| 名称 | 3.2 从有理数到实数(教学课件)-七年级数学上册考试满分全攻略同步备课备考系列(浙教版2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-25 00:00:00 | ||
图片预览








文档简介
3.2 从有理数到实数
浙教版(2024) 七年级数学上册 第三章 实数
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解无理数的概念与分类,以及无理数与有理数的区别
2.会用逼近法判断无理数的范围
3.理解实数的概念与分类,以及实数与数轴的关系
情景导入
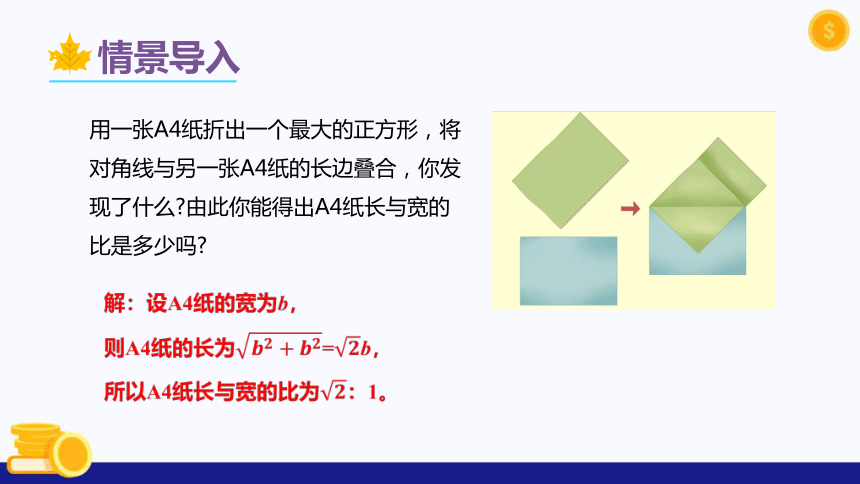
用一张A4纸折出一个最大的正方形,将对角线与另一张A4纸的长边叠合,你发现了什么?由此你能得出A4纸长与宽的比是多少吗?
解:设A4纸的宽为b,
则A4纸的长为????????+????????=????b,
所以A4纸长与宽的比为????:1。
?
新知探究
【合作学习】
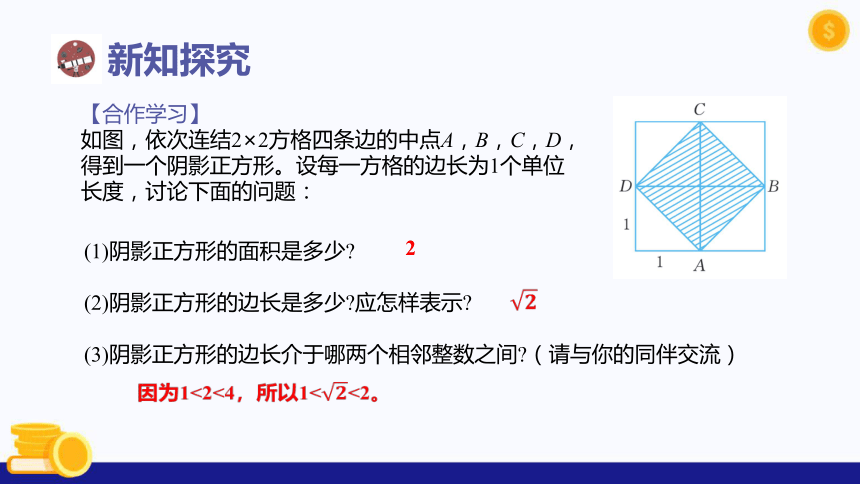
如图,依次连结2×2方格四条边的中点A,B,C,D,得到一个阴影正方形。设每一方格的边长为1个单位长度,讨论下面的问题:
(1)阴影正方形的面积是多少?
(2)阴影正方形的边长是多少?应怎样表示?
(3)阴影正方形的边长介于哪两个相邻整数之间?(请与你的同伴交流)
2
????
?
因为1<2<4,所以1?
我们可以通过计算,得到下表。
因为1<2<2,所以2不是整数。
下面让我们一起探究2的十分位、百分位、千分位等数位上的值。
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1.42<2<1.52
1.41.412<2<1.422
1.411.4142<2<1.4152
1.4141.41422<2<1.41432
1.41421.414212<2<1.414222
1.41421…
…
如此进行下去,可以得到一系列越来越接近2的近似值,
我们这种方法叫作逼近法。
?
事实上,2=1.414213562373095048801688724209698078569…,它既不是有限小数,也不是无限循环小数(不能化为分数)。
?
像2这种无限不循环小数叫作无理数。
?
无理数广泛存在着,例如:
π=3.1415926535897932384626433832795028841971693…;
????=1.7320508075688772935274463415058723669…;
?
任意写一个无限不循环小数,如1.010010001…(两个“1”之间依次多一个“0”),它也是无理数。
如果我们把整数看作小数部分为零的有限小数,那么有理数便是有限小数与无限循环小数的统称。
和有理数一样,无理数也可分为正无理数和负无理数。例如π,????,????,????都是正无理数, -π,-????,-????,-????都是负无理数。
?
有理数和无理数统称实数。
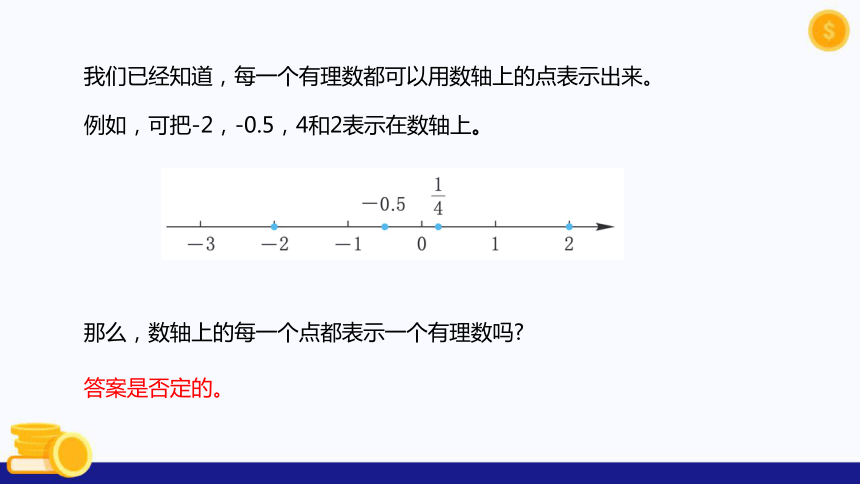
例如,可把-2,-0.5,4和2表示在数轴上。
我们已经知道,每一个有理数都可以用数轴上的点表示出来。
那么,数轴上的每一个点都表示一个有理数吗?
答案是否定的。
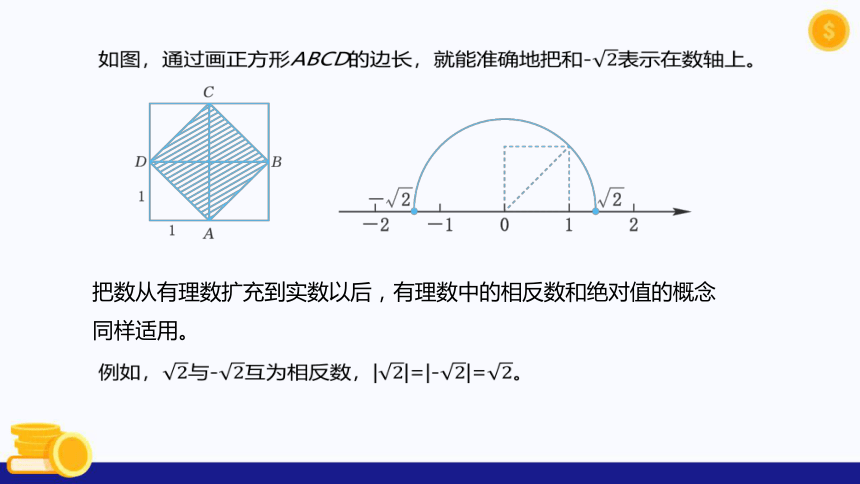
如图,通过画正方形ABCD的边长,就能准确地把和-2表示在数轴上。
?
例如,2与-2互为相反数,|2|=|-2|=2。
?
把数从有理数扩充到实数以后,有理数中的相反数和绝对值的概念同样适用。
在实数范围内,每一个实数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数。我们说实数和数轴上的点一一对应。
有理数的大小比较法则也适用于实数。
在数轴上表示的两个实数,右边的数总比左边的数大。
课本例题
83,?????,1.5,?3。
?
例 把下列实数表示在数轴上,并比较它们的大小(用“<”连接)。
分析:对于?????,?3等无理数,我们可以取其适当的近似值,
把它们近似地表示在数轴上,如取?????≈?3.1,?3≈?1.7。
?
解:把83,?????,1.5,?3表示在数轴上,如图。
?
所以??????
课本练习
1. 下列各数中,哪些是有理数?哪些是无理数?
1.7321,?18,0.36,?2,2????,0,?49。
?
有理数:1.7321,?18,0.36,0,?49;
?
无理数:?2,2????。
?
2.??填空:
1?3的相反数是??????????????????。
2?5=????????????????????。
???(3)一个数的绝对值是????2,这个数是(?????????????????????)。
?
3
?
5
?
????2 或 - ????2
?
3.用<>或数字填空:
1?因为1.732????????3????????1.742,
???????????????????所以1.73????????3????????1.74,
???????????????????所以3≈(??????????????)(精确到0.1)。
?
2?因为2.4492???????????6?????????2.4502,
???????所以2.449?????????6?????????2.450,
???????所以6≈(??????????????????)(精确到0.01)。
?
<
?
<
?
<
?
<
?
<
?
<
?
<
?
<
?
1.7
?
2.45
?
分层练习-基础
知识点1 实数的概念及分类
1. [2024·福建]下列实数中,无理数是( D )
A. -3
B. 0
C. ????????
D. ????
D
2. 下列说法中,正确的是( C )
A. 无理数包括正无理数、零和负无理数
B. 无限小数都是无理数
C. 正实数包括正有理数和正无理数
D. 实数可以分为正实数和负实数两类
C
3. [母题 教材P85作业题T1]把下列各数填在相应的横线上:
0,-???????????? ,-???? ,???????? ,-3.????????· ,+9,π,1.212 212
221…(相邻两个“1”之间依次多一个“2”).
(1)有理数: ?;
(2)无理数: ?
?.
?
0,-???????????? ,???????? ,-3.????????· ,+9
?
-???? ,π,1.212 212 221…(相邻两个“1”
?
之间依次多一个“2”)
知识点2 实数与数轴的对应关系
4. 如图,实数???? 在数轴上的对应点可能是点 ?.
?
5. 数轴上距离原点的距离为???????? 的点表示的数是 ?.
?
B
±????????
?
知识点3 实数的相反数与绝对值
6. [2024·宁波模拟]-5的绝对值是( D )
A. -????????
B. -????
C. ????
D. 5
7. 如果???? -1是a的相反数,则a的值是( B )
?
A. ???? -1
B. 1-????
C. ????
D. -????
D
B
知识点4 实数大小的比较
8. [2024·威海]下列各数中,最小的数是( A )
A. -2
B. -?????
C. -????????
D. -????
9. [母题 教材P85课内练习T3]估算???????? 的值在( C )
?
A. 1和2之间
B. 2和3之间
C. 3和4之间
D. 4和5之间
A
C
10. [2023·舟山]下面四个数中,比1小的正无理数是( A )
A. ????????
B. -??????
C. ????????
D. ????????
【点拨】
因为4<6<9,所以2<???? <3.
?
所以-???????? <???????? <???????? <1<???????? .
?
所以比1小的正无理数是???????? .
?
A
11. [2024·安徽]我国古代数学家张衡将圆周率取值为???????? ,祖冲之给出圆周率的一种分数形式的近似值为???????????? .比较大小:
???????? ?????????? (填“>”或“<”).
?
【点拨】
???????????????? =???????????????????? ,???????????? =10=???????????????????? ,
?
因为???????????????????? <???????????????????? ,所以???????????????? <???????????? .
?
所以???????? >???????????? .
?
>
12. [母题·教材P85作业题T4 2024·温州龙湾区期中]把|-4|,-3,-???????? ,???? 分别表示在数轴上,并比较它们的大小,用“<”连接.
?
【解】因为|-4|=4,???? ≈1.414,
?
所以将各数在数轴上表示出来,
如图:-3<-???????? <???? <|-4|.
?
[易错题]误认为带分数的数即为有理数
13. 下列说法正确的是( D )
A. ???????? 是有理数
B. ???????????? 是无理数
C. π-3.14是有理数
D. ???????????????? 是有理数
D
分层练习-巩固
14. 已知实数a=???? ,则下列关于a的说法正确的是( )
?
A. a是有理数
B. a不能表示在数轴上
C. 3<a<4
D. a的小数部分是???? -2
15. 若m,n是两个连续的整数,且m<???????? <n,则m+
n的相反数是 ?.
?
D
-7
16. 如图,面积为5的正方形ABCD的顶点A在数轴上,且点A表示的数为1.若点E也在数轴上(点E在点A的左侧),且AD=AE,则点E所表示的数为 ?.
1-????
?
17. [母题·教材P97目标与评定T4 2024·杭州萧山区期中]如图
①,4×4网格是由16个边长为1的小正方形组成的.
(1)图①中阴影正方形的顶点在网格的格点上,这个阴影
正方形的面积为 ,若这个阴影正方形的边长为
a,则a= ?;
10
????????
?
(2)估计阴影正方形的边长的值在相邻整数 和 ?之间;
3
4
(3)在图②的数轴上作出阴影正方形边长的值的对应点(要
求保留作图痕迹).
【解】如图②,点P表示的数是???????? .
?
分层练习-拓展
18. [2024·重庆巴南区期末]阅读下面文字,然后回答问题.给出定义:一个实数的整数部分是不大于这个数的最大整数,这个实数的小数部分为这个数与它的整数部分的差的绝对值.例如:2.4的整数部分为2,小数部分为2.4-2=0.4;???? 的整数部分为1,小数部分可用???? -1表示;-2.6的整数部分为-3,小数部分为|-2.6-(-3)|=0.4.
由此我们得到:如果???? =x+y,其中x是整数,且0<y<1,那么x=1,y=???? -1.
?
(1) 如果???? =a+b,其中a是整数,且0<b<1,
那么a= ,b= ?;
(2) 如果-???? =c+d,其中c是整数,且0<d<1,
那么c= ,d= ?;
?
2
???? -2
?
-3
3????
?
【解】因为m+???? =7+n,其中m是整数,且0<n<1,
所以易得m=5,n=???? -2.
所以|m-n|-(1-n)=|5-(????-2)|-?????(???????) =4,
所以|m-n|-(1-n)的平方根是±2.
?
(3)已知m+???? =7+n,其中m是整数,且0<n<1,求|m-n|-(1-n)的平方根.
?
课堂小结
无理数的概念:像2这种无限不循环小数叫作无理数。
无理数常见的三种类型:
1.含有π的绝大部分数,eg:2π,????2,π+1;
2.特定结构的无限不循环小数,eg:1.010010001…;
3.开不尽的方根,eg:2,3,5。
有理数与无理数的区别:
1.把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,无理数只能写成无限不循环小数;
2.有理数能够写成分数形式????????(m、n是整数,n≠0),而无理数不能。
无理数的分类:和有理数一样,无理数也可分为正无理数和负无理数。
?
课堂小结
实数的概念:有理数和无理数统称实数。
实数的分类:
实数与数轴:实数和数轴上的点一一对应。
实数比较大小:在数轴上表示的两个实数,右边的数总比左边的数大。
浙教版(2024) 七年级数学上册 第三章 实数
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解无理数的概念与分类,以及无理数与有理数的区别
2.会用逼近法判断无理数的范围
3.理解实数的概念与分类,以及实数与数轴的关系
情景导入
用一张A4纸折出一个最大的正方形,将对角线与另一张A4纸的长边叠合,你发现了什么?由此你能得出A4纸长与宽的比是多少吗?
解:设A4纸的宽为b,
则A4纸的长为????????+????????=????b,
所以A4纸长与宽的比为????:1。
?
新知探究
【合作学习】
如图,依次连结2×2方格四条边的中点A,B,C,D,得到一个阴影正方形。设每一方格的边长为1个单位长度,讨论下面的问题:
(1)阴影正方形的面积是多少?
(2)阴影正方形的边长是多少?应怎样表示?
(3)阴影正方形的边长介于哪两个相邻整数之间?(请与你的同伴交流)
2
????
?
因为1<2<4,所以1?
我们可以通过计算,得到下表。
因为1<2<2,所以2不是整数。
下面让我们一起探究2的十分位、百分位、千分位等数位上的值。
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1.42<2<1.52
1.41.412<2<1.422
1.411.4142<2<1.4152
1.4141.41422<2<1.41432
1.41421.414212<2<1.414222
1.41421…
…
如此进行下去,可以得到一系列越来越接近2的近似值,
我们这种方法叫作逼近法。
?
事实上,2=1.414213562373095048801688724209698078569…,它既不是有限小数,也不是无限循环小数(不能化为分数)。
?
像2这种无限不循环小数叫作无理数。
?
无理数广泛存在着,例如:
π=3.1415926535897932384626433832795028841971693…;
????=1.7320508075688772935274463415058723669…;
?
任意写一个无限不循环小数,如1.010010001…(两个“1”之间依次多一个“0”),它也是无理数。
如果我们把整数看作小数部分为零的有限小数,那么有理数便是有限小数与无限循环小数的统称。
和有理数一样,无理数也可分为正无理数和负无理数。例如π,????,????,????都是正无理数, -π,-????,-????,-????都是负无理数。
?
有理数和无理数统称实数。
例如,可把-2,-0.5,4和2表示在数轴上。
我们已经知道,每一个有理数都可以用数轴上的点表示出来。
那么,数轴上的每一个点都表示一个有理数吗?
答案是否定的。
如图,通过画正方形ABCD的边长,就能准确地把和-2表示在数轴上。
?
例如,2与-2互为相反数,|2|=|-2|=2。
?
把数从有理数扩充到实数以后,有理数中的相反数和绝对值的概念同样适用。
在实数范围内,每一个实数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数。我们说实数和数轴上的点一一对应。
有理数的大小比较法则也适用于实数。
在数轴上表示的两个实数,右边的数总比左边的数大。
课本例题
83,?????,1.5,?3。
?
例 把下列实数表示在数轴上,并比较它们的大小(用“<”连接)。
分析:对于?????,?3等无理数,我们可以取其适当的近似值,
把它们近似地表示在数轴上,如取?????≈?3.1,?3≈?1.7。
?
解:把83,?????,1.5,?3表示在数轴上,如图。
?
所以??????
课本练习
1. 下列各数中,哪些是有理数?哪些是无理数?
1.7321,?18,0.36,?2,2????,0,?49。
?
有理数:1.7321,?18,0.36,0,?49;
?
无理数:?2,2????。
?
2.??填空:
1?3的相反数是??????????????????。
2?5=????????????????????。
???(3)一个数的绝对值是????2,这个数是(?????????????????????)。
?
3
?
5
?
????2 或 - ????2
?
3.用<>或数字填空:
1?因为1.732????????3????????1.742,
???????????????????所以1.73????????3????????1.74,
???????????????????所以3≈(??????????????)(精确到0.1)。
?
2?因为2.4492???????????6?????????2.4502,
???????所以2.449?????????6?????????2.450,
???????所以6≈(??????????????????)(精确到0.01)。
?
<
?
<
?
<
?
<
?
<
?
<
?
<
?
<
?
1.7
?
2.45
?
分层练习-基础
知识点1 实数的概念及分类
1. [2024·福建]下列实数中,无理数是( D )
A. -3
B. 0
C. ????????
D. ????
D
2. 下列说法中,正确的是( C )
A. 无理数包括正无理数、零和负无理数
B. 无限小数都是无理数
C. 正实数包括正有理数和正无理数
D. 实数可以分为正实数和负实数两类
C
3. [母题 教材P85作业题T1]把下列各数填在相应的横线上:
0,-???????????? ,-???? ,???????? ,-3.????????· ,+9,π,1.212 212
221…(相邻两个“1”之间依次多一个“2”).
(1)有理数: ?;
(2)无理数: ?
?.
?
0,-???????????? ,???????? ,-3.????????· ,+9
?
-???? ,π,1.212 212 221…(相邻两个“1”
?
之间依次多一个“2”)
知识点2 实数与数轴的对应关系
4. 如图,实数???? 在数轴上的对应点可能是点 ?.
?
5. 数轴上距离原点的距离为???????? 的点表示的数是 ?.
?
B
±????????
?
知识点3 实数的相反数与绝对值
6. [2024·宁波模拟]-5的绝对值是( D )
A. -????????
B. -????
C. ????
D. 5
7. 如果???? -1是a的相反数,则a的值是( B )
?
A. ???? -1
B. 1-????
C. ????
D. -????
D
B
知识点4 实数大小的比较
8. [2024·威海]下列各数中,最小的数是( A )
A. -2
B. -?????
C. -????????
D. -????
9. [母题 教材P85课内练习T3]估算???????? 的值在( C )
?
A. 1和2之间
B. 2和3之间
C. 3和4之间
D. 4和5之间
A
C
10. [2023·舟山]下面四个数中,比1小的正无理数是( A )
A. ????????
B. -??????
C. ????????
D. ????????
【点拨】
因为4<6<9,所以2<???? <3.
?
所以-???????? <???????? <???????? <1<???????? .
?
所以比1小的正无理数是???????? .
?
A
11. [2024·安徽]我国古代数学家张衡将圆周率取值为???????? ,祖冲之给出圆周率的一种分数形式的近似值为???????????? .比较大小:
???????? ?????????? (填“>”或“<”).
?
【点拨】
???????????????? =???????????????????? ,???????????? =10=???????????????????? ,
?
因为???????????????????? <???????????????????? ,所以???????????????? <???????????? .
?
所以???????? >???????????? .
?
>
12. [母题·教材P85作业题T4 2024·温州龙湾区期中]把|-4|,-3,-???????? ,???? 分别表示在数轴上,并比较它们的大小,用“<”连接.
?
【解】因为|-4|=4,???? ≈1.414,
?
所以将各数在数轴上表示出来,
如图:-3<-???????? <???? <|-4|.
?
[易错题]误认为带分数的数即为有理数
13. 下列说法正确的是( D )
A. ???????? 是有理数
B. ???????????? 是无理数
C. π-3.14是有理数
D. ???????????????? 是有理数
D
分层练习-巩固
14. 已知实数a=???? ,则下列关于a的说法正确的是( )
?
A. a是有理数
B. a不能表示在数轴上
C. 3<a<4
D. a的小数部分是???? -2
15. 若m,n是两个连续的整数,且m<???????? <n,则m+
n的相反数是 ?.
?
D
-7
16. 如图,面积为5的正方形ABCD的顶点A在数轴上,且点A表示的数为1.若点E也在数轴上(点E在点A的左侧),且AD=AE,则点E所表示的数为 ?.
1-????
?
17. [母题·教材P97目标与评定T4 2024·杭州萧山区期中]如图
①,4×4网格是由16个边长为1的小正方形组成的.
(1)图①中阴影正方形的顶点在网格的格点上,这个阴影
正方形的面积为 ,若这个阴影正方形的边长为
a,则a= ?;
10
????????
?
(2)估计阴影正方形的边长的值在相邻整数 和 ?之间;
3
4
(3)在图②的数轴上作出阴影正方形边长的值的对应点(要
求保留作图痕迹).
【解】如图②,点P表示的数是???????? .
?
分层练习-拓展
18. [2024·重庆巴南区期末]阅读下面文字,然后回答问题.给出定义:一个实数的整数部分是不大于这个数的最大整数,这个实数的小数部分为这个数与它的整数部分的差的绝对值.例如:2.4的整数部分为2,小数部分为2.4-2=0.4;???? 的整数部分为1,小数部分可用???? -1表示;-2.6的整数部分为-3,小数部分为|-2.6-(-3)|=0.4.
由此我们得到:如果???? =x+y,其中x是整数,且0<y<1,那么x=1,y=???? -1.
?
(1) 如果???? =a+b,其中a是整数,且0<b<1,
那么a= ,b= ?;
(2) 如果-???? =c+d,其中c是整数,且0<d<1,
那么c= ,d= ?;
?
2
???? -2
?
-3
3????
?
【解】因为m+???? =7+n,其中m是整数,且0<n<1,
所以易得m=5,n=???? -2.
所以|m-n|-(1-n)=|5-(????-2)|-?????(???????) =4,
所以|m-n|-(1-n)的平方根是±2.
?
(3)已知m+???? =7+n,其中m是整数,且0<n<1,求|m-n|-(1-n)的平方根.
?
课堂小结
无理数的概念:像2这种无限不循环小数叫作无理数。
无理数常见的三种类型:
1.含有π的绝大部分数,eg:2π,????2,π+1;
2.特定结构的无限不循环小数,eg:1.010010001…;
3.开不尽的方根,eg:2,3,5。
有理数与无理数的区别:
1.把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,无理数只能写成无限不循环小数;
2.有理数能够写成分数形式????????(m、n是整数,n≠0),而无理数不能。
无理数的分类:和有理数一样,无理数也可分为正无理数和负无理数。
?
课堂小结
实数的概念:有理数和无理数统称实数。
实数的分类:
实数与数轴:实数和数轴上的点一一对应。
实数比较大小:在数轴上表示的两个实数,右边的数总比左边的数大。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
