浙教版八年级上册 第一章----二章特殊三角形测试卷(含答案)
文档属性
| 名称 | 浙教版八年级上册 第一章----二章特殊三角形测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 432.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-26 00:00:00 | ||
图片预览



文档简介
浙教版八上一-二章测试卷
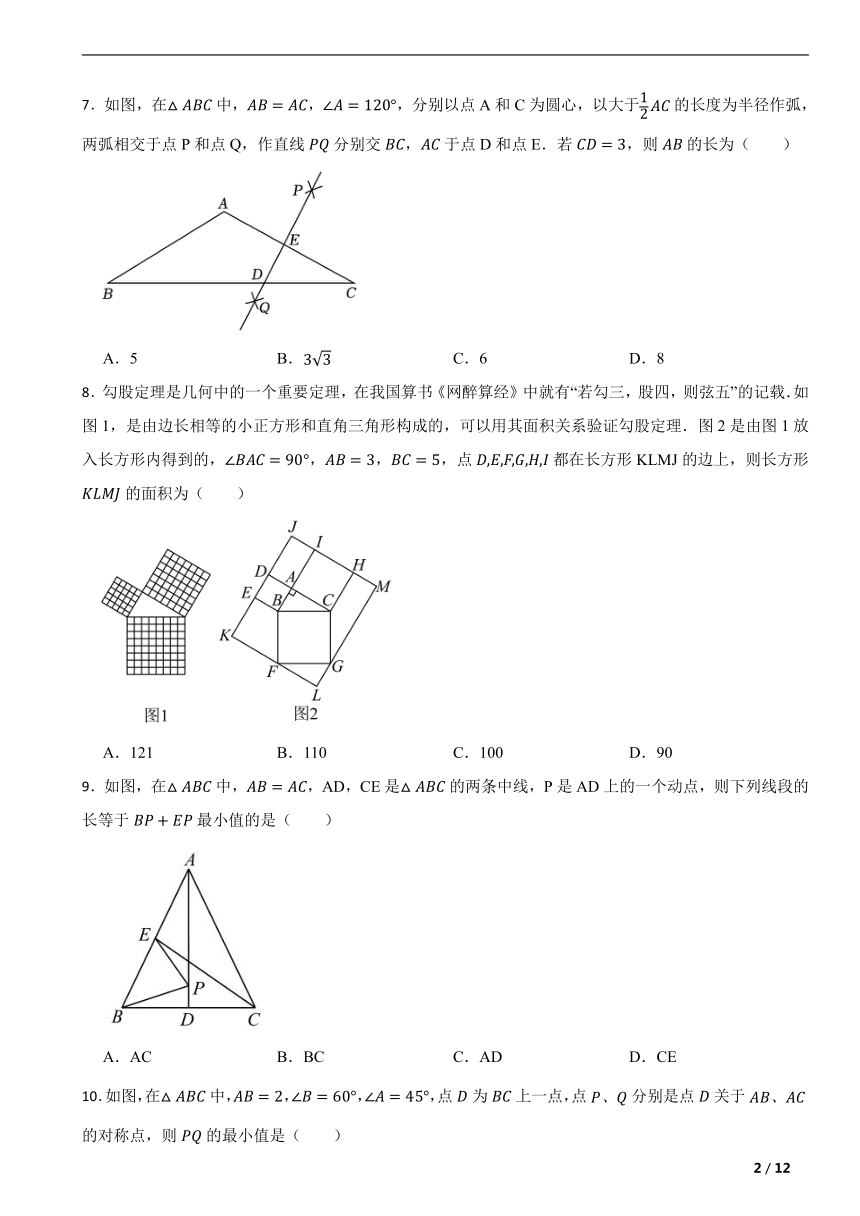
一、选择题(每小题3分,共30分)
1.某三角形的三边长分别为3,6,,则不可能是( )
A. B.6 C. D.
2.对于命题“如果∠1+∠2=180°,那么∠1≠∠2”,能说明它是假命题的反例是( )
A.∠1=150°,∠2=30° B.∠1=60°,∠2=60°
C.∠1=∠2=90° D.∠1=100°,∠2=40°
3.如图,某同学把一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带④去
4.等腰三角形的一个角为50°,则这个等腰三角形的底角为( )
A.65° B.65°或80° C.50°或65° D.40°
5.如图,小敏做了一个角平分仪,其中,,将仪器上的点A与的顶点R重合,调整和,使它们分别落在角的两边上,过点A、C画一条射线,就是的平分线.此角平分仪的画图原理是( )
A. B. C. D.
6.如图,在矩形中,,将矩形沿折叠,点A落在点E处,交于点F且,则的长为( )
A.2 B.2.5 C.3 D.4
7.如图,在中,,,分别以点A和C为圆心,以大于的长度为半径作弧,两弧相交于点P和点Q,作直线分别交,于点D和点E.若,则的长为( )
A.5 B. C.6 D.8
8.勾股定理是几何中的一个重要定理,在我国算书《网醉算经》中就有“若勾三,股四,则弦五”的记载.如图1,是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,,,,点都在长方形KLMJ的边上,则长方形的面积为( )
A.121 B.110 C.100 D.90
9.如图,在中,,AD,CE是的两条中线,P是AD上的一个动点,则下列线段的长等于最小值的是( )
A.AC B.BC C.AD D.CE
10.如图,在中,,,,点为上一点,点分别是点关于的对称点,则的最小值是( )
A. B. C.4 D.2
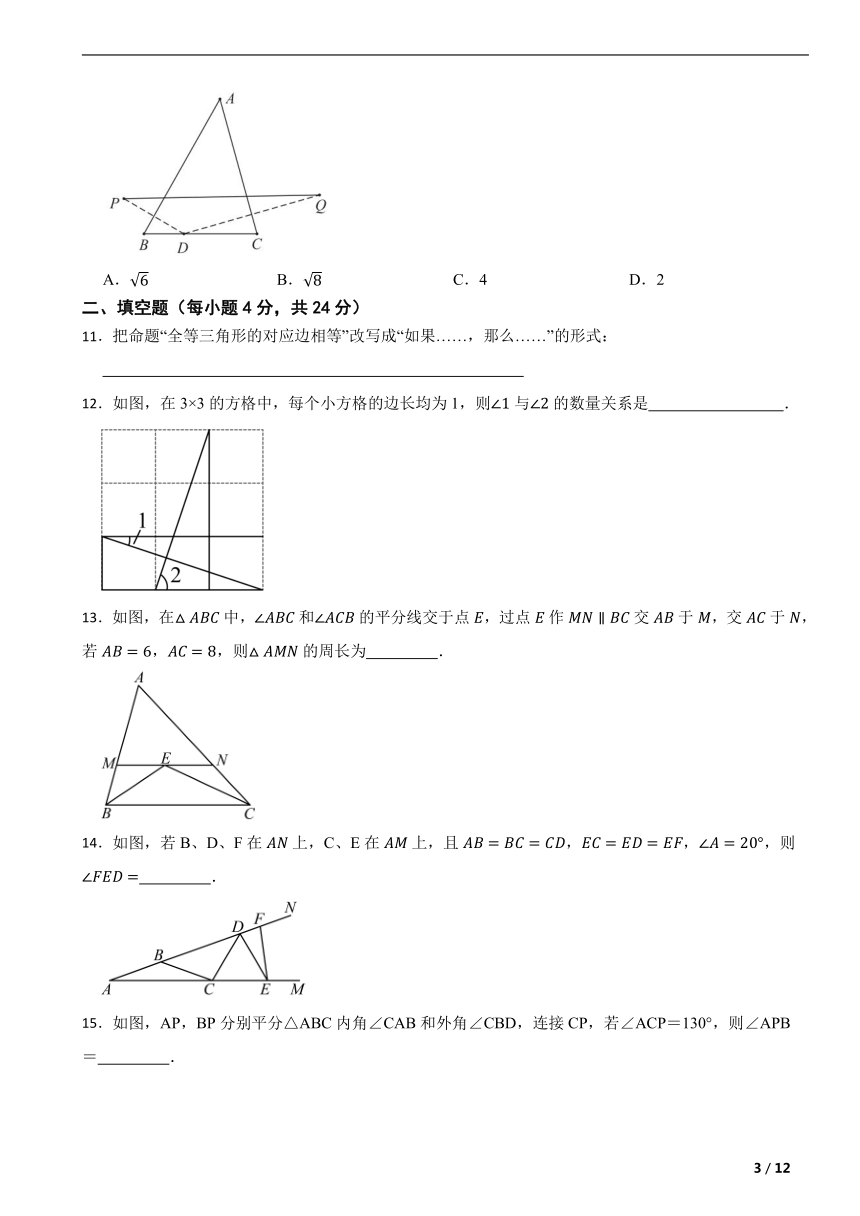
二、填空题(每小题4分,共24分)
11.把命题“全等三角形的对应边相等”改写成“如果……,那么……”的形式:
12.如图,在3×3的方格中,每个小方格的边长均为1,则与的数量关系是 .
13.如图,在中,和的平分线交于点,过点作交于,交于,若,,则的周长为 .
14.如图,若B、D、F在上,C、E在上,且,,,则 .
15.如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB= .
16.如图,,垂足为,,,射线,垂足为,动点从点出发以的速度沿射线运动,点为射线上一动点,满足,随着点运动而运动,当点运动 秒时,与点、、为顶点的三角形全等(时间不等于).
四、解答题(共46分)
(4分)17.推理填空:如图,已知,作的平分线,将直角尺如图摆放,使边与边重合,顶点落在边上,边与交于点,猜想是等腰三角形.
证明:平分(已知)
(①__________)
,
②__________(③__________)
④__________⑤__________(⑥__________)
(⑦__________)
是等腰三角形.
(5分)18.如图,在中,,,求和的度数.
(5分)19.如图,点D在△ABC中,∠BDC=90°,AB=6,AC=BD=4,CD=2.
(1)求BC的长;
(2)求图中阴影部分的面积.
(6分)20.已知:如图,在△ABC中,BF⊥AC于点F,CG⊥AB于点G,D是BC的中点,DE⊥FG于点E.求证:GE=EF.
(8分)21.如图1,居家网课学习时,小华先将笔记本电脑水平放置在桌子上,显示屏与底板所在水平线的夹角,侧面示意图如图2;如图3,使用时为了散热,他在底板下垫入散热架后,电脑转到位置,侧面示意图如图4.已知,于点,,.
(1)求的长;
(2)垫入散热架后,显示屏顶部比原来升高了多少cm?
(8分)22.(1)阅读理解
如图①,在中,若,,为边上的中线,则的取值范围是_______.
解决此问题可用如下方法:延长到K,使,再连接,这样就把、、转化到了中,利用三角形三边关系即可得出结论.
(2)实践探究
如图②在中,点D是边的中点,,交边于E,交边于F,连接,判断与的大小关系,并说明理由;
(3)拓展延伸
我们发现直角三角形三边之间存在一种关系,若直角三角形的两直角边分别为a、b,斜边为c,那么.等腰三角形顶角的平分线,底边上的高线和中线互相重合.如图③,在(2)的条件下,当,,的长度是关于x、y的方程组的两个根,求的面积.
(10分)23.如图1,等腰三角形中,是边上的中线,延长至点,使,连结.
(1)求证:是等腰直角三角形.
(2)如图2,过点作的垂线交于点,试判断的形状,并说明理由.
(3)如图3,在(2)的基础上,,连结,若是直角三角形,求的长.
答案解析部分
1.D
2.C
由∠1+∠2=180°可知∠1和∠2互补,当∠1=∠2=90°时,∠1+∠2=90°+90°=180°,故此命题为假命题.
3.B
4.C
当50°是等腰三角形的顶角时,则底角为(180°﹣50°)× =65°;
当50°是底角时也可以.
5.A
6.C
7.B
8.B
9.D
解:如图连接PC,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴PB=PC,
∴PB+PE=PC+PE,
∵PE+PC≥CE,
∴P、C、E共线时,PB+PE的值最小,最小值为CE的长度,
10.A
如图,连接AP,AD,AQ,过点A作AE⊥BC于点E
∵点分别是点关于的对称点
∴AB垂直平分PD,AC垂直平分QD
∴AP=AD=AQ
∴∠PAB=∠DAB,∠QAC=∠DAC
∵∠BAC=45°即∠DAB+∠DAC=45°
∴∠PAB+∠DAB+∠QA+∠DAC=45°×2=90°
∴∠PAQ=90°
∴
∴当AD最小时 ,PQ最小
AD最小为AE
∵∠B=60°,∠AEB=90°
∴∠BAE=30°
∴
∴
∴
11.如果两个三角形全等,那么这两个三角形的对应边相等
12.
13.14
14.
15.40°
解:∵平分,平分,
∴,,
又∵,,
∴
∴
∴
如图示,过P作于点,于点,延长线于点,
∵平分,平分,
∴,,
即
∴平分,
∴
又∵
∴
∴
∴
∴
16.或或
解:①当在线段上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
则,
∴,
即时间为秒,不合题意舍去;
②当在线段上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
∴,
∴点的运动时间为秒;
③当在射线上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
∴,
∴点的运动时间为秒;
④当在射线上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
则,
∴,
∴点的运动时间为秒;
综上,当点运动或或秒时,与点、、为顶点的三角形全等,
17.①角平分线的定义;②;③两直线平行,内错角相等;④;⑤;⑥等量代换;⑦等角对等边
18.;
19.(1)解:∵∠BDC=90°,BD=4,CD=2,∴BC==2.
(2)解:∵AB=6,AC=4,
∴AC2+BC2=42+(2)2=16+20=36=62=AB2,
∴△ACB是直角三角形,∠ACB=90°,
∴S阴影=S△ACB-S△BDC=×4×2-×4×2=4-4.
20.解:连结 DG,DF.
∵CG⊥AB,
∴∠CGB=90°,
∵D 是BC 的中点,
∴DG= BC.
同理得DF=BC.
∴ DG=DF,
∵DE⊥FG,
∴ GE=EF
21.(1)OA的长为20cm
(2)显示屏顶部比原来升高了
22.(1);(2);(3).
23.(1)证明:是边上的中线(证全等亦可)
又是等腰直角三角形
(2)解:是等腰三角形(同角的余角相等)
是边上的中线(等腰三角形三线合一)
是等腰直角三角形
,即
是等腰三角形
(3)解:①
(证亦可)
设,则
,解得,即
②
作,同理可证
设,则
,解得
1 / 1
一、选择题(每小题3分,共30分)
1.某三角形的三边长分别为3,6,,则不可能是( )
A. B.6 C. D.
2.对于命题“如果∠1+∠2=180°,那么∠1≠∠2”,能说明它是假命题的反例是( )
A.∠1=150°,∠2=30° B.∠1=60°,∠2=60°
C.∠1=∠2=90° D.∠1=100°,∠2=40°
3.如图,某同学把一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带④去
4.等腰三角形的一个角为50°,则这个等腰三角形的底角为( )
A.65° B.65°或80° C.50°或65° D.40°
5.如图,小敏做了一个角平分仪,其中,,将仪器上的点A与的顶点R重合,调整和,使它们分别落在角的两边上,过点A、C画一条射线,就是的平分线.此角平分仪的画图原理是( )
A. B. C. D.
6.如图,在矩形中,,将矩形沿折叠,点A落在点E处,交于点F且,则的长为( )
A.2 B.2.5 C.3 D.4
7.如图,在中,,,分别以点A和C为圆心,以大于的长度为半径作弧,两弧相交于点P和点Q,作直线分别交,于点D和点E.若,则的长为( )
A.5 B. C.6 D.8
8.勾股定理是几何中的一个重要定理,在我国算书《网醉算经》中就有“若勾三,股四,则弦五”的记载.如图1,是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,,,,点都在长方形KLMJ的边上,则长方形的面积为( )
A.121 B.110 C.100 D.90
9.如图,在中,,AD,CE是的两条中线,P是AD上的一个动点,则下列线段的长等于最小值的是( )
A.AC B.BC C.AD D.CE
10.如图,在中,,,,点为上一点,点分别是点关于的对称点,则的最小值是( )
A. B. C.4 D.2
二、填空题(每小题4分,共24分)
11.把命题“全等三角形的对应边相等”改写成“如果……,那么……”的形式:
12.如图,在3×3的方格中,每个小方格的边长均为1,则与的数量关系是 .
13.如图,在中,和的平分线交于点,过点作交于,交于,若,,则的周长为 .
14.如图,若B、D、F在上,C、E在上,且,,,则 .
15.如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB= .
16.如图,,垂足为,,,射线,垂足为,动点从点出发以的速度沿射线运动,点为射线上一动点,满足,随着点运动而运动,当点运动 秒时,与点、、为顶点的三角形全等(时间不等于).
四、解答题(共46分)
(4分)17.推理填空:如图,已知,作的平分线,将直角尺如图摆放,使边与边重合,顶点落在边上,边与交于点,猜想是等腰三角形.
证明:平分(已知)
(①__________)
,
②__________(③__________)
④__________⑤__________(⑥__________)
(⑦__________)
是等腰三角形.
(5分)18.如图,在中,,,求和的度数.
(5分)19.如图,点D在△ABC中,∠BDC=90°,AB=6,AC=BD=4,CD=2.
(1)求BC的长;
(2)求图中阴影部分的面积.
(6分)20.已知:如图,在△ABC中,BF⊥AC于点F,CG⊥AB于点G,D是BC的中点,DE⊥FG于点E.求证:GE=EF.
(8分)21.如图1,居家网课学习时,小华先将笔记本电脑水平放置在桌子上,显示屏与底板所在水平线的夹角,侧面示意图如图2;如图3,使用时为了散热,他在底板下垫入散热架后,电脑转到位置,侧面示意图如图4.已知,于点,,.
(1)求的长;
(2)垫入散热架后,显示屏顶部比原来升高了多少cm?
(8分)22.(1)阅读理解
如图①,在中,若,,为边上的中线,则的取值范围是_______.
解决此问题可用如下方法:延长到K,使,再连接,这样就把、、转化到了中,利用三角形三边关系即可得出结论.
(2)实践探究
如图②在中,点D是边的中点,,交边于E,交边于F,连接,判断与的大小关系,并说明理由;
(3)拓展延伸
我们发现直角三角形三边之间存在一种关系,若直角三角形的两直角边分别为a、b,斜边为c,那么.等腰三角形顶角的平分线,底边上的高线和中线互相重合.如图③,在(2)的条件下,当,,的长度是关于x、y的方程组的两个根,求的面积.
(10分)23.如图1,等腰三角形中,是边上的中线,延长至点,使,连结.
(1)求证:是等腰直角三角形.
(2)如图2,过点作的垂线交于点,试判断的形状,并说明理由.
(3)如图3,在(2)的基础上,,连结,若是直角三角形,求的长.
答案解析部分
1.D
2.C
由∠1+∠2=180°可知∠1和∠2互补,当∠1=∠2=90°时,∠1+∠2=90°+90°=180°,故此命题为假命题.
3.B
4.C
当50°是等腰三角形的顶角时,则底角为(180°﹣50°)× =65°;
当50°是底角时也可以.
5.A
6.C
7.B
8.B
9.D
解:如图连接PC,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴PB=PC,
∴PB+PE=PC+PE,
∵PE+PC≥CE,
∴P、C、E共线时,PB+PE的值最小,最小值为CE的长度,
10.A
如图,连接AP,AD,AQ,过点A作AE⊥BC于点E
∵点分别是点关于的对称点
∴AB垂直平分PD,AC垂直平分QD
∴AP=AD=AQ
∴∠PAB=∠DAB,∠QAC=∠DAC
∵∠BAC=45°即∠DAB+∠DAC=45°
∴∠PAB+∠DAB+∠QA+∠DAC=45°×2=90°
∴∠PAQ=90°
∴
∴当AD最小时 ,PQ最小
AD最小为AE
∵∠B=60°,∠AEB=90°
∴∠BAE=30°
∴
∴
∴
11.如果两个三角形全等,那么这两个三角形的对应边相等
12.
13.14
14.
15.40°
解:∵平分,平分,
∴,,
又∵,,
∴
∴
∴
如图示,过P作于点,于点,延长线于点,
∵平分,平分,
∴,,
即
∴平分,
∴
又∵
∴
∴
∴
∴
16.或或
解:①当在线段上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
则,
∴,
即时间为秒,不合题意舍去;
②当在线段上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
∴,
∴点的运动时间为秒;
③当在射线上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
∴,
∴点的运动时间为秒;
④当在射线上,时,∵AB=PN,∠ACB=∠PBN=90°,
∴,
则,
∴,
∴点的运动时间为秒;
综上,当点运动或或秒时,与点、、为顶点的三角形全等,
17.①角平分线的定义;②;③两直线平行,内错角相等;④;⑤;⑥等量代换;⑦等角对等边
18.;
19.(1)解:∵∠BDC=90°,BD=4,CD=2,∴BC==2.
(2)解:∵AB=6,AC=4,
∴AC2+BC2=42+(2)2=16+20=36=62=AB2,
∴△ACB是直角三角形,∠ACB=90°,
∴S阴影=S△ACB-S△BDC=×4×2-×4×2=4-4.
20.解:连结 DG,DF.
∵CG⊥AB,
∴∠CGB=90°,
∵D 是BC 的中点,
∴DG= BC.
同理得DF=BC.
∴ DG=DF,
∵DE⊥FG,
∴ GE=EF
21.(1)OA的长为20cm
(2)显示屏顶部比原来升高了
22.(1);(2);(3).
23.(1)证明:是边上的中线(证全等亦可)
又是等腰直角三角形
(2)解:是等腰三角形(同角的余角相等)
是边上的中线(等腰三角形三线合一)
是等腰直角三角形
,即
是等腰三角形
(3)解:①
(证亦可)
设,则
,解得,即
②
作,同理可证
设,则
,解得
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
