第一章----二章 有理数的运算 综合练习(含答案)2024--2025学年浙教版七年级数学上册
文档属性
| 名称 | 第一章----二章 有理数的运算 综合练习(含答案)2024--2025学年浙教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-26 17:16:47 | ||
图片预览



文档简介
第一-二章练习2024--2025学年浙教版七年级数学上册
一、选择题
1.中国是世界上最早使用正负数的国家,用正负数可以表示具有相反意义的量.如果盈余200元记作元,那么元表示的意义是( )
A.卖出50元 B.亏损50元 C.支出50元 D.遗失50元
2.“鸭嘴兽”被认为是世界上最奇怪的哺乳动物,因为它身上有许多怪异的特征:嘴里没有牙齿;汗液像牛奶;后脚有毒刺等,且最古老的鸭嘴兽于南美洲的6100万年前的地层被发现.将“6100万”用科学记数法表示为,其中n为( )
A.7 B.8 C.9 D.10
3.已知a,b在数轴上的位置如图所示,则下列结论错误的有( )
A. B. C. D.
4.已知,,且,则的值等于( )
A.7和 B.7
C. D.以上答案都不对
5.一滴墨水洒在数轴上,根据图中标出的数值判断墨迹盖住的整数个数是( )
A.4 B.3 C.2 D.1
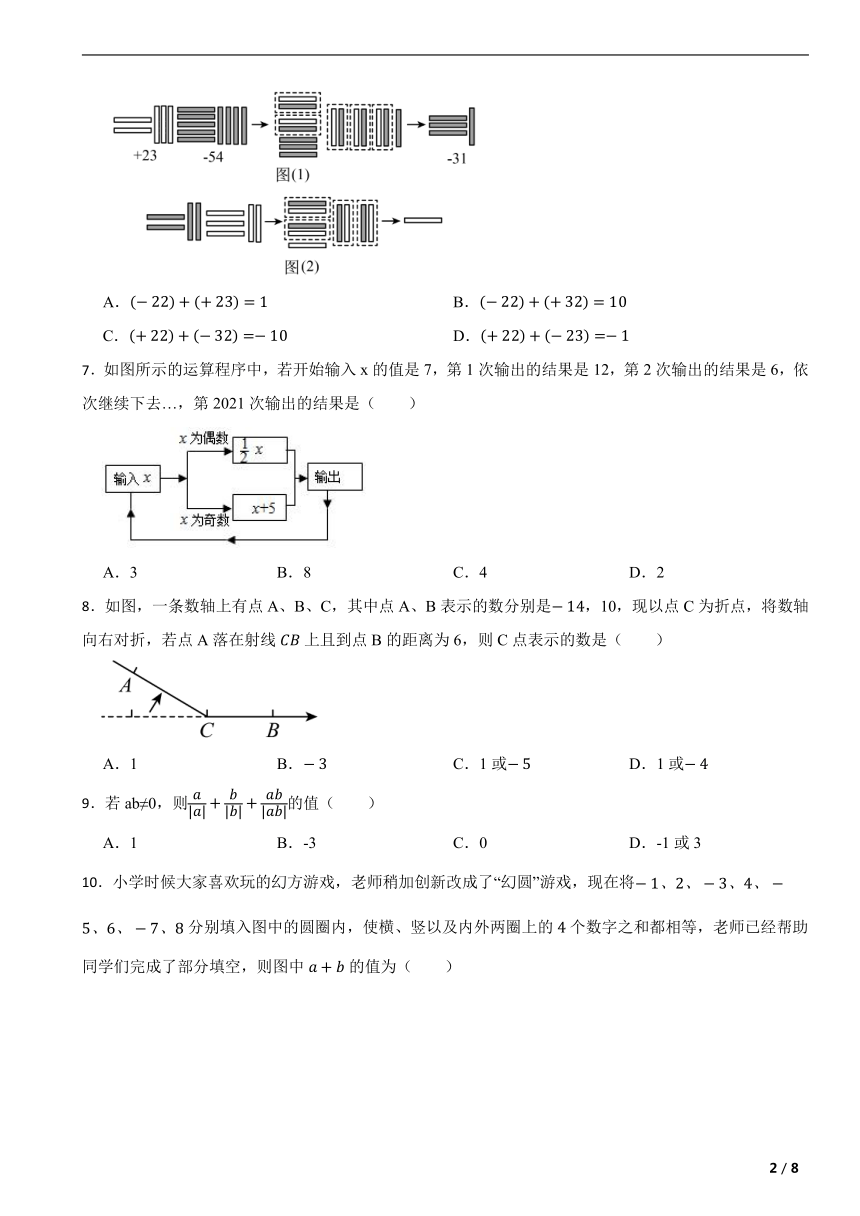
6.魏晋时期数学家刘徽在《九章算术注》中用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(白色为正,黑色为负),图(1)表示的是的计算过程,则图(2)表示的计算过程是( )
A. B.
C. D.
7.如图所示的运算程序中,若开始输入x的值是7,第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2021次输出的结果是( )
A.3 B.8 C.4 D.2
8.如图,一条数轴上有点A、B、C,其中点A、B表示的数分别是,10,现以点C为折点,将数轴向右对折,若点A落在射线上且到点B的距离为6,则C点表示的数是( )
A.1 B. C.1或 D.1或
9.若ab≠0,则的值( )
A.1 B.-3 C.0 D.-1或3
10.小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将分别填入图中的圆圈内,使横、竖以及内外两圈上的个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中的值为( )
A.或 B.或 C.或 D.或
二、填空题
11.一次数学测试,以80分为基准,90分记作+10分,那么70分应记作 .
12.一个加数是,和是,则另一个加数是 .
13.的相反数的绝对值是 .
14.如图,将一刻度尺放在数轴上(数轴的单位长度是),刻度尺上“”和“”分别对应数轴上的和,那么刻度尺上“”对应数轴上的数为 .
15.按一定规律排列的一列数依次为:,……按此规律排列下去,第7个数是 .
16.同学们都知道: 表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,同理, 可以表示数轴上有理数 所对应的点到-2和-3所对应的点的距离之和,则 的最小值为 .
三、解答题
17.把下列各数相应的序号填入相应的横线内:
①;②3;③;④;⑤;⑥15;⑦0;⑧.
(1)分数:______;
(2)正有理数:______;
(3)有理数:______.
18.如图的数轴上,每小格的宽度相等.
(1)填空:数轴上点表示的数是 ,点表示的数是 .
(2)点表示的数是,点表示的数是,请在数轴上分别画出点和点的位置.
(3)将四个点所表示的数按从大到小的顺序排列,用“>”连接.
19.已知,b的相反数是2,c是最大的负整数,d+3没有倒数.
(1)若,求的值;
(2)若,求的值.
20.“滴滴”司机沈师傅从上午在东西方向的绿谷大道上营运,共连续运载十批乘客.若规定向东为正,向西为负,沈师傅营运十批乘客里程如下:(单位:千米),,,,,,,,,.
(1)将最后一批乘客送到目的地时,沈师傅距离第一批乘客出发地的东面还是西面?距离多少千米?
(2)上午沈师傅开车的平均速度是多少?
(3)若“滴滴”的收费标准为:起步价8元(不超过3千米),超过3千米,超过部分每千米2元.则沈师傅在上午一共收入多少元?
21.有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13(J,Q,K分别代表11,12,13;A表示1)之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4可作运算:(1+2+3)×4=24.(注意上述运算与4×(1+2+3)应视为相同的运算)
(1)小明抽到了3,4,5,2;小聪抽到了J,2,10,5。这两组牌都能算出“24”点吗?为什么?
(2)如果算式中允许包含乘方运算,两组牌中你能列出含乘方运算的算式吗?
22.如图在数轴上点表示数a,B点表示数b,a、b满足;
(1)点表示的数为 ;点表示的数为; ;
(2)若在原点处放一挡板,一小球甲从点处以1个单位/秒的速度向左运动;同时另一小球乙从点处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为(秒),
①当时,甲小球到原点的距离= ,乙小球到原点的距离= ;
当时,甲小球到原点的距离= ;乙小球到原点的距离= ;
②试探究:甲,乙两小球到原点的距离可能相等吗 若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
答案解析部分
1.B
2.A
3.D
4.D
5.B
6.B
7.C
解:根据题意可知:
开始输入x的值是7,第1次输出的结果是12,
第2次输出的结果是6,
第3次输出的结果是3,
第4次输出的结果是8,
第5次输出的结果是4,
第6次输出的结果是2,
第7次输出的结果是1,
第8次输出的结果是6,
依次继续下去,
…,
发现规律:从第2次开始,6,3,8,4,2,1,每次6个数循环,
因为(2021﹣1)÷6=336…4,
所以第2021次输出的结果与第5次输出的结果一样是4.
8.C
9.D
解:分两种情况:(1)当ab>0时,a,b同正或同负.
当a,b同正时,= 1+1+1=3.
当a,b同负时,= -1-1+1=-1.
当ab<0时,a,b一正一负.
当a正b负时,= 1-1-1=-1.
当a负b正时,= -1+1-1=-1.
综上所述,的值为-1或3 .
10.A
11.-10
12.
13.
解:的相反数为,的绝对值为.
14.
15.
解:观察可知:数列中所有数的分母为连续奇数,
∴第7个数的分母为13,
∵3=2+1,5=22+1,9=23+1,17=24+1,33=25+1,65=26+1,…,
∴第7个数的分子为27+1=129,
又∵数列中奇为正,偶为负,
∴第7个数是.
16.1
解:当 时, ,
∴
当 时, , ,
当 时, , ,
∴ 的最小值为:1
17.(1)③④;
(2)②③⑥;
(3)①②③④⑥⑤⑦
18.(1);
(2)解:如图.
(3)解:由数轴可知,
19.(1)解:a=-5,b=-2,a+b=-7
(2)解:a=5,b=-2,c=-1,d=-3,a-3b-2c+d=5-3×(-2)-2×(-1)+(-3)=10
20.(1)在距离第一批乘客出发地的东面,距离是3千米
(2)44千米小时
(3)130元
21.(1)解:这两组牌都能算出“24”点.
理由如下: 小明 :(3+4+5)×2.
小聪 :11×2+10÷5.
(2)解:能. 算式如下:
52-4+3;52-11+10.
22.(1)-2;4
(2)3;2;5;2
解:(1)∵ a、b满足,
∴a+2=0且b-4=0,
解之:a=-2,b=4;
∵在数轴上点表示数a,B点表示数b,
∴点A表示的数为-2,点B表示的数为4.
故答案为:-2,4.
(2)①∵ 一小球甲从点处以1个单位/秒的速度向左运动,点A表示的数为-2
当t=1时,甲小球到原点的距离为|-2-1×1|=3;乙小球到原点的距离为|4-2×1|=2;
当t=3时,甲小球到原点的距离为|-2-1×3|=5;乙小球到原点的距离为|4-2×3|=2;
故答案为:3;2;5;2.
②甲,乙两小球到原点的距离可能相等
当0<t≤2时,t+2=4-2t,
解之:;
当t>2时,
t+2=2t-4
解之:t=6;
甲,乙两小球到原点的距离相等时经历的时间为6秒或秒.(3)分情况讨论:当0<t≤2时,利用甲,乙两小球到原点的距离相等,可得到关于t的方程,解方程求出t的值;当t>2时,利用甲,乙两小球到原点的距离相等,可得到关于t的方程,解方程求出t的值;综上所述可得到符合题意的t的值.
1 / 1
一、选择题
1.中国是世界上最早使用正负数的国家,用正负数可以表示具有相反意义的量.如果盈余200元记作元,那么元表示的意义是( )
A.卖出50元 B.亏损50元 C.支出50元 D.遗失50元
2.“鸭嘴兽”被认为是世界上最奇怪的哺乳动物,因为它身上有许多怪异的特征:嘴里没有牙齿;汗液像牛奶;后脚有毒刺等,且最古老的鸭嘴兽于南美洲的6100万年前的地层被发现.将“6100万”用科学记数法表示为,其中n为( )
A.7 B.8 C.9 D.10
3.已知a,b在数轴上的位置如图所示,则下列结论错误的有( )
A. B. C. D.
4.已知,,且,则的值等于( )
A.7和 B.7
C. D.以上答案都不对
5.一滴墨水洒在数轴上,根据图中标出的数值判断墨迹盖住的整数个数是( )
A.4 B.3 C.2 D.1
6.魏晋时期数学家刘徽在《九章算术注》中用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(白色为正,黑色为负),图(1)表示的是的计算过程,则图(2)表示的计算过程是( )
A. B.
C. D.
7.如图所示的运算程序中,若开始输入x的值是7,第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2021次输出的结果是( )
A.3 B.8 C.4 D.2
8.如图,一条数轴上有点A、B、C,其中点A、B表示的数分别是,10,现以点C为折点,将数轴向右对折,若点A落在射线上且到点B的距离为6,则C点表示的数是( )
A.1 B. C.1或 D.1或
9.若ab≠0,则的值( )
A.1 B.-3 C.0 D.-1或3
10.小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将分别填入图中的圆圈内,使横、竖以及内外两圈上的个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中的值为( )
A.或 B.或 C.或 D.或
二、填空题
11.一次数学测试,以80分为基准,90分记作+10分,那么70分应记作 .
12.一个加数是,和是,则另一个加数是 .
13.的相反数的绝对值是 .
14.如图,将一刻度尺放在数轴上(数轴的单位长度是),刻度尺上“”和“”分别对应数轴上的和,那么刻度尺上“”对应数轴上的数为 .
15.按一定规律排列的一列数依次为:,……按此规律排列下去,第7个数是 .
16.同学们都知道: 表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,同理, 可以表示数轴上有理数 所对应的点到-2和-3所对应的点的距离之和,则 的最小值为 .
三、解答题
17.把下列各数相应的序号填入相应的横线内:
①;②3;③;④;⑤;⑥15;⑦0;⑧.
(1)分数:______;
(2)正有理数:______;
(3)有理数:______.
18.如图的数轴上,每小格的宽度相等.
(1)填空:数轴上点表示的数是 ,点表示的数是 .
(2)点表示的数是,点表示的数是,请在数轴上分别画出点和点的位置.
(3)将四个点所表示的数按从大到小的顺序排列,用“>”连接.
19.已知,b的相反数是2,c是最大的负整数,d+3没有倒数.
(1)若,求的值;
(2)若,求的值.
20.“滴滴”司机沈师傅从上午在东西方向的绿谷大道上营运,共连续运载十批乘客.若规定向东为正,向西为负,沈师傅营运十批乘客里程如下:(单位:千米),,,,,,,,,.
(1)将最后一批乘客送到目的地时,沈师傅距离第一批乘客出发地的东面还是西面?距离多少千米?
(2)上午沈师傅开车的平均速度是多少?
(3)若“滴滴”的收费标准为:起步价8元(不超过3千米),超过3千米,超过部分每千米2元.则沈师傅在上午一共收入多少元?
21.有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13(J,Q,K分别代表11,12,13;A表示1)之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4可作运算:(1+2+3)×4=24.(注意上述运算与4×(1+2+3)应视为相同的运算)
(1)小明抽到了3,4,5,2;小聪抽到了J,2,10,5。这两组牌都能算出“24”点吗?为什么?
(2)如果算式中允许包含乘方运算,两组牌中你能列出含乘方运算的算式吗?
22.如图在数轴上点表示数a,B点表示数b,a、b满足;
(1)点表示的数为 ;点表示的数为; ;
(2)若在原点处放一挡板,一小球甲从点处以1个单位/秒的速度向左运动;同时另一小球乙从点处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为(秒),
①当时,甲小球到原点的距离= ,乙小球到原点的距离= ;
当时,甲小球到原点的距离= ;乙小球到原点的距离= ;
②试探究:甲,乙两小球到原点的距离可能相等吗 若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
答案解析部分
1.B
2.A
3.D
4.D
5.B
6.B
7.C
解:根据题意可知:
开始输入x的值是7,第1次输出的结果是12,
第2次输出的结果是6,
第3次输出的结果是3,
第4次输出的结果是8,
第5次输出的结果是4,
第6次输出的结果是2,
第7次输出的结果是1,
第8次输出的结果是6,
依次继续下去,
…,
发现规律:从第2次开始,6,3,8,4,2,1,每次6个数循环,
因为(2021﹣1)÷6=336…4,
所以第2021次输出的结果与第5次输出的结果一样是4.
8.C
9.D
解:分两种情况:(1)当ab>0时,a,b同正或同负.
当a,b同正时,= 1+1+1=3.
当a,b同负时,= -1-1+1=-1.
当ab<0时,a,b一正一负.
当a正b负时,= 1-1-1=-1.
当a负b正时,= -1+1-1=-1.
综上所述,的值为-1或3 .
10.A
11.-10
12.
13.
解:的相反数为,的绝对值为.
14.
15.
解:观察可知:数列中所有数的分母为连续奇数,
∴第7个数的分母为13,
∵3=2+1,5=22+1,9=23+1,17=24+1,33=25+1,65=26+1,…,
∴第7个数的分子为27+1=129,
又∵数列中奇为正,偶为负,
∴第7个数是.
16.1
解:当 时, ,
∴
当 时, , ,
当 时, , ,
∴ 的最小值为:1
17.(1)③④;
(2)②③⑥;
(3)①②③④⑥⑤⑦
18.(1);
(2)解:如图.
(3)解:由数轴可知,
19.(1)解:a=-5,b=-2,a+b=-7
(2)解:a=5,b=-2,c=-1,d=-3,a-3b-2c+d=5-3×(-2)-2×(-1)+(-3)=10
20.(1)在距离第一批乘客出发地的东面,距离是3千米
(2)44千米小时
(3)130元
21.(1)解:这两组牌都能算出“24”点.
理由如下: 小明 :(3+4+5)×2.
小聪 :11×2+10÷5.
(2)解:能. 算式如下:
52-4+3;52-11+10.
22.(1)-2;4
(2)3;2;5;2
解:(1)∵ a、b满足,
∴a+2=0且b-4=0,
解之:a=-2,b=4;
∵在数轴上点表示数a,B点表示数b,
∴点A表示的数为-2,点B表示的数为4.
故答案为:-2,4.
(2)①∵ 一小球甲从点处以1个单位/秒的速度向左运动,点A表示的数为-2
当t=1时,甲小球到原点的距离为|-2-1×1|=3;乙小球到原点的距离为|4-2×1|=2;
当t=3时,甲小球到原点的距离为|-2-1×3|=5;乙小球到原点的距离为|4-2×3|=2;
故答案为:3;2;5;2.
②甲,乙两小球到原点的距离可能相等
当0<t≤2时,t+2=4-2t,
解之:;
当t>2时,
t+2=2t-4
解之:t=6;
甲,乙两小球到原点的距离相等时经历的时间为6秒或秒.(3)分情况讨论:当0<t≤2时,利用甲,乙两小球到原点的距离相等,可得到关于t的方程,解方程求出t的值;当t>2时,利用甲,乙两小球到原点的距离相等,可得到关于t的方程,解方程求出t的值;综上所述可得到符合题意的t的值.
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
