5.6三角形的中位线

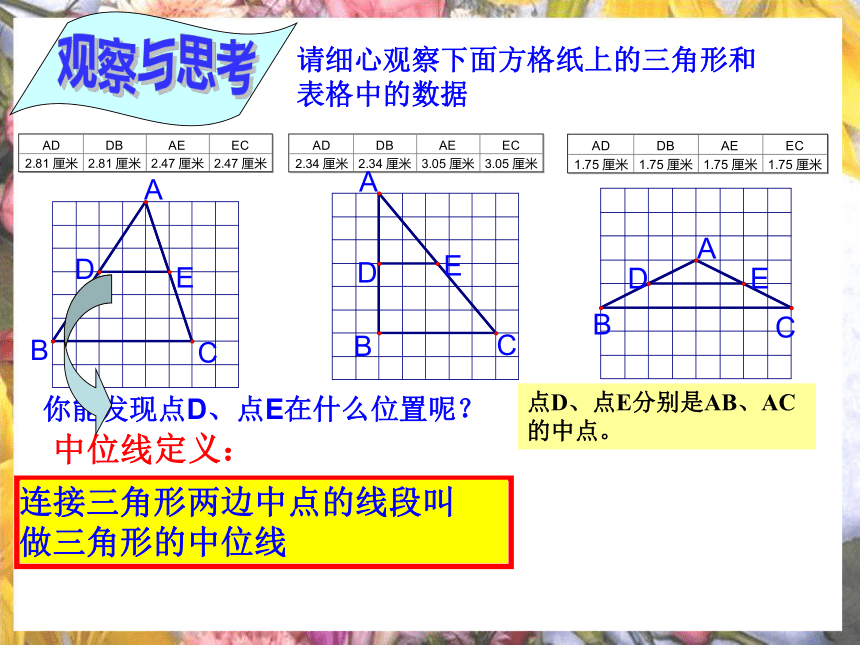
课件17张PPT。请细心观察下面方格纸上的三角形和
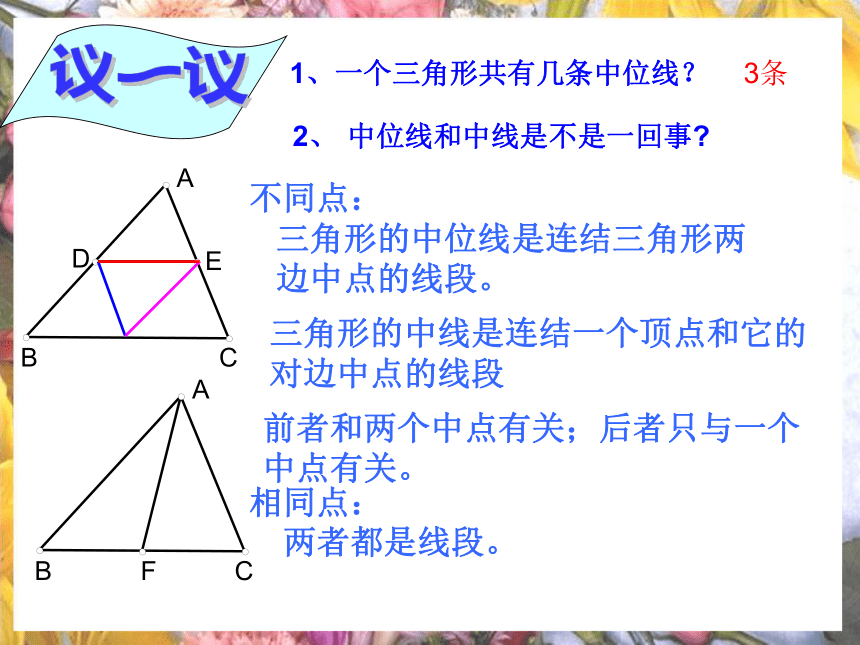
表格中的数据 你能发现点D、点E在什么位置呢？观察与思考点D、点E分别是AB、AC的中点。定义：5.6 三角形的中位线霞关中学 李甫状 2、 中位线和中线是不是一回事?不同点： 三角形的中位线是连结三角形两边中点的线段。两者都是线段。三角形的中线是连结一个顶点和它的
对边中点的线段相同点：前者和两个中点有关；后者只与一个
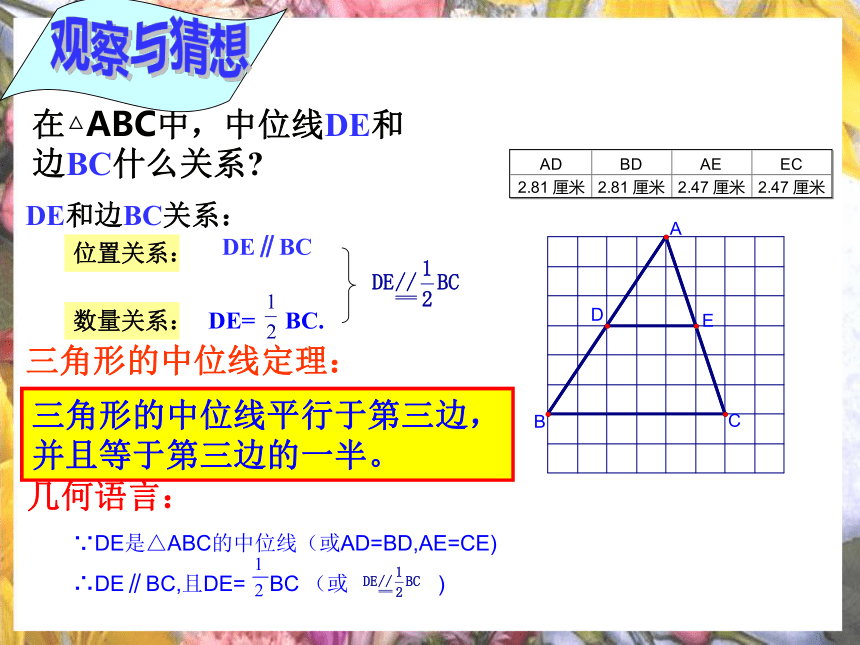
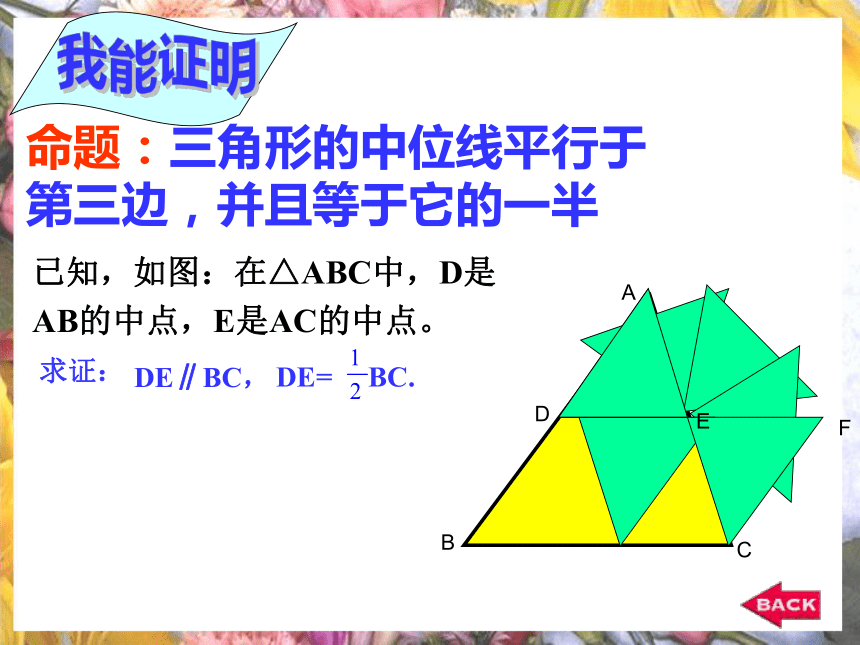
中点有关。议一议1、一个三角形共有几条中位线？3条三角形的中位线定理：几何语言：DE和边BC关系：数量关系：位置关系：DE∥BC在△ABC中，中位线DE和边BC什么关系?观察与猜想∵DE是△ABC的中位线（或AD=BD,AE=CE)我能证明命题：三角形的中位线平行于
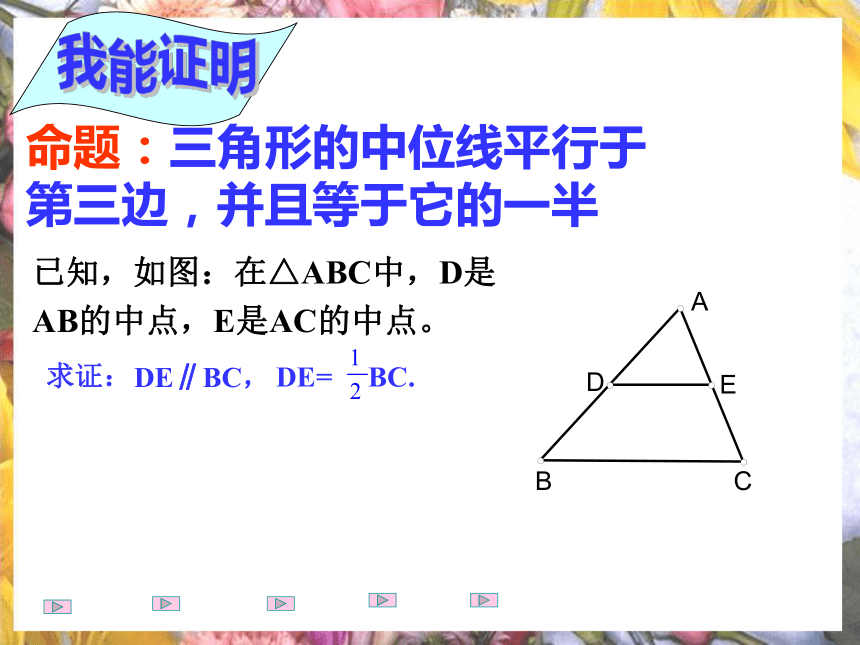
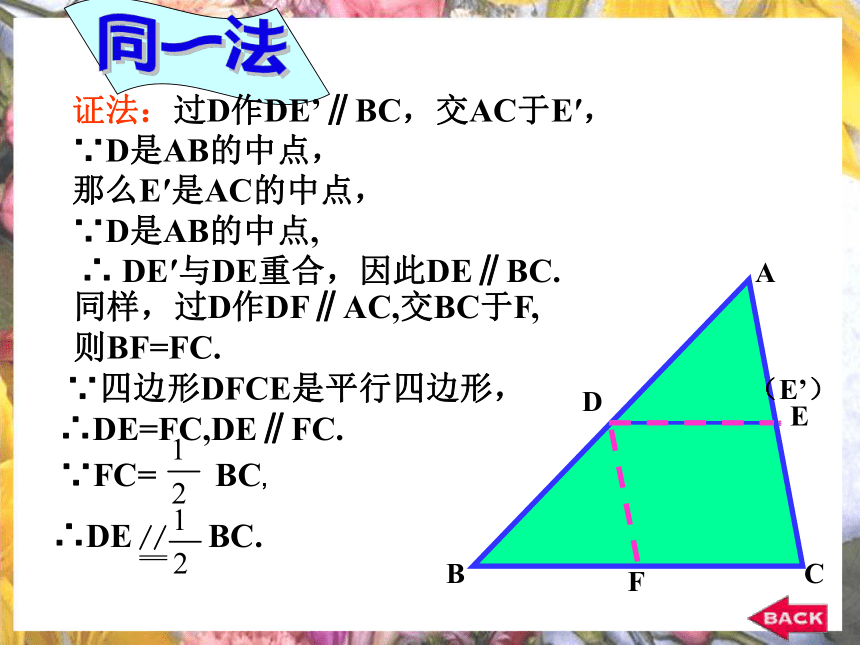
第三边，并且等于它的一半已知，如图：在△ABC中，D是
AB的中点，E是AC的中点。我能证明命题：三角形的中位线平行于
第三边，并且等于它的一半已知，如图：在△ABC中，D是
AB的中点，E是AC的中点。ABCDEF证明：如图，过E作AB的平行线交BC于F，自A作BC的平行线交FE于G
（4）若M、N分别是BD、BF的中点
∴MN∥_____， MN=1/2_____（5）三角形ABC的周长为18，则三角形
DEF的周长是_____
已知如图，D、E、F分别是△ABC
三边的中点，求下列各小题。（1）若AB=6cm 则 EF=_____cm（2）若DF=5cm 则 AC=_____cm（3）∵D、F是AB、BC的中点
∴DF∥_____310ACDFDF9已知：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。证明：连结AC∴四边形EFGH是平行四边形∴例题解析有中点连线而无三角形,要作辅助
线产生三角形。求证：四边形EFGH是平行四边形。∵ 点E、点F是AB、BC的中点∴EF是△ABC的中位线变式练习 （1）?顺次连结平行四边形各边中点所得的四边形是_________？平行四边形（2）顺次连结梯形各边中点所得的四边形是______________？平行四边形顺次连结四边形四条边的中点，
所得的四边形是平行四边形。ABCDE 为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB，AC的中点D、E，若测出DE的长，就能求出池塘BC的长，你知道为什么吗？想一想： 3.已知: 如图,DE,EF是⊿ABC的两条中位线.求证:四边形BFED是平行四边形. 4.如图,DE是⊿ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.课内练习3、已知：如图，△ABC是锐角三角形。分别以AB，AC为边向外侧作等边三角形ABM和等边三角形CAN，D，E，F分别是MB，BC，CN的中点，连结DE，FE，求证：DE=FE挑战自我连接三角形两边中点的线段叫做三角形的中位线。中位线的概念：小结中位线和中线的
变换的区别和联系：前者和两个中点有关；后者只与一个
中点有关。顺次连结四边形四条边的中点， 所得的四边形是平行四边形.顺次连结平行四边形各边中点所得的四边形是平行四边形。顺次连结梯形各边中点所得的四边形是平行四边形。顺次连结正方形各边中点所得的四边形是平行四边形。再见