4.5整式的加减 课件(共37张PPT)-七年级数学上册精品课堂(浙教版2024)
文档属性
| 名称 | 4.5整式的加减 课件(共37张PPT)-七年级数学上册精品课堂(浙教版2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 15:58:21 | ||
图片预览











文档简介
(共37张PPT)
4.5 整式的加减
第4章代数式
教学目标
01
理解去括号法则,并熟练运用去括号法则进行运算
02
理解添括号法则,并熟练运用添括号法则进行运算
03
能利用合并同类项和去括号法则进行整式的加减运算
04
掌握整式的加减——化简求值的一般步骤
去括号
从大拇指开始,按食指、中指、无名指、小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5,…。当第四次数到中指时,这个数是几 当第n次数到中指时,这个数是多少 当第200次数到中指时,这个数是多少
01
课堂引入
第一次数到中指时,这个数是3,
第二次数到中指时,这个数是3+5=8,
第三次数到中指时,这个数是3+5×2=13,
01
课堂引入
第四次数到中指时,这个数是3+5×3=18,
…,以此类推,
第n次数到中指时,这个数是3+5×n=5n+3,
第200次数到中指时,这个数是3+5×200=1003。
01
课堂引入
如图,要计算这个图形的面积,
你有几种不同的方法 请计算结果。
法一:将这个图形看作一个大长方形,
则面积为:3(x+3)。
法二:将这个图形看作一个小长方形和一个正方形拼接而成,
则面积为:3x+9。
01
课堂引入
小贴士:代数式中的字母表示的是数,
因此数的运算律也适用于代数式。
用不同方法得到的结果相等,由此你发现了什么
3(x+3)=3x+9
乘法分配律
根据分配律,有:
+(a-b+c)
=1×(a-b+c)
=a-b+c;
02
知识精讲
-a+b-c
=(-1)×(a-b+c)
=-(a-b+c)。
02
知识精讲
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
去括号
eg:+(a-3)=a-3;-(a-3)=-a+3。
一般地,我们有代数式运算的去括号法则:
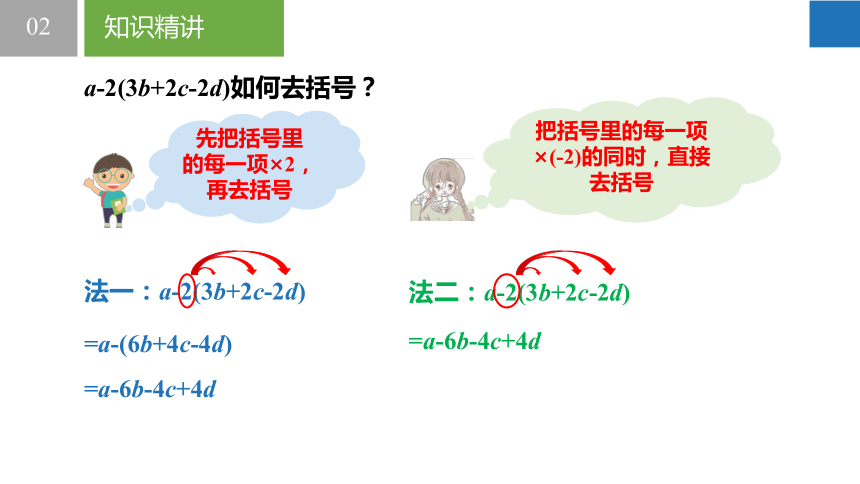
a-2(3b+2c-2d)如何去括号?
先把括号里的每一项×2,再去括号
把括号里的每一项×(-2)的同时,直接去括号
02
知识精讲
法一:a-2(3b+2c-2d)
=a-(6b+4c-4d)
=a-6b-4c+4d
法二:a-2(3b+2c-2d)
=a-6b-4c+4d
例1-1、去括号:
(1)a+(b+c-d)=________;
(2)a-(b+c)=________;
(3)a-(b-c+d)=________;
(4)a-b-(c-d)=________;
(5)a+b-(-c-d)=________。
a+b+c-d
a-b-c
a-b+c-d
a-b-c+d
a-b+c+d
03
典例精析
例1-2、代数式-[x-(y-z)]去括号后应得( )
A.-x+y-z B.-x-y+z C.-x-y-z D.-x+y+z
【分析】原式=-(x-y+z)=-x+y-z
A
【其他小妙招】x前面1个“-”,即-x;
y前面2个“-”,即y;
z前面3个“-”,即-z。
03
典例精析
例2-1、去括号:
(1)a-2(b+5c)=________________________;
(2)a-3(-3b+2c-d)=________________________。
a-(2b+10c)=a-2b-10c
a-(-9b+6c-3d)=a+9b-6c+3d
先用方法一巩固基础
03
典例精析
例2-2、下列各项去括号正确的是( )
A. -3(m+n)-mn=-3m+3n-mn
B. x2-2(2x-y+2)=x2-4x-2y+4
C. ab-5(-a+3)=ab+5a-3
D. -(5x-3y)+4(2xy-y2)=-5x+3y+8xy-4y2
D
-3m-3n-mn
x2-4x+2y-4
ab+5a-15
总结——常见两类错误:
①符号要变,但没变;
②括号前的系数该乘,但漏乘。
再用方法二提速
03
典例精析
例3、化简:
(1)(x-2y+1)-(2x-y-1); (2)2(2x-3y)-3(x+3y);
解:原式
=x-2y+1-2x+y+1
=(x-2x)+(-2y+y)+(1+1)
=-x-y+2
解:原式
=4x-6y-3x-9y
=(4x-3x)+(-6y-9y)
=x-15y
03
典例精析
(3)-3(a-2b-3)-5(a+b-1); (4)6a2-2[5a-(2a2-a)+a2]。
解:原式
=-3a+6b+9-5a-5b+5
03
典例精析
=(-3a-5a)+(6b-5b)+(9+5)
=-8a+b+14
解:原式
=6a2-2(5a-2a2+a+a2)
=6a2-2(6a-a2)
=6a2-12a+2a2
=(6a2+2a2)-12a
=8a2-12a
例4、化简:3(a+b)-7(a+b)-5(x+y)+9(x+y)。
先将(a+b)、(x+y)看作整体,合并同类项,再去括号
解:原式
=-4(a+b)+4(x+y)
=-4a-4b+4x+4y
03
典例精析
例5、求(3x2+xy+2y)-2(5xy-4x2+y)的值,其中x=-1,y=-。
解:(3x2+xy+2y)-2(5xy-4x2+y)
=3x2+xy+2y-10xy+8x2-2y
=(3x2+8x2)+(xy-10xy)+(2y-2y)
=11x2-9xy,
03
典例精析
先化简
后求值
当x=-1,y=-时,原式=11×(-1)2-9×(-1)×(-)=11-3=8。
添括号
已知+(a-b+c)=a-b+c,-(a-b+c)=-a+b-c,这两个等式从左到右看是去括号,原理是乘法分配律,那么从右往左看呢?
从右往左看是添括号,原理是乘法分配律的逆用。
01
课堂引入
将两个式子左右颠倒:
a-b+c=+(a-b+c);-a+b-c=-(a-b+c)。
02
知识精讲
添括号法则:
添加括号和“+”号,括号里各项都不变号;
添加括号和“-”号,括号里各项都改变符号。
添括号
eg:a-3=+(a-3);-a+3=-(a-3)。
别忘了再从右往左看,检验结果的正确性哦!
例1、填空:
(1)x+y-z=x+( );
(2)x-y-z=x-( );
(3)3a-2b+7c=3a-( );
(4)-2x2+y-z-5=-(2x2+5)-( )。
y-z
y+z
2b-7c
-y+z
03
典例精析
例2、下列添括号正确的是( )
A. -b-c=-(b-c)
B. -2x+6y=-2(x-6y)
C. a-b=+(a-b)
D. x-y-1=x-(y-1)
C
-(b+c)
-2(x-3y)
x-y+1
03
典例精析
例3、填空:
不改变多项式3b3-2ab2+4a2b-6a3的值,把后三项放在前面是“-”号的括号中,则3b3-2ab2+4a2b-6a3=3b3-2( )。
ab2-2a2b+3a3
03
典例精析
整式的加减
如图,甲、乙两个零件截面的面积哪一个较大 大多少 把结果填在下面的横线上。
截面甲的面积是________________,
截面乙的面积是________________,
甲、乙两个截面面积的差是
(________)-(________)。
01
课堂引入
πr2-2ab
πr2-1.5ab
πr2-2ab
πr2-1.5ab
(πr2-2ab)-(πr2-1.5ab)
=πr2-2ab-πr2+1.5ab
=-0.5ab
去括号
合并同类项
02
知识精讲
整式的加减可以归结为去括号与合并同类项。
整式的加减
在解决实际问题时,经常需要把若干个整式相加减。
【尝试】求5a2-7a+2与-3a2+2a-1的差。
02
知识精讲
解:5a2-7a+2-(-3a2+2a-1)
=5a2-7a+2+3a2-2a+1
=8a2-9a+3。
例1、已知A-2B=8a2-7ab,B=-4a2+6ab+7,求多项式A。
解:∵A-2B=8a2-7ab,B=-4a2+6ab+7,
∴A=2B+8a2-7ab
=2(-4a2+6ab+7)+8a2-7ab
=-8a2+12ab+14+8a2-7ab
=5ab+14。
03
典例精析
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
解:法一:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
=-2x2+x-1-2x2+4x-5
=-4x2+5x-6,
03
典例精析
A-(2x2-4x+5)
=-4x2+5x-6-(2x2-4x+5)
=-4x2+5x-6-2x2+4x-5
=-6x2+9x-11。
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
法二:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
∴A-(2x2-4x+5)
=-2x2+x-1-2(2x2-4x+5)
=-2x2+x-1-4x2+8x-10
=-6x2+9x-11。
03
典例精析
整式的化简求值
例1、已知M=3a2+4ab-1,N=a2-2ab-1,
(1)用含a、b的代数式表示M-3N;
(2)若a、b满足(a-1)2+|b-2|=0,求M-3N的值。
03
典例精析
解:(1)M-3N
=3a2+4ab-1-3(a2-2ab-1)
=3a2+4ab-1-3a2+6ab+3
=10ab+2;
(2)∵(a-1)2+|b-2|=0,
∴a=1,b=2,
∴M-3N=10ab+2=10×1×2+2=22。
03
典例精析
【题型】整式的加减——化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将字母表示的数代入化简后的式子计算。
例2、先化简,再求值:已知8x2ay与-3x4y2+b是同类项,且A=a2+ab-2b2,B=3a2-ab-6b2,求2B-3(B-A)的值。
∵8x2ay与-3x4y2+b是同类项,
∴2a=4,1=2+b,
∴a=2,b=-1,
∴2B-3(B-A)=4ab=4×2×(-1)=-8。
解:2B-3(B-A)
=2B-3B+3A
=3A-B
=3(a2+ab-2b2)-(3a2-ab-6b2)
=3a2+3ab-6b2-3a2+ab+6b2
=4ab;
03
典例精析
课后总结
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
符号语言:+(a-b+c)=a-b+c;-(a-b+c)=-a+b-c。
添括号法则:
添加括号和“+”号,括号里各项都不变号;
添加括号和“-”号,括号里各项都改变符号。
符号语言:a-b+c=+(a-b+c);-a+b-c=-(a-b+c)。
课后总结
整式的加减可以归结为去括号与合并同类项。
【题型】整式的加减——化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将字母表示的数代入化简后的式子计算。
4.5 整式的加减
第4章代数式
教学目标
01
理解去括号法则,并熟练运用去括号法则进行运算
02
理解添括号法则,并熟练运用添括号法则进行运算
03
能利用合并同类项和去括号法则进行整式的加减运算
04
掌握整式的加减——化简求值的一般步骤
去括号
从大拇指开始,按食指、中指、无名指、小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5,…。当第四次数到中指时,这个数是几 当第n次数到中指时,这个数是多少 当第200次数到中指时,这个数是多少
01
课堂引入
第一次数到中指时,这个数是3,
第二次数到中指时,这个数是3+5=8,
第三次数到中指时,这个数是3+5×2=13,
01
课堂引入
第四次数到中指时,这个数是3+5×3=18,
…,以此类推,
第n次数到中指时,这个数是3+5×n=5n+3,
第200次数到中指时,这个数是3+5×200=1003。
01
课堂引入
如图,要计算这个图形的面积,
你有几种不同的方法 请计算结果。
法一:将这个图形看作一个大长方形,
则面积为:3(x+3)。
法二:将这个图形看作一个小长方形和一个正方形拼接而成,
则面积为:3x+9。
01
课堂引入
小贴士:代数式中的字母表示的是数,
因此数的运算律也适用于代数式。
用不同方法得到的结果相等,由此你发现了什么
3(x+3)=3x+9
乘法分配律
根据分配律,有:
+(a-b+c)
=1×(a-b+c)
=a-b+c;
02
知识精讲
-a+b-c
=(-1)×(a-b+c)
=-(a-b+c)。
02
知识精讲
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
去括号
eg:+(a-3)=a-3;-(a-3)=-a+3。
一般地,我们有代数式运算的去括号法则:
a-2(3b+2c-2d)如何去括号?
先把括号里的每一项×2,再去括号
把括号里的每一项×(-2)的同时,直接去括号
02
知识精讲
法一:a-2(3b+2c-2d)
=a-(6b+4c-4d)
=a-6b-4c+4d
法二:a-2(3b+2c-2d)
=a-6b-4c+4d
例1-1、去括号:
(1)a+(b+c-d)=________;
(2)a-(b+c)=________;
(3)a-(b-c+d)=________;
(4)a-b-(c-d)=________;
(5)a+b-(-c-d)=________。
a+b+c-d
a-b-c
a-b+c-d
a-b-c+d
a-b+c+d
03
典例精析
例1-2、代数式-[x-(y-z)]去括号后应得( )
A.-x+y-z B.-x-y+z C.-x-y-z D.-x+y+z
【分析】原式=-(x-y+z)=-x+y-z
A
【其他小妙招】x前面1个“-”,即-x;
y前面2个“-”,即y;
z前面3个“-”,即-z。
03
典例精析
例2-1、去括号:
(1)a-2(b+5c)=________________________;
(2)a-3(-3b+2c-d)=________________________。
a-(2b+10c)=a-2b-10c
a-(-9b+6c-3d)=a+9b-6c+3d
先用方法一巩固基础
03
典例精析
例2-2、下列各项去括号正确的是( )
A. -3(m+n)-mn=-3m+3n-mn
B. x2-2(2x-y+2)=x2-4x-2y+4
C. ab-5(-a+3)=ab+5a-3
D. -(5x-3y)+4(2xy-y2)=-5x+3y+8xy-4y2
D
-3m-3n-mn
x2-4x+2y-4
ab+5a-15
总结——常见两类错误:
①符号要变,但没变;
②括号前的系数该乘,但漏乘。
再用方法二提速
03
典例精析
例3、化简:
(1)(x-2y+1)-(2x-y-1); (2)2(2x-3y)-3(x+3y);
解:原式
=x-2y+1-2x+y+1
=(x-2x)+(-2y+y)+(1+1)
=-x-y+2
解:原式
=4x-6y-3x-9y
=(4x-3x)+(-6y-9y)
=x-15y
03
典例精析
(3)-3(a-2b-3)-5(a+b-1); (4)6a2-2[5a-(2a2-a)+a2]。
解:原式
=-3a+6b+9-5a-5b+5
03
典例精析
=(-3a-5a)+(6b-5b)+(9+5)
=-8a+b+14
解:原式
=6a2-2(5a-2a2+a+a2)
=6a2-2(6a-a2)
=6a2-12a+2a2
=(6a2+2a2)-12a
=8a2-12a
例4、化简:3(a+b)-7(a+b)-5(x+y)+9(x+y)。
先将(a+b)、(x+y)看作整体,合并同类项,再去括号
解:原式
=-4(a+b)+4(x+y)
=-4a-4b+4x+4y
03
典例精析
例5、求(3x2+xy+2y)-2(5xy-4x2+y)的值,其中x=-1,y=-。
解:(3x2+xy+2y)-2(5xy-4x2+y)
=3x2+xy+2y-10xy+8x2-2y
=(3x2+8x2)+(xy-10xy)+(2y-2y)
=11x2-9xy,
03
典例精析
先化简
后求值
当x=-1,y=-时,原式=11×(-1)2-9×(-1)×(-)=11-3=8。
添括号
已知+(a-b+c)=a-b+c,-(a-b+c)=-a+b-c,这两个等式从左到右看是去括号,原理是乘法分配律,那么从右往左看呢?
从右往左看是添括号,原理是乘法分配律的逆用。
01
课堂引入
将两个式子左右颠倒:
a-b+c=+(a-b+c);-a+b-c=-(a-b+c)。
02
知识精讲
添括号法则:
添加括号和“+”号,括号里各项都不变号;
添加括号和“-”号,括号里各项都改变符号。
添括号
eg:a-3=+(a-3);-a+3=-(a-3)。
别忘了再从右往左看,检验结果的正确性哦!
例1、填空:
(1)x+y-z=x+( );
(2)x-y-z=x-( );
(3)3a-2b+7c=3a-( );
(4)-2x2+y-z-5=-(2x2+5)-( )。
y-z
y+z
2b-7c
-y+z
03
典例精析
例2、下列添括号正确的是( )
A. -b-c=-(b-c)
B. -2x+6y=-2(x-6y)
C. a-b=+(a-b)
D. x-y-1=x-(y-1)
C
-(b+c)
-2(x-3y)
x-y+1
03
典例精析
例3、填空:
不改变多项式3b3-2ab2+4a2b-6a3的值,把后三项放在前面是“-”号的括号中,则3b3-2ab2+4a2b-6a3=3b3-2( )。
ab2-2a2b+3a3
03
典例精析
整式的加减
如图,甲、乙两个零件截面的面积哪一个较大 大多少 把结果填在下面的横线上。
截面甲的面积是________________,
截面乙的面积是________________,
甲、乙两个截面面积的差是
(________)-(________)。
01
课堂引入
πr2-2ab
πr2-1.5ab
πr2-2ab
πr2-1.5ab
(πr2-2ab)-(πr2-1.5ab)
=πr2-2ab-πr2+1.5ab
=-0.5ab
去括号
合并同类项
02
知识精讲
整式的加减可以归结为去括号与合并同类项。
整式的加减
在解决实际问题时,经常需要把若干个整式相加减。
【尝试】求5a2-7a+2与-3a2+2a-1的差。
02
知识精讲
解:5a2-7a+2-(-3a2+2a-1)
=5a2-7a+2+3a2-2a+1
=8a2-9a+3。
例1、已知A-2B=8a2-7ab,B=-4a2+6ab+7,求多项式A。
解:∵A-2B=8a2-7ab,B=-4a2+6ab+7,
∴A=2B+8a2-7ab
=2(-4a2+6ab+7)+8a2-7ab
=-8a2+12ab+14+8a2-7ab
=5ab+14。
03
典例精析
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
解:法一:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
=-2x2+x-1-2x2+4x-5
=-4x2+5x-6,
03
典例精析
A-(2x2-4x+5)
=-4x2+5x-6-(2x2-4x+5)
=-4x2+5x-6-2x2+4x-5
=-6x2+9x-11。
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
法二:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
∴A-(2x2-4x+5)
=-2x2+x-1-2(2x2-4x+5)
=-2x2+x-1-4x2+8x-10
=-6x2+9x-11。
03
典例精析
整式的化简求值
例1、已知M=3a2+4ab-1,N=a2-2ab-1,
(1)用含a、b的代数式表示M-3N;
(2)若a、b满足(a-1)2+|b-2|=0,求M-3N的值。
03
典例精析
解:(1)M-3N
=3a2+4ab-1-3(a2-2ab-1)
=3a2+4ab-1-3a2+6ab+3
=10ab+2;
(2)∵(a-1)2+|b-2|=0,
∴a=1,b=2,
∴M-3N=10ab+2=10×1×2+2=22。
03
典例精析
【题型】整式的加减——化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将字母表示的数代入化简后的式子计算。
例2、先化简,再求值:已知8x2ay与-3x4y2+b是同类项,且A=a2+ab-2b2,B=3a2-ab-6b2,求2B-3(B-A)的值。
∵8x2ay与-3x4y2+b是同类项,
∴2a=4,1=2+b,
∴a=2,b=-1,
∴2B-3(B-A)=4ab=4×2×(-1)=-8。
解:2B-3(B-A)
=2B-3B+3A
=3A-B
=3(a2+ab-2b2)-(3a2-ab-6b2)
=3a2+3ab-6b2-3a2+ab+6b2
=4ab;
03
典例精析
课后总结
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
符号语言:+(a-b+c)=a-b+c;-(a-b+c)=-a+b-c。
添括号法则:
添加括号和“+”号,括号里各项都不变号;
添加括号和“-”号,括号里各项都改变符号。
符号语言:a-b+c=+(a-b+c);-a+b-c=-(a-b+c)。
课后总结
整式的加减可以归结为去括号与合并同类项。
【题型】整式的加减——化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将字母表示的数代入化简后的式子计算。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
