浙江省丽水市庆元县岭头乡中心学校浙教版九年级数学下册课件:2.2 切线长定理(共11张PPT)
文档属性
| 名称 | 浙江省丽水市庆元县岭头乡中心学校浙教版九年级数学下册课件:2.2 切线长定理(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 207.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-07 00:00:00 | ||
图片预览

文档简介
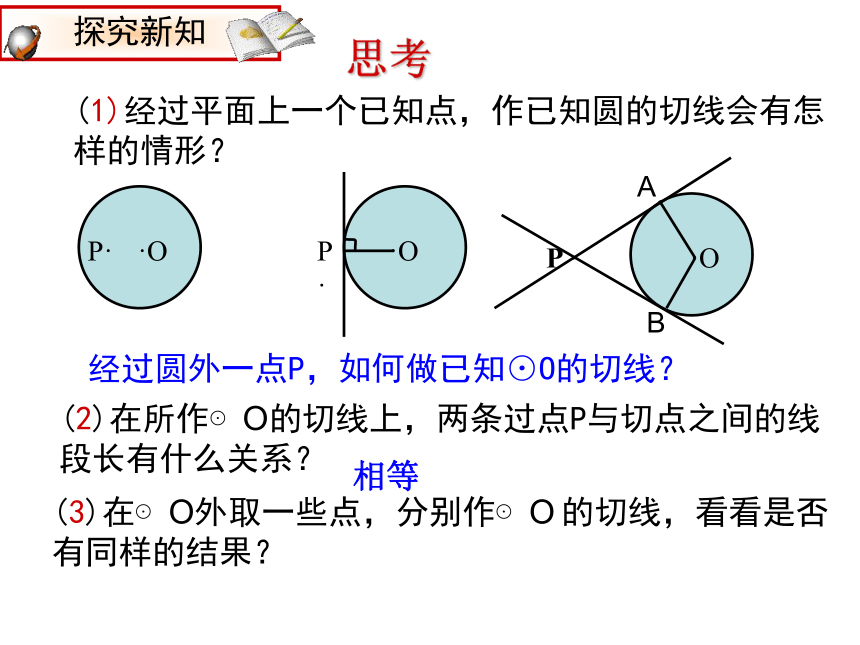
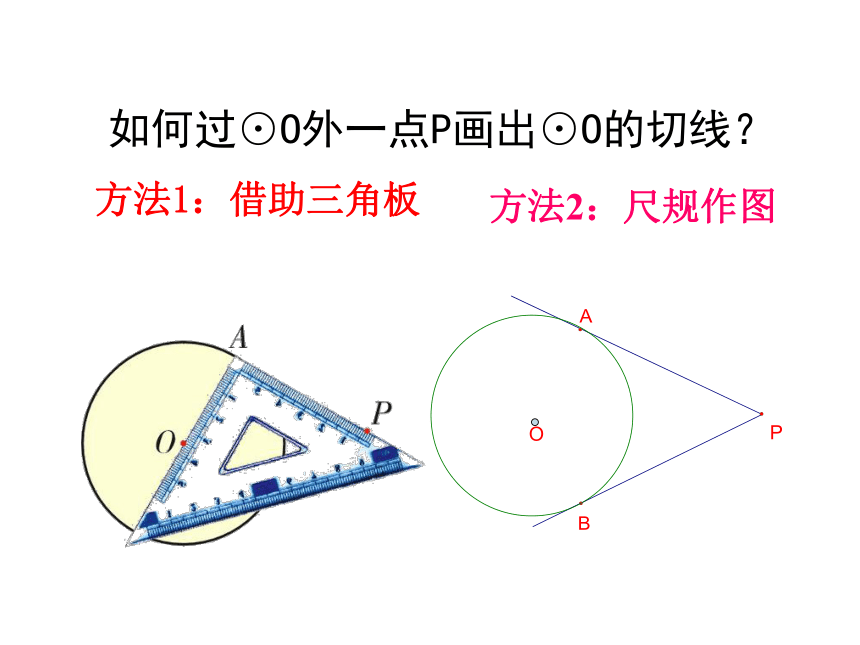
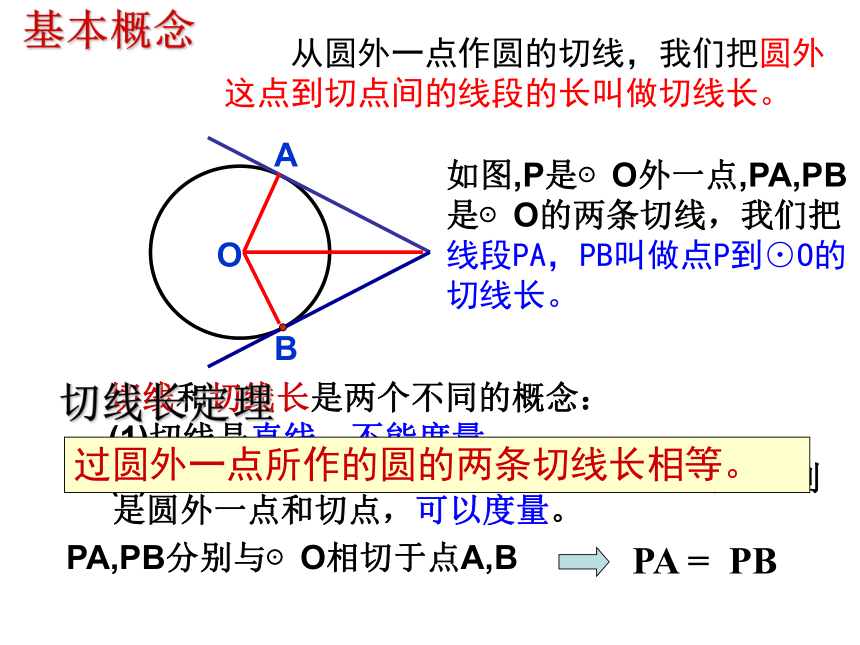
课件11张PPT。2.2切线长定理(1)经过平面上一个已知点,作已知圆的切线会有怎样的情形?P ·P·P ·经过圆外一点P,如何做已知⊙O的切线?AB思考(2)在所作⊙O的切线上,两条过点P与切点之间的线段长有什么关系?相等(3)在⊙O外取一些点,分别作⊙O 的切线,看看是否有同样的结果? 如何过⊙O外一点P画出⊙O的切线?方法1:借助三角板方法2:尺规作图如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB叫做点P到⊙O的切线长。 从圆外一点作圆的切线,我们把圆外这点到切点间的线段的长叫做切线长。 切线和切线长是两个不同的概念:
(1)切线是直线,不能度量;
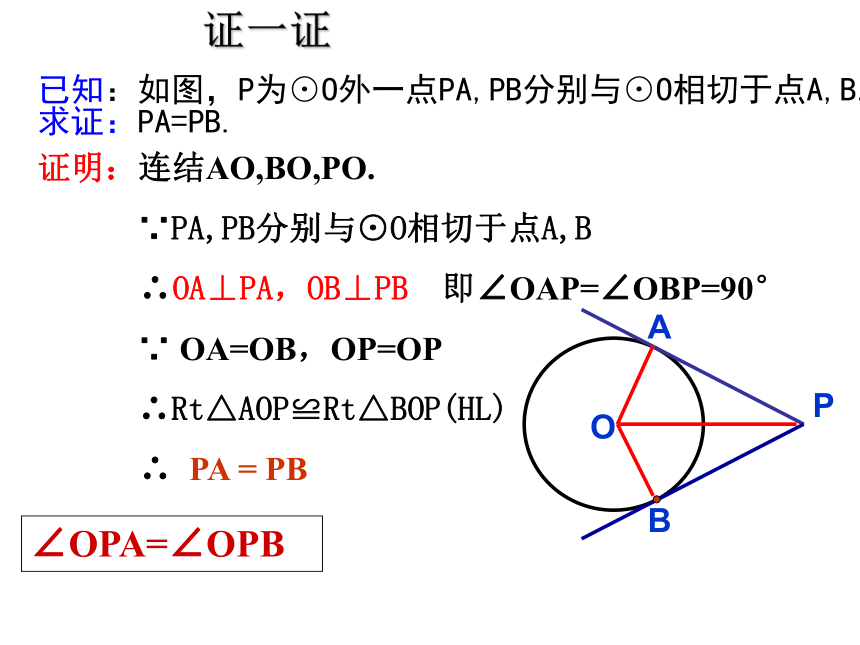
(2)切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。基本概念过圆外一点所作的圆的两条切线长相等。切线长定理PA,PB分别与⊙O相切于点A,BPA = PB已知:如图,P为⊙O外一点PA,PB分别与⊙O相切于点A,B.求证:PA=PB.P证明:连结AO,BO,PO.
∵PA,PB分别与⊙O相切于点A,B
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB证一证∠OPA=∠OPB例1 如图,在⊙O中,AC,BC分别与⊙O相切于点A,B.已知∠ACB=800,OC=100cm.求点C到⊙O的切线长(结果精确到1cm).CBOA例2 如图,⊙O表示皮带传动装置的一个轮子,传动皮带MA,NB分别切⊙O于点A,B.延长MA,NB,相交于点P.已知∠APB=600,AP=24cm,求两切点间的距离和弧AB的长(精确到1cm).MNMNMN1.已知⊙O的半径为5,P是⊙O外一点,PO=10,求点P到⊙O的切线长和两切点间的劣弧长。 OABMN2.已知:在⊙O中,弦AB垂直平分半径ON,过点A,B的切线相交于点M.求证△ABM为等边三角形.课内练习1、已知:在⊙O中,PA、PB分别为⊙O的切线,A、B为切点,已知⊙O的半径为1 ,OP=2.4,求切线长。(精确到0.1)和∠APB的度数。PBOA作业题完成作业题2、3、51.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。BAP课堂小结。PBAO(3)连结圆心和圆外一点(2)连结两切点(1)分别连结圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形,添加辅助线。归纳反思
(1)切线是直线,不能度量;
(2)切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。基本概念过圆外一点所作的圆的两条切线长相等。切线长定理PA,PB分别与⊙O相切于点A,BPA = PB已知:如图,P为⊙O外一点PA,PB分别与⊙O相切于点A,B.求证:PA=PB.P证明:连结AO,BO,PO.
∵PA,PB分别与⊙O相切于点A,B
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB证一证∠OPA=∠OPB例1 如图,在⊙O中,AC,BC分别与⊙O相切于点A,B.已知∠ACB=800,OC=100cm.求点C到⊙O的切线长(结果精确到1cm).CBOA例2 如图,⊙O表示皮带传动装置的一个轮子,传动皮带MA,NB分别切⊙O于点A,B.延长MA,NB,相交于点P.已知∠APB=600,AP=24cm,求两切点间的距离和弧AB的长(精确到1cm).MNMNMN1.已知⊙O的半径为5,P是⊙O外一点,PO=10,求点P到⊙O的切线长和两切点间的劣弧长。 OABMN2.已知:在⊙O中,弦AB垂直平分半径ON,过点A,B的切线相交于点M.求证△ABM为等边三角形.课内练习1、已知:在⊙O中,PA、PB分别为⊙O的切线,A、B为切点,已知⊙O的半径为1 ,OP=2.4,求切线长。(精确到0.1)和∠APB的度数。PBOA作业题完成作业题2、3、51.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。BAP课堂小结。PBAO(3)连结圆心和圆外一点(2)连结两切点(1)分别连结圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形,添加辅助线。归纳反思
