浙教版八年级数学下册4.5三角形的中位线课件(共22张PPT)
文档属性
| 名称 | 浙教版八年级数学下册4.5三角形的中位线课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 513.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-15 09:59:13 | ||
图片预览







文档简介
课件22张PPT。教学活动一:
创设情境,导入概念ABCDE 问题:A、B两点被池塘隔开,现在要测量出A、B两点间的距离,但又无法直接去测量,怎么办?在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。这样做的道理是什么? 今天这堂课我们就要来探究其中的学问。DEDE是三角形ABC的中位线三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。画出三角形的所有中线并说出中位线和中线的区别.DEF教学活动二:
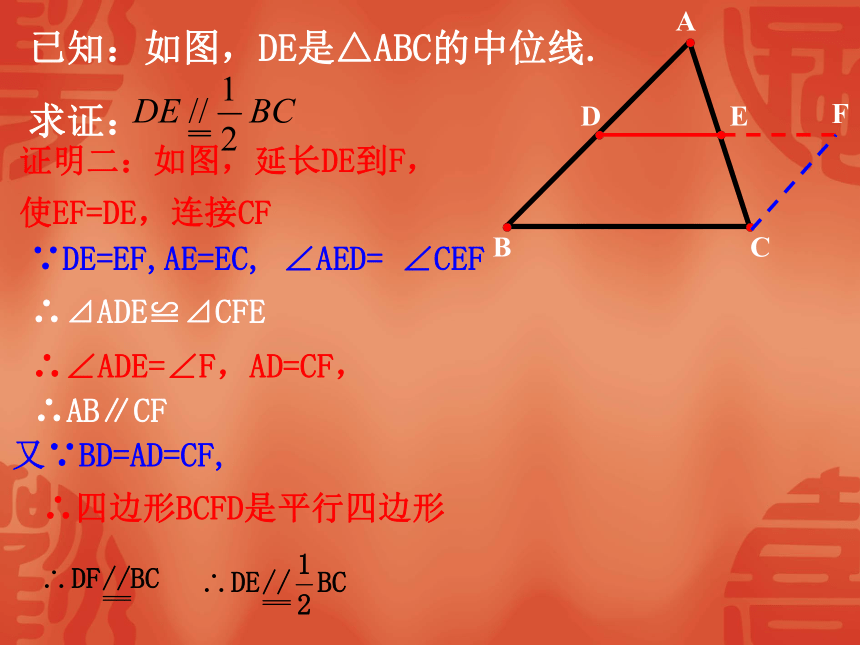
合作交流,探究新知ABCDE三角形的中位线与第三边有什么关系? 三角形的中位线平行且等于第三边的一半结论:三角形的中位线平行于第三边,并且等于它的一半.证明:如图,以点E为旋转中心,把⊿ADE绕点E,按顺时针方向旋转180゜,得到⊿CFE ABCDEF得到⊿CFE,⊿ADE≌⊿CFE.∴∠ADE=∠F,AD=CF,DE=EF∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形证明命题:三角形的中位线平行且等于第三边的一半证明二:如图,延长DE到F,使EF=DE,连接CF∴∠ADE=∠F,AD=CF,∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形 ABCDEF∵DE=EF,AE=EC, ∠AED= ∠CEF∴⊿ADE≌⊿CFEABCEDF证法三:延长DE到点F,使EF=DE, 连结AF、CF、CD
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形 ∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形?ABCDEB、三角形的中位线定理三角形的中位线与第三边有什么关系? 三角形的中位线平行且等于第三边的一半数学活动三:
体验三角形中位线的应用价值,
提高发散思维水平和能力 学生练习1:如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点。
求证:∠PNM=∠PMN。学生练习2、如图,已知矩形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点.当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是( ).
(A)线段EF的长逐渐增大 (B)线段EF的长逐渐减少
(C)线段EF的长不变 (D)线段EF的长不能确定 学生练习3:如图,在△ABC中,CF平分∠ACB,CA=CD,AE=EB,则EF与BD有怎样的关系?学生练习5:已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN。D,E,F分别是MB,BC,CN的中点,连结DE,EF。
求证:DE=EF数学活动四:
例题与拓展例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
(1)?顺次连结平行四边形各边中点所得的四边形是什么?(2)顺次连结菱形各边中点所得的四边形是什么?平行四边形矩形 (3)顺次连结正方形各边中点所得的四边形是什么? 正方形(4)顺次连结梯形各边中点所得的四边形是什么?(5)顺次连结等腰梯形各边中点所得的四边形是什么?平行四边形菱形 顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?议一议拓展 (6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么? (7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?菱形矩形正方形教学活动五:
小结与反思
创设情境,导入概念ABCDE 问题:A、B两点被池塘隔开,现在要测量出A、B两点间的距离,但又无法直接去测量,怎么办?在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。这样做的道理是什么? 今天这堂课我们就要来探究其中的学问。DEDE是三角形ABC的中位线三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。画出三角形的所有中线并说出中位线和中线的区别.DEF教学活动二:
合作交流,探究新知ABCDE三角形的中位线与第三边有什么关系? 三角形的中位线平行且等于第三边的一半结论:三角形的中位线平行于第三边,并且等于它的一半.证明:如图,以点E为旋转中心,把⊿ADE绕点E,按顺时针方向旋转180゜,得到⊿CFE ABCDEF得到⊿CFE,⊿ADE≌⊿CFE.∴∠ADE=∠F,AD=CF,DE=EF∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形证明命题:三角形的中位线平行且等于第三边的一半证明二:如图,延长DE到F,使EF=DE,连接CF∴∠ADE=∠F,AD=CF,∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形 ABCDEF∵DE=EF,AE=EC, ∠AED= ∠CEF∴⊿ADE≌⊿CFEABCEDF证法三:延长DE到点F,使EF=DE, 连结AF、CF、CD
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形 ∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形?ABCDEB、三角形的中位线定理三角形的中位线与第三边有什么关系? 三角形的中位线平行且等于第三边的一半数学活动三:
体验三角形中位线的应用价值,
提高发散思维水平和能力 学生练习1:如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点。
求证:∠PNM=∠PMN。学生练习2、如图,已知矩形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点.当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是( ).
(A)线段EF的长逐渐增大 (B)线段EF的长逐渐减少
(C)线段EF的长不变 (D)线段EF的长不能确定 学生练习3:如图,在△ABC中,CF平分∠ACB,CA=CD,AE=EB,则EF与BD有怎样的关系?学生练习5:已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN。D,E,F分别是MB,BC,CN的中点,连结DE,EF。
求证:DE=EF数学活动四:
例题与拓展例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
(1)?顺次连结平行四边形各边中点所得的四边形是什么?(2)顺次连结菱形各边中点所得的四边形是什么?平行四边形矩形 (3)顺次连结正方形各边中点所得的四边形是什么? 正方形(4)顺次连结梯形各边中点所得的四边形是什么?(5)顺次连结等腰梯形各边中点所得的四边形是什么?平行四边形菱形 顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?议一议拓展 (6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么? (7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?菱形矩形正方形教学活动五:
小结与反思
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
