2.1 一元二次方程 教学设计(表格式)2024-2025学年浙教版数学八年级下册
文档属性
| 名称 | 2.1 一元二次方程 教学设计(表格式)2024-2025学年浙教版数学八年级下册 | 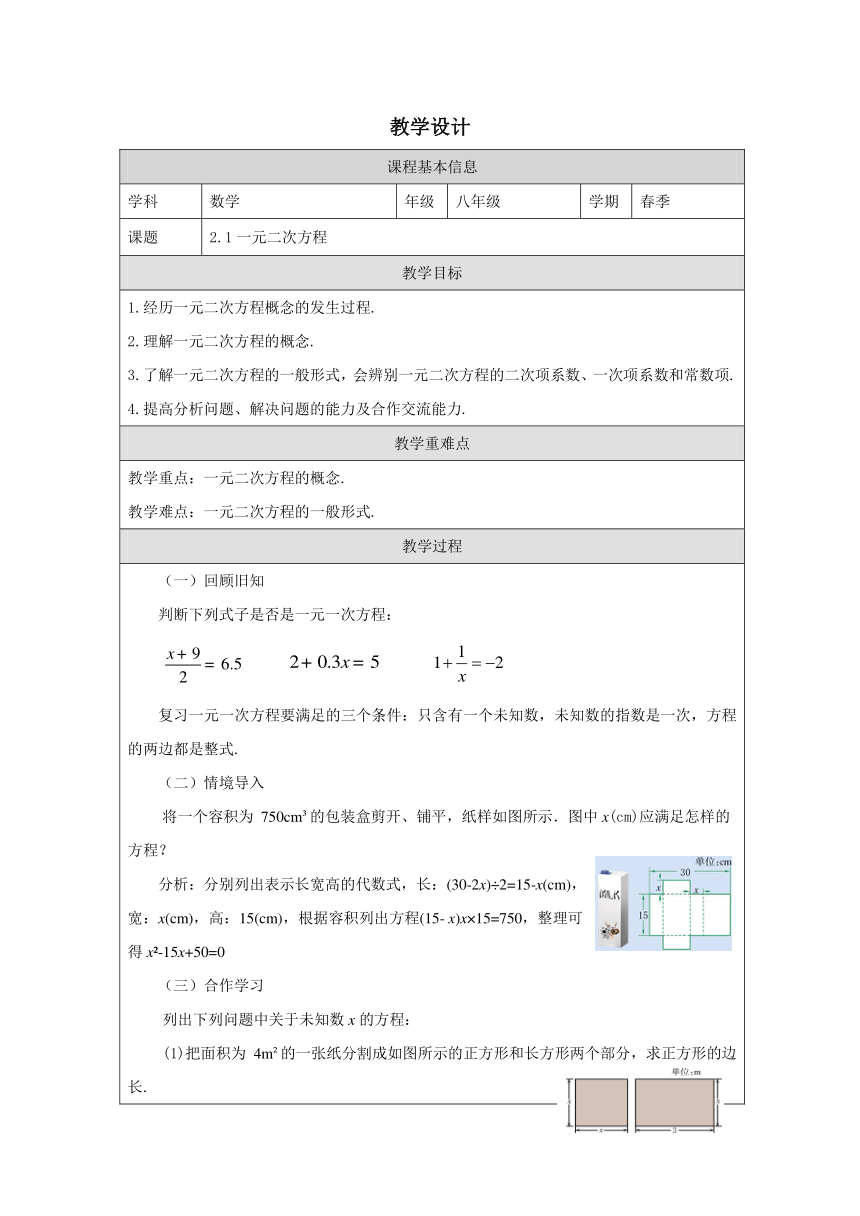 | |
| 格式 | docx | ||
| 文件大小 | 138.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-17 13:29:25 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 2.1一元二次方程
教学目标
1.经历一元二次方程概念的发生过程. 2.理解一元二次方程的概念. 3.了解一元二次方程的一般形式,会辨别一元二次方程的二次项系数、一次项系数和常数项. 4.提高分析问题、解决问题的能力及合作交流能力.
教学重难点
教学重点:一元二次方程的概念.
教学难点:一元二次方程的一般形式.
教学过程
(一)回顾旧知 判断下列式子是否是一元一次方程: 复习一元一次方程要满足的三个条件:只含有一个未知数,未知数的指数是一次,方程的两边都是整式. 情境导入 将一个容积为 750cm 的包装盒剪开、铺平,纸样如图所示.图中x(cm)应满足怎样的方程? 分析:分别列出表示长宽高的代数式,长:(30-2x)÷2=15-x(cm), 宽:x(cm),高:15(cm),根据容积列出方程(15- x)x×15=750,整理可 得x -15x+50=0 合作学习 列出下列问题中关于未知数x的方程: (1)把面积为4m 的一张纸分割成如图所示的正方形和长方形两个部分,求正方形的边长. 设正方形的边长为x(m),可列出方程 x +3x=4 . (2)某放射性元素经2天后,质量衰变为原来的,这种放射性元素平均每天减少率为多少? 设平均每天减少率为x ,可列出方程: . 探究新知 思考:观察x -15x+50=0、x +3x=4、 这三个方程,说出这些方程与一元一次 方程的相同和不同之处. 相同之处:只含有一个未知数,方程的两边都是整式. 不同之处:一元一次方程所含未知数的最高次数为1次,上述三个方程所含未知数的最高次数为2次. 概念形成 方程x -15x+50=0、x +3x=4、 的两边都是整式,只含有一个未知数,并且未 知数的最高次数是2次.我们把这样的方程叫做一元二次方程. 能使一元二次方程两边相等的未知数的值叫做一元二次方程的解(或根). 新知应用 1.判断下列方程是否为一元二次方程: (1) 10x =9 ( ) (2) 2(x-1)=3x ( ) (3) 2x -3x-1=0 ( ) (4) ( ) 归纳一元二次方程满足的三个条件:只含有一个未知数,未知数的最高次数是二次,方程的两边都是整式. 2.判断未知数的值x=-1,x=0,x=2是不是方程x -2=x的根? 分析:要判断一个未知数的值是不是方程的根,只需将未知数的值分别代入方程的左边和方程的右边. 解:当x=-1时, 左边= 2=( 1) 2=1 2= 1 右边=x= 1 ∴左边=右边 ∴x=-1是原方程的解 同理可得:x=2是原方程的解, x=0不是原方程的解. 归纳:一般的对于任何一个关于x的一元二次方程,都可以化成ax +bx+c=0(a,b,c为常数,a≠0),这种形式称为一元二次方程的一般形式.其中ax ,bx,c分别称为二次项,一次项和常数项,a叫做二次项系数,b叫做一次项系数. 思考:为什么a≠0?b,c可以为零吗?如果a=0,则这个方程就变为bx+c=0,那么它就不包含二次项,就不是一元二次方程. b和c是可以为零的,因为无论是b=0还是c=0,这个方程的一般形式仍然符合一元二次方程的三个条件,所以它还是一个一元二次方程. 因此在解答一元二次方程的问题时一定要特别注意,二次项系数不能为零. 例题演练 例1.把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项. 9x =5-4x. (2) (2-x)(3x+4)=3. 解:(1) 移项,整理,得9x +4x-5=0. 这个方程的二次项系数是9,一次项系数是4,常数项是-5. (2)方程左边多项式相乘,得-3x +2x+8=3, 移项,整理,得-3x +2x+5=0. 这个方程的二次项系数是-3,一次项系数是2,常数项是5. 例2.已知一元二次方程2x + bx+c=0的两个根为和,求这个方程. 解:将和代入方程2x + bx+c=0,得 解得所以这个一元二次方程是2x +x-15=0. 在这里要特别注意,我们写一元二次方程的一般形式的时候,通常按未知数的次数从高到低写,也就是先写二次项,再写一次项,最后写常数项。 变式练习 把化成一元二次方程的一般形式,并写出它的二次项系数、一次项 系数和常数项. 所以这个方程的二次项系数是3,一次项系数是-14,常数项是9. (九)深化拓展 1.已知关于x的一元二次方程x +ax+a=0的一个根是3,求a的值. 解:把x=3代入方程x +ax+a=0中,得:9+3a+a=0,∴a= . 2.已知关于x的方程的一个解是x=0,则m的值是多少?该方程是否为一元二次方程? 解:由题意得:m -1=0,∴m=±1. 当m=1时,这是一元一次方程,当m=-1时,这是一元二次方程. 在这道题目中我们用到了分类讨论思想,也就是原题条件给我们的是一个方程,并没有指明是什么方程时,我们需要对方程中的其他参数进行讨论,也就是它必须满足方程的所有条件,它才能是一个一元二次方程。 (十)课堂小结
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 2.1一元二次方程
教学目标
1.经历一元二次方程概念的发生过程. 2.理解一元二次方程的概念. 3.了解一元二次方程的一般形式,会辨别一元二次方程的二次项系数、一次项系数和常数项. 4.提高分析问题、解决问题的能力及合作交流能力.
教学重难点
教学重点:一元二次方程的概念.
教学难点:一元二次方程的一般形式.
教学过程
(一)回顾旧知 判断下列式子是否是一元一次方程: 复习一元一次方程要满足的三个条件:只含有一个未知数,未知数的指数是一次,方程的两边都是整式. 情境导入 将一个容积为 750cm 的包装盒剪开、铺平,纸样如图所示.图中x(cm)应满足怎样的方程? 分析:分别列出表示长宽高的代数式,长:(30-2x)÷2=15-x(cm), 宽:x(cm),高:15(cm),根据容积列出方程(15- x)x×15=750,整理可 得x -15x+50=0 合作学习 列出下列问题中关于未知数x的方程: (1)把面积为4m 的一张纸分割成如图所示的正方形和长方形两个部分,求正方形的边长. 设正方形的边长为x(m),可列出方程 x +3x=4 . (2)某放射性元素经2天后,质量衰变为原来的,这种放射性元素平均每天减少率为多少? 设平均每天减少率为x ,可列出方程: . 探究新知 思考:观察x -15x+50=0、x +3x=4、 这三个方程,说出这些方程与一元一次 方程的相同和不同之处. 相同之处:只含有一个未知数,方程的两边都是整式. 不同之处:一元一次方程所含未知数的最高次数为1次,上述三个方程所含未知数的最高次数为2次. 概念形成 方程x -15x+50=0、x +3x=4、 的两边都是整式,只含有一个未知数,并且未 知数的最高次数是2次.我们把这样的方程叫做一元二次方程. 能使一元二次方程两边相等的未知数的值叫做一元二次方程的解(或根). 新知应用 1.判断下列方程是否为一元二次方程: (1) 10x =9 ( ) (2) 2(x-1)=3x ( ) (3) 2x -3x-1=0 ( ) (4) ( ) 归纳一元二次方程满足的三个条件:只含有一个未知数,未知数的最高次数是二次,方程的两边都是整式. 2.判断未知数的值x=-1,x=0,x=2是不是方程x -2=x的根? 分析:要判断一个未知数的值是不是方程的根,只需将未知数的值分别代入方程的左边和方程的右边. 解:当x=-1时, 左边= 2=( 1) 2=1 2= 1 右边=x= 1 ∴左边=右边 ∴x=-1是原方程的解 同理可得:x=2是原方程的解, x=0不是原方程的解. 归纳:一般的对于任何一个关于x的一元二次方程,都可以化成ax +bx+c=0(a,b,c为常数,a≠0),这种形式称为一元二次方程的一般形式.其中ax ,bx,c分别称为二次项,一次项和常数项,a叫做二次项系数,b叫做一次项系数. 思考:为什么a≠0?b,c可以为零吗?如果a=0,则这个方程就变为bx+c=0,那么它就不包含二次项,就不是一元二次方程. b和c是可以为零的,因为无论是b=0还是c=0,这个方程的一般形式仍然符合一元二次方程的三个条件,所以它还是一个一元二次方程. 因此在解答一元二次方程的问题时一定要特别注意,二次项系数不能为零. 例题演练 例1.把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项. 9x =5-4x. (2) (2-x)(3x+4)=3. 解:(1) 移项,整理,得9x +4x-5=0. 这个方程的二次项系数是9,一次项系数是4,常数项是-5. (2)方程左边多项式相乘,得-3x +2x+8=3, 移项,整理,得-3x +2x+5=0. 这个方程的二次项系数是-3,一次项系数是2,常数项是5. 例2.已知一元二次方程2x + bx+c=0的两个根为和,求这个方程. 解:将和代入方程2x + bx+c=0,得 解得所以这个一元二次方程是2x +x-15=0. 在这里要特别注意,我们写一元二次方程的一般形式的时候,通常按未知数的次数从高到低写,也就是先写二次项,再写一次项,最后写常数项。 变式练习 把化成一元二次方程的一般形式,并写出它的二次项系数、一次项 系数和常数项. 所以这个方程的二次项系数是3,一次项系数是-14,常数项是9. (九)深化拓展 1.已知关于x的一元二次方程x +ax+a=0的一个根是3,求a的值. 解:把x=3代入方程x +ax+a=0中,得:9+3a+a=0,∴a= . 2.已知关于x的方程的一个解是x=0,则m的值是多少?该方程是否为一元二次方程? 解:由题意得:m -1=0,∴m=±1. 当m=1时,这是一元一次方程,当m=-1时,这是一元二次方程. 在这道题目中我们用到了分类讨论思想,也就是原题条件给我们的是一个方程,并没有指明是什么方程时,我们需要对方程中的其他参数进行讨论,也就是它必须满足方程的所有条件,它才能是一个一元二次方程。 (十)课堂小结
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
