4.2 相似三角形

课件17张PPT。相似三角形相似三角形相似三角形的概念
相似三角形的基本性质
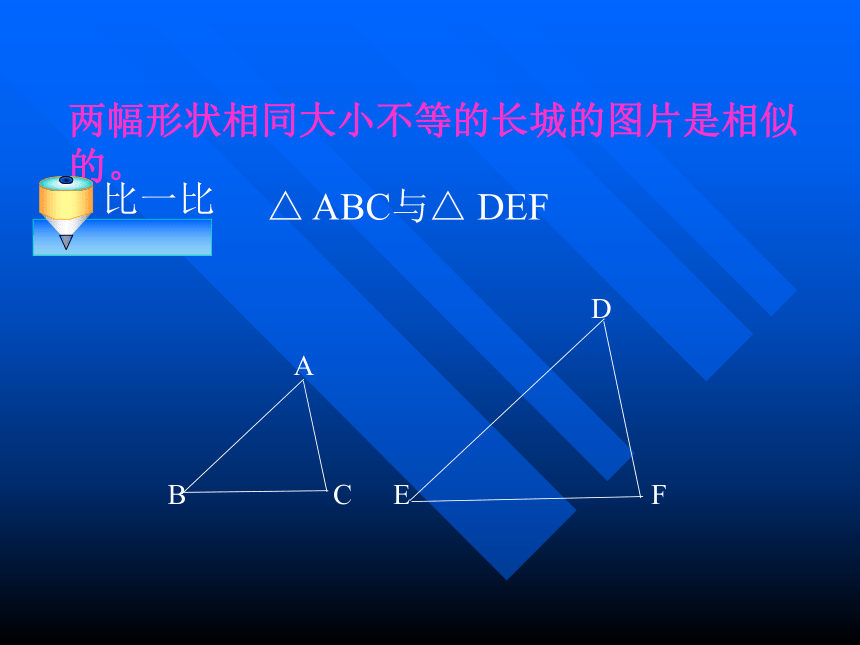
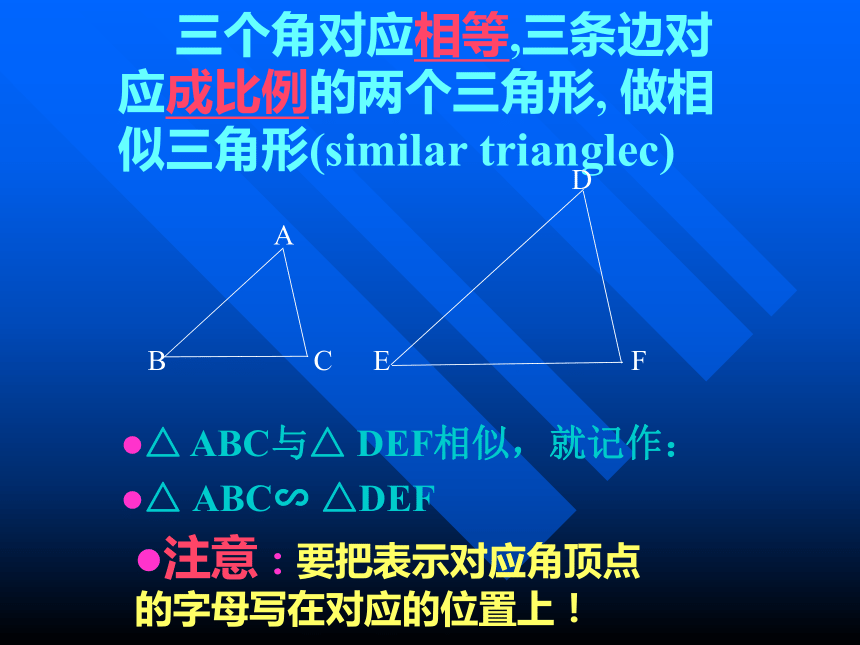
相似三角形的预备定理两幅形状相同大小不等的长城的图片是相似的。△ ABC与△ DEF 三个角对应相等,三条边对应成比例的两个三角形, 做相似三角形(similar trianglec)
△ ABC与△ DEF相似，就记作：
△ ABC∽ △DEF
注意：要把表示对应角顶点的字母写在对应的位置上！
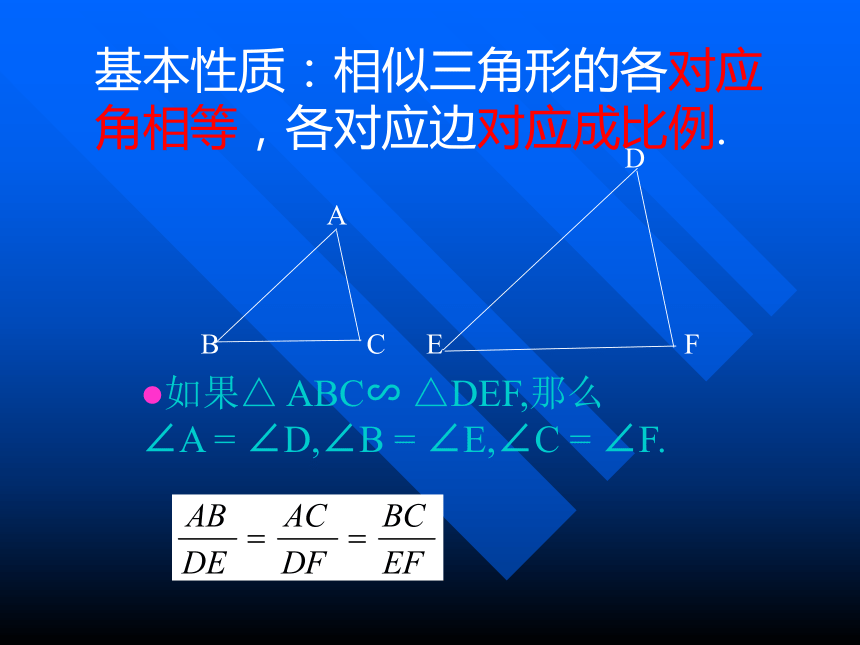
基本性质：相似三角形的各对应角相等，各对应边对应成比例.如果△ ABC∽ △DEF,那么
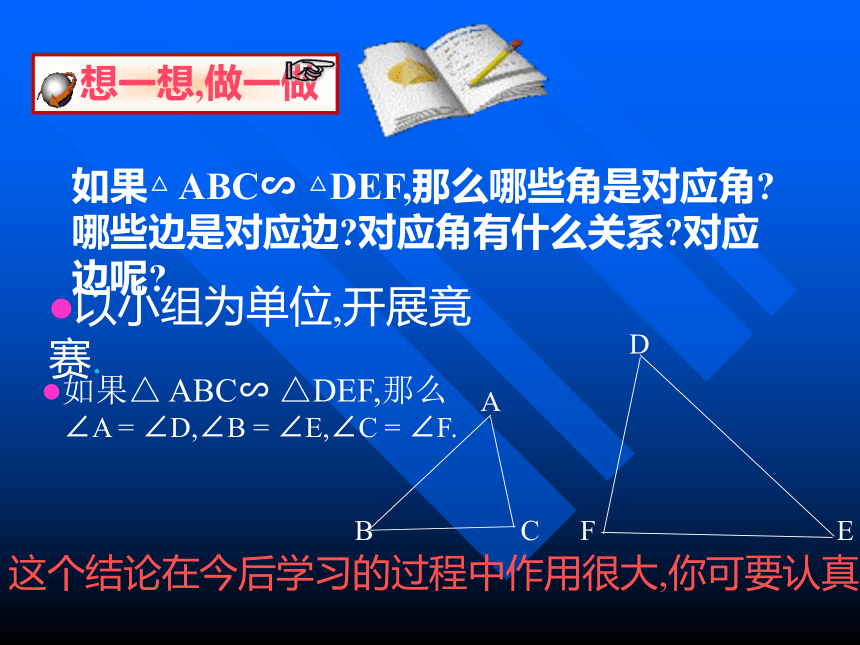
∠A = ∠D,∠B = ∠E,∠C = ∠F.如果△ ABC∽ △DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢?以小组为单位,开展竟赛.如果△ ABC∽ △DEF,那么
∠A = ∠D,∠B = ∠E,∠C = ∠F.这个结论在今后学习的过程中作用很大,你可要认真噢！１、两个全等三角形一定相似吗？为什么？２.两个直角三角形一定相似吗？为什么？两个等腰直角三角形呢？３.两个等腰三角形一定相似吗？为什么？两个等边三角形呢？ 1.相似.因为对应角相等,对应边成比例.２.两个直角三角形不一定相似.因为对应角不一定相等,对应边也不一定成比例;两个等腰直角三角形相似.因为对应角相等,对应边成比例.３.两个等腰三角形不一定相似;
两个等边三角形相似.交流讨论你注意到没有,相似三角形的各对应角相等，各对应边对应成比例.在解题时的作用了吗?1、在下面的两组图形中,各有两个相似三角形,试确定x ,y ,m ,n 的值. 你准备如何去做?
X=32,y=20/3,m=800,n=550.如图，已知DE ∥ BC
则．．．．．．故△ADE∽ △ABC,若△ABC∽ △DEC,从上面的解答中，你获得了那些信息？ 平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。相似三角形的预备定理这是两个极具代表性的
相似三角形基本模型：“A”型和“X” 型这个两个模型在今后学习的过程中作用很大,你可要认真噢！看过例题过后，你又有什么收获？例１、如图，有一块呈三角形形状的草坪，其中一边的长是20m，在这个草坪的图纸上，这条边长5cm，其他两边的长度都是3.5cm。求该草坪其他两边的实际长度。解: 草坪的实际形状和它在图纸上相应的形状相似.所以实际的三角形与图上的三角形相似,且它们的相似比2000:5= 400:1.如果设其它两边的实际长度都是xcm,那么X=3.5×400=1400(cm),
1400cm=14m.
所以,草坪其它两边的实际长度都是14m.例2、如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
解: 因为DE ∥ BC ，所以△ADE∽△ABC,
(1)由相似三角形对应角相等,得∠AED=∠C=400.
在△ADE中, ∠ADE=1800-400-450=950.（2）由相似三角形对应边成比例。得三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形(similar trianglec).
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上！
性质：相似三角形的各对应角相等,各对应边对应成比例.
如果△ ABC∽ △DEF,那么∠A = ∠D,∠B = ∠E,∠C = ∠F.预备定理 平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。 想一想,相似比等于1的两个三角形会是什么样的关系？ 如图，分别根据下列已知条件和刚学得知识，试写出你能得出的结论。我思，我进步（1） DE ∥ BC；（1）（2）DE ∥AB；
（3）△ABC∽△ADE，其中∠ADE = ∠B（2）（3）知识的升华习题5.3
2,10题.结束寄语不经历风雨，怎么见彩虹.,没有人能随随便便成功!