第五章 一元一次方程 章末复习----字母系数---待确定的数 课件(共15张PPT)
文档属性
| 名称 | 第五章 一元一次方程 章末复习----字母系数---待确定的数 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
浙教版七年级上册
第五章 一元一次方程章末复习
-------字母系数:待确定的数
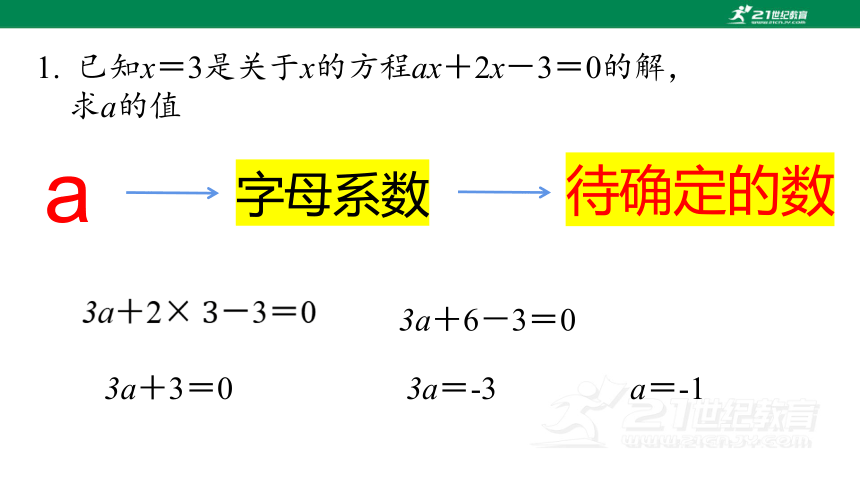
1. 已知x=3是关于x的方程ax+2x-3=0的解,
求a的值
a
字母系数
待确定的数
3a+2-3=0
3a+6-3=0
3a+3=0
3a=-3
a=-1
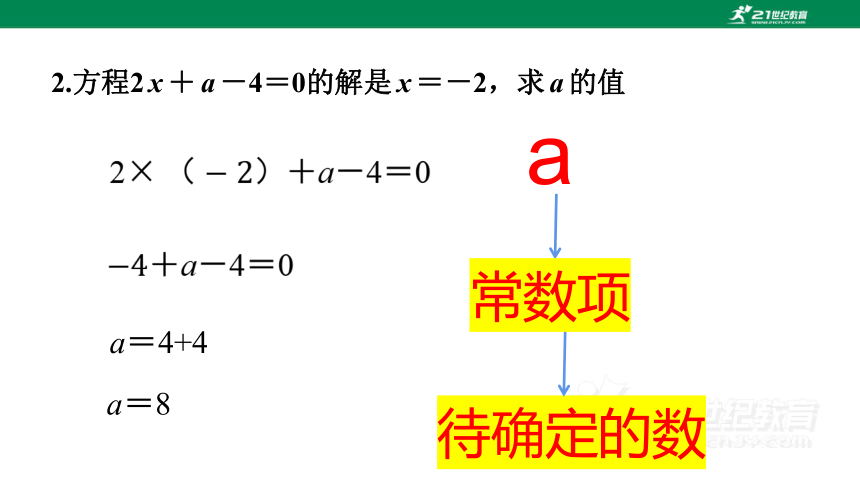
2.方程2 x + a -4=0的解是 x =-2,求 a 的值
2+a-4=0
+a-4=0
a=4+4
a=8
a
待确定的数
常数项
3.如果方程和方程
的解相同, 的值
4. 已知关于 x 的方程9 x -3= kx +14有整数解,
求满足条件的整数 k .
解:原方程得 x = ,
当9- k =-1时, k =10;
当9- k =1时, k =8;
当9- k =17时, k =-8;
当9- k =-17时, k =26.
综上,满足条件的整数 k =10或8或-8或26.
17=1
5. 解关于 x 的方程:2 ax +2=12 x +3 b .
【解】把方程2 ax +2=12 x +3 b 变形,
得(2 a -12) x =3 b -2.
分三种情况:
(1)当2 a -12≠0,即 a ≠6时,方程只有一个解,为 x = ;
(2)当2 a -12=0,3 b -2=0,即 a =6, b = 时,方程有无数个解;
(3)当2 a -12=0,3 b -2≠0,即 a =6, b ≠ 时,方程无解.
解:∵方程的根始终为1,故将x=1代入方程得:
解得:4k+2a=12+1-bk,(4+b)k=13-2a,
∵k为任意实数,
∴4+b=0,13-2a=0,
∴a=6.5,b=-4.
6.
7. 小李在解方程5 a - x =13( x 为未知数)时,误将- x 看成
+ x ,得方程的解为 x =-2,则原方程的解为( C )
A. x =-3 B. x =0
C. x =2 D. x =1
C
由题意知:5 a + x =13的解为: x =-2,
将 x =-2代入5 a + x =13,5 a -2 =13 ,5 a =13+2 , a =3,所以原方程为15- x =13,解得 x =2.
8.已知a、b满足+|b-|=0,
解关于x的方程(a+2)x+b2=a﹣1.
解得:a=-4,b=
所以(-4+2)x+3=-4-1,即-2x=-8,
解得x=4.
解:根据题意得,2a+8=0,b-=0
9.已知x=-1是方程ax3+bx-3=2的解,则当x=1时,
求代数式ax3+bx-3的值.
解:将x=-1代入方程a(-1)3+b(-1)-3=2,
即a+b=-5.
当x=1时,原式=a·13+b·1-3=a+b-3=-8.
10. 已知方程6-3( x +1)=0的解与
关于 x 的方程 -3 k -2=2 x 的解互为相反数,求 k 的值.
【解】由6-3( x +1)=0,得 x =1.因为方程6-3( x +1)=0的解
与关于 x 的方程 -3 k -2=2 x 的解互为相反数,所以 x =-1是关于 x 的方程 -3 k -2=2 x 的解.将 x =-1代入,
得 -3 k -2=-2.所以 k =- .
11. 如果方程 -8=- 的解
与关于 x 的方程2 ax -(3 a +5)=5 x +12 a +20的解相同,求 a 的值.
解 : -8=- ,2( x -4)-48=-3( x +2).
5 x =50. x =10.把 x =10代入方程2 ax -(3 a +5)=5 x
+12 a +20,得2 a ×10-(3 a +5)=5×10+12 a +20,去
括号、移项,得20 a -3 a -12 a =5+50+20.合并同类
项,得5 a =75,系数化为1,得 a =15.
12.聪聪在对方程 去分母时,错误地得到了方程
,因而求得方程的解是,
试求 的值,并求方程的正确解.
解:把代入 ,得
,解得 .
所以原方程为 .
. .
. 解得 .
故方程的正确解为 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版七年级上册
第五章 一元一次方程章末复习
-------字母系数:待确定的数
1. 已知x=3是关于x的方程ax+2x-3=0的解,
求a的值
a
字母系数
待确定的数
3a+2-3=0
3a+6-3=0
3a+3=0
3a=-3
a=-1
2.方程2 x + a -4=0的解是 x =-2,求 a 的值
2+a-4=0
+a-4=0
a=4+4
a=8
a
待确定的数
常数项
3.如果方程和方程
的解相同, 的值
4. 已知关于 x 的方程9 x -3= kx +14有整数解,
求满足条件的整数 k .
解:原方程得 x = ,
当9- k =-1时, k =10;
当9- k =1时, k =8;
当9- k =17时, k =-8;
当9- k =-17时, k =26.
综上,满足条件的整数 k =10或8或-8或26.
17=1
5. 解关于 x 的方程:2 ax +2=12 x +3 b .
【解】把方程2 ax +2=12 x +3 b 变形,
得(2 a -12) x =3 b -2.
分三种情况:
(1)当2 a -12≠0,即 a ≠6时,方程只有一个解,为 x = ;
(2)当2 a -12=0,3 b -2=0,即 a =6, b = 时,方程有无数个解;
(3)当2 a -12=0,3 b -2≠0,即 a =6, b ≠ 时,方程无解.
解:∵方程的根始终为1,故将x=1代入方程得:
解得:4k+2a=12+1-bk,(4+b)k=13-2a,
∵k为任意实数,
∴4+b=0,13-2a=0,
∴a=6.5,b=-4.
6.
7. 小李在解方程5 a - x =13( x 为未知数)时,误将- x 看成
+ x ,得方程的解为 x =-2,则原方程的解为( C )
A. x =-3 B. x =0
C. x =2 D. x =1
C
由题意知:5 a + x =13的解为: x =-2,
将 x =-2代入5 a + x =13,5 a -2 =13 ,5 a =13+2 , a =3,所以原方程为15- x =13,解得 x =2.
8.已知a、b满足+|b-|=0,
解关于x的方程(a+2)x+b2=a﹣1.
解得:a=-4,b=
所以(-4+2)x+3=-4-1,即-2x=-8,
解得x=4.
解:根据题意得,2a+8=0,b-=0
9.已知x=-1是方程ax3+bx-3=2的解,则当x=1时,
求代数式ax3+bx-3的值.
解:将x=-1代入方程a(-1)3+b(-1)-3=2,
即a+b=-5.
当x=1时,原式=a·13+b·1-3=a+b-3=-8.
10. 已知方程6-3( x +1)=0的解与
关于 x 的方程 -3 k -2=2 x 的解互为相反数,求 k 的值.
【解】由6-3( x +1)=0,得 x =1.因为方程6-3( x +1)=0的解
与关于 x 的方程 -3 k -2=2 x 的解互为相反数,所以 x =-1是关于 x 的方程 -3 k -2=2 x 的解.将 x =-1代入,
得 -3 k -2=-2.所以 k =- .
11. 如果方程 -8=- 的解
与关于 x 的方程2 ax -(3 a +5)=5 x +12 a +20的解相同,求 a 的值.
解 : -8=- ,2( x -4)-48=-3( x +2).
5 x =50. x =10.把 x =10代入方程2 ax -(3 a +5)=5 x
+12 a +20,得2 a ×10-(3 a +5)=5×10+12 a +20,去
括号、移项,得20 a -3 a -12 a =5+50+20.合并同类
项,得5 a =75,系数化为1,得 a =15.
12.聪聪在对方程 去分母时,错误地得到了方程
,因而求得方程的解是,
试求 的值,并求方程的正确解.
解:把代入 ,得
,解得 .
所以原方程为 .
. .
. 解得 .
故方程的正确解为 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
