2.6探索勾股定理（2）

课件20张PPT。2.6探索勾股定理（2）1.勾股定理的内容是什么？
2.它反映的是三角形中的那些基本量之间的关系？
3.我们是用什么方法得到这个结论的？古埃及人曾用下面的方法得到直角：如图所示，他们用13个等距的结把一根绳子分成等长的12段，一个工匠同时握住绳子的第一个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角在第4个结处。引入探索如果三角形两边的平方和等于第三边平方, 那么这个三角形一定是直角三角形吗?.合作学习(1)画一个三角形,使其边长分别为3cm,4cm,5cm; 　　　　　　　　　　　　　5cm,12cm,13cm; 8cm,15cm,17cm.
(2)算一算：较短两条边的平方和与最长一条边的平方是否相等．
（３）由此你得到怎样的猜想？如果三角形两边的平方和等于第三边平方,
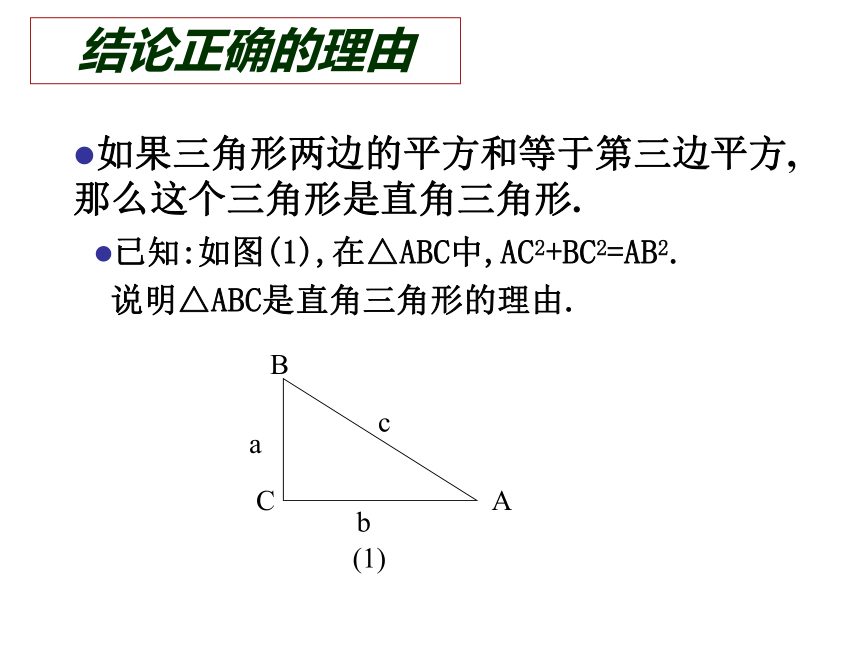
那么这个三角形是直角三角形.这是判定直角三角形的根据之一结论正确的理由如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.已知:如图(1),在△ABC中,AC2+BC2=AB2.
说明△ABC是直角三角形的理由.解:作Rt △A’B′C′使∠C′ =900,A’C′=AC,B’C′=BC(如图),则已知:如图(1),在△ABC中,AC2+BC2=AB2.
说明△ABC是直角三角形的理由.A’C′2+B’C′2=A’B′2(勾股定理).∵AC2+BC2=AB2(已知), A’C′=AC,B′C′=BC(作图),∴ AB2=A’B′2(等式性质).∴ AB=A’B′(等式性质).∴ △ABC≌ △A’B′C′(SSS).∴ ∠A=∠A′＝ 900(全等三角形的对应角相等).∴ △ABC是直角三角形(直角三角形定义).例题讲解例１．根据下列条件，分别判断以a,b,c为边的三角形是不是直角三角形．
　 (1)a=7, b=24, c=25.
(2)a=2, b=1, c=2.想一想：上述结论中，如果已判断一个三角形是直角三角形，那么哪条边所对的角是直角？满足　　　　.的三个正整数，称为勾股数。下列几组数是勾股数吗？
（1） 2， 3， 5；
（2）0.3，0.4，0.5；
（3）50，120，130；
（4）3 4 5
随堂练习随堂练习下列几组数能否作为直角三角形的三边长？说说你的理由。
（1）9，12，15；
（2）15，36，39；
（3）12，35，36；
（4）12，18，22；例２：已知△ABC的三边长分别为a,b,c.且
a=m2-n2，b=2mn,　c=m2+n2.（m，n是正整数，且m＞n）． △ABC是直角三角形吗？请说明理由．例题讲解例３.一个零件的形状如图1所示，按规定这个零件中∠A和 ∠ DBC都应为直角。工人师傅量得这个零件个边尺寸如图2所示，这个零件符合要求吗？图1图23451213 例题讲解(1).AC的长是多少？
(2).△ABC， △ACD是直角三角形吗？为什么？
(3).这个四边形的面积是多少？
思考题２．已知:如图, △ABC中，CD是AB边上的　　　　高，且CD2=AD.BD
说明 △ABC是直角三角形的理由。解后反思：
本节课的结论，是另一种判定直角三角形的方法，它仅仅依据三边的长度之间的数量关系，就可以作出判断，而不必计算角的大小。思考题1. 如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是 ( )
是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.BA练习三角形的三边分别是a,b,c, 且满足等式(a+b)2-c2=2ab, 则此三角形是: ( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.已知?ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.5. 以?ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.A直角直角∠ A四边形ABCD中已知AB=3, BC=4, CD=12, DA=13, 且∠ABC=900,求这个四边形的面积.7、请你写出三组勾股数；
8、一组勾股数的倍数一定是勾股数吗？为什么?
补充思考题：
△ABC中，AB=17cm, BC=30cm, BC上中线AD=8cm，请你判断△ABC
的形状，并说明理由。归纳小结勾股定理
直角三角形两直角边的平方和等于斜边的平方．如果三角形两边的平方和等于第三边平方,
那么这个三角形是直角三角形.作业（1）书本作业题
（2）作业本．
　 再 见