四边形复习

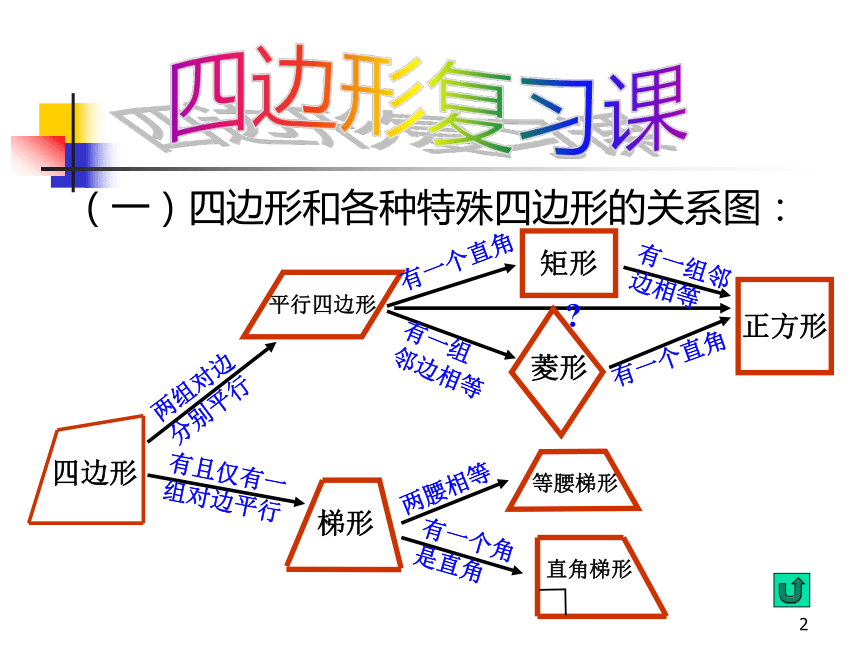
课件32张PPT。1四边形复习课2四边形复习课（一）四边形和各种特殊四边形的关系图：四边形两组对边
分别平行平行四边形有一个直角矩形有一组
邻边相等菱形有一组邻
边相等有一个直角正方形有且仅有一
组对边平行梯形两腰相等有一个角
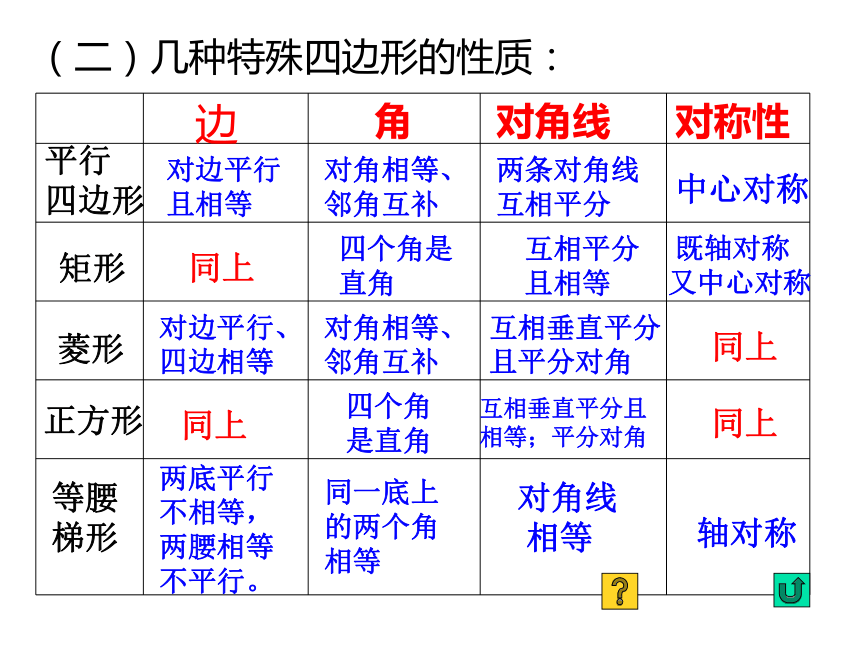
是直角等腰梯形直角梯形??（二）几种特殊四边形的性质：平行
四边形边角对角线对称性对边平行
且相等对角相等、
邻角互补两条对角线
互相平分中心对称矩形同上四个角是
直角互相平分
且相等 既轴对称
又中心对称菱形对边平行、
四边相等对角相等、
邻角互补互相垂直平分
且平分对角同上正方形同上四个角
是直角互相垂直平分且
相等；平分对角同上等腰
梯形两底平行
不相等，
两腰相等
不平行。同一底上
的两个角
相等对角线
相等轴对称（三）几种特殊四边形的常用判定方法：平行
四边形(1) 两组对边分别平行;矩形(2)是平行四边形，且有一个角是直角；菱形 （2）是平行四边形，且有一组邻边
相等；（1）是矩形，并且有一组邻边相等；
（2）是菱形，并且有一个角是直角；正方形等腰
梯形 （1）是梯形，并且同一底上的两个角相等；
（2）是梯形，并且两条对角线相等。(2) 两组对边分别相等；(3) 一组对边平行且相等；(4) 两条对角线互相平分；(5) 两组对角分别相等；(1) 有三个直角；（3） 是平行四边形，并且两条对角线相等；（1）四条边都相等;（3）是平行四边形，并且两条对角线互相垂直；（四）其它重要定理： 图形 内角和 外角和
三角形：
四边形：
n边形： （2）两条平行线之间的垂线段处处相等（P87 )

（3）直角三角形斜边上的中线等于斜边的一半。

（P98） （1）内角和、外角和定理： 180° 360°
360° 360 °
（n-2）180° 360° 6四边形复习课（五）特殊四边形的面积：
（1） S平行四边形 = 底?高
（2） S矩形 = 长?宽
（3） S菱形 = 底?高
（4） S正方形 = 边长2
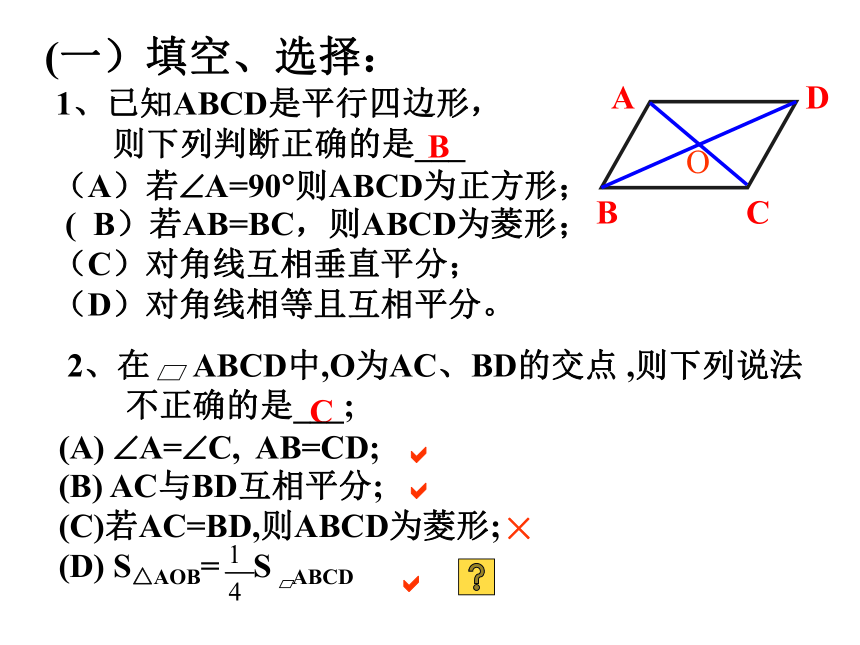
（5） S梯形 =（上底+下底）?高?2= 对角线之积的一半1、已知ABCD是平行四边形，
则下列判断正确的是___
（A）若?A=90?则ABCD为正方形； ( ( B）若AB=BC，则ABCD为菱形；
（C）对角线互相垂直平分；
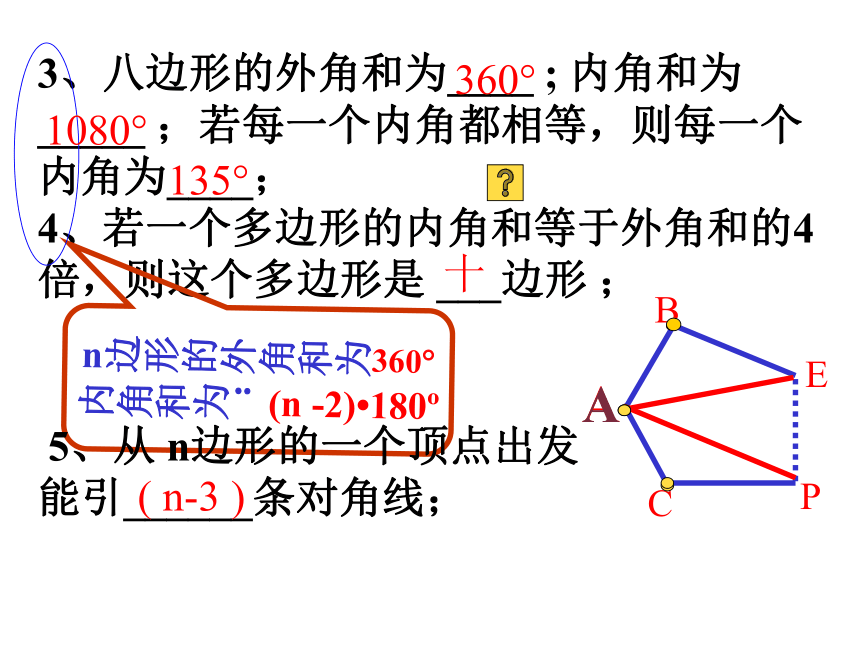
（D）对角线相等且互相平分。 BC(一）填空、选择：???×3、八边形的外角和为____ ; 内角和为_____ ；若每一个内角都相等，则每一个内角为____；
4、若一个多边形的内角和等于外角和的4倍，则这个多边形是 ___边形 ；
n边形的外角和为360?
内角和为：(n -2)?180o
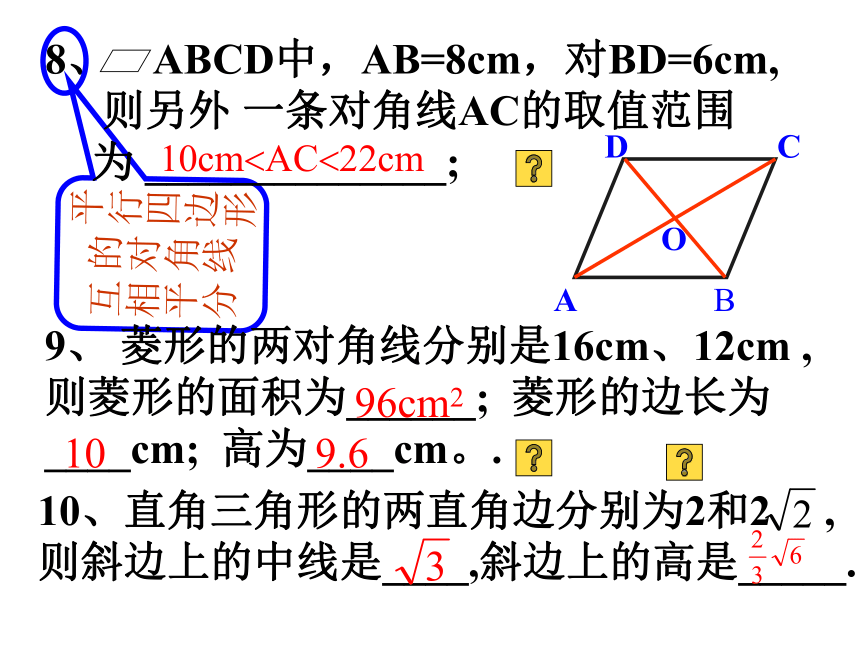
5、从 n边形的一个顶点出发能引______条对角线；1080?360?135?十( n-3 )A 6、一个五边形五条边之比为1:2:3:4:5，且最长边为10米，则它的周长是_____ ; 30cm7、平行四边形的对角线______; 菱形的对角线_________; 矩形的对角线_______; 正方形的对角线____________;等腰梯形的对角线____.
(A) 互相垂直; (B) 互相平分;
(C) 相等; (D)平分对角.BA、B、DB、CA、B、C、DC平行四边形
的对角线
互相平分9、 菱形的两对角线分别是16cm、12cm , 则菱形的面积为______; 菱形的边长为____cm; 高为____cm。.10cm?AC?22cm96cm2109.610、直角三角形的两直角边分别为2和2 ,
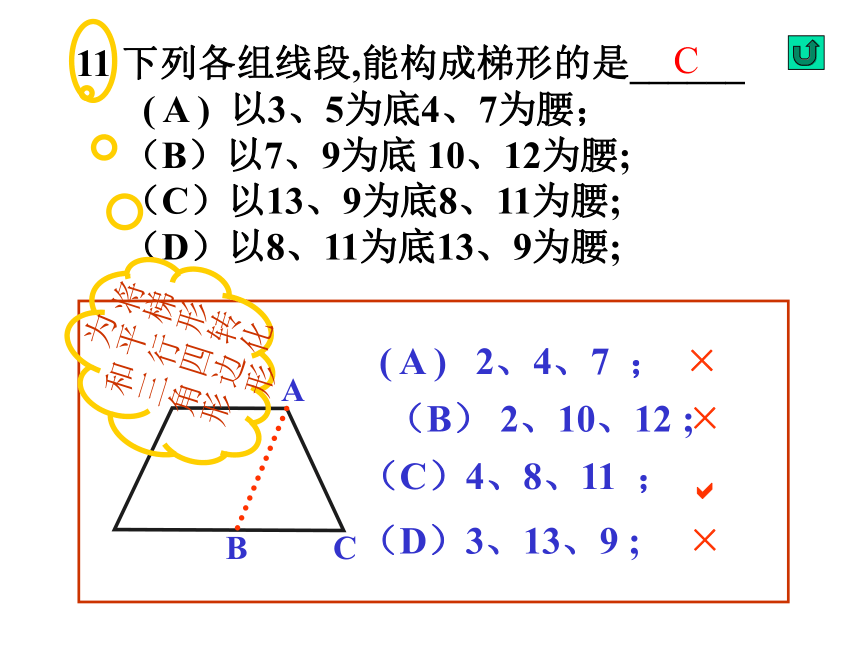
则斜边上的中线是____,斜边上的高是_____. 11 下列各组线段,能构成梯形的是______
( A ) 以3、5为底4、7为腰；
（B）以7、9为底 10、12为腰;
（C）以13、9为底8、11为腰;
（D）以8、11为底13、9为腰; ( A ) 2、4、7 ；（B） 2、10、12 ; ××（C）4、8、11 ；?（D）3、13、9 ;×将梯形转化
为平行四边形
和三角形C 11、 下列各组线段,能构成梯形的是______
( A ) 以3、5为底4、7为腰；
（B）以7、9为底 10、12为腰;
（C）以13、9为底8、11为腰;
（D）以8、11为底13、9为腰; ( A ) 2、4、7 ；（B） 2、10、12 ; ××（C）4、8、11 ；?（D）3、13、9 ;×C (1) 本节课复习了本章的所有知识点 ,课后要巩固;
(2) 特殊四边形的对角线性质在解题时运用较多,
例如:
① 矩形的对角线构成两组全等的等腰三角形;
②菱形的对角线构成四个全等的直角三角形;
③正方形的对角线构成四个全等的等腰直角
三角形.
(3) 直角三角形斜边上的中线定理在计算题、
证明题中应用都非常广泛,要熟练应用。四、课堂小结:14五、课后作业：
四边形复习课15四边形复习课再见！多谢合作！
请多指教！ ∵S △AOB= S△BOC

= S△ABC ?△ABC≌△CDA（等底同高） ∵S △AOB= S△BOC

= S△ABC ?△ABC≌△CDA（等底同高） (3) 八边形的内角和为：
(8 -2)?180o=1080o(4) 内角和=外角和×4
（n-2）·180o=360o ×4
?n=10其中每一个内角为：
1080o÷8=135o (3) 八边形的内角和为：
(8 -2)?180o=1080o(4) 内角和=外角和×4
（n-2）·180o=360o ×4
?n=10其中每一个内角为：
1080o÷8=135o（6）设比例的一份为xcm，则:5x = 10
? x = 2
∴ 周长为 ：（1+2+3+4+5）x
= 15×2
= 30（cm） （6）设比例的一份为xcm，则:5x = 10
? x = 2
∴ 周长为 ：（1+2+3+4+5）x
= 15×2
= 30（cm） 在?AOB中
OB=3 AB=8
则 8 - 3 < OA < 8 + 3
即 5 < OA < 11
? 10 < AC < 22 在?AOB中
OB=3 AB=8
则 8 - 3 < OA < 8 + 3
即 5 < OA < 11
? 10 < AC < 22 （1） 在Rt?ABC中，
? AB= =
? CD = AB =?（2） （1） 在Rt?ABC中，
? AB= =
? CD = AB =?（2） ∵ 菱形的对角线互相垂直
∴ 在Rt?AOB中， (9) S菱形= ?AC?BD = 96（cm2）AB = = 10 ；高 h = = 9.6 ∵ 菱形的对角线互相垂直
∴ 在Rt?AOB中， (9) S菱形= ?AC?BD = 96（cm2）AB = = 10 ；高 h = = 9.628九、几种常见的平行四边形辅助线的画法：1.对角线2.构建新的平行四边形293.构建全等三角形4.构建等腰三角形30十常见的梯形的辅助线画法：1.构建平行四边形2.平移一条对角线EE313.构建全等三角形F4.构建矩形325.作梯形的中位线6.构建大平行四边形7.构建三角形EO