第五章 一元一次方程章末复习----易错题 课件(共19张PPT)
文档属性
| 名称 | 第五章 一元一次方程章末复习----易错题 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 21:29:19 | ||
图片预览





文档简介
(共19张PPT)
第五章 一元一次方程章末复习
---易错题
浙教版七年级上册
1. (1) +(-x + 3)
(2) 2(x + 8)
= 2x + 16
= 120t - 60
= - x + 3
2. (1) -3(3x + 4)
= -9x - 12
= -120t + 60
一、去括号
= x + 3
(3) 120(t - 0.5)
(2) -120(t - 0.5)
(3) -(-x - 3)
与数的运算一样,进行整式的运算时也会遇到去括号的问题。
一般地,一个数与一个多项式相乘,需要去括号,去括号就是用括号外的数乘括号内的每一项,再把所得的积相加。
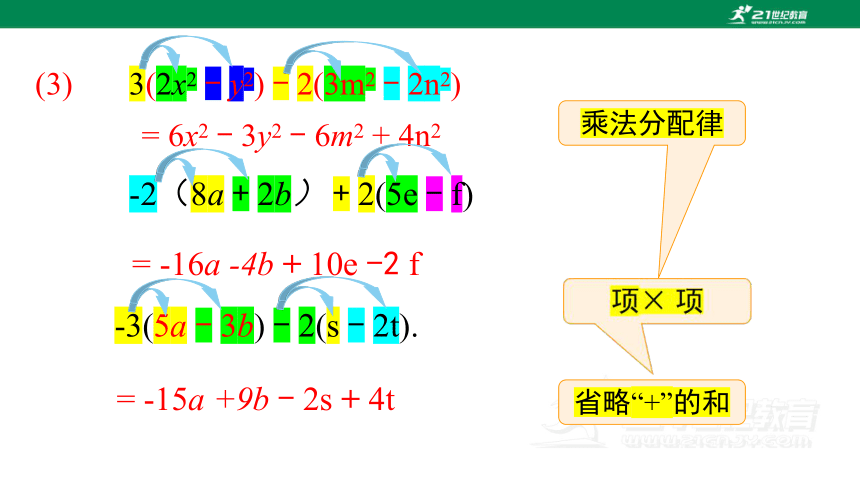
(3) 3(2x2 - y2) - 2(3m2 - 2n2)
= 6x2 - 3y2 - 6m2 + 4n2
-2(8a + 2b) + 2(5e - f)
= -16a -4b + 10e -2 f
= -15a +9b - 2s + 4t
-3(5a - 3b) - 2(s - 2t).
乘法分配律
项
省略“+”的和
二、添括号
(1) a - b - c + d = a - ( );
b + c - d
1. 所添括号前面是“+”号,括到括号里的各项都不改变正负号.
2. 所添括号前面是“-”号,括到括号里的各项都改变正负号.
添括号与去括号的过程正好相反,添括号是否正确,可以用去括号法则检验!
(2) x2 - x + 1 = x2 - ( );
x - 1
3x + 1
(3) 2x2 - 6x - 2 = 2x2 - 2( );
图书馆内原有 a 位同学. 后来有些同学因上课要离开,第一批走了 b 位同学,第二批又走了 c 位同学.
试用两种方式写出图书馆内还剩下的同学数,
你能从中发现什么关系?
a - (b + c)
a - b - c
=
a - b - c
a - (b + c)
=
三;下面方程的解法对吗?若不对,请改正。
解:去分母,得 2(3x-1)=1-4x-1
去括号,得 6x-1=1-4x-1
移项,得 6x-4x=1-1+1
∴2x=1 即x=0.5
解方程
2(3x-1)=16-(4x-1)
6x-2=6-4x+1
6x+4x=6+1+2
∴10x=9 即 x=0.9
一步错,错!错!错!
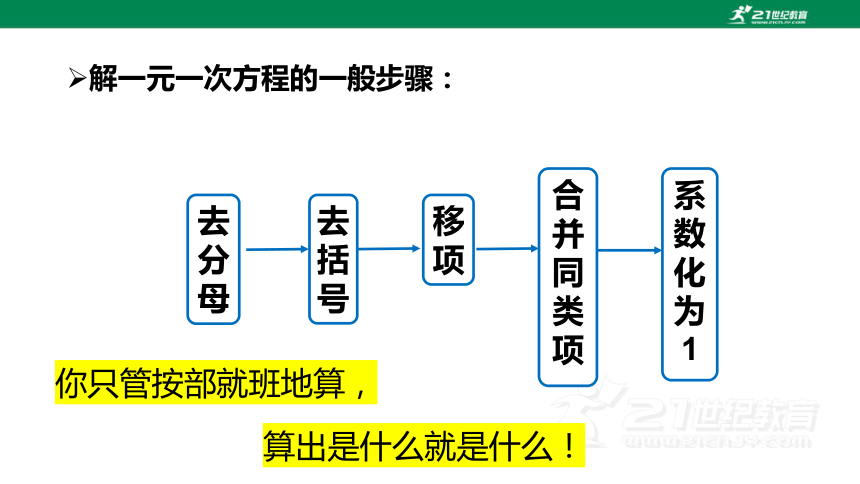
解一元一次方程的一般步骤:
移项
合并同类项
系数化为
1
去括号
去分母
你只管按部就班地算,
算出是什么就是什么!
5(3x+1)– 10×2 =(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
去分母
去括号
依据:等式的性质2.
依据:分配律.
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
移项
系数化为1
依据:等式的性质1.
依据:等式的性质2.
依据:分配律
合并同类项
5.为了加强公民的节水意识,合理利用水资源,
某市采用阶梯价格调控手段达到节水目的,其价目表如下.
每月用水量 价格
不超出 的部分 2元/
超过,不超过 的部分 4元/
超出 的部分 8元/
(1)某户居民1月份用水 ,试求1月份的水费为多少元?
解: (元).
答:1月份的水费为11元.
(2)若某户居民5月份共交水费22元,
则该户居民5月份实际用水多少立方米?
解:(元), (元),
每月用水量 价格
不超出 的部分 2元/
超过,不超过 的部分 4元/
超出 的部分 8元/
且 ,∴该户居民5月份实际用水量超过但不超过 .
设该户居民5月份实际用水 , , 解得 .
答:该户居民5月份实际用水 .
6.唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.
《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,
饮尽壶中酒.试问能算士,如何知原有(注:古代一斗是10升).
大意是:李白在郊外春游时,做出这样一条约定,
遇见朋友,到酒店里先将壶里的酒增加一倍,再喝掉其中的5升酒.
按照这样的约定,在第3个店里正好喝光了壶中的酒.请问各位,
壶中原有多少升酒?
解:设壶中原有 升酒.根据题意,得 , .
答:壶中原有 升酒.
8
(1) 46x=460+x,
x64=100x+64;
(2) 12(460+x)=21(100x+64);
(3) x=2;
(4) ∵462×12=5544
264 ×21=5544
∴462×12=264×21
8.定义一种新运算“※”: a ※ b = a -2 b .
例如:2※(-3)=2-2×(-3)=2+6=8.
(1)求(-3)※2的值;
【解】原式=-3-2×2=-3-4=-7.
(2)若( x -3)※( x +1)=1,求 x 的值.
解 : ( x-3 )-2( x +1)=1, x -3-2 x -2=1,
- x =6, x =-6.
9. 先阅读下列解题过程,再解答问题.
解方程:| x +5|=3.
解:当 x +5≥0时, x +5=3,x =-2;
当 x +5<0时, x +5=-3,x =-8.
所以原方程的解是 x =-2或 x =-8.
按上面的解法解方程:|3 x -1|-5=0.
【解】|3 x -1|=5.
当3 x -1≥0时,3 x -1=5, x =2.
当3 x -1<0时,3 x -1=-5, x =- .
综上: x1 =2或 x 2=- .
10. 若关于 x 的方程 (m - 4)x|m|-3 = 0 是一元一次方程,
则 m 的值是( )
A. 4 B. -4 C. ±4 D. 5
一元一次方程的概念
|m|-3 = 1
m-4 ≠ 0
m = ±4
m ≠ 4
m = -4
B
11.某中学七年级三个班的同学分别向希望小学捐赠图书,已知三个班
级学生捐赠图书册数之比为 .如果他们共捐了198册,那么这三个
班级各捐多少册?
解:设三个班分别捐了册,册, 册.由题意,得
,
解得 .
,, .
答:三个班分别捐了55册,66册,77册.
6. 某次知识竞赛共20道题,每答对一题得8分,答错或不答要扣3分. 某选手在这次竞赛中共得 116 分,那么他答对几道题?
解:设答对了 x 道题,
由题意得:8x-(20-x)×3=116.
解得 x=16.
答:他答对16道题.
则有 (20-x) 道题答错或不答,
方程是现实问题中含有未知数的相等关系的数学表达
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第五章 一元一次方程章末复习
---易错题
浙教版七年级上册
1. (1) +(-x + 3)
(2) 2(x + 8)
= 2x + 16
= 120t - 60
= - x + 3
2. (1) -3(3x + 4)
= -9x - 12
= -120t + 60
一、去括号
= x + 3
(3) 120(t - 0.5)
(2) -120(t - 0.5)
(3) -(-x - 3)
与数的运算一样,进行整式的运算时也会遇到去括号的问题。
一般地,一个数与一个多项式相乘,需要去括号,去括号就是用括号外的数乘括号内的每一项,再把所得的积相加。
(3) 3(2x2 - y2) - 2(3m2 - 2n2)
= 6x2 - 3y2 - 6m2 + 4n2
-2(8a + 2b) + 2(5e - f)
= -16a -4b + 10e -2 f
= -15a +9b - 2s + 4t
-3(5a - 3b) - 2(s - 2t).
乘法分配律
项
省略“+”的和
二、添括号
(1) a - b - c + d = a - ( );
b + c - d
1. 所添括号前面是“+”号,括到括号里的各项都不改变正负号.
2. 所添括号前面是“-”号,括到括号里的各项都改变正负号.
添括号与去括号的过程正好相反,添括号是否正确,可以用去括号法则检验!
(2) x2 - x + 1 = x2 - ( );
x - 1
3x + 1
(3) 2x2 - 6x - 2 = 2x2 - 2( );
图书馆内原有 a 位同学. 后来有些同学因上课要离开,第一批走了 b 位同学,第二批又走了 c 位同学.
试用两种方式写出图书馆内还剩下的同学数,
你能从中发现什么关系?
a - (b + c)
a - b - c
=
a - b - c
a - (b + c)
=
三;下面方程的解法对吗?若不对,请改正。
解:去分母,得 2(3x-1)=1-4x-1
去括号,得 6x-1=1-4x-1
移项,得 6x-4x=1-1+1
∴2x=1 即x=0.5
解方程
2(3x-1)=16-(4x-1)
6x-2=6-4x+1
6x+4x=6+1+2
∴10x=9 即 x=0.9
一步错,错!错!错!
解一元一次方程的一般步骤:
移项
合并同类项
系数化为
1
去括号
去分母
你只管按部就班地算,
算出是什么就是什么!
5(3x+1)– 10×2 =(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
去分母
去括号
依据:等式的性质2.
依据:分配律.
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
移项
系数化为1
依据:等式的性质1.
依据:等式的性质2.
依据:分配律
合并同类项
5.为了加强公民的节水意识,合理利用水资源,
某市采用阶梯价格调控手段达到节水目的,其价目表如下.
每月用水量 价格
不超出 的部分 2元/
超过,不超过 的部分 4元/
超出 的部分 8元/
(1)某户居民1月份用水 ,试求1月份的水费为多少元?
解: (元).
答:1月份的水费为11元.
(2)若某户居民5月份共交水费22元,
则该户居民5月份实际用水多少立方米?
解:(元), (元),
每月用水量 价格
不超出 的部分 2元/
超过,不超过 的部分 4元/
超出 的部分 8元/
且 ,∴该户居民5月份实际用水量超过但不超过 .
设该户居民5月份实际用水 , , 解得 .
答:该户居民5月份实际用水 .
6.唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.
《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,
饮尽壶中酒.试问能算士,如何知原有(注:古代一斗是10升).
大意是:李白在郊外春游时,做出这样一条约定,
遇见朋友,到酒店里先将壶里的酒增加一倍,再喝掉其中的5升酒.
按照这样的约定,在第3个店里正好喝光了壶中的酒.请问各位,
壶中原有多少升酒?
解:设壶中原有 升酒.根据题意,得 , .
答:壶中原有 升酒.
8
(1) 46x=460+x,
x64=100x+64;
(2) 12(460+x)=21(100x+64);
(3) x=2;
(4) ∵462×12=5544
264 ×21=5544
∴462×12=264×21
8.定义一种新运算“※”: a ※ b = a -2 b .
例如:2※(-3)=2-2×(-3)=2+6=8.
(1)求(-3)※2的值;
【解】原式=-3-2×2=-3-4=-7.
(2)若( x -3)※( x +1)=1,求 x 的值.
解 : ( x-3 )-2( x +1)=1, x -3-2 x -2=1,
- x =6, x =-6.
9. 先阅读下列解题过程,再解答问题.
解方程:| x +5|=3.
解:当 x +5≥0时, x +5=3,x =-2;
当 x +5<0时, x +5=-3,x =-8.
所以原方程的解是 x =-2或 x =-8.
按上面的解法解方程:|3 x -1|-5=0.
【解】|3 x -1|=5.
当3 x -1≥0时,3 x -1=5, x =2.
当3 x -1<0时,3 x -1=-5, x =- .
综上: x1 =2或 x 2=- .
10. 若关于 x 的方程 (m - 4)x|m|-3 = 0 是一元一次方程,
则 m 的值是( )
A. 4 B. -4 C. ±4 D. 5
一元一次方程的概念
|m|-3 = 1
m-4 ≠ 0
m = ±4
m ≠ 4
m = -4
B
11.某中学七年级三个班的同学分别向希望小学捐赠图书,已知三个班
级学生捐赠图书册数之比为 .如果他们共捐了198册,那么这三个
班级各捐多少册?
解:设三个班分别捐了册,册, 册.由题意,得
,
解得 .
,, .
答:三个班分别捐了55册,66册,77册.
6. 某次知识竞赛共20道题,每答对一题得8分,答错或不答要扣3分. 某选手在这次竞赛中共得 116 分,那么他答对几道题?
解:设答对了 x 道题,
由题意得:8x-(20-x)×3=116.
解得 x=16.
答:他答对16道题.
则有 (20-x) 道题答错或不答,
方程是现实问题中含有未知数的相等关系的数学表达
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
