6.2菱形(2)

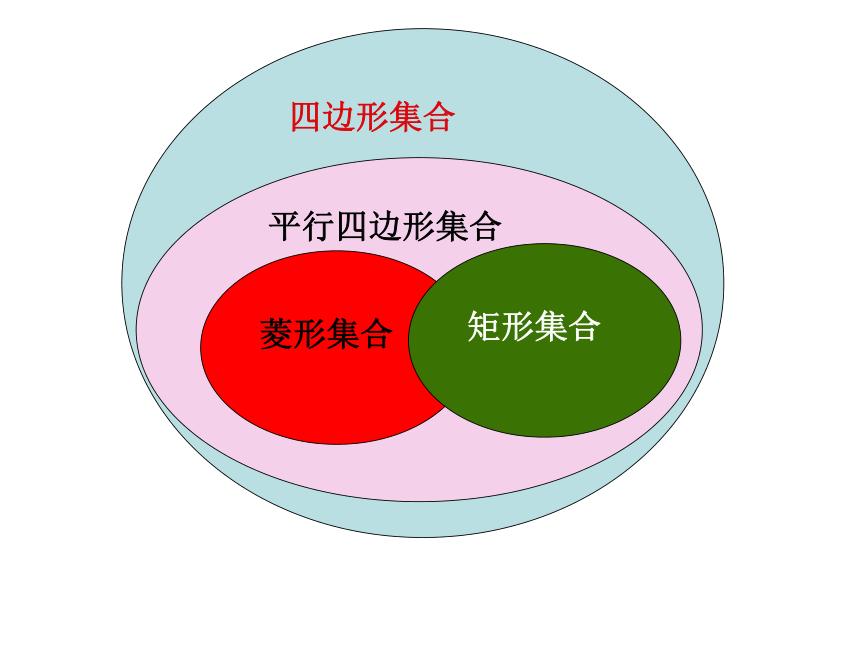
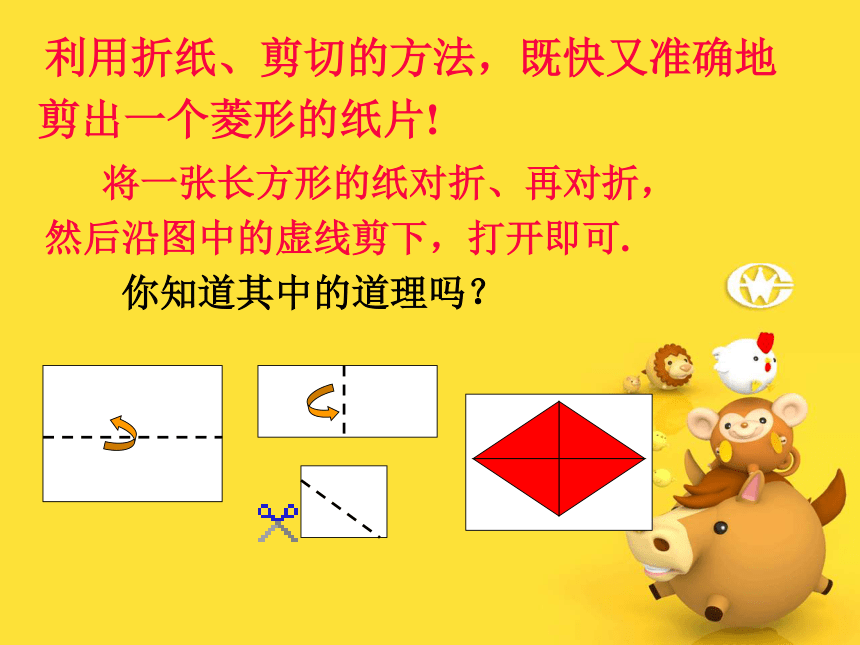
课件24张PPT。6.2菱形 (2)平行四边形菱形一组邻边相等菱形的定义有一组邻边相等的平行四边形叫做菱形对边平行且相等四条边都相等中心对称图形轴对称图形对角相等邻角互补对角线互相垂直对角线互相平分每一条对角线平分一组对角用列表形式小结出菱形的性质1、底乘以高2、 （a，b表示两条对角线的长度） 将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可.
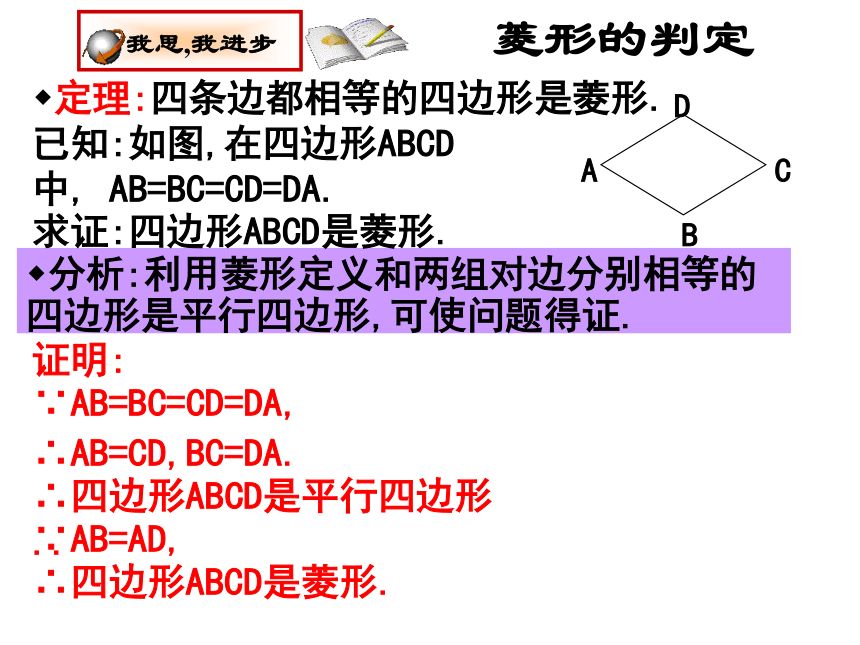
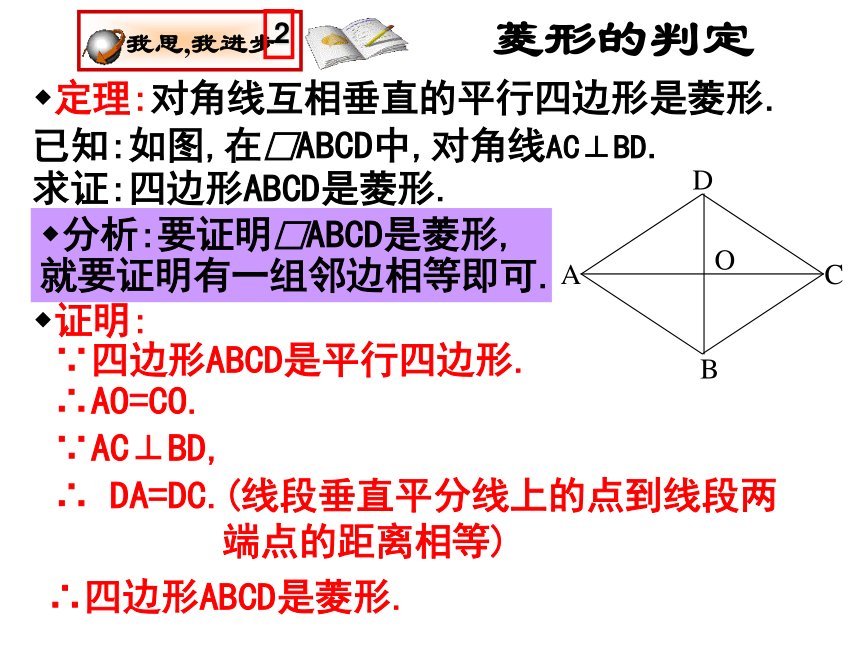
你知道其中的道理吗？ 利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片!菱形的判定定理:四条边都相等的四边形是菱形. 我思,我进步已知:如图,在四边形ABCD中, AB=BC=CD=DA.分析:利用菱形定义和两组对边分别相等的四边形是平行四边形,可使问题得证.证明:∵AB=BC=CD=DA,∴AB=CD,BC=DA.∴四边形ABCD是平行四边形..求证:四边形ABCD是菱形.∵AB=AD,∴四边形ABCD是菱形.菱形的判定定理:对角线互相垂直的平行四边形是菱形.已知:如图,在□ABCD中,对角线AC⊥BD.求证:四边形ABCD是菱形.分析:要证明□ABCD是菱形,就要证明有一组邻边相等即可.证明:∴AO=CO.∵AC⊥BD,∴ DA=DC.∵四边形ABCD是平行四边形.∴四边形ABCD是菱形.(线段垂直平分线上的点到线段两端点的距离相等)1.一组邻边相等的平行四边形是菱形.
2.四条边都相等的四边形是菱形.
3.对角线互相垂直的平行四边形是菱形.

“对角线互相垂直平分的四边形是菱形”是真命题还是假命题?为什么? 想一想怎样判别一个四边形(平行四边形)是菱形?判断下列说法是否正确？为什么？
(1)对角线互相垂直的四边形是菱形；
(2)对角线互相垂直平分的四边形是菱形；
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形；
(4)两条邻边相等，且一条对角线平分一
组对角的四边形是菱形． □ABCD的对角线AC与BD相交于点O，
（1）若AB=AD，则□ABCD是 形； （2）若AC=BD，则□ABCD是 形； （3）若∠ABC是直角，则□ABCD是 形； （4）若∠BAO=∠DAO，则□ABCD是 形。矩菱矩菱 学以致用已知，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F。求证：四边形AEDF是菱形。 证明:∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形∵DE∥AC,∴平行四边形AEDF是菱形.∴∠ADE=∠DAF.∵AD是△ABC的角平分线,∴∠DAE=∠DAF.∴AE=ED.∴∠DAE=∠ADE.已知：如图,□ ABCD的对角线AC的垂直平分线与边AD，BC分别交于E，F．
求证：四边形AFCE是菱形如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，求证：四边形EFGH是菱形。如图,在△ABC中,∠BAC=90°,AD⊥BC于D,
CE平分∠ACB,交AD于G,交AB于E,EF⊥BC
于F,四边形AEFG是菱形吗?如图:将菱形ABCD沿AC方向平移至A1B1C1D1,
A1D1交CD于E,A1B1交BC于F,请问四边形
A1FCE是不是菱形?为什么?∟∟EF把两张等宽的纸条交叉重叠在一起，你能判断重叠部分ABCD的形状吗？请你动脑筋菱形的判定定理:四条边都相等的四边形是菱形.定理:对角线互相垂直的平行四边形是菱形.在四边形ABCD中,
∵AB=BC=CD=AD,∴四边形ABCD是菱形.∵AC,BD是□ABCD的两条对角线,AC⊥BD.∴四边形ABCD是菱形.学以致用 1、如图，在一种可伸缩的衣帽架中，每个菱形的周长都为100厘米，固定在墙上的两点A、B之间的距离为25厘米，则∠ACB= .ABC小试牛刀（3）在菱形ABCD中∠BAC=30°，BD=6㎝，则 ∠BAD= ,∠ABD= ,AB= . 60 °60 °6㎝小试牛刀（2）已知：菱形ABCD中，对角线AC与BD相交于点O，且 AC=12，BD=16，则菱形ABCD的面积为 ，边长为 ，周长为 。（1）在菱形ABCD中，∠BAD=2∠B，则∠B= , △ABC是 三角形，∠ABD的度数为________ 。等边30 °96104060 ° 大显身手O解:∵花坛ABCD是菱形
∴AC⊥BD, ∠ABO= ∠ABC=300
在Rt△OAB中 ,AO=AB= ×20=10(m),
BO= = ≈17.32(m).
∴花坛的两条小路长
AC=2AO=20(m),
BD=2BO ≈34.64(m).
花坛的面积
S菱形ABCD=4× S △OAB=AC×BD ≈346.40(m2).1、已知,在菱形ABCD中,∠BAD= ,现将一块含 角的三角尺AMN(其中∠NAM= )叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系?请你通过动手操作、度量、猜想、验证等方法予以探索。挑战自我2.菱形ABCD中∠ABC=60°,AB=4cm,P为BD上任意一点,E为BC中点,求PE+PC的最小值.例.如图，将一张边长为4的菱形纸片ABCD固定在一个建立了平面直角坐标系的木板上，A，B在x轴上，D在y轴的正半轴上，C在第一象限， ∠BAD=60° 。
（1）求A、B、C、D的坐标；
（2）求过B、C两点的直线的解析式。E