5.5 一元一次方程的应用(2) 课件(共17张PPT)
文档属性
| 名称 | 5.5 一元一次方程的应用(2) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
5.4 一元一次方程的应用(2)
浙教版七年级上册数学
解 设标志性建筑底面的边长为x米,
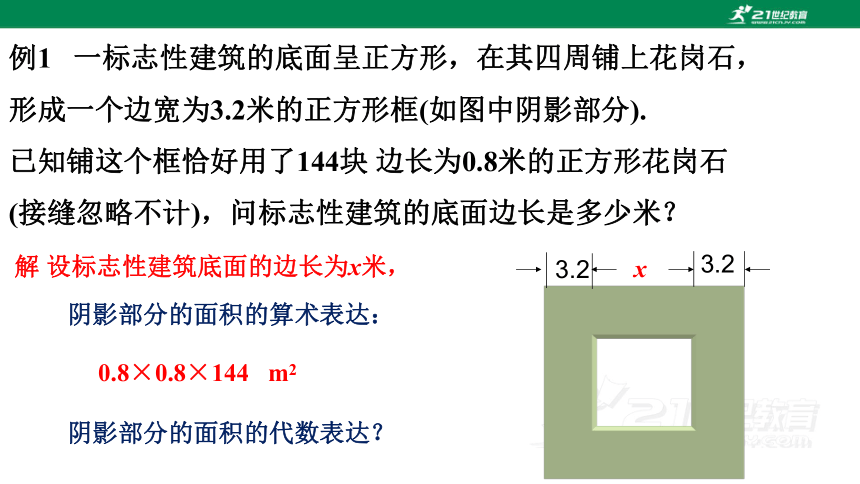
例1 一标志性建筑的底面呈正方形,在其四周铺上花岗石,
形成一个边宽为3.2米的正方形框(如图中阴影部分).
已知铺这个框恰好用了144块 边长为0.8米的正方形花岗石
(接缝忽略不计),问标志性建筑的底面边长是多少米?
阴影部分的面积的算术表达:
0.8×0.8×144 m2
3.2
3.2
x
阴影部分的面积的代数表达?
3.2
3.2
x
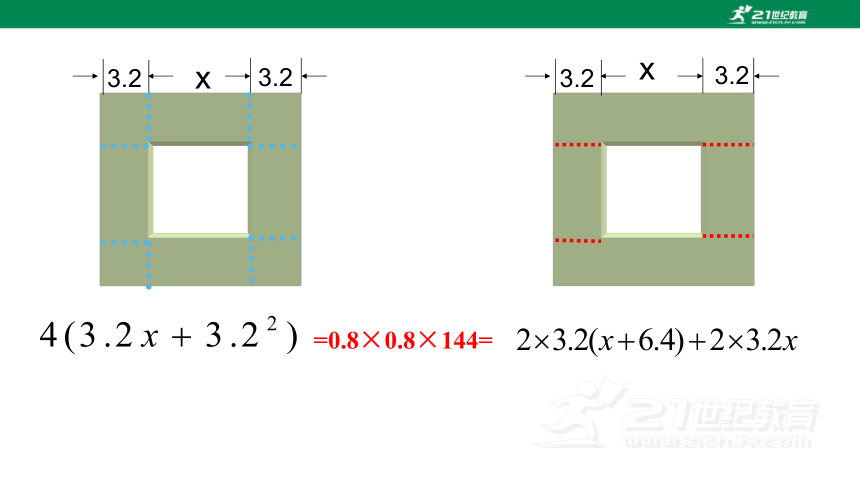
3.2
3.2
x
=0.8×0.8×144=
3.2
3.2
x
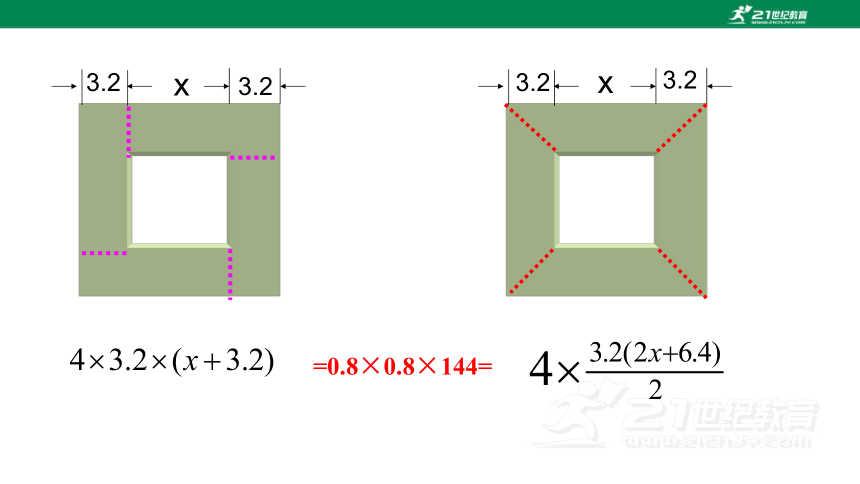
3.2
3.2
x
=0.8×0.8×144=
x=4.
4×3.2(x+3.2)=0.8×0.8×144.
阴影部分的面积的算术表达:
0.8×0.8×144 m2
阴影部分的面积的代数表达:
4×3.2(x+3.2) m2
注意
在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其是相等关系是建立方程的关键.解题中的检验对确保答案的正确和合理很有帮助,但具体过程可以省略不写.
解 设截取圆柱的高为x(mm),
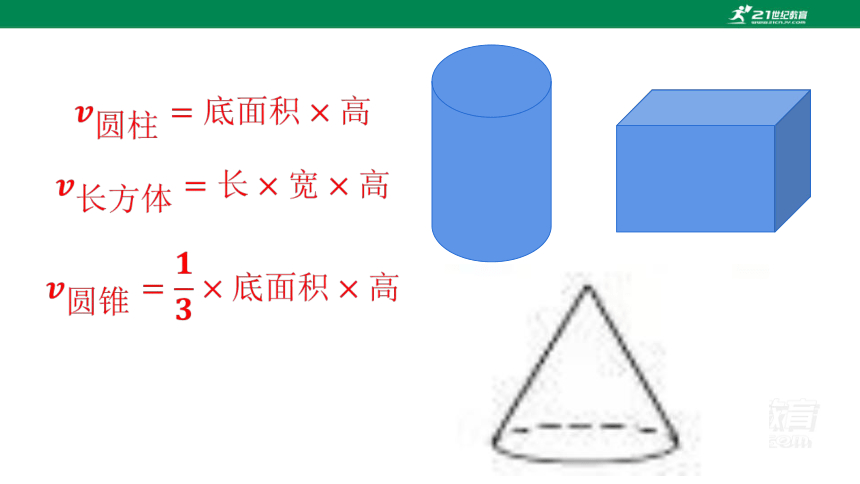
例2 如图,用直径为200 mm的钢柱锻造一块长、宽、高分别为 300 mm,300 mm和80 mm的长方体毛坯底板.问应截取钢柱多少长(不计损耗,结果误差不超过1mm)
π×1002×x=300×300×80.
长方体毛坯底板的体积的算术表达:
300×300×80 mm3.
钢柱的体积的代数表达:
π×1002×x mm3.
(1)底面积、高度发生了变化,体积和质量都保持不变
(2)围成图形的面积发生了变化,但铁丝长度保持不变
(3)形状改变,体积不变
夯实基础,稳扎稳打
解,设能放x本厚为2.1cm的书,
2.1x=6.3
x=
解,设将上底缩小 x m,
30(60-x)=
x=15
长方形面积的代数表达:
30(60-x) m2
梯形面积的算术表达:
3.
解,设需 x 千克小麦,
x 千克小麦磨成面粉的代数表达:
(1-15%)x 千克
(1-15%)x =5100
x =6000
4.
解,设B容器底面积为S cm2,
A容器底面积的代数表达:
2S cm2
水倒入B容器后,B容器水深为x cm,
A容器水的体积的代数表达:
2S
B容器水的体积的代数表达:
S
2SS
连续递推,豁然开朗
5.
解,设容器内的水将升高 x cm,
容器内的水的体积的算术表达:
容器内的水的体积的代数表达:
6.
1、在解决图形问题时,
要抓住用不同方法表示出来的图形面积相等这一关系列出方程即可.
2、在解决等积变形问题时,首先要找到在变化过程中不变量,
善于利用图形的面积、体积、周长及质量等捕捉等量关系,从而列出方程.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
5.4 一元一次方程的应用(2)
浙教版七年级上册数学
解 设标志性建筑底面的边长为x米,
例1 一标志性建筑的底面呈正方形,在其四周铺上花岗石,
形成一个边宽为3.2米的正方形框(如图中阴影部分).
已知铺这个框恰好用了144块 边长为0.8米的正方形花岗石
(接缝忽略不计),问标志性建筑的底面边长是多少米?
阴影部分的面积的算术表达:
0.8×0.8×144 m2
3.2
3.2
x
阴影部分的面积的代数表达?
3.2
3.2
x
3.2
3.2
x
=0.8×0.8×144=
3.2
3.2
x
3.2
3.2
x
=0.8×0.8×144=
x=4.
4×3.2(x+3.2)=0.8×0.8×144.
阴影部分的面积的算术表达:
0.8×0.8×144 m2
阴影部分的面积的代数表达:
4×3.2(x+3.2) m2
注意
在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其是相等关系是建立方程的关键.解题中的检验对确保答案的正确和合理很有帮助,但具体过程可以省略不写.
解 设截取圆柱的高为x(mm),
例2 如图,用直径为200 mm的钢柱锻造一块长、宽、高分别为 300 mm,300 mm和80 mm的长方体毛坯底板.问应截取钢柱多少长(不计损耗,结果误差不超过1mm)
π×1002×x=300×300×80.
长方体毛坯底板的体积的算术表达:
300×300×80 mm3.
钢柱的体积的代数表达:
π×1002×x mm3.
(1)底面积、高度发生了变化,体积和质量都保持不变
(2)围成图形的面积发生了变化,但铁丝长度保持不变
(3)形状改变,体积不变
夯实基础,稳扎稳打
解,设能放x本厚为2.1cm的书,
2.1x=6.3
x=
解,设将上底缩小 x m,
30(60-x)=
x=15
长方形面积的代数表达:
30(60-x) m2
梯形面积的算术表达:
3.
解,设需 x 千克小麦,
x 千克小麦磨成面粉的代数表达:
(1-15%)x 千克
(1-15%)x =5100
x =6000
4.
解,设B容器底面积为S cm2,
A容器底面积的代数表达:
2S cm2
水倒入B容器后,B容器水深为x cm,
A容器水的体积的代数表达:
2S
B容器水的体积的代数表达:
S
2SS
连续递推,豁然开朗
5.
解,设容器内的水将升高 x cm,
容器内的水的体积的算术表达:
容器内的水的体积的代数表达:
6.
1、在解决图形问题时,
要抓住用不同方法表示出来的图形面积相等这一关系列出方程即可.
2、在解决等积变形问题时,首先要找到在变化过程中不变量,
善于利用图形的面积、体积、周长及质量等捕捉等量关系,从而列出方程.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
