6.3 正方形
图片预览






文档简介
课件21张PPT。6.3正方形
平行四边形矩形菱形正方形1. 正方形的定义 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
课本P145:
回顾并思考 2.你认为正方形有哪些性质?
边: 对边平行
四边相等
角 :四个角都是直角 对角线:相等
互相垂直平分
每条对角线平分一组对角。
0D:我的文档左信举j2040600.swf正方形是轴对称图形,也是中心对称图形正方形具有平行四边形,矩形,菱形的一切性质3.如何判定一个图形是正方形呢?(可从平行四边形、矩形、菱形为基础)有一组邻边相等且有一个角是直角的平行四边形叫做正方形。 定义法有一个角是直角的菱形是正方形。有一组邻边相等的矩形是正方形。课本P145:做一做课本P146:例题(请你叙述证明思路)课本P146:课内练习思考P147:7小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质=平行四边形 性质+矩形性质+菱形性质 平行四边形,矩形,菱形,正方形之间的关系.说一说 ----下列说法对吗?
(1)四个角都相等的四边形是正方形
(2)四条边都相等的四边形是正方形
(3)对角线相等的菱形是正方形
(4)对角线互相垂直的矩形是正方形
(5)对角线垂直且相等的四边形是正方形
(6)四边相等,有一角是直角的四边形是正方形
(7) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形
(8) 正方形是轴对称图形,一共有2条对称轴辨一辨正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD例1.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.求证:四边形DEBF是正方形.证明:∵ DF⊥BC,DE⊥AB,∴ ∠DEB= ∠DFB=90°,而∠ABC=90°, ∴四边形DEBF是矩形( ), ∵ BD平分∠ABC, DF⊥BC , DE⊥AB, ∴ DE= DF( ), ∴四边形DEBF是正方形( ). 矩形的判定定理角平分线的定理正方形的判定定理
1.已知:如图点A’、B’、C’、D’
分别是正方形ABCD的四条边上的点,
并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形练一练这块纸是否也可以说是平行四边形?矩形?菱形?
与一般的平行四边形相比,它有何特殊性?
与一般的矩形相比,它有何特殊性?
与一般的菱形相比,它又有何特殊性?1.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。知识应用 2.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,如图(2)。
求:AC的长及正方形的面积S。 3.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
4.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:5.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF你说我说大家说谈谈本节课的收获
平行四边形矩形菱形正方形1. 正方形的定义 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
课本P145:
回顾并思考 2.你认为正方形有哪些性质?
边: 对边平行
四边相等
角 :四个角都是直角 对角线:相等
互相垂直平分
每条对角线平分一组对角。
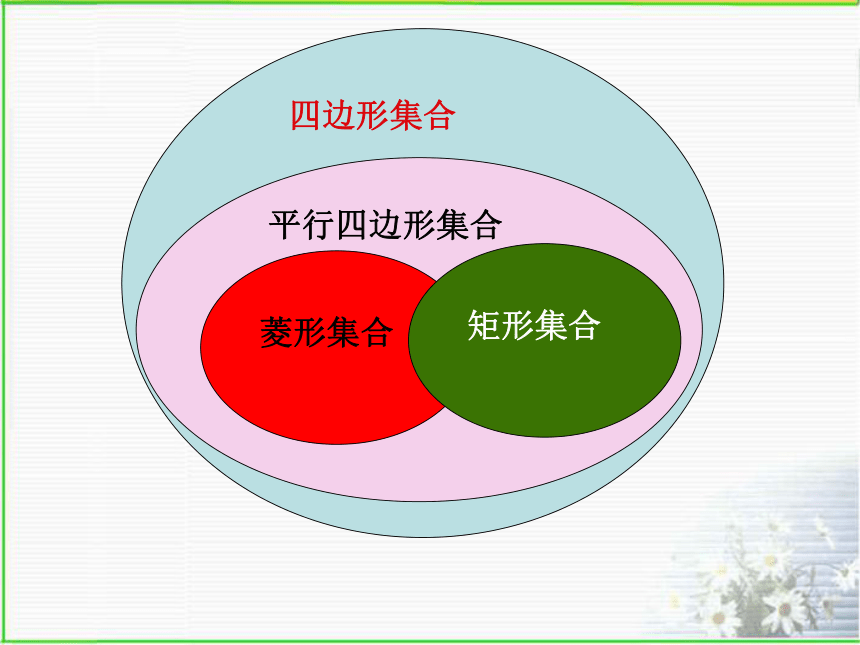
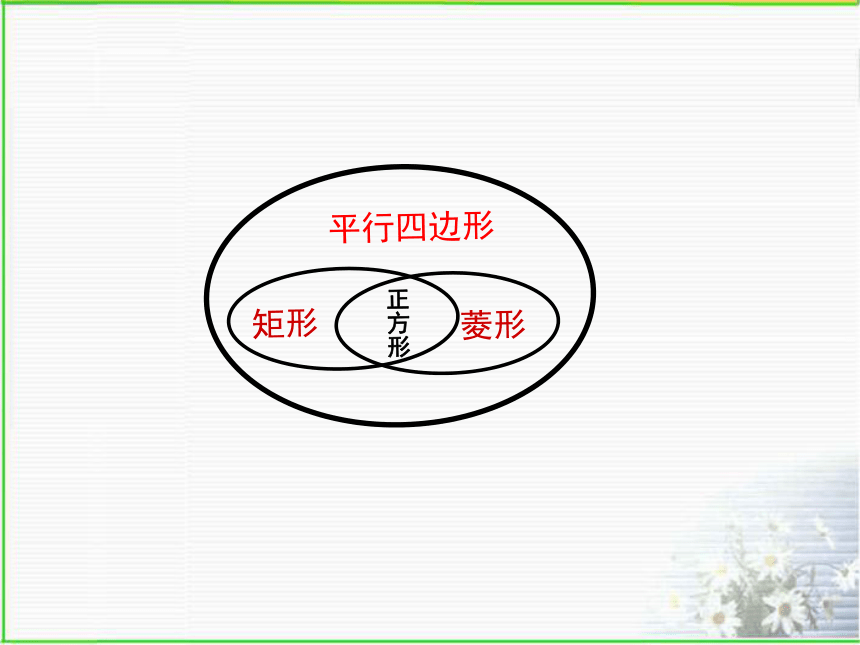
0D:我的文档左信举j2040600.swf正方形是轴对称图形,也是中心对称图形正方形具有平行四边形,矩形,菱形的一切性质3.如何判定一个图形是正方形呢?(可从平行四边形、矩形、菱形为基础)有一组邻边相等且有一个角是直角的平行四边形叫做正方形。 定义法有一个角是直角的菱形是正方形。有一组邻边相等的矩形是正方形。课本P145:做一做课本P146:例题(请你叙述证明思路)课本P146:课内练习思考P147:7小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质=平行四边形 性质+矩形性质+菱形性质 平行四边形,矩形,菱形,正方形之间的关系.说一说 ----下列说法对吗?
(1)四个角都相等的四边形是正方形
(2)四条边都相等的四边形是正方形
(3)对角线相等的菱形是正方形
(4)对角线互相垂直的矩形是正方形
(5)对角线垂直且相等的四边形是正方形
(6)四边相等,有一角是直角的四边形是正方形
(7) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形
(8) 正方形是轴对称图形,一共有2条对称轴辨一辨正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD例1.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.求证:四边形DEBF是正方形.证明:∵ DF⊥BC,DE⊥AB,∴ ∠DEB= ∠DFB=90°,而∠ABC=90°, ∴四边形DEBF是矩形( ), ∵ BD平分∠ABC, DF⊥BC , DE⊥AB, ∴ DE= DF( ), ∴四边形DEBF是正方形( ). 矩形的判定定理角平分线的定理正方形的判定定理
1.已知:如图点A’、B’、C’、D’
分别是正方形ABCD的四条边上的点,
并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形练一练这块纸是否也可以说是平行四边形?矩形?菱形?
与一般的平行四边形相比,它有何特殊性?
与一般的矩形相比,它有何特殊性?
与一般的菱形相比,它又有何特殊性?1.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。知识应用 2.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,如图(2)。
求:AC的长及正方形的面积S。 3.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
4.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:5.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF你说我说大家说谈谈本节课的收获
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
