5.4 一次函数的图象与性质 教学课件-浙教版数学八年级上册(28张ppt)
文档属性
| 名称 | 5.4 一次函数的图象与性质 教学课件-浙教版数学八年级上册(28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 20:43:31 | ||
图片预览





文档简介
(共28张PPT)
一次函数的图象与性质
年 级:八年级
学 科:初中数学(浙教版)
回顾旧知
概念:
一般地,函数y=kx+b(k,b都是常数,且k≠0)叫做一次函数.
概念
图象
一次函数
函数
应用
性质
图象
引入新知
概念:
把一个函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做这个函数的图象.
深入探究
合作学习1:画出函数y=2x的图象.
1.分别选择若干对自变量与函数的对应值,完成下表.
x … -2 -1 0 1 2 …
y=2x … …
(-2,-4),(-1,-2),(0,0),(1,2),(2,4).
2
-2
0
-4
4
2.分别以表中x的值作点的横坐标,对应的y值作纵坐标,
得到一组点,写出用坐标表示的这一组点.
3.画一个直角坐标系,并在直角坐标系中画出这组点.
4.观察所画的点,你发现了什么?
y=2x
深入探究
这种画函数图象的方法叫做描点法.
列表
描点
连线
深入探究
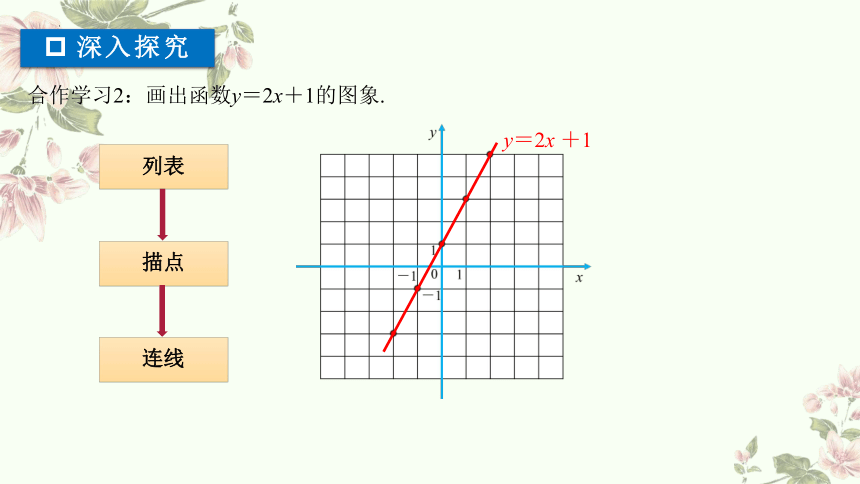
合作学习2:画出函数y=2x+1的图象.
y=2x +1
列表
描点
连线
深入探究
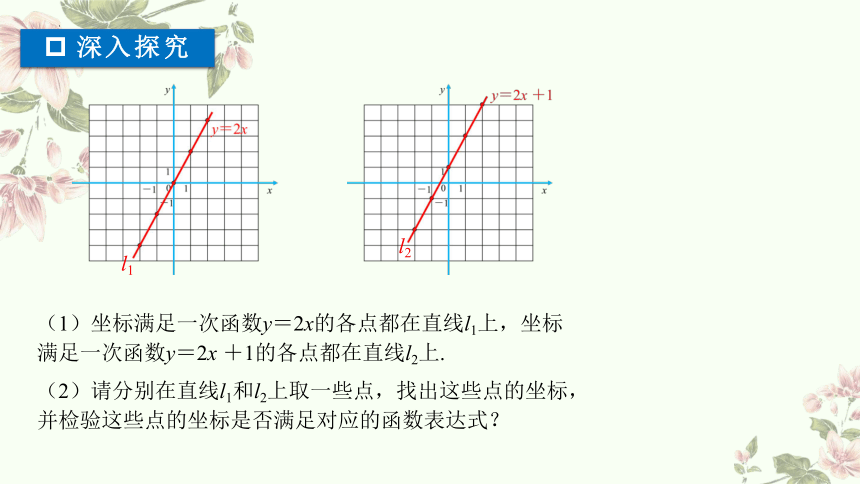
(1)坐标满足一次函数y=2x的各点都在直线l1上,坐标满足一次函数y=2x +1的各点都在直线l2上.
l1
l2
(2)请分别在直线l1和l2上取一些点,找出这些点的坐标,并检验这些点的坐标是否满足对应的函数表达式?
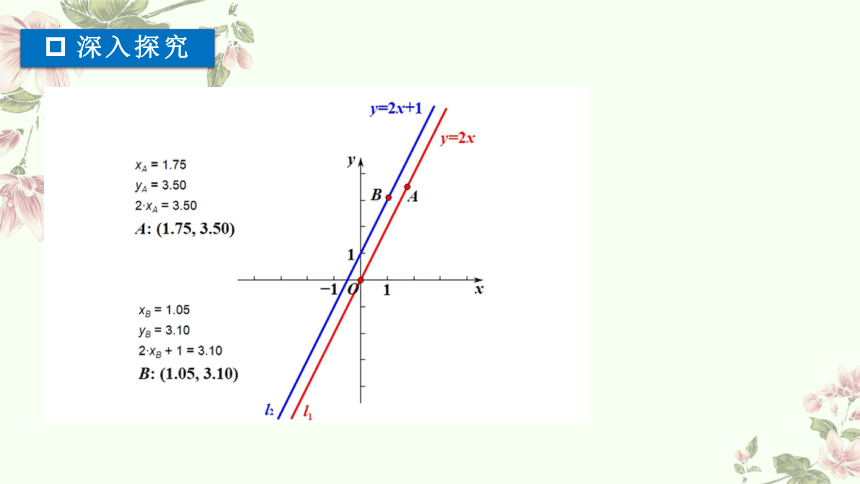
深入探究
深入探究
(1)坐标满足一次函数表达式的各点都在直线上.
(2)直线上各点的坐标都满足对应的函数表达式.
归纳发现:
一次函数y=kx+b(k,b都是常数,且k≠0)可以用直角坐标系中的一条直线来表示,这条直线也叫做一次函数y=kx+b的图象.
例题演练
例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标轴交点的坐标:y=3x, y=-3x+2.
分析 因为一次函数的图象是直线,根据两点确定一条直线,所以只要画出图象上的两个点,就能画出一次函数的图象.
解 对函数y=3x,
取x=0,得y=0,得到点(0,0);
取x=1,得y=3,得到点(1,3).
过点(0,0),(1,3)画直线,就得到函数y=3x的图象. 从图象可以看出,它与坐标轴的交点是原点(0,0).
y=3x
例题演练
例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标轴交点的坐标:y=3x, y=-3x+2.
同理 对函数y=-3x+2,
取x=0,得y=2,得到点(0,2);
取x=1,得y=-1,得到点(1,-1).
过点(0,2),(1,-1)画直线,就得到函数
y=-3x +2的图象. 从图象可以看出,它与y轴的
交点是(0,2).
取y=0,得x= ,即y=-3x +2与x轴的交点是
(,0).
y=3x
y=-3x+2
深入探究
思考 你能直接利用函数的表达式求函数图象与坐标轴交点的坐标吗?
令x=0,可得函数图象与y轴交点的纵坐标b,即图象与y轴交点的坐标为(0,b).
令y=0,可得函数图象与x轴交点的横坐标,即图象与x轴交点的坐标为( ,0).
对于一次函数y=kx+b(k,b都是常数,且k≠0).
深入探究
概念
图象
一次函数
函数
性质
应用
性质
深入探究
请大家观察以下函数图象,思考k的值对函数图象有什么影响?
请将函数图象进行分类.
深入探究
k>0
k<0
深入探究
y=2x+3
x … 0 1 2 3 4 …
y … 3 5 7 9 11 …
+1
+1
+1
+1
+2
+2
+2
+2
深入探究
x … 0 1 2 3 4 …
y … 3 1 -1 -3 -5 …
+1
+1
+1
+1
-2
-2
-2
-2
y=-2x+3
深入探究
k>0
k<0
深入探究
深入探究
k>0
当x1< x2时, y1< y2.
对于一次函数y=kx+b(k,b都是常数,且k≠0)
y随x的增大而增大
深入探究
验证:已知函数y=kx+b(k,b都是常数,且k≠0),
当k>0,x1< x2时, y1< y2.
y1- y2 =( kx1+b)-( kx2+b )
= k(x1- x2)
∵ k>0,x1< x2 ,
∴k(x1- x2)<0
∴即y1< y2.
深入探究
k>0
当x1< x2时, y1< y2.
对于一次函数y=kx+b(k,b都是常数,且k≠0)
y随x的增大而增大
k<0
当x1< x2时, y1> y2.
y随x的增大而减小
深化拓展
练习:设下列两个函数当x=x1时,y=y1;当x=x2时,y=y2 .用“>”或“<”填空.
对于函数y=x,若x2>x1,则y2_____y1;
对于函数y=﹣x+3,若x2_____x1,则y2<y1.
>
>
深化拓展
例:要从甲、乙两仓库向A、B两工地运送水泥,已知甲仓库可运出100吨水泥,乙仓库可运出80吨水泥;A工地需70吨水泥,B工地需110吨水泥,两仓库到A,B两工地的路程和每吨每千米的运费如下表:
(1)设甲仓库运往A地水泥x吨,求总运费y关于x的函数表达式,并画出图象.
深化拓展
解:(1)各仓库运出的水泥吨数和运费如表
∴ y=1.2×20x+1×25×(100-x) + 1.2×15×(70 - x)
+ 0.8×20×(10 + x) = -3x + 3920
∴y关于x的函数关系式是y=-3x + 3920(0≤x≤70),其图象如图所示.
深化拓展
解:
在一次函数y=-3x+3920(0≤x≤70)中
∵k= -3 < 0,
∴ y的值随x的增大而减小.
∵0 ≤x≤70,
∴当x=70时,y的值最小.
即当甲仓库向A,B两工地各运送70吨和30吨水泥,乙仓库不向A工地运送水泥,而只向B工地运送80吨水泥时,总运费最省,最省的总运费为-3×70+3920=3710(元).
(2)当甲、乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
小结新课
概念
图象
一次函数
函数
应用
性质
同学们再见
一次函数的图象与性质
年 级:八年级
学 科:初中数学(浙教版)
回顾旧知
概念:
一般地,函数y=kx+b(k,b都是常数,且k≠0)叫做一次函数.
概念
图象
一次函数
函数
应用
性质
图象
引入新知
概念:
把一个函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做这个函数的图象.
深入探究
合作学习1:画出函数y=2x的图象.
1.分别选择若干对自变量与函数的对应值,完成下表.
x … -2 -1 0 1 2 …
y=2x … …
(-2,-4),(-1,-2),(0,0),(1,2),(2,4).
2
-2
0
-4
4
2.分别以表中x的值作点的横坐标,对应的y值作纵坐标,
得到一组点,写出用坐标表示的这一组点.
3.画一个直角坐标系,并在直角坐标系中画出这组点.
4.观察所画的点,你发现了什么?
y=2x
深入探究
这种画函数图象的方法叫做描点法.
列表
描点
连线
深入探究
合作学习2:画出函数y=2x+1的图象.
y=2x +1
列表
描点
连线
深入探究
(1)坐标满足一次函数y=2x的各点都在直线l1上,坐标满足一次函数y=2x +1的各点都在直线l2上.
l1
l2
(2)请分别在直线l1和l2上取一些点,找出这些点的坐标,并检验这些点的坐标是否满足对应的函数表达式?
深入探究
深入探究
(1)坐标满足一次函数表达式的各点都在直线上.
(2)直线上各点的坐标都满足对应的函数表达式.
归纳发现:
一次函数y=kx+b(k,b都是常数,且k≠0)可以用直角坐标系中的一条直线来表示,这条直线也叫做一次函数y=kx+b的图象.
例题演练
例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标轴交点的坐标:y=3x, y=-3x+2.
分析 因为一次函数的图象是直线,根据两点确定一条直线,所以只要画出图象上的两个点,就能画出一次函数的图象.
解 对函数y=3x,
取x=0,得y=0,得到点(0,0);
取x=1,得y=3,得到点(1,3).
过点(0,0),(1,3)画直线,就得到函数y=3x的图象. 从图象可以看出,它与坐标轴的交点是原点(0,0).
y=3x
例题演练
例1 在同一直角坐标系中画出下列函数的图象,并求出它们与坐标轴交点的坐标:y=3x, y=-3x+2.
同理 对函数y=-3x+2,
取x=0,得y=2,得到点(0,2);
取x=1,得y=-1,得到点(1,-1).
过点(0,2),(1,-1)画直线,就得到函数
y=-3x +2的图象. 从图象可以看出,它与y轴的
交点是(0,2).
取y=0,得x= ,即y=-3x +2与x轴的交点是
(,0).
y=3x
y=-3x+2
深入探究
思考 你能直接利用函数的表达式求函数图象与坐标轴交点的坐标吗?
令x=0,可得函数图象与y轴交点的纵坐标b,即图象与y轴交点的坐标为(0,b).
令y=0,可得函数图象与x轴交点的横坐标,即图象与x轴交点的坐标为( ,0).
对于一次函数y=kx+b(k,b都是常数,且k≠0).
深入探究
概念
图象
一次函数
函数
性质
应用
性质
深入探究
请大家观察以下函数图象,思考k的值对函数图象有什么影响?
请将函数图象进行分类.
深入探究
k>0
k<0
深入探究
y=2x+3
x … 0 1 2 3 4 …
y … 3 5 7 9 11 …
+1
+1
+1
+1
+2
+2
+2
+2
深入探究
x … 0 1 2 3 4 …
y … 3 1 -1 -3 -5 …
+1
+1
+1
+1
-2
-2
-2
-2
y=-2x+3
深入探究
k>0
k<0
深入探究
深入探究
k>0
当x1< x2时, y1< y2.
对于一次函数y=kx+b(k,b都是常数,且k≠0)
y随x的增大而增大
深入探究
验证:已知函数y=kx+b(k,b都是常数,且k≠0),
当k>0,x1< x2时, y1< y2.
y1- y2 =( kx1+b)-( kx2+b )
= k(x1- x2)
∵ k>0,x1< x2 ,
∴k(x1- x2)<0
∴即y1< y2.
深入探究
k>0
当x1< x2时, y1< y2.
对于一次函数y=kx+b(k,b都是常数,且k≠0)
y随x的增大而增大
k<0
当x1< x2时, y1> y2.
y随x的增大而减小
深化拓展
练习:设下列两个函数当x=x1时,y=y1;当x=x2时,y=y2 .用“>”或“<”填空.
对于函数y=x,若x2>x1,则y2_____y1;
对于函数y=﹣x+3,若x2_____x1,则y2<y1.
>
>
深化拓展
例:要从甲、乙两仓库向A、B两工地运送水泥,已知甲仓库可运出100吨水泥,乙仓库可运出80吨水泥;A工地需70吨水泥,B工地需110吨水泥,两仓库到A,B两工地的路程和每吨每千米的运费如下表:
(1)设甲仓库运往A地水泥x吨,求总运费y关于x的函数表达式,并画出图象.
深化拓展
解:(1)各仓库运出的水泥吨数和运费如表
∴ y=1.2×20x+1×25×(100-x) + 1.2×15×(70 - x)
+ 0.8×20×(10 + x) = -3x + 3920
∴y关于x的函数关系式是y=-3x + 3920(0≤x≤70),其图象如图所示.
深化拓展
解:
在一次函数y=-3x+3920(0≤x≤70)中
∵k= -3 < 0,
∴ y的值随x的增大而减小.
∵0 ≤x≤70,
∴当x=70时,y的值最小.
即当甲仓库向A,B两工地各运送70吨和30吨水泥,乙仓库不向A工地运送水泥,而只向B工地运送80吨水泥时,总运费最省,最省的总运费为-3×70+3920=3710(元).
(2)当甲、乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
小结新课
概念
图象
一次函数
函数
应用
性质
同学们再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
