5.4 一元一次方程的解法(第1课时 移项、去括号)课件(共31张PPT)
文档属性
| 名称 | 5.4 一元一次方程的解法(第1课时 移项、去括号)课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 06:47:36 | ||
图片预览










文档简介
(共31张PPT)
5.4 一元一次方程的解法
浙教版(2024) 七年级数学上册 第五章 一元一次方程
第一课时 移项、去括号
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 学生能熟练掌握移项、合并同类项等解一元一次方程的基本步骤;
2. 能够准确求解各种类型的一元一次方程,包括含括号、分数系数的方程;
3. 通过方程求解,培养学生的逻辑思维和数学运算能力,提高解决实际问题的能力。
情景导入
比较如图左、右两个天平,你发现了什么?
方程两边同时减去3x,方程仍然成立。
新知探究
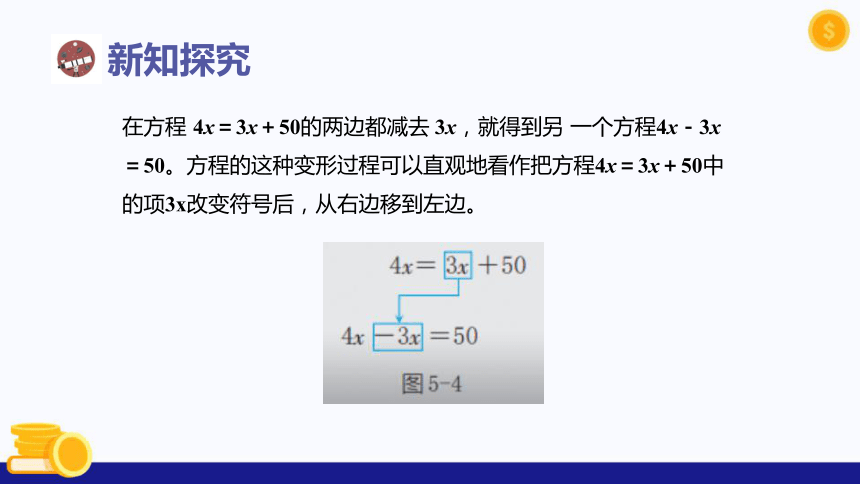
在方程 4x=3x+50的两边都减去 3x,就得到另 一个方程4x-3x=50。方程的这种变形过程可以直观地看作把方程4x=3x+50中的项3x改变符号后,从右边移到左边。
概念归纳
一般地,把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫作移项.
移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边。
课本例题
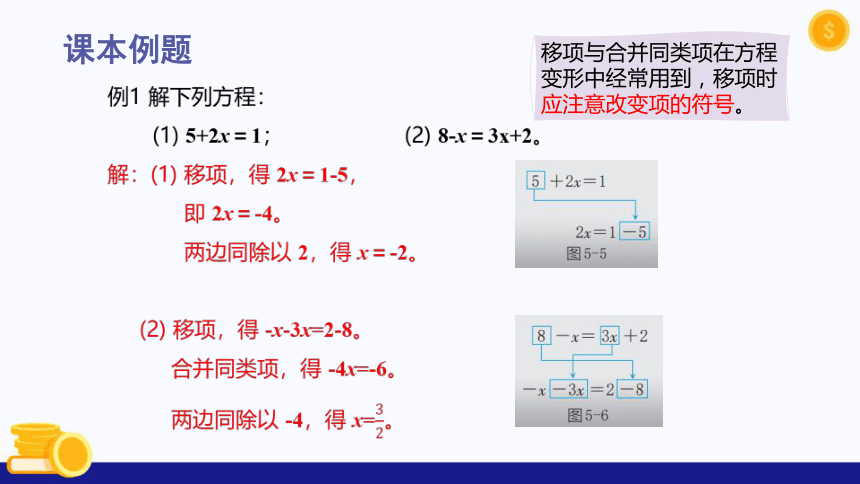
例1 解下列方程:
(1) 5+2x=1; (2) 8-x=3x+2。
解:(1) 移项,得 2x=1-5,
即 2x=-4。
两边同除以 2,得 x=-2。
(2) 移项,得 -x-3x=2-8。
合并同类项,得 -4x=-6。
两边同除以 -4,得 x=。
移项与合并同类项在方程变形中经常用到,移项时应注意改变项的符号。
课本例题
例2 解下列方程:
(1) 3-(4x-5)=9; (2) 2x-2=3(x+1) (结果精确到0.01)。
分析:当方程中的一边或两边有括号时,我们往往先去掉括号,再进行移项、合并同类项等变形求解。
解:(1)去括号,得 3-4x+5=9。
移项,得 -4x=9-5-3。
合并同类项,得 -4x=1。
两边同除以 -4,得 x=-。
解:(2) 去括号,得 2x-3x+3。
移项,得 2x-3x=3+。
合并同类项,得 -x=3+ ,
即 x=-(3+ 。
所以 x ≈ -4.41。
(2) 2x-2=3(x+1) (结果精确到0.01)。
课本练习
解下列方程:
3. 下列变形对吗?若不对,请说明理由,并改正。
解方程:3-2(0.2x+1)= x。
解:去括号,得 3-0.4x+2=0.2x。
移项,得 -0.4x+0.2x=-3-2。
合并同类项,得 -0.2x=-5。
两边同除以 -0.2,得 x=25。
解:不对,去括号和移项时各有一项没变号。
改正:去括号,得 3-0.4x-2=0.2x。
移项,得 -0.4x-0.2x=-3+2。
合并同类项,得 -0.6x=-1。
两边同除以 -0.6,得 x= 。
分层练习-基础
知识点1 利用移项解一元一次方程
1. 方程5x+4=2x-5移项后,正确的是( B )
A. 5x+2x=4-5 B. 5x-2x=-5-4
C. 5x-2x=4-5 D. 5x+2x=-5-4
B
2. [2023·衢州衢江区期末]如图,将方程4x=3x+50进行移
项,则“ ”处应填写的是 .
3. 关于x的方程3x+6=0的解与方程3x+2a=-1的解相
同,则a的值是 .
-3x
4. 解下列方程:
(1)7y+6=-6y;
【解】移项,得7y+6y=-6,
合并同类项,得13y=-6,解得y=- ;
移项,得5x-7x=8-2,
合并同类项,得-2x=6,解得x=-3;
(2)5x+2=7x+8;
移项,得3y-y-6y=1+2,
合并同类项,得-4y=3,解得y=- ;
移项,得 x+ x=8+ ,
合并同类项,得 x= ,解得x= .
(3)3y-2=y+1+6y;
(4) x-8= - x.
知识点2 利用去括号解一元一次方程
5. 方程7(3-x)-5(x-3)=5去括号,正确的是( C )
A. 21-x-5x+15=5
B. 21-7x-5x-15=5
C. 21-7x-5x+15=5
D. 21-x-5x-15=5
C
6. 若代数式12-3(9-y)与代数式5(y-4)的值相等,则y
= .
7. [2024·深圳龙岗区二模]若关于x的方程3x+2a=2(x-b)
的解是x=-6,则a+b的值是 .
3
8. 解方程:
(1)x+2(3x-1)=3(x-4);
【解】去括号,得x+6x-2=3x-12,
移项,得x+6x-3x=-12+2,
合并同类项,得4x=-10,解得x=- .
(2)5(x-2)-1=-2(2x+1);
【解】去括号,得5x-10-1=-4x-2,
移项,得5x+4x=-2+10+1,
合并同类项,得9x=9,解得x=1.
(3)9x-4(0.5x+2)=2(3x+0.5).
【解】去括号,得9x-2x-8=6x+1,
移项,得9x-2x-6x=1+8,
合并同类项,得x=9.
[易错题]去括号时未改变符号或漏乘而出错
9. [母题 教材P138练习T3]老师在黑板上出了一道解方程的题2(x+3)-3(x-1)=5(1-x),小明马上举手,要求到黑板上做,他是这样做的:解:去括号,得2x+3-3x-3=5-5x,①
合并,得-x=5-5x,②
移项,得-x+5x=5,③
合并同类项,得4x=5,④
两边都除以4,得x= .⑤
小明对于解一元一次方程的一般步骤他都知道,却没有掌握好,因此解题时出现了错误.请你指出他的错误,并细心地解方程.
【解】第①步去括号有误.
正确解法:去括号,得2x+6-3x+3=5-5x,
移项,得2x-3x+5x=5-3-6,
合并同类项,得4x=-4,
解得x=-1.
分层练习-巩固
10. [2024·杭州期末]规定新运算“@”:对于任意数m,n
都有m@n=mn-m+n,例如:2@3=2×3-2+3.
若2@(x-1)的运算结果与(x-1)@2的运算结果相同,则
x的值为( C )
A. 1 B. 2 C. 3 D. 4
C
11. 七年级一班的马虎同学在解关于x的方程3a-x=13
时,误将-x看成+x,得方程的解为x=-2,则原方
程正确的解为( B )
A. x=-2 B. x=2
C. x=- D. x=
B
12. [2024·宁波鄞州区期末]若x=2是关于x的一元一次方程
mx-n=3的解,则4-6m+3n的值是 .
-5
魔术师立刻说出观众想的那个数.
如果小聪想了一个数并告诉魔术师结果为2 024,那么魔
术师立刻说出小聪想的那个数是 .
2 019
13. 魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:
14. 关于x的方程4x+2m=3x+1和方程3x+2m=4x+1的解相同,则代数式(-2m)2 026- 的值为 .
2
(1)(-3) 2的值为 .
(2)当(2 2x) (-3x)=2时,求x的值.
【解】由题意,得2 2x=2×2-3×2x=4-6x.
(4-6x) (-3x)=2(4-6x)-3×(-3x)=8-12x+9x=2.
解得x=2.
-12
15. [新视角·新定义题]已知a,b是有理数,定义一种新运
算“ ”,满足a b=2a-3b.
分层练习-拓展
16. [新视角·新定义题]定义:关于x的方程ax-b=0与方程bx-a=0(a,b均为不等于0的常数)互为“反对方程”.例如:方程2x-3=0与方程3x-2=0互为“反对方程”.
(1)【定义理解】若方程4x-1=0与方程x-m=0互为
“反对方程”,则m= .
4
(2)【知识应用】若关于x的方程4x+2m+1=0与方程
5x-(3n-2)=0互为“反对方程”,求m,n的值.
【解】因为关于x的方程4x+2m+1=0与方程5x-(3n-2)=0互为“反对方程”,
所以3n-2=4,-(2m+1)=5,
解得n=2,m=-3.
(3)【拓展提高】若关于x的方程3x+2b-1=0与其“反
对方程”的解都是整数,直接写出常数b的值.
【解】b=-1或b=2.
课堂小结
1. 一般地,把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫作移项。
2. 移项的方法:通常把含有未知数的项移到等号的左边,把常数项移到等号的右边。
3. 去括号解一元一次方程的步骤
①去括号;②移项;③合并同类项;④系数化为1.
5.4 一元一次方程的解法
浙教版(2024) 七年级数学上册 第五章 一元一次方程
第一课时 移项、去括号
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 学生能熟练掌握移项、合并同类项等解一元一次方程的基本步骤;
2. 能够准确求解各种类型的一元一次方程,包括含括号、分数系数的方程;
3. 通过方程求解,培养学生的逻辑思维和数学运算能力,提高解决实际问题的能力。
情景导入
比较如图左、右两个天平,你发现了什么?
方程两边同时减去3x,方程仍然成立。
新知探究
在方程 4x=3x+50的两边都减去 3x,就得到另 一个方程4x-3x=50。方程的这种变形过程可以直观地看作把方程4x=3x+50中的项3x改变符号后,从右边移到左边。
概念归纳
一般地,把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫作移项.
移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边。
课本例题
例1 解下列方程:
(1) 5+2x=1; (2) 8-x=3x+2。
解:(1) 移项,得 2x=1-5,
即 2x=-4。
两边同除以 2,得 x=-2。
(2) 移项,得 -x-3x=2-8。
合并同类项,得 -4x=-6。
两边同除以 -4,得 x=。
移项与合并同类项在方程变形中经常用到,移项时应注意改变项的符号。
课本例题
例2 解下列方程:
(1) 3-(4x-5)=9; (2) 2x-2=3(x+1) (结果精确到0.01)。
分析:当方程中的一边或两边有括号时,我们往往先去掉括号,再进行移项、合并同类项等变形求解。
解:(1)去括号,得 3-4x+5=9。
移项,得 -4x=9-5-3。
合并同类项,得 -4x=1。
两边同除以 -4,得 x=-。
解:(2) 去括号,得 2x-3x+3。
移项,得 2x-3x=3+。
合并同类项,得 -x=3+ ,
即 x=-(3+ 。
所以 x ≈ -4.41。
(2) 2x-2=3(x+1) (结果精确到0.01)。
课本练习
解下列方程:
3. 下列变形对吗?若不对,请说明理由,并改正。
解方程:3-2(0.2x+1)= x。
解:去括号,得 3-0.4x+2=0.2x。
移项,得 -0.4x+0.2x=-3-2。
合并同类项,得 -0.2x=-5。
两边同除以 -0.2,得 x=25。
解:不对,去括号和移项时各有一项没变号。
改正:去括号,得 3-0.4x-2=0.2x。
移项,得 -0.4x-0.2x=-3+2。
合并同类项,得 -0.6x=-1。
两边同除以 -0.6,得 x= 。
分层练习-基础
知识点1 利用移项解一元一次方程
1. 方程5x+4=2x-5移项后,正确的是( B )
A. 5x+2x=4-5 B. 5x-2x=-5-4
C. 5x-2x=4-5 D. 5x+2x=-5-4
B
2. [2023·衢州衢江区期末]如图,将方程4x=3x+50进行移
项,则“ ”处应填写的是 .
3. 关于x的方程3x+6=0的解与方程3x+2a=-1的解相
同,则a的值是 .
-3x
4. 解下列方程:
(1)7y+6=-6y;
【解】移项,得7y+6y=-6,
合并同类项,得13y=-6,解得y=- ;
移项,得5x-7x=8-2,
合并同类项,得-2x=6,解得x=-3;
(2)5x+2=7x+8;
移项,得3y-y-6y=1+2,
合并同类项,得-4y=3,解得y=- ;
移项,得 x+ x=8+ ,
合并同类项,得 x= ,解得x= .
(3)3y-2=y+1+6y;
(4) x-8= - x.
知识点2 利用去括号解一元一次方程
5. 方程7(3-x)-5(x-3)=5去括号,正确的是( C )
A. 21-x-5x+15=5
B. 21-7x-5x-15=5
C. 21-7x-5x+15=5
D. 21-x-5x-15=5
C
6. 若代数式12-3(9-y)与代数式5(y-4)的值相等,则y
= .
7. [2024·深圳龙岗区二模]若关于x的方程3x+2a=2(x-b)
的解是x=-6,则a+b的值是 .
3
8. 解方程:
(1)x+2(3x-1)=3(x-4);
【解】去括号,得x+6x-2=3x-12,
移项,得x+6x-3x=-12+2,
合并同类项,得4x=-10,解得x=- .
(2)5(x-2)-1=-2(2x+1);
【解】去括号,得5x-10-1=-4x-2,
移项,得5x+4x=-2+10+1,
合并同类项,得9x=9,解得x=1.
(3)9x-4(0.5x+2)=2(3x+0.5).
【解】去括号,得9x-2x-8=6x+1,
移项,得9x-2x-6x=1+8,
合并同类项,得x=9.
[易错题]去括号时未改变符号或漏乘而出错
9. [母题 教材P138练习T3]老师在黑板上出了一道解方程的题2(x+3)-3(x-1)=5(1-x),小明马上举手,要求到黑板上做,他是这样做的:解:去括号,得2x+3-3x-3=5-5x,①
合并,得-x=5-5x,②
移项,得-x+5x=5,③
合并同类项,得4x=5,④
两边都除以4,得x= .⑤
小明对于解一元一次方程的一般步骤他都知道,却没有掌握好,因此解题时出现了错误.请你指出他的错误,并细心地解方程.
【解】第①步去括号有误.
正确解法:去括号,得2x+6-3x+3=5-5x,
移项,得2x-3x+5x=5-3-6,
合并同类项,得4x=-4,
解得x=-1.
分层练习-巩固
10. [2024·杭州期末]规定新运算“@”:对于任意数m,n
都有m@n=mn-m+n,例如:2@3=2×3-2+3.
若2@(x-1)的运算结果与(x-1)@2的运算结果相同,则
x的值为( C )
A. 1 B. 2 C. 3 D. 4
C
11. 七年级一班的马虎同学在解关于x的方程3a-x=13
时,误将-x看成+x,得方程的解为x=-2,则原方
程正确的解为( B )
A. x=-2 B. x=2
C. x=- D. x=
B
12. [2024·宁波鄞州区期末]若x=2是关于x的一元一次方程
mx-n=3的解,则4-6m+3n的值是 .
-5
魔术师立刻说出观众想的那个数.
如果小聪想了一个数并告诉魔术师结果为2 024,那么魔
术师立刻说出小聪想的那个数是 .
2 019
13. 魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:
14. 关于x的方程4x+2m=3x+1和方程3x+2m=4x+1的解相同,则代数式(-2m)2 026- 的值为 .
2
(1)(-3) 2的值为 .
(2)当(2 2x) (-3x)=2时,求x的值.
【解】由题意,得2 2x=2×2-3×2x=4-6x.
(4-6x) (-3x)=2(4-6x)-3×(-3x)=8-12x+9x=2.
解得x=2.
-12
15. [新视角·新定义题]已知a,b是有理数,定义一种新运
算“ ”,满足a b=2a-3b.
分层练习-拓展
16. [新视角·新定义题]定义:关于x的方程ax-b=0与方程bx-a=0(a,b均为不等于0的常数)互为“反对方程”.例如:方程2x-3=0与方程3x-2=0互为“反对方程”.
(1)【定义理解】若方程4x-1=0与方程x-m=0互为
“反对方程”,则m= .
4
(2)【知识应用】若关于x的方程4x+2m+1=0与方程
5x-(3n-2)=0互为“反对方程”,求m,n的值.
【解】因为关于x的方程4x+2m+1=0与方程5x-(3n-2)=0互为“反对方程”,
所以3n-2=4,-(2m+1)=5,
解得n=2,m=-3.
(3)【拓展提高】若关于x的方程3x+2b-1=0与其“反
对方程”的解都是整数,直接写出常数b的值.
【解】b=-1或b=2.
课堂小结
1. 一般地,把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫作移项。
2. 移项的方法:通常把含有未知数的项移到等号的左边,把常数项移到等号的右边。
3. 去括号解一元一次方程的步骤
①去括号;②移项;③合并同类项;④系数化为1.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
