浙教版七年级上册数学 第5章 一元一次方程 练习(含答案)
文档属性
| 名称 | 浙教版七年级上册数学 第5章 一元一次方程 练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 22:35:36 | ||
图片预览


文档简介
浙教版七年级上册数学第五章练习
一、选择题
1.有下列各式:①m=1;②x+3x=4;③6x-7>0;④2x+y;⑤+2x=5;⑥x3y+2x=6其中是方程的有( )
A.①②④⑤ B.②③⑤⑥ C.②④⑤⑥ D.①②⑤⑥
2.根据等式的性质,下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.,则
3.检验: x = 1 是下列哪个方程的解( )
A. B. C. D.
4.把方程 去分母正确的是( )
A. B.
C. D.
5.若 与是同一个正数的两个平方根,则m的值为( )
A.3 B. C.1 D.
6.按如图所示的程序进行计算,若输入的值是3,则输出的值为1.若输出的值为3,则输入的值是( )
A. B. C.7或 D.或
7.元朝朱世杰所著的算学启蒙中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行里,慢马每天行里,慢马先行天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )
A. B.
C. D.
8.若关于x的一元一次方程 的解为x=-2,则关于y的一元一次方程 的解为( )
A.y=1 B.y=-2 C.y=-3 D.y=-4
9.如图,将甲量筒中液体全部倒入空量筒乙中,液体的高度比原来增加了5cm,根据图中的信息,可得正确的方程是 ( )
A. B.
C. D.
10.把9个数填入3×3的方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中a的值为( )
A.2 B.4 C.6 D.1
二、填空题
11.请写出一个解为 x=3 的一元一次方程 .
12.若代数式与的值互为倒数,则 .
13.若关于的方程与的解相同,则的值是 .
14.《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱.问合伙人数是多少?为解决此问题,设合伙人数为x人,可列方程为 .
15.小华做这样一道题“计算”,其中*表示被墨水染黑看不清的一个数,他翻开后面的答案得知该题的结果为7,那么*表示的数是 .
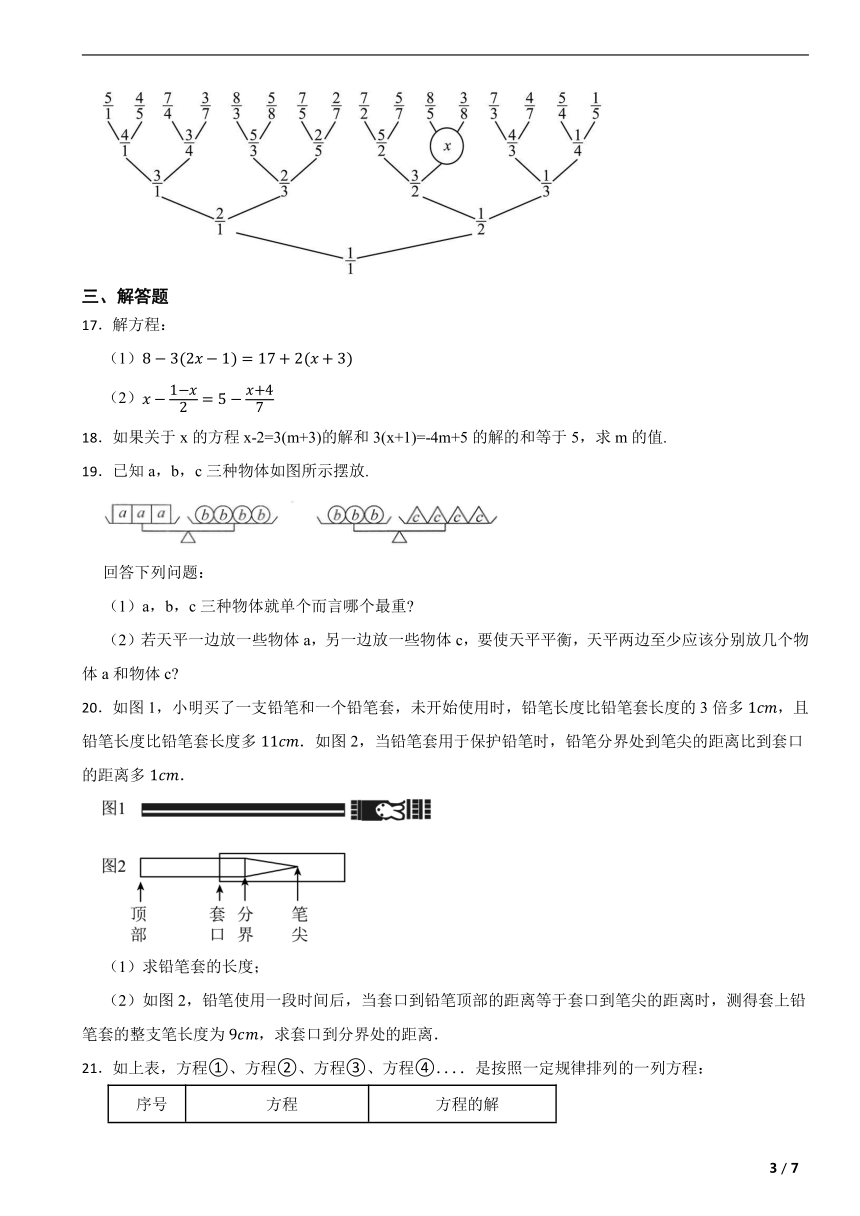
16.十九世纪与两人发明了“一棵树”,称之为“有理数树”,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,…,按照这个规律,图中所表示的数为 ;若数(,均为正整数)位于第9层,且,则表示的数为 .
三、解答题
17.解方程:
(1)
(2)
18.如果关于x的方程x-2=3(m+3)的解和3(x+1)=-4m+5的解的和等于5,求m的值.
19.已知a,b,c三种物体如图所示摆放.
回答下列问题:
(1)a,b,c三种物体就单个而言哪个最重
(2)若天平一边放一些物体a,另一边放一些物体c,要使天平平衡,天平两边至少应该分别放几个物体a和物体c
20.如图1,小明买了一支铅笔和一个铅笔套,未开始使用时,铅笔长度比铅笔套长度的3倍多,且铅笔长度比铅笔套长度多.如图2,当铅笔套用于保护铅笔时,铅笔分界处到笔尖的距离比到套口的距离多.
(1)求铅笔套的长度;
(2)如图2,铅笔使用一段时间后,当套口到铅笔顶部的距离等于套口到笔尖的距离时,测得套上铅笔套的整支笔长度为,求套口到分界处的距离.
21.如上表,方程①、方程②、方程③、方程④....是按照一定规律排列的一列方程:
序号 方程 方程的解
①
②
③ ______
④ _____
… … …
(1)将上表补充完整,
(2)按上述方程所包含的某种规律写出方程⑤及其解;
(3)写出表内这列方程中的第n(n为正整数)个方程和它的解.
22.【阅读材料】规定:若关于的一元一次方程的解为,则称该方程为“和谐方程”.
例如:方程的解为,
而,
所以方程为“和谐方程”.
请根据上述规定解答下列问题:
(1)下列关于的一元一次方程是“和谐方程”的有______;(填写序号)
①;②;③.
(2)已知关于的一元一次方程是“和谐方程”,求的值;
(3)已知关于的一元一次方程是“和谐方程”,并且它的解是,求,的值.
23.学校10月19日举办体育文化艺术节活动,准备单色圆珠笔、双色圆珠笔、三色圆珠笔三种圆珠笔共1000支作奖励(每种圆珠笔都要有),其中双色圆珠笔的单价比单色圆珠笔的单价贵0.2元,买5支双色圆珠笔和8支单色圆珠笔共需要6.2元.
(1)双色圆珠笔和单色圆珠笔的单价分别是多少元?
(2)若某超市的三色圆珠笔根据球珠直径有两个级别,学校只能从中选择一个级别.价格如下表:
三色圆珠笔级别 球珠直径 球珠直径
单价 1元 1.5元
现在学校用880元去购买这三种圆珠笔,且单色圆珠笔和三色圆珠笔的数量是相同的,应该选样哪种级别的三色圆珠笔比较合适?购买方案是什么?请说明理由.
(3)若要求购买三色圆珠笔的数量是单色圆珠笔的一半,单色圆珠笔和双色圆珠笔单价不变,其中三色圆珠笔单价为a元,在总数量不变的前提之下,无论这三种圆珠笔的数量如何分配,总费用始终不变.求此时a的值和总费用.
参考答案
1.D
2.C
3.D
4.B
5.D
解:∵ 与是同一个正数的两个平方根,
∴ 与互为相反数,
∴,
∴,
6.A
7.D
8.C
解:∵关于x的一元一次方程 的解为x=-2
∴关于y的一元一次方程 的解为y+1=-2
∴y=-2-1=-3
9.B
解:由圆柱的体积公式,可得大量筒中水的体积为:,小量筒中水的体积为:;根据大量筒中水的体积等于小量筒中水的体积,可列出方程:.
10.D
11.2x=6
12.
13.
解:解方程2x 1=3,得:x=2,
把x=2代入方程,得,
解得:a=.
14.
解:设合伙人数为x人,由题意得,
15.或3
解:设所表示的数为x,则
|(-4)-x|=7
∴-4-x=7或-4-x=-7,
∴x=-11或3.
即所表示的数为-11或3.
16.;
17.(1)
(2)
18.解:解方程x-2=3(m+3),
得x=3m+11
解方程3(x+1)=-4m+5,
得
∴3m+11+
解得m=-4.
19.(1)解:由图可得:3a=4b,3b=4c
∴3a=4b,等式两边同时除以3,得a=43b,
3b=4c,等式两边同时除以4,得34b=c.
∵43b>b>34b
∴a>b﹥c
∴ a,b,c三种物体就单个而言a最重.
(2)解:∵3a=4b,3b=4c
∴b=34a,b=43c
∴34a=43c
∴9a=16c
∴若天平一边放一些物体a,另一边放一些物体c、要使天平平衡,天平一边至少放9个物体a,天平另一边至少放16个物体c
20.(1)铅笔套的长度为
(2)套口到分界处的距离为
21.(1),
(2)
(3)
22.(1)②
(2)
(3)
23.(1)解:设单色圆珠笔单价为元,双色圆珠笔单价为 元,由题意得:,解得,∴,
答:单色圆珠笔单价为元,双色圆珠笔单价为元.
(2)解:设购买单色圆珠笔支,三色圆珠笔支,则双色圆珠笔支,当选球珠直径三色圆珠笔购买时,
则,
解得,不合题意;
当选球珠直径三色圆珠笔购买时,
则,
解得,
∴,符合题意,
答:购买单色圆珠笔和三色圆珠笔各支,双色圆珠笔支.
(3)解:设购买支三色圆珠笔,则单色圆珠笔支,双色圆珠笔支,总费用为元,由题意得:
,
∵与无关,∴,解得:,∴,
答:此时的值为,总费用始终不变,总费用为元.
1 / 1
一、选择题
1.有下列各式:①m=1;②x+3x=4;③6x-7>0;④2x+y;⑤+2x=5;⑥x3y+2x=6其中是方程的有( )
A.①②④⑤ B.②③⑤⑥ C.②④⑤⑥ D.①②⑤⑥
2.根据等式的性质,下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.,则
3.检验: x = 1 是下列哪个方程的解( )
A. B. C. D.
4.把方程 去分母正确的是( )
A. B.
C. D.
5.若 与是同一个正数的两个平方根,则m的值为( )
A.3 B. C.1 D.
6.按如图所示的程序进行计算,若输入的值是3,则输出的值为1.若输出的值为3,则输入的值是( )
A. B. C.7或 D.或
7.元朝朱世杰所著的算学启蒙中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行里,慢马每天行里,慢马先行天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )
A. B.
C. D.
8.若关于x的一元一次方程 的解为x=-2,则关于y的一元一次方程 的解为( )
A.y=1 B.y=-2 C.y=-3 D.y=-4
9.如图,将甲量筒中液体全部倒入空量筒乙中,液体的高度比原来增加了5cm,根据图中的信息,可得正确的方程是 ( )
A. B.
C. D.
10.把9个数填入3×3的方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中a的值为( )
A.2 B.4 C.6 D.1
二、填空题
11.请写出一个解为 x=3 的一元一次方程 .
12.若代数式与的值互为倒数,则 .
13.若关于的方程与的解相同,则的值是 .
14.《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱.问合伙人数是多少?为解决此问题,设合伙人数为x人,可列方程为 .
15.小华做这样一道题“计算”,其中*表示被墨水染黑看不清的一个数,他翻开后面的答案得知该题的结果为7,那么*表示的数是 .
16.十九世纪与两人发明了“一棵树”,称之为“有理数树”,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,…,按照这个规律,图中所表示的数为 ;若数(,均为正整数)位于第9层,且,则表示的数为 .
三、解答题
17.解方程:
(1)
(2)
18.如果关于x的方程x-2=3(m+3)的解和3(x+1)=-4m+5的解的和等于5,求m的值.
19.已知a,b,c三种物体如图所示摆放.
回答下列问题:
(1)a,b,c三种物体就单个而言哪个最重
(2)若天平一边放一些物体a,另一边放一些物体c,要使天平平衡,天平两边至少应该分别放几个物体a和物体c
20.如图1,小明买了一支铅笔和一个铅笔套,未开始使用时,铅笔长度比铅笔套长度的3倍多,且铅笔长度比铅笔套长度多.如图2,当铅笔套用于保护铅笔时,铅笔分界处到笔尖的距离比到套口的距离多.
(1)求铅笔套的长度;
(2)如图2,铅笔使用一段时间后,当套口到铅笔顶部的距离等于套口到笔尖的距离时,测得套上铅笔套的整支笔长度为,求套口到分界处的距离.
21.如上表,方程①、方程②、方程③、方程④....是按照一定规律排列的一列方程:
序号 方程 方程的解
①
②
③ ______
④ _____
… … …
(1)将上表补充完整,
(2)按上述方程所包含的某种规律写出方程⑤及其解;
(3)写出表内这列方程中的第n(n为正整数)个方程和它的解.
22.【阅读材料】规定:若关于的一元一次方程的解为,则称该方程为“和谐方程”.
例如:方程的解为,
而,
所以方程为“和谐方程”.
请根据上述规定解答下列问题:
(1)下列关于的一元一次方程是“和谐方程”的有______;(填写序号)
①;②;③.
(2)已知关于的一元一次方程是“和谐方程”,求的值;
(3)已知关于的一元一次方程是“和谐方程”,并且它的解是,求,的值.
23.学校10月19日举办体育文化艺术节活动,准备单色圆珠笔、双色圆珠笔、三色圆珠笔三种圆珠笔共1000支作奖励(每种圆珠笔都要有),其中双色圆珠笔的单价比单色圆珠笔的单价贵0.2元,买5支双色圆珠笔和8支单色圆珠笔共需要6.2元.
(1)双色圆珠笔和单色圆珠笔的单价分别是多少元?
(2)若某超市的三色圆珠笔根据球珠直径有两个级别,学校只能从中选择一个级别.价格如下表:
三色圆珠笔级别 球珠直径 球珠直径
单价 1元 1.5元
现在学校用880元去购买这三种圆珠笔,且单色圆珠笔和三色圆珠笔的数量是相同的,应该选样哪种级别的三色圆珠笔比较合适?购买方案是什么?请说明理由.
(3)若要求购买三色圆珠笔的数量是单色圆珠笔的一半,单色圆珠笔和双色圆珠笔单价不变,其中三色圆珠笔单价为a元,在总数量不变的前提之下,无论这三种圆珠笔的数量如何分配,总费用始终不变.求此时a的值和总费用.
参考答案
1.D
2.C
3.D
4.B
5.D
解:∵ 与是同一个正数的两个平方根,
∴ 与互为相反数,
∴,
∴,
6.A
7.D
8.C
解:∵关于x的一元一次方程 的解为x=-2
∴关于y的一元一次方程 的解为y+1=-2
∴y=-2-1=-3
9.B
解:由圆柱的体积公式,可得大量筒中水的体积为:,小量筒中水的体积为:;根据大量筒中水的体积等于小量筒中水的体积,可列出方程:.
10.D
11.2x=6
12.
13.
解:解方程2x 1=3,得:x=2,
把x=2代入方程,得,
解得:a=.
14.
解:设合伙人数为x人,由题意得,
15.或3
解:设所表示的数为x,则
|(-4)-x|=7
∴-4-x=7或-4-x=-7,
∴x=-11或3.
即所表示的数为-11或3.
16.;
17.(1)
(2)
18.解:解方程x-2=3(m+3),
得x=3m+11
解方程3(x+1)=-4m+5,
得
∴3m+11+
解得m=-4.
19.(1)解:由图可得:3a=4b,3b=4c
∴3a=4b,等式两边同时除以3,得a=43b,
3b=4c,等式两边同时除以4,得34b=c.
∵43b>b>34b
∴a>b﹥c
∴ a,b,c三种物体就单个而言a最重.
(2)解:∵3a=4b,3b=4c
∴b=34a,b=43c
∴34a=43c
∴9a=16c
∴若天平一边放一些物体a,另一边放一些物体c、要使天平平衡,天平一边至少放9个物体a,天平另一边至少放16个物体c
20.(1)铅笔套的长度为
(2)套口到分界处的距离为
21.(1),
(2)
(3)
22.(1)②
(2)
(3)
23.(1)解:设单色圆珠笔单价为元,双色圆珠笔单价为 元,由题意得:,解得,∴,
答:单色圆珠笔单价为元,双色圆珠笔单价为元.
(2)解:设购买单色圆珠笔支,三色圆珠笔支,则双色圆珠笔支,当选球珠直径三色圆珠笔购买时,
则,
解得,不合题意;
当选球珠直径三色圆珠笔购买时,
则,
解得,
∴,符合题意,
答:购买单色圆珠笔和三色圆珠笔各支,双色圆珠笔支.
(3)解:设购买支三色圆珠笔,则单色圆珠笔支,双色圆珠笔支,总费用为元,由题意得:
,
∵与无关,∴,解得:,∴,
答:此时的值为,总费用始终不变,总费用为元.
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
