一次函数与平行四边形专项练习(含解析)
文档属性
| 名称 | 一次函数与平行四边形专项练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 499.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
一次函数与平行四边形 专项练习
一.选择题(共1小题)
1.若函数y=(m+1)x|m|﹣5是一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.0
二.填空题(共8小题)
2.直线y1=ax与直线在同一平面直角坐标系中的图象如图所示,关于x的不等式的解集为 .
3.如图,已知函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),则不等式ax+b≤kx﹣3的解集是 .
4.根据图象,可得关于x的不等式kx<﹣x+3的解集是 .
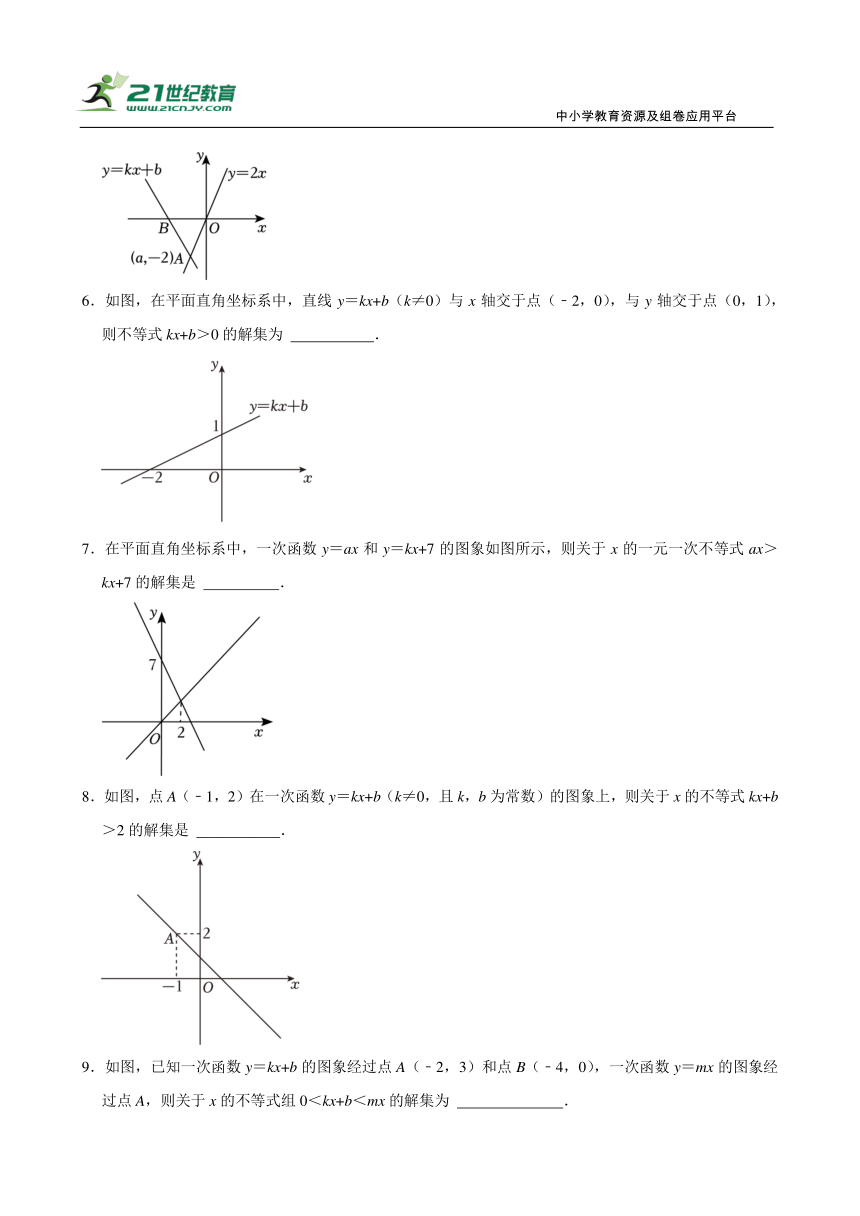
5.如图,一次函数y=kx+b(k≠0)的图象经过点A(a,﹣2),一次函数y=2x的图象过点A,则不等式2x≤kx+b的解集为 .
6.如图,在平面直角坐标系中,直线y=kx+b(k≠0)与x轴交于点(﹣2,0),与y轴交于点(0,1),则不等式kx+b>0的解集为 .
7.在平面直角坐标系中,一次函数y=ax和y=kx+7的图象如图所示,则关于x的一元一次不等式ax>kx+7的解集是 .
8.如图,点A(﹣1,2)在一次函数y=kx+b(k≠0,且k,b为常数)的图象上,则关于x的不等式kx+b>2的解集是 .
9.如图,已知一次函数y=kx+b的图象经过点A(﹣2,3)和点B(﹣4,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为 .
三.解答题(共16小题)
10.如图,一次函数y=kx+b(k≠0)的图象过点A(﹣2,2),B(2,﹣3).
(1)求此一次函数的解析式;
(2)直接写出关于x的不等式kx+b≤2的解集.
11.已知函数y=(2m+1)x+m﹣3,m为常数.
(1)若该函数是正比例函数,求m的值;
(2)若该函数是一次函数,且函数图象经过第一、三、四象限,求m的取值范围.
12.如图,已知一次函数y=kx+b的图象经过点A(0,2),B(4,0),C为直线AB上的动点,正比例函数y=mx的图象经过点C.
(1)求一次函数的表达式;
(2)若点C(1,a),求方程组的解.
13.如图,请根据图象所提供的信息解答下列问题:
(1)交点P的坐标(1,1)是二元一次方程组: 的解;
(2)不等式kx+b<0的解集是 ;
(3)当x 时,kx+b≥mx﹣n;
(4)直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.
14.如图,在平行四边形ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
15.如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF.
16.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,AF=6,平行四边形ABCD周长为40,求平行四边形ABCD的面积.
17.已知:如图,在 ABCD中,点E、F分别在BC、AD上,∠AFB=∠CED.
(1)请判断BF、DE的位置关系,并说明理由;
(2)求证:△ABF≌△CDE.
18.如图,在 ABCD中,点E在AB上,点F在CD上,且AE=CF.
(1)求证:四边形DEBF是平行四边形;
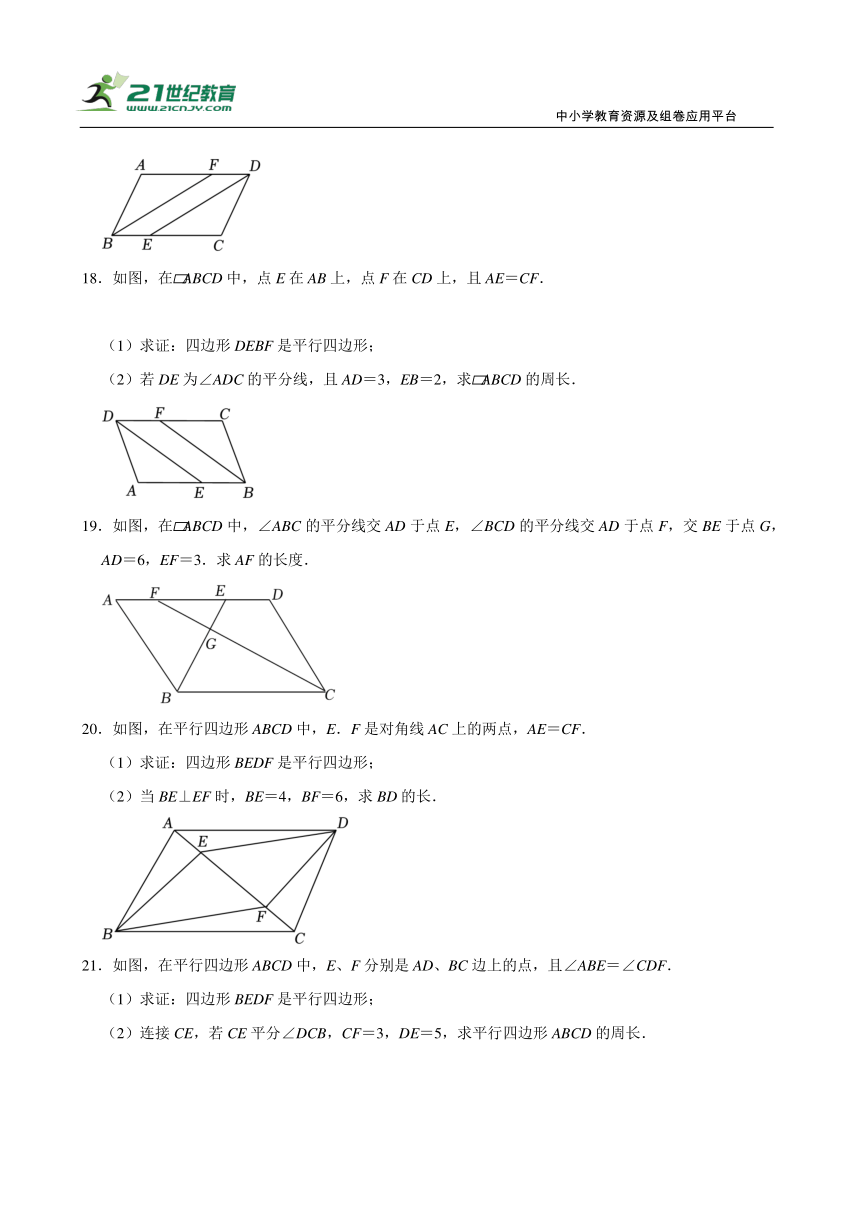
(2)若DE为∠ADC的平分线,且AD=3,EB=2,求 ABCD的周长.
19.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G,AD=6,EF=3.求AF的长度.
20.如图,在平行四边形ABCD中,E.F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)当BE⊥EF时,BE=4,BF=6,求BD的长.
21.如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且∠ABE=∠CDF.
(1)求证:四边形BEDF是平行四边形;
(2)连接CE,若CE平分∠DCB,CF=3,DE=5,求平行四边形ABCD的周长.
22.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,OFOA,OEOC,连接BE,BF,DE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若BE⊥AC,CE=12,DF=8,求BD的长.
23.如图,E,F是 ABCD的对角线AC上两点,DF∥BE.
(1)求证:四边形DEBF为平行四边形;
(2)若AC=8,AB=6,∠CAB=30°,求平行四边形ABCD的面积.
24.如图,在△ABC中,F是AB上一点,连接CF,过点A作AD∥FC,E是AC的中点,连接FE并延长,交AD于点D,连接CD.
(1)求证:四边形AFCD是平行四边形.
(2)若,BF=1,∠DCB=135°,请直接写出FC的长度.
25.如图,在△ABC中,点D在BC上,且DC=AC,CE⊥AD于点E,点F是AB的中点.求证:BD=2EF.
一次函数与平行四边形 专项练习
一.选择题(共1小题)
1.若函数y=(m+1)x|m|﹣5是一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.0
【思路点拔】由一次函数的定义可知|m|=1且m+1≠0,从而可求得m的值.
【解答】解:∵y=(m+1)x|m|﹣5是一次函数,
∴|m|=1且m+1≠0,
解得m=±1且m≠﹣1,
∴m=1.
故选:A.
二.填空题(共8小题)
2.直线y1=ax与直线在同一平面直角坐标系中的图象如图所示,关于x的不等式的解集为 x>﹣2 .
【思路点拔】根据图象,找直线y1在y2下方部分的x的取值范围即可.
【解答】解:由图可知:两条直线的交点横坐标为﹣2,
由知,直线y1在直线y2的下方,
∵当x>﹣2时,直线l1在直线l2的下方,
∴关于x的不等式的解集为x>﹣2.
故答案为:x>﹣2.
3.如图,已知函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),则不等式ax+b≤kx﹣3的解集是 x≤4 .
【思路点拔】直线y=ax+b落在直线y=kx﹣3下方的部分对应的x的取值范围即为所求.
【解答】解:∵函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),
∴不等式ax+b≤kx﹣3的解集是x≤4.
故答案为x≤4.
4.根据图象,可得关于x的不等式kx<﹣x+3的解集是 x<1 .
【思路点拔】先根据函数图象得出交点坐标,根据交点的坐标和图象即可得出答案.
【解答】解:根据图象可知:两函数图象的交点为(1,2),
所以关于x的一元一次不等式kx<﹣x+3的解集为x<1,
故答案为:x<1.
5.如图,一次函数y=kx+b(k≠0)的图象经过点A(a,﹣2),一次函数y=2x的图象过点A,则不等式2x≤kx+b的解集为 x≤﹣1 .
【思路点拔】根据图象可知一次函数y=kx+b,与一次函数y=2x的图象的交点,即可得出不等式2x≤kx+b的解集.
【解答】解:∵一次函数y=2x的图象过点A(a,﹣2),
∴﹣2=2a,
∴a=﹣1,
∴A(﹣1,﹣2),
∵一次函数y=kx+b与一次函数y=2x的图象的交点为A(﹣1,﹣2),
又∵2x≤kx+b,
∴根据图象可得出直线y=2x在直线y=kx+b的下方,
∴2x≤kx+b的解集为x≤﹣1.
故答案为:x≤﹣1.
6.如图,在平面直角坐标系中,直线y=kx+b(k≠0)与x轴交于点(﹣2,0),与y轴交于点(0,1),则不等式kx+b>0的解集为 x>﹣2 .
【思路点拔】从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标.根据直线y=kx+b与x轴交于点(﹣2,0),结合函数图象,即可求出不等式kx+b>0的解集.
【解答】解:∵直线y=kx+b与x轴交于点(﹣2,0),与y轴交于点(0,1),
∴根据函数图象可知,不等式kx+b>0的解集是x>﹣2.
故答案为:x>﹣2.
7.在平面直角坐标系中,一次函数y=ax和y=kx+7的图象如图所示,则关于x的一元一次不等式ax>kx+7的解集是 x>2 .
【思路点拔】根据图象正比例函数在一次函数图象上方对应的x的取值范围即可.
【解答】解:由图可知:一次函数y=ax和y=kx+7的交点处x=2,
∴ax>kx+7的解集是x>2,
故答案为:x>2.
8.如图,点A(﹣1,2)在一次函数y=kx+b(k≠0,且k,b为常数)的图象上,则关于x的不等式kx+b>2的解集是 x<﹣1 .
【思路点拔】由图象可得出答案.
【解答】解:由图象可得:关于x的不等式kx+b>2的解集应是x<﹣1;
故答案为:x<﹣1.
9.如图,已知一次函数y=kx+b的图象经过点A(﹣2,3)和点B(﹣4,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为 ﹣4<x<﹣2 .
【思路点拔】利用函数图象,写出在x轴上方且函数y=kx+b的函数值小于函数y=mx的函数值对应的自变量的范围即可.
【解答】解:当x>﹣4时,y=kx+b>0;
当x<﹣2时,kx+b<mx,
所以不等式组0<kx+b<mx的解集为﹣4<x<﹣2.
故答案为:﹣4<x<﹣2.
三.解答题(共16小题)
10.如图,一次函数y=kx+b(k≠0)的图象过点A(﹣2,2),B(2,﹣3).
(1)求此一次函数的解析式;
(2)直接写出关于x的不等式kx+b≤2的解集.
【思路点拔】(1)将A、B两点代入一次函数,利用待定系数法即可解决问题;
(2)观察图象写出函数值小于等于2的自变量的取值范围即可.
【解答】解:(1)∵一次函数y=kx+b(k≠0)的图象过点A(﹣2,2),B(2,﹣3),
∴,
解得:,
∴一次函数的解析式为:,
故答案为:.
(2)观察图像可知:kx+b≤2时,x≥﹣2,
故答案为:x≥﹣2.
11.已知函数y=(2m+1)x+m﹣3,m为常数.
(1)若该函数是正比例函数,求m的值;
(2)若该函数是一次函数,且函数图象经过第一、三、四象限,求m的取值范围.
【思路点拔】(1)根据y是x的正比例函数列方程,即可得到结论;
(2)根据y是x的一次函数,且图象经过一、三、四象限列不等式组,即可得到结论.
【解答】解:(1)对于y关于x的函数y=(2m+1)x+m﹣3,
∵y是x的正比例函数,
∴m﹣3=0且2m+1≠0,
解得:m=3;
(2)∵y是x的一次函数,且图象经过一、三、四象限,
∴,
解得:,
故m的取值范围为.
12.如图,已知一次函数y=kx+b的图象经过点A(0,2),B(4,0),C为直线AB上的动点,正比例函数y=mx的图象经过点C.
(1)求一次函数的表达式;
(2)若点C(1,a),求方程组的解.
【思路点拔】(1)直接利用待定系数法解答,即可求解;
(2)求出点C的坐标,将方程组整理为,可得方程组的解为一次函数y=kx+b与正比例函数y=mx的交点坐标,即可求解.
【解答】解:(1)∵一次函数图象过点A(0,2),B(4,0),
,解得,
∴一次函数的表达式为:.
(2)将C(1,a)代入得:
,
∴,
将方程组整理为,
∴方程组的解为一次函数y=kx+b与正比例函数y=mx的交点坐标,
∴方程组的解为.
13.如图,请根据图象所提供的信息解答下列问题:
(1)交点P的坐标(1,1)是二元一次方程组: 的解;
(2)不等式kx+b<0的解集是 x>3 ;
(3)当x x≤1 时,kx+b≥mx﹣n;
(4)直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.
【思路点拔】(1)根据函数图象即可求解;
(2)根据函数图象即可求解;
(3)根据函数图象即可求解;
(4)利用待定系数法求出直线l1、l2的解析式,求出点N、M的坐标,再根据计算即可求解.
【解答】解:(1)由图象可得,交点P的坐标(1,1)是一元二次方程组的解,
故答案为:;
(2)由图象可得,不等式kx+b<0的解集是x>3,
故答案为:x>3;
(3)由图象可得,当x≤1时,kx+b≥mx﹣n,
故答案为:x≤1;
(4)把P(1,1),B(3,0)代入y=kx+b得,
,
解得,
∴直线l2的解析式为,
∴,
∴,
同理可得直线l1的解析式为y=2x﹣1,
当y=0时,0=2x﹣1,
∴,
∴,
∴,
∴,
∴四边形OMPN的面积.
14.如图,在平行四边形ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
【思路点拔】可以把要证明相等的线段BE、DF分别放到两个三角形中,即△ABE和△CDF中,寻找它们全等的条件(AAS),得出对应边相等BE=DF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边平行且相等),
∴∠BAE=∠DCF(两直线平行内错角相等),
∵BE⊥AC于E,DF⊥AC于F,
∴∠AEB=∠CFD=90°(垂直定义),
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF(全等三角形的对应边相等).
15.如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF.
【思路点拔】先判断出DE=BF,进而判断出△DOE≌△BOF即可.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODE=∠OBF,
∵AE=CF,
∴DE=BF,且∠DOE=∠BOF,∠ODE=∠OBF,
∴△DOE≌△BOF(AAS),
∴OE=OF
16.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,AF=6,平行四边形ABCD周长为40,求平行四边形ABCD的面积.
【思路点拔】由平行四边形ABCD的周长为40,求得BC+CD=20,由BC AE=CD AF=S四边形ABCD,得4BC=6CD,则BCCD,所以CD+CD=20,求得CD=8,进而求得S四边形ABCD=48,于是得到问题的答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵平行四边形ABCD的周长为40,
∴2BC+2CD=40,
∴BC+CD=20,
∵AE⊥BC于点E,AF⊥CD于点F,且AE=4,AF=6,
∴BC AE=CD AF=S四边形ABCD,
∴4BC=6CD,
∴BCCD,
∴CD+CD=20,
∴CD=8,
∴S四边形ABCD=CD AF=8×6=48,
故答案为:48.
17.已知:如图,在 ABCD中,点E、F分别在BC、AD上,∠AFB=∠CED.
(1)请判断BF、DE的位置关系,并说明理由;
(2)求证:△ABF≌△CDE.
【思路点拔】(1)根据平行四边形性质,结合平行线的判定与性质即可得到BF、DE的位置关系;
(2)由平行四边形性质得到AB=CD,∠A=∠C,再由两个三角形全等的判定定理AAS求证即可得到答案.
【解答】(1)解:BF∥DE,理由如下:
在 ABCD中,AD∥BC,
∴∠AFB=∠CBF,
∵∠AFB=∠CED,
∴∠CBF=∠CED.
∴BF∥DE;
(2)证明:在 ABCD中,AB=CD,∠A=∠C,
在△ABF和△CDE中,
∴△ABF≌△CDE(AAS).
18.如图,在 ABCD中,点E在AB上,点F在CD上,且AE=CF.
(1)求证:四边形DEBF是平行四边形;
(2)若DE为∠ADC的平分线,且AD=3,EB=2,求 ABCD的周长.
【思路点拔】(1)由平行四边形的在得AB=CD,AB∥CD,再证BE=DF,然后由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得AB=CD,AD=BC=3,AB∥CD,再证∠ADE=∠AED,得AE=AD=3,则AB=AE+EB=5,即可解决问题.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴AB﹣AE=CD﹣CF,
即BE=DF,
∴四边形DEBF是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=3,AB∥CD,
∴∠AED=∠CDE,
∵DE为∠ADC的平分线,
∴∠ADE=∠CDE,
∴∠ADE=∠AED,
∴AE=AD=3,
∴AB=AE+EB=3+2=5,
∴ ABCD的周长=2(AB+AD)=2×(5+3)=16.
19.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G,AD=6,EF=3.求AF的长度.
【思路点拔】根据平行四边形的性质可得:AB=CD,AD∥BC,根据平行线性质和角平分线性质求出∠ABE=∠AEB,推出AB=AE,同理求出DF=CD,即可证明AE=DF,再根据线段的和差求解即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理可得:DF=CD,
∴AE=DF,
即AF+EF=DE+EF,
∴AF=DE,
∵AD=6,EF=3,
∴AF+DE=AD﹣EF=3,
∴AF.
20.如图,在平行四边形ABCD中,E.F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)当BE⊥EF时,BE=4,BF=6,求BD的长.
【思路点拔】(1)连接BD交AC于点O,由平行四边形的性质得OA=OC,OB=OD,再证OE=OF,然后由平行四边形的判定即可得出结论;
(2)由勾股定理求得EF的长,得出OE的长,再由勾股定理求出OB的长,即可得出结论.
【解答】(1)证明:如图,连接BD交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形BEDF是平行四边形;
(2)解:∵BE⊥EF,
∴∠BEF=90°,
∴EF2,
由(1)可知,OE=OF,OB=OD,
∴OE=OFEF,
∴OB,
∴BD=2OB=2,
即BD的长为2.
21.如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且∠ABE=∠CDF.
(1)求证:四边形BEDF是平行四边形;
(2)连接CE,若CE平分∠DCB,CF=3,DE=5,求平行四边形ABCD的周长.
【思路点拔】(1)根据平行四边形的性质和全等三角形的判定和性质得出AE=CF,进而利用平行四边形的判定解答即可;
(2)由平行四边形的性质和角平分线的定义得出DE=CD=5,再求出BC=BF+CF=5+3=8,求解即可.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠A=∠DCF,AB=CD,
∵∠ABE=∠CDF,
∴△ABE≌△CDF(ASA),
∴AE=CF,
∴AD﹣AE=BC﹣CF,
即DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形;
(2)∵四边形BEDF是平行四边形,
∴BF=DE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠DEC=∠ECB,
∵CE平分∠DCB,
∴∠DCE=∠ECB,
∴∠DEC=∠DCE,
∴DE=CD=5,
∴BF=DE=5,
∴BC=BF+CF=5+3=8,
∴平行四边形ABCD的周长=2(BC+CD)=2×(8+5)=26.
22.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,OFOA,OEOC,连接BE,BF,DE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若BE⊥AC,CE=12,DF=8,求BD的长.
【思路点拔】(1)由平行四边形的性质得OB=OD,OA=OC,再证OF=OE,然后由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得BE=DF=8,再求出OECE=6,然后由勾股定理得OB=10,即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵OFOA,OEOC,
∴OF=OE,
∴四边形BEDF是平行四边形;
(2)解:由(1)可知,OB=OD,四边形BEDF是平行四边形,
∴BE=DF=8,
∵OEOC,CE=12,
∴OECE=6,
∵BE⊥AC,
∴∠BEO=90°,
∴OB10,
∴BD=2OB=20,
即BD的长为20.
23.如图,E,F是 ABCD的对角线AC上两点,DF∥BE.
(1)求证:四边形DEBF为平行四边形;
(2)若AC=8,AB=6,∠CAB=30°,求平行四边形ABCD的面积.
【思路点拔】(1)由平行四边形的性质得CD∥AB,CD=AB,则∠DCF=∠BAE,由DF∥BE,得∠CFD=∠AEB,即可证明△CFD≌△AEB,得DF=BE,则四边形DEBF是平行四边形;
(2)作CG⊥AB交AB的延长线于点G,因为∠CAB=30°,所以CGAC=4,则S平行四边形ABCD=6×4=24.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∴∠DCF=∠BAE,
∵DF∥BE,
∴∠CFD=∠AEB,
在△CFD和△AEB中,
,
∴△CFD≌△AEB(AAS),
∴DF=BE,
∴四边形DEBF是平行四边形.
(2)解:作CG⊥AB交AB的延长线于点G,则∠G=90°,
∵∠CAB=30°,AC=8,AB=6,
∴CGAC8=4,
∴S平行四边形ABCD=AB CG=6×4=24,
∴平行四边形ABCD的面积是24.
24.如图,在△ABC中,F是AB上一点,连接CF,过点A作AD∥FC,E是AC的中点,连接FE并延长,交AD于点D,连接CD.
(1)求证:四边形AFCD是平行四边形.
(2)若,BF=1,∠DCB=135°,请直接写出FC的长度.
【思路点拔】(1)由E是AC的中点,得到AE=CE,根据平行线的性质得到∠DAE=∠FCE.根据全等三角形的性质得到AD=CF,由平行四边形的判定定理得到四边形AFCD是平行四边形;
(2)根据平行四边形 到现在得到AB∥CD,根据平行线的性质得到∠B+∠DCB=180°,求得∠B=45°,过点F作FH⊥BC于H,根据勾股定理得到结论.
【解答】(1)证明:∵E是AC的中点,
∴AE=CE,
∵AD∥FC,
∴∠DAE=∠FCE.
在△DAE和△FCE 中,
,
∴△DAE≌△FCE(ASA),
∴AD=CF,
∴四边形AFCD是平行四边形;
(2)解:∵四边形AFCD是平行四边形,
∴AB∥CD,
∴∠B+∠DCB=180°,
∵∠DCB=135°,
∴∠B=45°,
过点F作FH⊥BC于H,
∴∠BFH=45°=∠B,
∴BH=FH,
在Rt△BFH中,BF=1,BH2+FH2=BF2,
∴2BH2=1,
∴BH=FH,
∴CH=BC﹣BH=4,
在Rt△CFH中,FC2=FH2+CH2,
∴FC5.
25.如图,在△ABC中,点D在BC上,且DC=AC,CE⊥AD于点E,点F是AB的中点.求证:BD=2EF.
【思路点拔】根据题意可推出点E是AD的中点,结合点F是AB的中点可得EF是△ABD的中位线,据此即可求证.
【解答】证明:∵DC=AC,CE⊥AD,
∴点E是AD的中点.
∵点F是AB的中点.
∴EF是△ABD的中位线,
∴BD=2EF.
一次函数与平行四边形 专项练习
一.选择题(共1小题)
1.若函数y=(m+1)x|m|﹣5是一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.0
二.填空题(共8小题)
2.直线y1=ax与直线在同一平面直角坐标系中的图象如图所示,关于x的不等式的解集为 .
3.如图,已知函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),则不等式ax+b≤kx﹣3的解集是 .
4.根据图象,可得关于x的不等式kx<﹣x+3的解集是 .
5.如图,一次函数y=kx+b(k≠0)的图象经过点A(a,﹣2),一次函数y=2x的图象过点A,则不等式2x≤kx+b的解集为 .
6.如图,在平面直角坐标系中,直线y=kx+b(k≠0)与x轴交于点(﹣2,0),与y轴交于点(0,1),则不等式kx+b>0的解集为 .
7.在平面直角坐标系中,一次函数y=ax和y=kx+7的图象如图所示,则关于x的一元一次不等式ax>kx+7的解集是 .
8.如图,点A(﹣1,2)在一次函数y=kx+b(k≠0,且k,b为常数)的图象上,则关于x的不等式kx+b>2的解集是 .
9.如图,已知一次函数y=kx+b的图象经过点A(﹣2,3)和点B(﹣4,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为 .
三.解答题(共16小题)
10.如图,一次函数y=kx+b(k≠0)的图象过点A(﹣2,2),B(2,﹣3).
(1)求此一次函数的解析式;
(2)直接写出关于x的不等式kx+b≤2的解集.
11.已知函数y=(2m+1)x+m﹣3,m为常数.
(1)若该函数是正比例函数,求m的值;
(2)若该函数是一次函数,且函数图象经过第一、三、四象限,求m的取值范围.
12.如图,已知一次函数y=kx+b的图象经过点A(0,2),B(4,0),C为直线AB上的动点,正比例函数y=mx的图象经过点C.
(1)求一次函数的表达式;
(2)若点C(1,a),求方程组的解.
13.如图,请根据图象所提供的信息解答下列问题:
(1)交点P的坐标(1,1)是二元一次方程组: 的解;
(2)不等式kx+b<0的解集是 ;
(3)当x 时,kx+b≥mx﹣n;
(4)直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.
14.如图,在平行四边形ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
15.如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF.
16.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,AF=6,平行四边形ABCD周长为40,求平行四边形ABCD的面积.
17.已知:如图,在 ABCD中,点E、F分别在BC、AD上,∠AFB=∠CED.
(1)请判断BF、DE的位置关系,并说明理由;
(2)求证:△ABF≌△CDE.
18.如图,在 ABCD中,点E在AB上,点F在CD上,且AE=CF.
(1)求证:四边形DEBF是平行四边形;
(2)若DE为∠ADC的平分线,且AD=3,EB=2,求 ABCD的周长.
19.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G,AD=6,EF=3.求AF的长度.
20.如图,在平行四边形ABCD中,E.F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)当BE⊥EF时,BE=4,BF=6,求BD的长.
21.如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且∠ABE=∠CDF.
(1)求证:四边形BEDF是平行四边形;
(2)连接CE,若CE平分∠DCB,CF=3,DE=5,求平行四边形ABCD的周长.
22.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,OFOA,OEOC,连接BE,BF,DE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若BE⊥AC,CE=12,DF=8,求BD的长.
23.如图,E,F是 ABCD的对角线AC上两点,DF∥BE.
(1)求证:四边形DEBF为平行四边形;
(2)若AC=8,AB=6,∠CAB=30°,求平行四边形ABCD的面积.
24.如图,在△ABC中,F是AB上一点,连接CF,过点A作AD∥FC,E是AC的中点,连接FE并延长,交AD于点D,连接CD.
(1)求证:四边形AFCD是平行四边形.
(2)若,BF=1,∠DCB=135°,请直接写出FC的长度.
25.如图,在△ABC中,点D在BC上,且DC=AC,CE⊥AD于点E,点F是AB的中点.求证:BD=2EF.
一次函数与平行四边形 专项练习
一.选择题(共1小题)
1.若函数y=(m+1)x|m|﹣5是一次函数,则m的值为( )
A.1 B.﹣1 C.±1 D.0
【思路点拔】由一次函数的定义可知|m|=1且m+1≠0,从而可求得m的值.
【解答】解:∵y=(m+1)x|m|﹣5是一次函数,
∴|m|=1且m+1≠0,
解得m=±1且m≠﹣1,
∴m=1.
故选:A.
二.填空题(共8小题)
2.直线y1=ax与直线在同一平面直角坐标系中的图象如图所示,关于x的不等式的解集为 x>﹣2 .
【思路点拔】根据图象,找直线y1在y2下方部分的x的取值范围即可.
【解答】解:由图可知:两条直线的交点横坐标为﹣2,
由知,直线y1在直线y2的下方,
∵当x>﹣2时,直线l1在直线l2的下方,
∴关于x的不等式的解集为x>﹣2.
故答案为:x>﹣2.
3.如图,已知函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),则不等式ax+b≤kx﹣3的解集是 x≤4 .
【思路点拔】直线y=ax+b落在直线y=kx﹣3下方的部分对应的x的取值范围即为所求.
【解答】解:∵函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),
∴不等式ax+b≤kx﹣3的解集是x≤4.
故答案为x≤4.
4.根据图象,可得关于x的不等式kx<﹣x+3的解集是 x<1 .
【思路点拔】先根据函数图象得出交点坐标,根据交点的坐标和图象即可得出答案.
【解答】解:根据图象可知:两函数图象的交点为(1,2),
所以关于x的一元一次不等式kx<﹣x+3的解集为x<1,
故答案为:x<1.
5.如图,一次函数y=kx+b(k≠0)的图象经过点A(a,﹣2),一次函数y=2x的图象过点A,则不等式2x≤kx+b的解集为 x≤﹣1 .
【思路点拔】根据图象可知一次函数y=kx+b,与一次函数y=2x的图象的交点,即可得出不等式2x≤kx+b的解集.
【解答】解:∵一次函数y=2x的图象过点A(a,﹣2),
∴﹣2=2a,
∴a=﹣1,
∴A(﹣1,﹣2),
∵一次函数y=kx+b与一次函数y=2x的图象的交点为A(﹣1,﹣2),
又∵2x≤kx+b,
∴根据图象可得出直线y=2x在直线y=kx+b的下方,
∴2x≤kx+b的解集为x≤﹣1.
故答案为:x≤﹣1.
6.如图,在平面直角坐标系中,直线y=kx+b(k≠0)与x轴交于点(﹣2,0),与y轴交于点(0,1),则不等式kx+b>0的解集为 x>﹣2 .
【思路点拔】从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标.根据直线y=kx+b与x轴交于点(﹣2,0),结合函数图象,即可求出不等式kx+b>0的解集.
【解答】解:∵直线y=kx+b与x轴交于点(﹣2,0),与y轴交于点(0,1),
∴根据函数图象可知,不等式kx+b>0的解集是x>﹣2.
故答案为:x>﹣2.
7.在平面直角坐标系中,一次函数y=ax和y=kx+7的图象如图所示,则关于x的一元一次不等式ax>kx+7的解集是 x>2 .
【思路点拔】根据图象正比例函数在一次函数图象上方对应的x的取值范围即可.
【解答】解:由图可知:一次函数y=ax和y=kx+7的交点处x=2,
∴ax>kx+7的解集是x>2,
故答案为:x>2.
8.如图,点A(﹣1,2)在一次函数y=kx+b(k≠0,且k,b为常数)的图象上,则关于x的不等式kx+b>2的解集是 x<﹣1 .
【思路点拔】由图象可得出答案.
【解答】解:由图象可得:关于x的不等式kx+b>2的解集应是x<﹣1;
故答案为:x<﹣1.
9.如图,已知一次函数y=kx+b的图象经过点A(﹣2,3)和点B(﹣4,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为 ﹣4<x<﹣2 .
【思路点拔】利用函数图象,写出在x轴上方且函数y=kx+b的函数值小于函数y=mx的函数值对应的自变量的范围即可.
【解答】解:当x>﹣4时,y=kx+b>0;
当x<﹣2时,kx+b<mx,
所以不等式组0<kx+b<mx的解集为﹣4<x<﹣2.
故答案为:﹣4<x<﹣2.
三.解答题(共16小题)
10.如图,一次函数y=kx+b(k≠0)的图象过点A(﹣2,2),B(2,﹣3).
(1)求此一次函数的解析式;
(2)直接写出关于x的不等式kx+b≤2的解集.
【思路点拔】(1)将A、B两点代入一次函数,利用待定系数法即可解决问题;
(2)观察图象写出函数值小于等于2的自变量的取值范围即可.
【解答】解:(1)∵一次函数y=kx+b(k≠0)的图象过点A(﹣2,2),B(2,﹣3),
∴,
解得:,
∴一次函数的解析式为:,
故答案为:.
(2)观察图像可知:kx+b≤2时,x≥﹣2,
故答案为:x≥﹣2.
11.已知函数y=(2m+1)x+m﹣3,m为常数.
(1)若该函数是正比例函数,求m的值;
(2)若该函数是一次函数,且函数图象经过第一、三、四象限,求m的取值范围.
【思路点拔】(1)根据y是x的正比例函数列方程,即可得到结论;
(2)根据y是x的一次函数,且图象经过一、三、四象限列不等式组,即可得到结论.
【解答】解:(1)对于y关于x的函数y=(2m+1)x+m﹣3,
∵y是x的正比例函数,
∴m﹣3=0且2m+1≠0,
解得:m=3;
(2)∵y是x的一次函数,且图象经过一、三、四象限,
∴,
解得:,
故m的取值范围为.
12.如图,已知一次函数y=kx+b的图象经过点A(0,2),B(4,0),C为直线AB上的动点,正比例函数y=mx的图象经过点C.
(1)求一次函数的表达式;
(2)若点C(1,a),求方程组的解.
【思路点拔】(1)直接利用待定系数法解答,即可求解;
(2)求出点C的坐标,将方程组整理为,可得方程组的解为一次函数y=kx+b与正比例函数y=mx的交点坐标,即可求解.
【解答】解:(1)∵一次函数图象过点A(0,2),B(4,0),
,解得,
∴一次函数的表达式为:.
(2)将C(1,a)代入得:
,
∴,
将方程组整理为,
∴方程组的解为一次函数y=kx+b与正比例函数y=mx的交点坐标,
∴方程组的解为.
13.如图,请根据图象所提供的信息解答下列问题:
(1)交点P的坐标(1,1)是二元一次方程组: 的解;
(2)不等式kx+b<0的解集是 x>3 ;
(3)当x x≤1 时,kx+b≥mx﹣n;
(4)直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.
【思路点拔】(1)根据函数图象即可求解;
(2)根据函数图象即可求解;
(3)根据函数图象即可求解;
(4)利用待定系数法求出直线l1、l2的解析式,求出点N、M的坐标,再根据计算即可求解.
【解答】解:(1)由图象可得,交点P的坐标(1,1)是一元二次方程组的解,
故答案为:;
(2)由图象可得,不等式kx+b<0的解集是x>3,
故答案为:x>3;
(3)由图象可得,当x≤1时,kx+b≥mx﹣n,
故答案为:x≤1;
(4)把P(1,1),B(3,0)代入y=kx+b得,
,
解得,
∴直线l2的解析式为,
∴,
∴,
同理可得直线l1的解析式为y=2x﹣1,
当y=0时,0=2x﹣1,
∴,
∴,
∴,
∴,
∴四边形OMPN的面积.
14.如图,在平行四边形ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
【思路点拔】可以把要证明相等的线段BE、DF分别放到两个三角形中,即△ABE和△CDF中,寻找它们全等的条件(AAS),得出对应边相等BE=DF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边平行且相等),
∴∠BAE=∠DCF(两直线平行内错角相等),
∵BE⊥AC于E,DF⊥AC于F,
∴∠AEB=∠CFD=90°(垂直定义),
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF(全等三角形的对应边相等).
15.如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF.
【思路点拔】先判断出DE=BF,进而判断出△DOE≌△BOF即可.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODE=∠OBF,
∵AE=CF,
∴DE=BF,且∠DOE=∠BOF,∠ODE=∠OBF,
∴△DOE≌△BOF(AAS),
∴OE=OF
16.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,AF=6,平行四边形ABCD周长为40,求平行四边形ABCD的面积.
【思路点拔】由平行四边形ABCD的周长为40,求得BC+CD=20,由BC AE=CD AF=S四边形ABCD,得4BC=6CD,则BCCD,所以CD+CD=20,求得CD=8,进而求得S四边形ABCD=48,于是得到问题的答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵平行四边形ABCD的周长为40,
∴2BC+2CD=40,
∴BC+CD=20,
∵AE⊥BC于点E,AF⊥CD于点F,且AE=4,AF=6,
∴BC AE=CD AF=S四边形ABCD,
∴4BC=6CD,
∴BCCD,
∴CD+CD=20,
∴CD=8,
∴S四边形ABCD=CD AF=8×6=48,
故答案为:48.
17.已知:如图,在 ABCD中,点E、F分别在BC、AD上,∠AFB=∠CED.
(1)请判断BF、DE的位置关系,并说明理由;
(2)求证:△ABF≌△CDE.
【思路点拔】(1)根据平行四边形性质,结合平行线的判定与性质即可得到BF、DE的位置关系;
(2)由平行四边形性质得到AB=CD,∠A=∠C,再由两个三角形全等的判定定理AAS求证即可得到答案.
【解答】(1)解:BF∥DE,理由如下:
在 ABCD中,AD∥BC,
∴∠AFB=∠CBF,
∵∠AFB=∠CED,
∴∠CBF=∠CED.
∴BF∥DE;
(2)证明:在 ABCD中,AB=CD,∠A=∠C,
在△ABF和△CDE中,
∴△ABF≌△CDE(AAS).
18.如图,在 ABCD中,点E在AB上,点F在CD上,且AE=CF.
(1)求证:四边形DEBF是平行四边形;
(2)若DE为∠ADC的平分线,且AD=3,EB=2,求 ABCD的周长.
【思路点拔】(1)由平行四边形的在得AB=CD,AB∥CD,再证BE=DF,然后由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得AB=CD,AD=BC=3,AB∥CD,再证∠ADE=∠AED,得AE=AD=3,则AB=AE+EB=5,即可解决问题.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴AB﹣AE=CD﹣CF,
即BE=DF,
∴四边形DEBF是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=3,AB∥CD,
∴∠AED=∠CDE,
∵DE为∠ADC的平分线,
∴∠ADE=∠CDE,
∴∠ADE=∠AED,
∴AE=AD=3,
∴AB=AE+EB=3+2=5,
∴ ABCD的周长=2(AB+AD)=2×(5+3)=16.
19.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G,AD=6,EF=3.求AF的长度.
【思路点拔】根据平行四边形的性质可得:AB=CD,AD∥BC,根据平行线性质和角平分线性质求出∠ABE=∠AEB,推出AB=AE,同理求出DF=CD,即可证明AE=DF,再根据线段的和差求解即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理可得:DF=CD,
∴AE=DF,
即AF+EF=DE+EF,
∴AF=DE,
∵AD=6,EF=3,
∴AF+DE=AD﹣EF=3,
∴AF.
20.如图,在平行四边形ABCD中,E.F是对角线AC上的两点,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)当BE⊥EF时,BE=4,BF=6,求BD的长.
【思路点拔】(1)连接BD交AC于点O,由平行四边形的性质得OA=OC,OB=OD,再证OE=OF,然后由平行四边形的判定即可得出结论;
(2)由勾股定理求得EF的长,得出OE的长,再由勾股定理求出OB的长,即可得出结论.
【解答】(1)证明:如图,连接BD交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形BEDF是平行四边形;
(2)解:∵BE⊥EF,
∴∠BEF=90°,
∴EF2,
由(1)可知,OE=OF,OB=OD,
∴OE=OFEF,
∴OB,
∴BD=2OB=2,
即BD的长为2.
21.如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且∠ABE=∠CDF.
(1)求证:四边形BEDF是平行四边形;
(2)连接CE,若CE平分∠DCB,CF=3,DE=5,求平行四边形ABCD的周长.
【思路点拔】(1)根据平行四边形的性质和全等三角形的判定和性质得出AE=CF,进而利用平行四边形的判定解答即可;
(2)由平行四边形的性质和角平分线的定义得出DE=CD=5,再求出BC=BF+CF=5+3=8,求解即可.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠A=∠DCF,AB=CD,
∵∠ABE=∠CDF,
∴△ABE≌△CDF(ASA),
∴AE=CF,
∴AD﹣AE=BC﹣CF,
即DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形;
(2)∵四边形BEDF是平行四边形,
∴BF=DE,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠DEC=∠ECB,
∵CE平分∠DCB,
∴∠DCE=∠ECB,
∴∠DEC=∠DCE,
∴DE=CD=5,
∴BF=DE=5,
∴BC=BF+CF=5+3=8,
∴平行四边形ABCD的周长=2(BC+CD)=2×(8+5)=26.
22.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,OFOA,OEOC,连接BE,BF,DE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若BE⊥AC,CE=12,DF=8,求BD的长.
【思路点拔】(1)由平行四边形的性质得OB=OD,OA=OC,再证OF=OE,然后由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得BE=DF=8,再求出OECE=6,然后由勾股定理得OB=10,即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵OFOA,OEOC,
∴OF=OE,
∴四边形BEDF是平行四边形;
(2)解:由(1)可知,OB=OD,四边形BEDF是平行四边形,
∴BE=DF=8,
∵OEOC,CE=12,
∴OECE=6,
∵BE⊥AC,
∴∠BEO=90°,
∴OB10,
∴BD=2OB=20,
即BD的长为20.
23.如图,E,F是 ABCD的对角线AC上两点,DF∥BE.
(1)求证:四边形DEBF为平行四边形;
(2)若AC=8,AB=6,∠CAB=30°,求平行四边形ABCD的面积.
【思路点拔】(1)由平行四边形的性质得CD∥AB,CD=AB,则∠DCF=∠BAE,由DF∥BE,得∠CFD=∠AEB,即可证明△CFD≌△AEB,得DF=BE,则四边形DEBF是平行四边形;
(2)作CG⊥AB交AB的延长线于点G,因为∠CAB=30°,所以CGAC=4,则S平行四边形ABCD=6×4=24.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∴∠DCF=∠BAE,
∵DF∥BE,
∴∠CFD=∠AEB,
在△CFD和△AEB中,
,
∴△CFD≌△AEB(AAS),
∴DF=BE,
∴四边形DEBF是平行四边形.
(2)解:作CG⊥AB交AB的延长线于点G,则∠G=90°,
∵∠CAB=30°,AC=8,AB=6,
∴CGAC8=4,
∴S平行四边形ABCD=AB CG=6×4=24,
∴平行四边形ABCD的面积是24.
24.如图,在△ABC中,F是AB上一点,连接CF,过点A作AD∥FC,E是AC的中点,连接FE并延长,交AD于点D,连接CD.
(1)求证:四边形AFCD是平行四边形.
(2)若,BF=1,∠DCB=135°,请直接写出FC的长度.
【思路点拔】(1)由E是AC的中点,得到AE=CE,根据平行线的性质得到∠DAE=∠FCE.根据全等三角形的性质得到AD=CF,由平行四边形的判定定理得到四边形AFCD是平行四边形;
(2)根据平行四边形 到现在得到AB∥CD,根据平行线的性质得到∠B+∠DCB=180°,求得∠B=45°,过点F作FH⊥BC于H,根据勾股定理得到结论.
【解答】(1)证明:∵E是AC的中点,
∴AE=CE,
∵AD∥FC,
∴∠DAE=∠FCE.
在△DAE和△FCE 中,
,
∴△DAE≌△FCE(ASA),
∴AD=CF,
∴四边形AFCD是平行四边形;
(2)解:∵四边形AFCD是平行四边形,
∴AB∥CD,
∴∠B+∠DCB=180°,
∵∠DCB=135°,
∴∠B=45°,
过点F作FH⊥BC于H,
∴∠BFH=45°=∠B,
∴BH=FH,
在Rt△BFH中,BF=1,BH2+FH2=BF2,
∴2BH2=1,
∴BH=FH,
∴CH=BC﹣BH=4,
在Rt△CFH中,FC2=FH2+CH2,
∴FC5.
25.如图,在△ABC中,点D在BC上,且DC=AC,CE⊥AD于点E,点F是AB的中点.求证:BD=2EF.
【思路点拔】根据题意可推出点E是AD的中点,结合点F是AB的中点可得EF是△ABD的中位线,据此即可求证.
【解答】证明:∵DC=AC,CE⊥AD,
∴点E是AD的中点.
∵点F是AB的中点.
∴EF是△ABD的中位线,
∴BD=2EF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
