浙教版八上数学第四--五章综合练习(含答案)
文档属性
| 名称 | 浙教版八上数学第四--五章综合练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 122.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览

文档简介
浙教版八上数学第四-五章综合练习
一、选择题
1.下列表述中能确定准确位置的是( )
A.教室从左到右第3列 B.文博演出中心第10排
C.北偏东 D.东经,北纬
2.已知函数是关于的一次函数,则的值为( )
A. B.3 C. D.9
3.点P在第四象限,且到x轴距离为2,到y轴距离为4,则点P坐标为( )
A. B. C. D.
4.一次函数的图象与y轴的交点坐标是( )
A.(4,0) B.(0,4) C.(2,0) D.(0,2)
5.在一次函数的图象上有、两点,则下列说法正确的是( )
A. B. C. D.无法判断
6.某市出租车收费标准如下表:设行驶里程数为,收费为y元,则y与x()之间的关系式为( )
里程数 收费/元
3以下(含3) 8
3以上每增加1 1.8
A. B. C. D.
7.在平面直角坐标系中,点,,,若平分,轴,轴,且,则的值为( )
A.9 B. C. D.
8.两条直线与在同一平面直角坐标系中的图象位置可能是( )
A. B.
C. D.
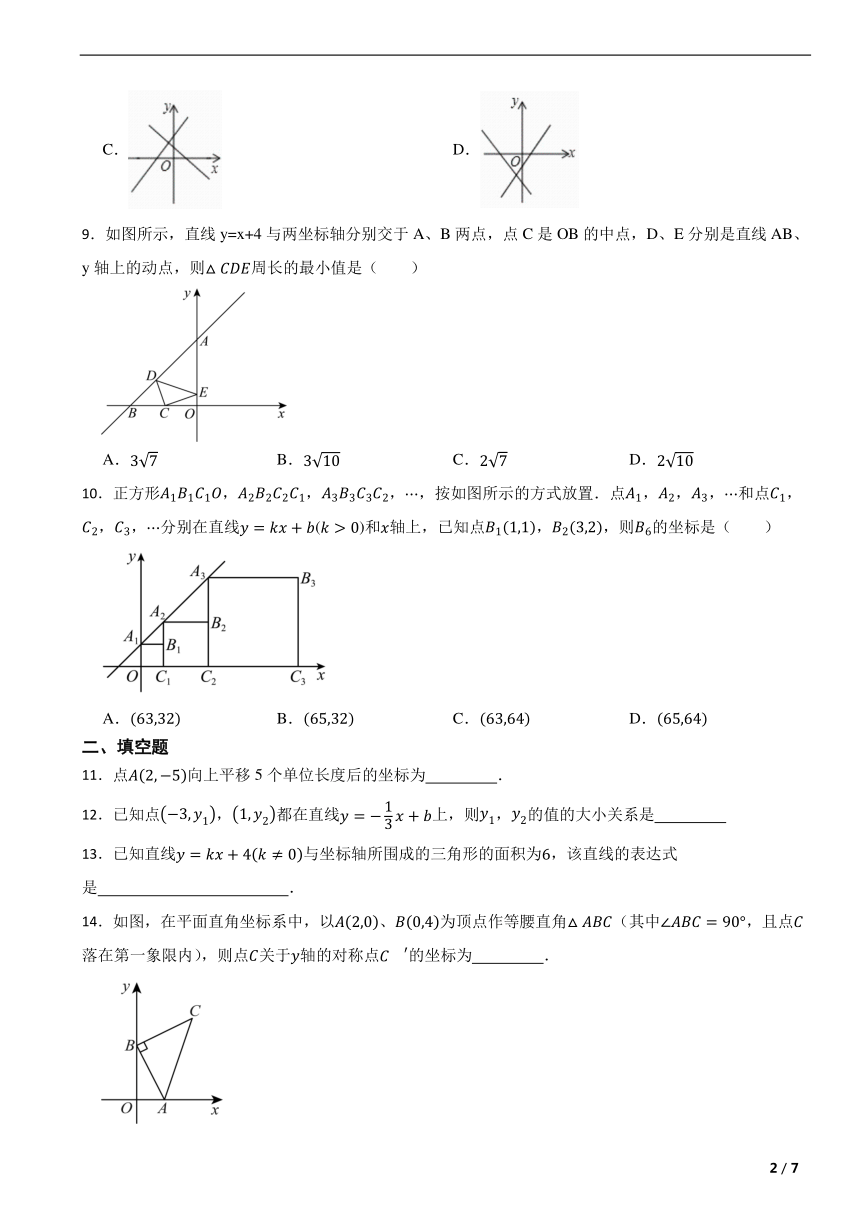
9.如图所示,直线y=x+4与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,则周长的最小值是( )
A. B. C. D.
10.正方形,,,,按如图所示的方式放置.点,,,和点,,,分别在直线()和轴上,已知点,,则的坐标是( )
A. B. C. D.
二、填空题
11.点向上平移5个单位长度后的坐标为 .
12.已知点,都在直线上,则,的值的大小关系是
13.已知直线与坐标轴所围成的三角形的面积为,该直线的表达式是 .
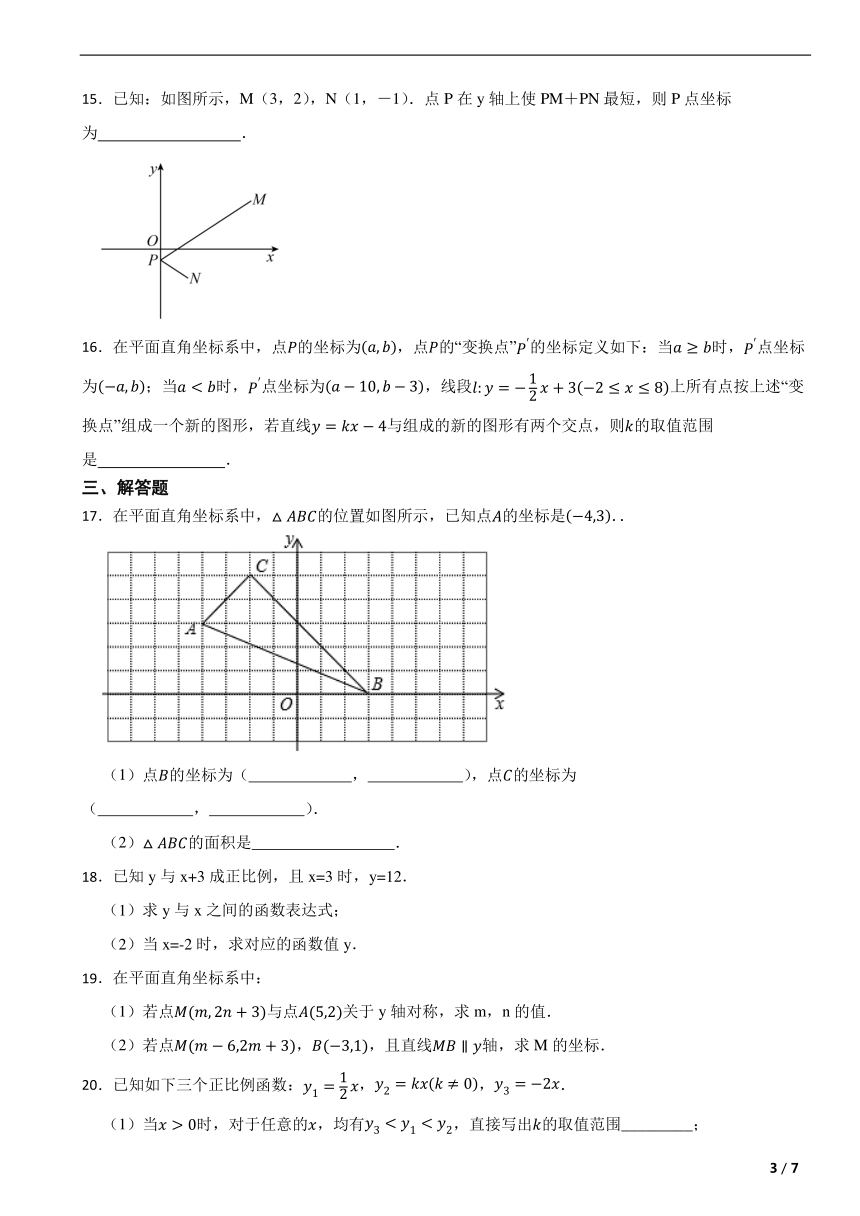
14.如图,在平面直角坐标系中,以、为顶点作等腰直角(其中,且点落在第一象限内),则点关于轴的对称点的坐标为 .
15.已知:如图所示,M(3,2),N(1,-1).点P在y轴上使PM+PN最短,则P点坐标为 .
16.在平面直角坐标系中,点的坐标为,点的“变换点”的坐标定义如下:当时,点坐标为;当时,点坐标为,线段上所有点按上述“变换点”组成一个新的图形,若直线与组成的新的图形有两个交点,则的取值范围是 .
三、解答题
17.在平面直角坐标系中,的位置如图所示,已知点的坐标是..
(1)点的坐标为( , ),点的坐标为( , ).
(2)的面积是 .
18.已知y与x+3成正比例,且x=3时,y=12.
(1)求y与x之间的函数表达式;
(2)当x=-2时,求对应的函数值y.
19.在平面直角坐标系中:
(1)若点与点关于y轴对称,求m,n的值.
(2)若点,,且直线轴,求M的坐标.
20.已知如下三个正比例函数:,,.
(1)当时,对于任意的,均有,直接写出的取值范围_________;
(2)如果直线与顺次交于点、点、点,且,求的值.
21.某市为了节约用水,采用分段收费标准.设居民每月应交水费(元),用水量(立方米).
用水量(立方米) 应交水费(元)
不超过12立方米 每立方米3.5元
超过12立方米 超过的部分每立方米4.5元
(1)某户居民某月用水10立方米,应交水费 元:若用水15立方米,应交水费 元;
(2)求每月应交水费(元)与用水量(立方米)之间的函数关系式;
(3)若某户居民某月交水费78元,则该户居民用水多少立方米
22.在探究一次函数k、b对函数图象和性质的影响时,北师大教材87页探究了“直线与的位置关系如何?你能通过适当的移动将直线变为吗?一般地,直线与又有怎样的关系呢?”根据以上探究结论,解答下列问题:
若直线交坐标轴于A,B两点,将直线向右平移m个单位得到直线.
(1)若时,求:
①直线l1的表达式;
②移动后的直线上到两坐标轴距离相等的点的坐标;
(2)若直线与x轴的交点为P,满足,求m的值.
23.如图,点在直线上,直线上有一点;
(1)求点P和点Q的坐标(其中点Q坐标用含k的代数式表示);
(2)过点P作轴,过点Q作轴,垂足分别是A、B.如果的面积是面积的,请求出k的值;
(3)在(2)的条件下,线段与直线相交于点G,直线上是否存在点D,使?如果存在,请直接写出D的坐标;如果不存在,请说明理由.
参考答案
1.D
2.A
3.C
4.B
5.C
6.D
7.D
8.B
解:当a>0,b>0时
两条直线中:y随x的增大而增大,与y轴交于正半轴,图象经过一,二,三象限
当a>0,b<0时
直线,y随x的增大而增大,与y轴交于负半轴,图象经过一,三,四象限
直线,y随x的增大而减小,与y轴交于正半轴,图象经过一,二,四象限,B选项符合题意
当a<0,b>0时
直线,y随x的增大而减小,与y轴交于正半轴,图象经过一,二,四象限
直线,y随x的增大而增大,与y轴交于负半轴,图象经过一,三,四象限
当a<0,b<0时
两条直线中:y随x的增大而减小,与y轴交于负半轴,图象经过二,三,四象限
9.D
10.A
11.
12.
13.或
14.
15.(0,-)
16.
17.(1)
(2)
18.(1)y=2x+6;
(2)y=2;
19.(1),
(2)
20.(1)
(2)
21.(1)35;55.5
(2)解:由题意可得,
当时,,
当时,,
由上可得,每月应交水费(元)与用水量(立方米)之间的函数关系式是;
(3)解:,
该户居民用水超过12立方米,
设该户居民用水立方米,
则,
解得,
答:该户居民用水20立方米.
22.(1)解: ①设 的表达式为y= kx+b.
∵直线l:y=2x+4交坐标轴于A, B两点,
∴A(-2,0), B(0,4).
将直线向右平移3个单位,则与轴交点(-2,0)变为(1,0), k值不变,
∴直线y=2x+b过(1,0),
∴直线l1的表达式为y= 2x-2.
②到坐标轴距离相等的点有两种情况:
当在y=x上时, 有x=2x--2, 解得x=2,
∴坐标为(2,2).
当在y=-x上时, 有-x=2x-2, 解得
∴坐标为
综上所述:移动后的直线 上到两坐标轴距离相等的点的坐标为(2,2),
(2)解:如图, 设OP =a.
∵ P到点A,点B的距离相等,
∴PA=PB.
在Rt△OAP中,
解得a=3,
∴m=5.
23.(1),
(2)
(3)存在,,
1 / 1
一、选择题
1.下列表述中能确定准确位置的是( )
A.教室从左到右第3列 B.文博演出中心第10排
C.北偏东 D.东经,北纬
2.已知函数是关于的一次函数,则的值为( )
A. B.3 C. D.9
3.点P在第四象限,且到x轴距离为2,到y轴距离为4,则点P坐标为( )
A. B. C. D.
4.一次函数的图象与y轴的交点坐标是( )
A.(4,0) B.(0,4) C.(2,0) D.(0,2)
5.在一次函数的图象上有、两点,则下列说法正确的是( )
A. B. C. D.无法判断
6.某市出租车收费标准如下表:设行驶里程数为,收费为y元,则y与x()之间的关系式为( )
里程数 收费/元
3以下(含3) 8
3以上每增加1 1.8
A. B. C. D.
7.在平面直角坐标系中,点,,,若平分,轴,轴,且,则的值为( )
A.9 B. C. D.
8.两条直线与在同一平面直角坐标系中的图象位置可能是( )
A. B.
C. D.
9.如图所示,直线y=x+4与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,则周长的最小值是( )
A. B. C. D.
10.正方形,,,,按如图所示的方式放置.点,,,和点,,,分别在直线()和轴上,已知点,,则的坐标是( )
A. B. C. D.
二、填空题
11.点向上平移5个单位长度后的坐标为 .
12.已知点,都在直线上,则,的值的大小关系是
13.已知直线与坐标轴所围成的三角形的面积为,该直线的表达式是 .
14.如图,在平面直角坐标系中,以、为顶点作等腰直角(其中,且点落在第一象限内),则点关于轴的对称点的坐标为 .
15.已知:如图所示,M(3,2),N(1,-1).点P在y轴上使PM+PN最短,则P点坐标为 .
16.在平面直角坐标系中,点的坐标为,点的“变换点”的坐标定义如下:当时,点坐标为;当时,点坐标为,线段上所有点按上述“变换点”组成一个新的图形,若直线与组成的新的图形有两个交点,则的取值范围是 .
三、解答题
17.在平面直角坐标系中,的位置如图所示,已知点的坐标是..
(1)点的坐标为( , ),点的坐标为( , ).
(2)的面积是 .
18.已知y与x+3成正比例,且x=3时,y=12.
(1)求y与x之间的函数表达式;
(2)当x=-2时,求对应的函数值y.
19.在平面直角坐标系中:
(1)若点与点关于y轴对称,求m,n的值.
(2)若点,,且直线轴,求M的坐标.
20.已知如下三个正比例函数:,,.
(1)当时,对于任意的,均有,直接写出的取值范围_________;
(2)如果直线与顺次交于点、点、点,且,求的值.
21.某市为了节约用水,采用分段收费标准.设居民每月应交水费(元),用水量(立方米).
用水量(立方米) 应交水费(元)
不超过12立方米 每立方米3.5元
超过12立方米 超过的部分每立方米4.5元
(1)某户居民某月用水10立方米,应交水费 元:若用水15立方米,应交水费 元;
(2)求每月应交水费(元)与用水量(立方米)之间的函数关系式;
(3)若某户居民某月交水费78元,则该户居民用水多少立方米
22.在探究一次函数k、b对函数图象和性质的影响时,北师大教材87页探究了“直线与的位置关系如何?你能通过适当的移动将直线变为吗?一般地,直线与又有怎样的关系呢?”根据以上探究结论,解答下列问题:
若直线交坐标轴于A,B两点,将直线向右平移m个单位得到直线.
(1)若时,求:
①直线l1的表达式;
②移动后的直线上到两坐标轴距离相等的点的坐标;
(2)若直线与x轴的交点为P,满足,求m的值.
23.如图,点在直线上,直线上有一点;
(1)求点P和点Q的坐标(其中点Q坐标用含k的代数式表示);
(2)过点P作轴,过点Q作轴,垂足分别是A、B.如果的面积是面积的,请求出k的值;
(3)在(2)的条件下,线段与直线相交于点G,直线上是否存在点D,使?如果存在,请直接写出D的坐标;如果不存在,请说明理由.
参考答案
1.D
2.A
3.C
4.B
5.C
6.D
7.D
8.B
解:当a>0,b>0时
两条直线中:y随x的增大而增大,与y轴交于正半轴,图象经过一,二,三象限
当a>0,b<0时
直线,y随x的增大而增大,与y轴交于负半轴,图象经过一,三,四象限
直线,y随x的增大而减小,与y轴交于正半轴,图象经过一,二,四象限,B选项符合题意
当a<0,b>0时
直线,y随x的增大而减小,与y轴交于正半轴,图象经过一,二,四象限
直线,y随x的增大而增大,与y轴交于负半轴,图象经过一,三,四象限
当a<0,b<0时
两条直线中:y随x的增大而减小,与y轴交于负半轴,图象经过二,三,四象限
9.D
10.A
11.
12.
13.或
14.
15.(0,-)
16.
17.(1)
(2)
18.(1)y=2x+6;
(2)y=2;
19.(1),
(2)
20.(1)
(2)
21.(1)35;55.5
(2)解:由题意可得,
当时,,
当时,,
由上可得,每月应交水费(元)与用水量(立方米)之间的函数关系式是;
(3)解:,
该户居民用水超过12立方米,
设该户居民用水立方米,
则,
解得,
答:该户居民用水20立方米.
22.(1)解: ①设 的表达式为y= kx+b.
∵直线l:y=2x+4交坐标轴于A, B两点,
∴A(-2,0), B(0,4).
将直线向右平移3个单位,则与轴交点(-2,0)变为(1,0), k值不变,
∴直线y=2x+b过(1,0),
∴直线l1的表达式为y= 2x-2.
②到坐标轴距离相等的点有两种情况:
当在y=x上时, 有x=2x--2, 解得x=2,
∴坐标为(2,2).
当在y=-x上时, 有-x=2x-2, 解得
∴坐标为
综上所述:移动后的直线 上到两坐标轴距离相等的点的坐标为(2,2),
(2)解:如图, 设OP =a.
∵ P到点A,点B的距离相等,
∴PA=PB.
在Rt△OAP中,
解得a=3,
∴m=5.
23.(1),
(2)
(3)存在,,
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
