浙教版七上 第四-五章 综合练习(含答案)
文档属性
| 名称 | 浙教版七上 第四-五章 综合练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 108.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 11:47:34 | ||
图片预览


文档简介
浙教版七上第四-五章综合练习
一、选择题
1.下列说法错误的是( )
A.是二次三项式 B.不是单项式
C.的系数是 D.的次数是6
2.根据等式的性质,下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.,则
3.下列方程中,一元一次方程的是( )
A. B. C. D.
4.用代数式表示“a的3倍与b的平方的差”,正确的是( )
A.(3a-b)2 B.3(a-b)2 C.(a-3b)2 D.3a-b2
5.下列合并同类项正确的是( )
A.3x+2x=5x2 B.3x-2x=1
C.-3x+2x=-x D.-3x-2x=5x
6.若x=-1是方程2x+m-6=0的解,则m的值是( )
A.-4 B.4 C.-8 D.8
7.已知方程2-3(x-1)=2x+10的解和关于x的方程 的解互为相反数,则m的值为 ( )
A.-1 B.1 C.2 D.-2
8.如图,这是一个数值转换机的示意图,若输入x的值为﹣5,则输出的结果为( )
A.﹣10 B.﹣15 C.﹣30 D.﹣40
9.若关于x的一元一次方程 的解为x=-2,则关于y的一元一次方程 的解为( )
A.y=1 B.y=-2 C.y=-3 D.y=-4
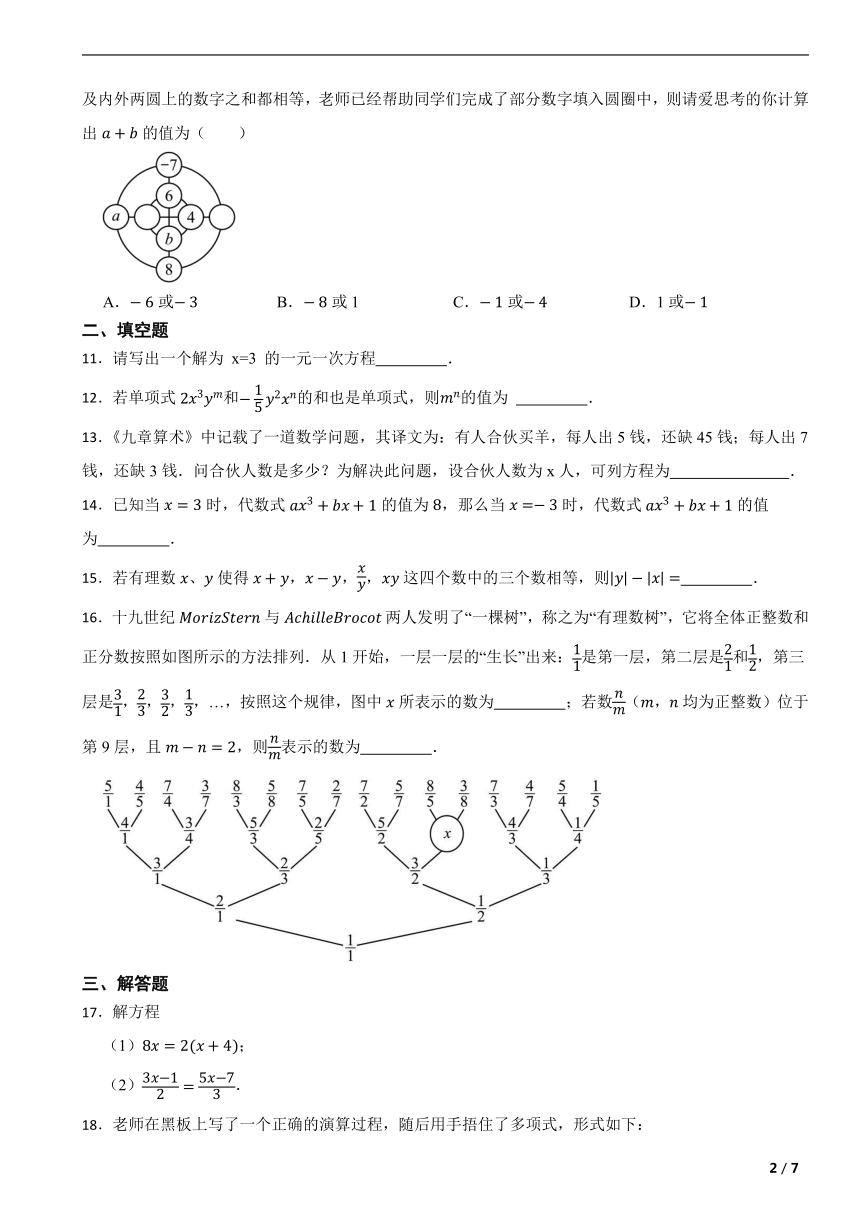
10.如图,老师在探究“幻方”的数学课上稍加创新改成了“幻圆”游戏,让学生们感悟到我国传统数学文化的魅力.一个小组尝试将数字,2,,4,,6,,8这8个数分别填入圆圈内,使横、竖以及内外两圆上的数字之和都相等,老师已经帮助同学们完成了部分数字填入圆圈中,则请爱思考的你计算出的值为( )
A.或 B.或1 C.或 D.1或
二、填空题
11.请写出一个解为 x=3 的一元一次方程 .
12.若单项式和的和也是单项式,则的值为 .
13.《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱.问合伙人数是多少?为解决此问题,设合伙人数为x人,可列方程为 .
14.已知当时,代数式的值为,那么当时,代数式的值为 .
15.若有理数、使得,,,这四个数中的三个数相等,则 .
16.十九世纪与两人发明了“一棵树”,称之为“有理数树”,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,…,按照这个规律,图中所表示的数为 ;若数(,均为正整数)位于第9层,且,则表示的数为 .
三、解答题
17.解方程
(1);
(2).
18.老师在黑板上写了一个正确的演算过程,随后用手捂住了多项式,形式如下:
(1)求所捂住的多项式;
(2)若,求所捂住的多项式的值.
19.若方程的解与方程的解相同,求关于x的方程的解.
20.已知多项式,.
(1)求;
(2)若的值与的值无关,求的值.
21.某茶具生产车间有25名工人生产茶壶和茶杯,1个茶壶和6个茶杯配成一套.已知一名工人一天可以生产3个茶壶或7个茶杯.
(1)要使一天生产的茶壶和茶杯正好配套,应分别安排多少名工人生产茶壶和茶杯?
(2)10月一套茶具的成本比9月提高了20%,9月投入了10万元,10月投入的比9月多5000元,结果生产的茶具比9月少50套,求10月每套茶具的成本是多少元?
22.先阅读下面材料,再解决问题:
在求多项式的值时, 有时可以通过“降次”的方法, 把字母的次数从“高次”降为“低次”.一般有“逐步降次法”和“整体代人法”两种做法.
例如:已知 , 求多项式 的值.
方法一: ,
原式 .
方法二: ,
原式 .
(1) 应用: 已知 , 求多项式 的值(只需用一种方法即可).
(2) 拓展: 已知 , 求多项式 的值(只需用一种方法即可).
23.数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.
初步尝试:
(1)如果点A表示数,将点A向右移动5个单位长度,那么终点B表示的数是_______
(2)如果点A表示数2,将A点先向左移动5个单位长度,再向右移动10个单位长度,那么终点B表示的数是_______
深入研究:
(3)甲、乙两人借助数轴和“剪刀、石头、布”设计了一款“移动游戏”.两人分别在数轴上挑选一个点作为游戏的起点:甲选择的游戏起点A表示的数是,乙选择的游戏起点B表示的数是2;然后两人进行“剪刀、石头、布”,移动规则如下:
“剪刀、石头、布”的结果 两点移动方式
平局 点A向右移动个单位,点B向左移动个单位
甲胜 点A向右移动4个单位,点B向右移动3个单位
乙胜 点A向左移动3个单位,点B向左移动4个单位
设甲、乙两人共进行了m次“剪刀、石头、布”(m为正整数).
①当时,其中平局一次,甲胜两次,点A最终位置表示的数为_______,点B最终位置求示的数为_______,此时两点间的距离为_______.
②若在m次“剪刀、石头、布”中,平局有x次,甲胜有y次,请用含太的式子表示点A和点B最终表示的数;点A和点B会重合吗?如果能重合,请求出m的值;如果点A和点B最终表示的数相距2,请直接写出满足条件的m的值.
参考答案
1 2 3 4 5
C C B D C
6 7 8 9 10
D C C C A
7.
解:2-3(x-1)=2x+10
解得:x= -1
,解得:
∵两个方程的解互为相反数
∴,解得:m=2
9.
解:∵关于x的一元一次方程 的解为x=-2
∴关于y的一元一次方程 的解为y+1=-2
∴y=-2-1=-3
11.2x=6
12.
13.
14.
15.
16.;
17.(1)
(2)
18.(1)
(2)37
19.
20.(1)
(2)
21.(1)安排7名工人生产茶壶,安排18名工人生产茶杯使一天生产的茶壶和茶杯正好配套.
(2)300元
22.(1)解:∵2x2+6x-3=0,
∴x2+3x=,
∴-3x2-9x+4=-3(x2+3x)+4=;
(2)解:∵x2+3x-2=0,
∴x2=2-3x,
∴3x4+12x3+3x2-6x+5
=3(2-3x)2+12x(2-3x)+3(2-3x)-6x+5
=27x2-36x+12-36x2+24x-9x+6-6x+5
=-9x2-27x+23
=-9(2-3x)-27x+23
=-18+27x-27x+23
=5.
23.(1);
(2)7;
(3)①;;;
②点A最终表示的数为,点B最终表示的数为,当A、B重合时,;当点A和点B最终表示的数相距2时,或
解:(1),则点B表示的数为1,
故答案为:;
(2),则B点表示的数是7,
故答案为:7;
(3)①当时,平局一次,甲胜两次,则乙胜一次,
则点A为,点B为,
∴距离为
故答案为;;;;
②在m次游戏中,平局有x次,甲胜有y次,则乙胜次,
∴点A为,
点B为,
当A、B重合时,可得,
解得;
当A、B相距2时,可得,
解得或
1 / 1
一、选择题
1.下列说法错误的是( )
A.是二次三项式 B.不是单项式
C.的系数是 D.的次数是6
2.根据等式的性质,下列变形正确的是( )
A.若,则 B.若,则
C.若,则 D.,则
3.下列方程中,一元一次方程的是( )
A. B. C. D.
4.用代数式表示“a的3倍与b的平方的差”,正确的是( )
A.(3a-b)2 B.3(a-b)2 C.(a-3b)2 D.3a-b2
5.下列合并同类项正确的是( )
A.3x+2x=5x2 B.3x-2x=1
C.-3x+2x=-x D.-3x-2x=5x
6.若x=-1是方程2x+m-6=0的解,则m的值是( )
A.-4 B.4 C.-8 D.8
7.已知方程2-3(x-1)=2x+10的解和关于x的方程 的解互为相反数,则m的值为 ( )
A.-1 B.1 C.2 D.-2
8.如图,这是一个数值转换机的示意图,若输入x的值为﹣5,则输出的结果为( )
A.﹣10 B.﹣15 C.﹣30 D.﹣40
9.若关于x的一元一次方程 的解为x=-2,则关于y的一元一次方程 的解为( )
A.y=1 B.y=-2 C.y=-3 D.y=-4
10.如图,老师在探究“幻方”的数学课上稍加创新改成了“幻圆”游戏,让学生们感悟到我国传统数学文化的魅力.一个小组尝试将数字,2,,4,,6,,8这8个数分别填入圆圈内,使横、竖以及内外两圆上的数字之和都相等,老师已经帮助同学们完成了部分数字填入圆圈中,则请爱思考的你计算出的值为( )
A.或 B.或1 C.或 D.1或
二、填空题
11.请写出一个解为 x=3 的一元一次方程 .
12.若单项式和的和也是单项式,则的值为 .
13.《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱.问合伙人数是多少?为解决此问题,设合伙人数为x人,可列方程为 .
14.已知当时,代数式的值为,那么当时,代数式的值为 .
15.若有理数、使得,,,这四个数中的三个数相等,则 .
16.十九世纪与两人发明了“一棵树”,称之为“有理数树”,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,…,按照这个规律,图中所表示的数为 ;若数(,均为正整数)位于第9层,且,则表示的数为 .
三、解答题
17.解方程
(1);
(2).
18.老师在黑板上写了一个正确的演算过程,随后用手捂住了多项式,形式如下:
(1)求所捂住的多项式;
(2)若,求所捂住的多项式的值.
19.若方程的解与方程的解相同,求关于x的方程的解.
20.已知多项式,.
(1)求;
(2)若的值与的值无关,求的值.
21.某茶具生产车间有25名工人生产茶壶和茶杯,1个茶壶和6个茶杯配成一套.已知一名工人一天可以生产3个茶壶或7个茶杯.
(1)要使一天生产的茶壶和茶杯正好配套,应分别安排多少名工人生产茶壶和茶杯?
(2)10月一套茶具的成本比9月提高了20%,9月投入了10万元,10月投入的比9月多5000元,结果生产的茶具比9月少50套,求10月每套茶具的成本是多少元?
22.先阅读下面材料,再解决问题:
在求多项式的值时, 有时可以通过“降次”的方法, 把字母的次数从“高次”降为“低次”.一般有“逐步降次法”和“整体代人法”两种做法.
例如:已知 , 求多项式 的值.
方法一: ,
原式 .
方法二: ,
原式 .
(1) 应用: 已知 , 求多项式 的值(只需用一种方法即可).
(2) 拓展: 已知 , 求多项式 的值(只需用一种方法即可).
23.数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.
初步尝试:
(1)如果点A表示数,将点A向右移动5个单位长度,那么终点B表示的数是_______
(2)如果点A表示数2,将A点先向左移动5个单位长度,再向右移动10个单位长度,那么终点B表示的数是_______
深入研究:
(3)甲、乙两人借助数轴和“剪刀、石头、布”设计了一款“移动游戏”.两人分别在数轴上挑选一个点作为游戏的起点:甲选择的游戏起点A表示的数是,乙选择的游戏起点B表示的数是2;然后两人进行“剪刀、石头、布”,移动规则如下:
“剪刀、石头、布”的结果 两点移动方式
平局 点A向右移动个单位,点B向左移动个单位
甲胜 点A向右移动4个单位,点B向右移动3个单位
乙胜 点A向左移动3个单位,点B向左移动4个单位
设甲、乙两人共进行了m次“剪刀、石头、布”(m为正整数).
①当时,其中平局一次,甲胜两次,点A最终位置表示的数为_______,点B最终位置求示的数为_______,此时两点间的距离为_______.
②若在m次“剪刀、石头、布”中,平局有x次,甲胜有y次,请用含太的式子表示点A和点B最终表示的数;点A和点B会重合吗?如果能重合,请求出m的值;如果点A和点B最终表示的数相距2,请直接写出满足条件的m的值.
参考答案
1 2 3 4 5
C C B D C
6 7 8 9 10
D C C C A
7.
解:2-3(x-1)=2x+10
解得:x= -1
,解得:
∵两个方程的解互为相反数
∴,解得:m=2
9.
解:∵关于x的一元一次方程 的解为x=-2
∴关于y的一元一次方程 的解为y+1=-2
∴y=-2-1=-3
11.2x=6
12.
13.
14.
15.
16.;
17.(1)
(2)
18.(1)
(2)37
19.
20.(1)
(2)
21.(1)安排7名工人生产茶壶,安排18名工人生产茶杯使一天生产的茶壶和茶杯正好配套.
(2)300元
22.(1)解:∵2x2+6x-3=0,
∴x2+3x=,
∴-3x2-9x+4=-3(x2+3x)+4=;
(2)解:∵x2+3x-2=0,
∴x2=2-3x,
∴3x4+12x3+3x2-6x+5
=3(2-3x)2+12x(2-3x)+3(2-3x)-6x+5
=27x2-36x+12-36x2+24x-9x+6-6x+5
=-9x2-27x+23
=-9(2-3x)-27x+23
=-18+27x-27x+23
=5.
23.(1);
(2)7;
(3)①;;;
②点A最终表示的数为,点B最终表示的数为,当A、B重合时,;当点A和点B最终表示的数相距2时,或
解:(1),则点B表示的数为1,
故答案为:;
(2),则B点表示的数是7,
故答案为:7;
(3)①当时,平局一次,甲胜两次,则乙胜一次,
则点A为,点B为,
∴距离为
故答案为;;;;
②在m次游戏中,平局有x次,甲胜有y次,则乙胜次,
∴点A为,
点B为,
当A、B重合时,可得,
解得;
当A、B相距2时,可得,
解得或
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
