浙教版(2024)数学八上 第五章 一次函数 提高练习(含答案)
文档属性
| 名称 | 浙教版(2024)数学八上 第五章 一次函数 提高练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 14:46:05 | ||
图片预览



文档简介
浙教版八上第五章一次函数提高练习
一、选择题
1.下列曲线(图象),y不是x的函数是( )
A. B.
C. D.
2.以下函数中是的一次函数的是( )
①;②;③;④;
A.个 B.个 C.个 D.个
3.在一次函数中,一次项系数k和常数项b的值分别是( ).
A. B. C. D.
4.已知正比例函数,那么它的图象经过( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
5.已知函数,若y随x的增大而减小,则k的取值范围是( )
A. B. C. D.
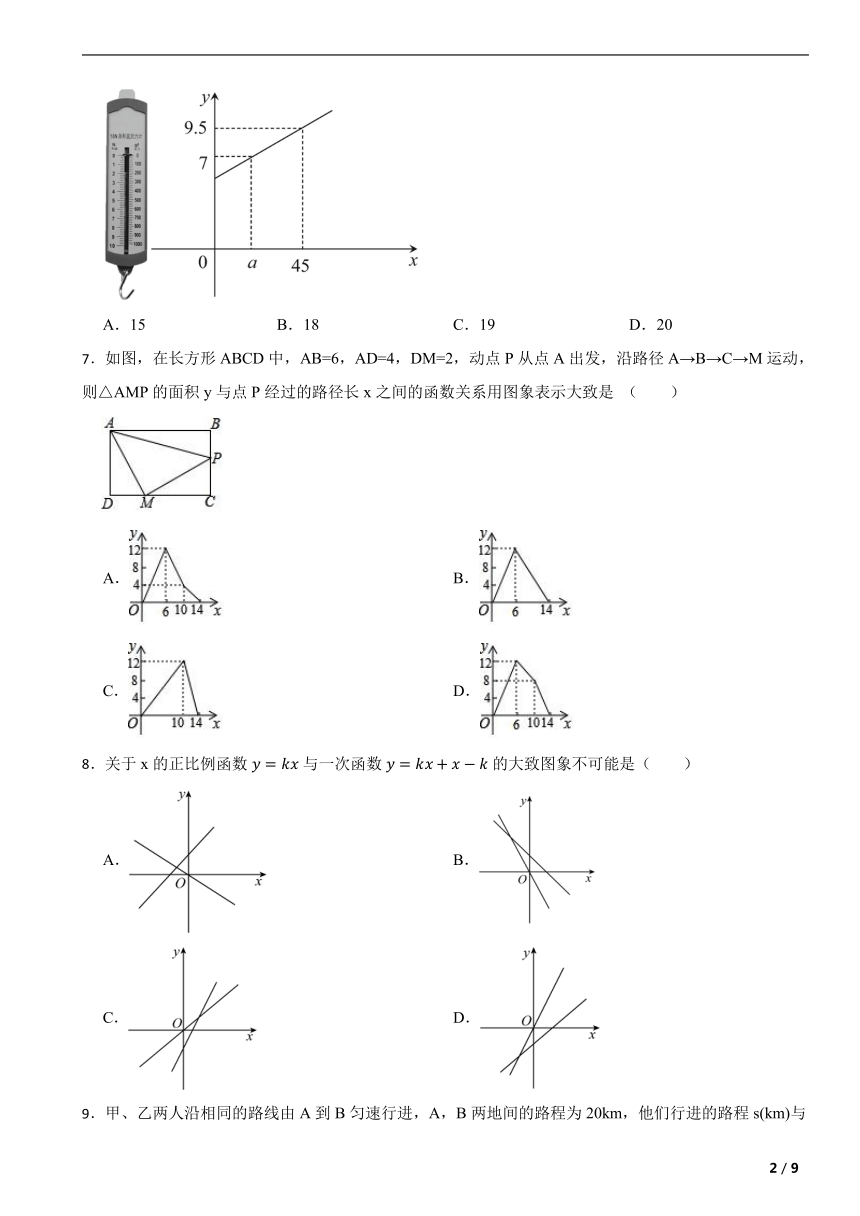
6.如图,一个条形测力计不挂重物时长5cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所测力的大小x(单位:N)的函数图象如图所示,则图中a的值是( )
A.15 B.18 C.19 D.20
7.如图,在长方形ABCD中,AB=6,AD=4,DM=2,动点P从点A出发,沿路径A→B→C→M运动,则△AMP的面积y与点P经过的路径长x之间的函数关系用图象表示大致是 ( )
A. B.
C. D.
8.关于x的正比例函数与一次函数的大致图象不可能是( )
A. B.
C. D.
9.甲、乙两人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km,他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图象的信息,下列说法正确的是( ).
A.甲的速度是4km/h B.乙的速度是10km/h
C.乙比甲早出发1h D.到B地甲比乙晚2h
10.如图所示,已知点C(2,0),直线与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,当的周长取最小值时,点D的坐标为( )
A.(2,1) B.(3,2) C.(,2) D.(,)
二、填空题
11.当m= 时,是一次函数.
12.直线先向左平移2个单位,再向下平移3个单位后得到的新的函数图象的解析式为 .
13.已知直线与坐标轴所围成的三角形的面积为,该直线的表达式是 .
14.如图,大拇指与小拇指尽量张开时,两指尖的距离称为“指距”.研究表明,一般情况下人的身高与指距满足一次函数,若人的身高为时,指距为;当人的身高为时,指距为.篮球运动员姚明的身高为,则据此估计他的指距是 cm.(结果精确到)
15.已知函数y=(k﹣2)x﹣2k+7与,当满足﹣6≤x≤1时,两个函数的图象存在2个公共点,则k满足的条件是 .
16.在平面直角坐标系中,已知点,,.给出如下定义:若点先向上平移个单位(若,即向下平移个单位),再向右平移3个单位后的对应点Q在的内部或边上,则称点P为的“平移关联点”.若直线上的一点P是的“平移关联点”,且是等腰三角形,则点P的坐标为 .
三、解答题
17.已知一次函数(为常数).
(1)若,则这个函数图象不经过第 象限;
(2)若这个函数的图象经过原点,求的值.
18.已知,且是关于的正比例函数.
(1)求与的函数关系式;
(2)若,求函数的最小值.
19.为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
(1)观察图象可知:
(2)直接写出y1、y2与x之间的函数关系式;
(3)某旅行社导游于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A、B两个团队合计50人,求A、B两个团队各有多少人
20.阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线 :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
21.如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,C,经过点C的另一直线与x轴交于点.
(1)求直线的解析式;
(2)若点G是直线上一动点,过点G作x轴的垂线交x轴于点M ,与直线交于点H,且满足,求点G的横坐标;
(3)若点G 是线段BC上一动点,点N在x轴上,且满足,直接写出点G 和点N的坐标.
四、综合题
22.浦江“包子计划”开展的如火如荼,众多居民希望通过卖包子增加收益.根据提供的材料解决问题.
项目 内容
材料一 “沁园包子”店铺开张,经营早餐销售,有菜包、肉包、豆浆等类型早餐,客户可自行搭配.菜包2元/个,豆浆2元/碗,肉包的总金额y(单位:元)随购买个数x(单位:个)之间的关系如图所示,坐标,均经过该分段函数.
材料二 经过试销,“沁园包子”店铺推出套餐A和套餐B,如下: 套餐A:2菜包+1肉包+1豆浆,6元 套餐B:1菜包+1肉包+2豆浆,7元 现在某顾客有资金30元,想购买任意种类包子6个,豆浆2碗.
材料三 为了吸引顾客,扩大市场,“沁园包子”店铺决定开办线上外卖(运费在3km以内4元,超过3km后每1km收费1元),并对包子和豆浆进行优惠,具体方案如下: 方案一:全场九折(不包括运费) 方案二:①每买5个肉包赠送2个菜包 ②每买3个菜包赠送1碗豆浆 方案三:每购买材料二中的套餐任意2份,赠送肉包2个
任务一 求购买肉包的总价y(单位:元)与购买肉包个数x(单位:个)之间的函数关系式,并写明自变量的取值范围.
任务二 在材料二中,若该顾客想要在一定资金内买到心仪的早餐,求他最多能买肉包的个数、菜包的个数以及豆浆的碗数.
任务三 家住距离早餐店14km的某客户想要在“沁园包子”店铺购买早餐,该客户用预算100元的资金购买早餐,计划购买肉包不少于20个,菜包不多于20个,用买包子剩下的钱买豆浆.若该客户想用材料三中的一种方案购买早餐,在买包子的钱最少的前提下,求他所能买的最多的豆浆碗数,并列举此时该客户的购买方案.
参考答案
1.D
2.C
3.B
4.C
5.A
6.D
7.D
】根据题意
当P在AB上时,
高是4,底由0增加到6,面积从0增加到
当P在BC上时,
即
当P在CM上时, ,
根据解析式找图象,D符合
8.D
9.D
解:观察图象可得:
甲的速度为:20÷4=5(km/h),乙的速度为:20÷1=20(km/h),
故选项AB错误;
从图象可以看出乙晚1小时出发,提前4-2=2(小时)到达.
故选项C错误,选项D正确.
10.D
11.3或0
12.
13.或
14.27.3
解:把x=20,y=160和x=21,y=169代入y=kx+b,
则,
解得:,
∴y=9x 20,
当y=226时,9x 20=226,
解得:x=27≈27.3,
∴姚明的指距约为27.3cm,
15.2≤k<
16.或
17.(1)四
(2)
18.(1)
(2)
19.(1)解:由y1可得:当x=10时,元
未打折之前购票款为:50×10=500元
∴,即a=6
由y2可得:x=10时,y2=500元,未打折,即m=10
当x=20时,y2=900元,超出10人的购票款为:900-500=400元
∴,即b=8
综上所述,a=6,b=8,m=10
(2)y1=30x,
(3)解:设A团有n人,则B团有(50-n)人
当0≤n≤10时
50n+30(50-n)=1900,解得:n=20,不符合题意
当n>10时,
40n+100+30(50-n)=1900,解得:n=30,
则A团有30人,B团有50-30=20人
20.(1)解:设直线l的函数表达式为y=k x+b.
∵直线l与直线y=—2x—1平行,∴k=—2.
∵直线l过点(1,4),∴—2+b=4,∴b=6.
∴直线l的函数表达式为y=—2x+6,直线的图象如图:
(2)解:∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,6)、(3,0).
∵l∥ ,∴直线 为y=—2x+t.
∴C点的坐标为( ,0).
∵t>0,
∴ >0.
∴C点在x轴的正半轴上.
当C点在B点的左侧时, ;
当C点在B点的右侧时, .
∴△ 的面积 关于的函数表达式为
21.(1)直线的解析式为
(2)点G的横坐标为或
(3)
22.任务一:(且为整数),(且为整数);任务二:他最多能买肉包的5个数、此时菜包1个数,豆浆2碗.任务三:在买包子的钱最少的前提下,顾客所能买的最多28豆浆碗,此时按方案一购买20个肉包,0个菜包,碗豆浆即可.
1 / 1
一、选择题
1.下列曲线(图象),y不是x的函数是( )
A. B.
C. D.
2.以下函数中是的一次函数的是( )
①;②;③;④;
A.个 B.个 C.个 D.个
3.在一次函数中,一次项系数k和常数项b的值分别是( ).
A. B. C. D.
4.已知正比例函数,那么它的图象经过( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
5.已知函数,若y随x的增大而减小,则k的取值范围是( )
A. B. C. D.
6.如图,一个条形测力计不挂重物时长5cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所测力的大小x(单位:N)的函数图象如图所示,则图中a的值是( )
A.15 B.18 C.19 D.20
7.如图,在长方形ABCD中,AB=6,AD=4,DM=2,动点P从点A出发,沿路径A→B→C→M运动,则△AMP的面积y与点P经过的路径长x之间的函数关系用图象表示大致是 ( )
A. B.
C. D.
8.关于x的正比例函数与一次函数的大致图象不可能是( )
A. B.
C. D.
9.甲、乙两人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km,他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图象的信息,下列说法正确的是( ).
A.甲的速度是4km/h B.乙的速度是10km/h
C.乙比甲早出发1h D.到B地甲比乙晚2h
10.如图所示,已知点C(2,0),直线与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,当的周长取最小值时,点D的坐标为( )
A.(2,1) B.(3,2) C.(,2) D.(,)
二、填空题
11.当m= 时,是一次函数.
12.直线先向左平移2个单位,再向下平移3个单位后得到的新的函数图象的解析式为 .
13.已知直线与坐标轴所围成的三角形的面积为,该直线的表达式是 .
14.如图,大拇指与小拇指尽量张开时,两指尖的距离称为“指距”.研究表明,一般情况下人的身高与指距满足一次函数,若人的身高为时,指距为;当人的身高为时,指距为.篮球运动员姚明的身高为,则据此估计他的指距是 cm.(结果精确到)
15.已知函数y=(k﹣2)x﹣2k+7与,当满足﹣6≤x≤1时,两个函数的图象存在2个公共点,则k满足的条件是 .
16.在平面直角坐标系中,已知点,,.给出如下定义:若点先向上平移个单位(若,即向下平移个单位),再向右平移3个单位后的对应点Q在的内部或边上,则称点P为的“平移关联点”.若直线上的一点P是的“平移关联点”,且是等腰三角形,则点P的坐标为 .
三、解答题
17.已知一次函数(为常数).
(1)若,则这个函数图象不经过第 象限;
(2)若这个函数的图象经过原点,求的值.
18.已知,且是关于的正比例函数.
(1)求与的函数关系式;
(2)若,求函数的最小值.
19.为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
(1)观察图象可知:
(2)直接写出y1、y2与x之间的函数关系式;
(3)某旅行社导游于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A、B两个团队合计50人,求A、B两个团队各有多少人
20.阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线 :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
21.如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,C,经过点C的另一直线与x轴交于点.
(1)求直线的解析式;
(2)若点G是直线上一动点,过点G作x轴的垂线交x轴于点M ,与直线交于点H,且满足,求点G的横坐标;
(3)若点G 是线段BC上一动点,点N在x轴上,且满足,直接写出点G 和点N的坐标.
四、综合题
22.浦江“包子计划”开展的如火如荼,众多居民希望通过卖包子增加收益.根据提供的材料解决问题.
项目 内容
材料一 “沁园包子”店铺开张,经营早餐销售,有菜包、肉包、豆浆等类型早餐,客户可自行搭配.菜包2元/个,豆浆2元/碗,肉包的总金额y(单位:元)随购买个数x(单位:个)之间的关系如图所示,坐标,均经过该分段函数.
材料二 经过试销,“沁园包子”店铺推出套餐A和套餐B,如下: 套餐A:2菜包+1肉包+1豆浆,6元 套餐B:1菜包+1肉包+2豆浆,7元 现在某顾客有资金30元,想购买任意种类包子6个,豆浆2碗.
材料三 为了吸引顾客,扩大市场,“沁园包子”店铺决定开办线上外卖(运费在3km以内4元,超过3km后每1km收费1元),并对包子和豆浆进行优惠,具体方案如下: 方案一:全场九折(不包括运费) 方案二:①每买5个肉包赠送2个菜包 ②每买3个菜包赠送1碗豆浆 方案三:每购买材料二中的套餐任意2份,赠送肉包2个
任务一 求购买肉包的总价y(单位:元)与购买肉包个数x(单位:个)之间的函数关系式,并写明自变量的取值范围.
任务二 在材料二中,若该顾客想要在一定资金内买到心仪的早餐,求他最多能买肉包的个数、菜包的个数以及豆浆的碗数.
任务三 家住距离早餐店14km的某客户想要在“沁园包子”店铺购买早餐,该客户用预算100元的资金购买早餐,计划购买肉包不少于20个,菜包不多于20个,用买包子剩下的钱买豆浆.若该客户想用材料三中的一种方案购买早餐,在买包子的钱最少的前提下,求他所能买的最多的豆浆碗数,并列举此时该客户的购买方案.
参考答案
1.D
2.C
3.B
4.C
5.A
6.D
7.D
】根据题意
当P在AB上时,
高是4,底由0增加到6,面积从0增加到
当P在BC上时,
即
当P在CM上时, ,
根据解析式找图象,D符合
8.D
9.D
解:观察图象可得:
甲的速度为:20÷4=5(km/h),乙的速度为:20÷1=20(km/h),
故选项AB错误;
从图象可以看出乙晚1小时出发,提前4-2=2(小时)到达.
故选项C错误,选项D正确.
10.D
11.3或0
12.
13.或
14.27.3
解:把x=20,y=160和x=21,y=169代入y=kx+b,
则,
解得:,
∴y=9x 20,
当y=226时,9x 20=226,
解得:x=27≈27.3,
∴姚明的指距约为27.3cm,
15.2≤k<
16.或
17.(1)四
(2)
18.(1)
(2)
19.(1)解:由y1可得:当x=10时,元
未打折之前购票款为:50×10=500元
∴,即a=6
由y2可得:x=10时,y2=500元,未打折,即m=10
当x=20时,y2=900元,超出10人的购票款为:900-500=400元
∴,即b=8
综上所述,a=6,b=8,m=10
(2)y1=30x,
(3)解:设A团有n人,则B团有(50-n)人
当0≤n≤10时
50n+30(50-n)=1900,解得:n=20,不符合题意
当n>10时,
40n+100+30(50-n)=1900,解得:n=30,
则A团有30人,B团有50-30=20人
20.(1)解:设直线l的函数表达式为y=k x+b.
∵直线l与直线y=—2x—1平行,∴k=—2.
∵直线l过点(1,4),∴—2+b=4,∴b=6.
∴直线l的函数表达式为y=—2x+6,直线的图象如图:
(2)解:∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,6)、(3,0).
∵l∥ ,∴直线 为y=—2x+t.
∴C点的坐标为( ,0).
∵t>0,
∴ >0.
∴C点在x轴的正半轴上.
当C点在B点的左侧时, ;
当C点在B点的右侧时, .
∴△ 的面积 关于的函数表达式为
21.(1)直线的解析式为
(2)点G的横坐标为或
(3)
22.任务一:(且为整数),(且为整数);任务二:他最多能买肉包的5个数、此时菜包1个数,豆浆2碗.任务三:在买包子的钱最少的前提下,顾客所能买的最多28豆浆碗,此时按方案一购买20个肉包,0个菜包,碗豆浆即可.
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
