第一章 二次函数 复习(含答案)2024--2025学年浙教版九年级数学上册
文档属性
| 名称 | 第一章 二次函数 复习(含答案)2024--2025学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 220.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 15:45:57 | ||
图片预览




文档简介
第一章二次函复习2024--2025学年浙教版九年级数学上册
一、选择题
1.下列函数中,属于二次函数的是 ( )
A. B. C. D.
2.在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向上平移1个单位长度,所得函数的解析式为( )
A. B. C. D.
3.抛物线的顶点坐标( )
A. B. C. D.
4.关于二次函数的图象,下列说法正确的是( )
A.它可由向右平移一个单位得到
B.开口向下
C.顶点坐标是
D.与轴有两个交点
5.函数的图象与轴的交点的情况是( )
A.有两个交点 B.有一个交点 C.没有交点 D.无法判断
6.如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为( )
A.2 B.8 C.10 D.
7.二次函数y=ax2+bx+c的图象如图所示,则点(a,b+c)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知点(2,y1),(1,y2),(-1,y3)在抛物线y=-x2+2x+m上,则( )
A. B. C. D.
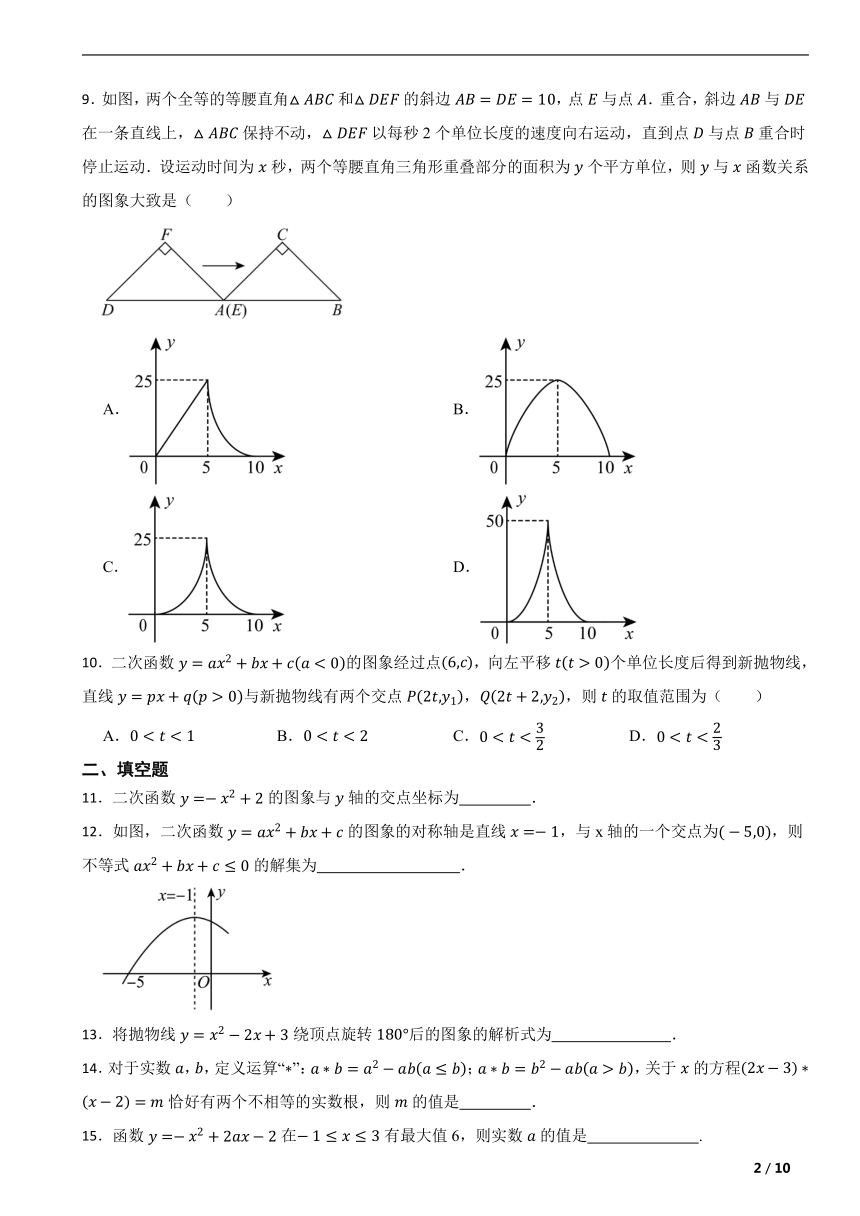
9.如图,两个全等的等腰直角和的斜边,点与点.重合,斜边与在一条直线上,保持不动,以每秒2个单位长度的速度向右运动,直到点与点重合时停止运动.设运动时间为秒,两个等腰直角三角形重叠部分的面积为个平方单位,则与函数关系的图象大致是( )
A. B.
C. D.
10.二次函数的图象经过点,向左平移个单位长度后得到新抛物线,直线与新抛物线有两个交点,,则的取值范围为( )
A. B. C. D.
二、填空题
11.二次函数的图象与轴的交点坐标为 .
12.如图,二次函数的图象的对称轴是直线,与x轴的一个交点为,则不等式的解集为 .
13.将抛物线绕顶点旋转后的图象的解析式为 .
14.对于实数,,定义运算“”:;,关于的方程恰好有两个不相等的实数根,则的值是 .
15.函数在有最大值6,则实数的值是 .
16.如图所示,抛物线与轴交于点和点,与轴交于点,且,点、是直线上的两个动点,且(点在点的上方),则四边形的最小值是 .
三、解答题
17.在平面直角坐标系中,抛物线经过和两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴和顶点坐标.
18.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点,与y轴交于点C,直线经过B、C两点,已知,.
(1)求直线和抛物线的解析式;
(2)求抛物线的顶点D的坐标;
(3)求的面积.
19.已知二次函数(如图).
(1)用配方法将化成的形式;
(2)设抛物线与x轴的一个交点为A(非原点),顶点为B,则A点坐标为 ,B点坐标为 ;
(3)若直线经过A,B两点,请直接写出当时,自变量x的取值的范围是 .
20.市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量(千克)是销售单价(元)的一次函数,且当=40时,=120;=50时,=100.在销售过程中,每天还要支付其他费用500元.
(1)求出与的函数关系式,并写出自变量的取值范围;
(2)求该公司销售该原料日获利(元)与销售单价(元)之间的函数关系式;
(3)当销售单价为多少元时,该公司日获利最大.最大获利是多少元.
21.已知二次函数为常数)的图象经过点,对称轴为直线.
(1)求二次函数的表达式;
(2)若点向上平移2个单位长度,向左平移个单位长度后,恰好落在的图象上,求m的值;
(3)当时,二次函数的最大值与最小值的差为,求n的取值范围.
22.如图,在平面直角坐标系中.抛物线与轴交于两点(点在点的左侧),其顶点为,正方形的边长为5.
(1)点的坐标为________,点的坐标为_______,点的坐标为_______(用含的代数式表示).
(2)当时,抛物线上是否存在点,使 若存在,求出点的坐标.
(3)若抛物线与边只有一个交点,求出的取值范围.
参考答案
1.C
2.B
3.C
4.D
5.C
解:当时,,
则,
∴一元二次方程无实数根,
即函数的图象与轴无交点,
6.B
7.B
解:由图可知a<0,b>0,c>0,
∴b+c>0,
∴点 (a,b+c)位于 第二象限,
8.C
解: 抛物线y=-x2+2x+m 的对称轴为直线,开口向下,
∴当x=1时, y2 最大;
又∵2离对称轴比-1近,
∴ y1 > y3 ,
∴ ,
9.C
解:①当时,设、相交于点M,过点M作于点N,如图,
∵和都是等腰直角三角形,
∴,,
根据平移的性质可知,
∴,,
∴∠AEM=∠MAE=45°,
∴MA=ME,
∴是等腰直角三角形,
∵保持不动,以每秒2个单位长度的速度向右运动,
∴,
∵MN⊥BD,
∴,
∴,
∴函数图象是开口向上的抛物线,
∴y与x的函数关系式的图像是该抛物线位于对称轴y轴右侧图象的一部分,
∴当时,;
②当时,设、交于点P,过点P作于点Q,如图,
同理可得是等腰直角三角形,,
∴,
∴,
∴,
∴,
∴函数图象是开口向上的抛物线,
∴y与x的函数关系式的图像是该抛物线位于对称轴左侧图象的一部分;
综上,ABD不符合题意,C符合题意,
10.D
11.
12.或
13.
14.0或
15.或
解:二次函数y=-x2+2ax-2的对称轴为:,
分以下三种情况:
①当a≤-1时, 在-1≤x≤3内,y随x的增大而减小,
则当x=-1时,取得最大值,最大值为-1-2a-2 =6,
解得:a=,符合题设;
②当-1则当x=a时,y取得最大值,最大值为-a2+2a2-2 =6,
∴a=或x=-(舍去);
③当a≥3时,在-1≤x≤3内,y随x的增大而增大,
则当x=3时,y取得最大值,最大值为-9+6a-2=6,
解得:a=<3,不符合题意,
综上,实数a的值为或.
16.
17.(1)
(2)对称轴为直线,顶点为
18.(1)解:∵把和代入经得:
,解得:
∴直线的解析式是;
把和代入得:
,
解得:
即抛物线为,
(2)解:由(1)知,抛物线为
∴该抛物线顶点D的坐标为;
(3)设直线与抛物线对称轴交于点E,
∵点D的坐标为,
点E的横坐标为,
把代入得,,
,
的面积.
19.(1);
(2),;
(3).
20.(1) y=-2x+200(30≤x≤60);(2) W=-2x2+260x-6500 ;(3) 1900 .
21.(1)解:二次函数为,
抛物线的对称轴为直线.
拋物线
又图象经过点.
抛物线为
(2)解:点B(1,7)向上平移2个单位长度,向左平移m个单位长度(m>0)
平移后的点为(1-m,9)
∵点B(1,7)向上平移2个单位长度,向左平移m个单位长度(m>0)
平移后的点为(1-m,9)代入到y=x2+x+3,
∴9=(1-m)+(-m)+3.
∴m=4或-1
∵m>0
∴m=4
(3)解:当时,;顶点坐标为当时,最大值为5,最小值为.易得关于对称轴的对称点坐标为的取值范围是.
22.(1),,
(2)存在点,使,此时点的坐标为或
(3)的取值范围为或或
1 / 1
一、选择题
1.下列函数中,属于二次函数的是 ( )
A. B. C. D.
2.在平面直角坐标系中,将二次函数的图象向右平移2个单位长度,再向上平移1个单位长度,所得函数的解析式为( )
A. B. C. D.
3.抛物线的顶点坐标( )
A. B. C. D.
4.关于二次函数的图象,下列说法正确的是( )
A.它可由向右平移一个单位得到
B.开口向下
C.顶点坐标是
D.与轴有两个交点
5.函数的图象与轴的交点的情况是( )
A.有两个交点 B.有一个交点 C.没有交点 D.无法判断
6.如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为( )
A.2 B.8 C.10 D.
7.二次函数y=ax2+bx+c的图象如图所示,则点(a,b+c)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知点(2,y1),(1,y2),(-1,y3)在抛物线y=-x2+2x+m上,则( )
A. B. C. D.
9.如图,两个全等的等腰直角和的斜边,点与点.重合,斜边与在一条直线上,保持不动,以每秒2个单位长度的速度向右运动,直到点与点重合时停止运动.设运动时间为秒,两个等腰直角三角形重叠部分的面积为个平方单位,则与函数关系的图象大致是( )
A. B.
C. D.
10.二次函数的图象经过点,向左平移个单位长度后得到新抛物线,直线与新抛物线有两个交点,,则的取值范围为( )
A. B. C. D.
二、填空题
11.二次函数的图象与轴的交点坐标为 .
12.如图,二次函数的图象的对称轴是直线,与x轴的一个交点为,则不等式的解集为 .
13.将抛物线绕顶点旋转后的图象的解析式为 .
14.对于实数,,定义运算“”:;,关于的方程恰好有两个不相等的实数根,则的值是 .
15.函数在有最大值6,则实数的值是 .
16.如图所示,抛物线与轴交于点和点,与轴交于点,且,点、是直线上的两个动点,且(点在点的上方),则四边形的最小值是 .
三、解答题
17.在平面直角坐标系中,抛物线经过和两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴和顶点坐标.
18.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点,与y轴交于点C,直线经过B、C两点,已知,.
(1)求直线和抛物线的解析式;
(2)求抛物线的顶点D的坐标;
(3)求的面积.
19.已知二次函数(如图).
(1)用配方法将化成的形式;
(2)设抛物线与x轴的一个交点为A(非原点),顶点为B,则A点坐标为 ,B点坐标为 ;
(3)若直线经过A,B两点,请直接写出当时,自变量x的取值的范围是 .
20.市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量(千克)是销售单价(元)的一次函数,且当=40时,=120;=50时,=100.在销售过程中,每天还要支付其他费用500元.
(1)求出与的函数关系式,并写出自变量的取值范围;
(2)求该公司销售该原料日获利(元)与销售单价(元)之间的函数关系式;
(3)当销售单价为多少元时,该公司日获利最大.最大获利是多少元.
21.已知二次函数为常数)的图象经过点,对称轴为直线.
(1)求二次函数的表达式;
(2)若点向上平移2个单位长度,向左平移个单位长度后,恰好落在的图象上,求m的值;
(3)当时,二次函数的最大值与最小值的差为,求n的取值范围.
22.如图,在平面直角坐标系中.抛物线与轴交于两点(点在点的左侧),其顶点为,正方形的边长为5.
(1)点的坐标为________,点的坐标为_______,点的坐标为_______(用含的代数式表示).
(2)当时,抛物线上是否存在点,使 若存在,求出点的坐标.
(3)若抛物线与边只有一个交点,求出的取值范围.
参考答案
1.C
2.B
3.C
4.D
5.C
解:当时,,
则,
∴一元二次方程无实数根,
即函数的图象与轴无交点,
6.B
7.B
解:由图可知a<0,b>0,c>0,
∴b+c>0,
∴点 (a,b+c)位于 第二象限,
8.C
解: 抛物线y=-x2+2x+m 的对称轴为直线,开口向下,
∴当x=1时, y2 最大;
又∵2离对称轴比-1近,
∴ y1 > y3 ,
∴ ,
9.C
解:①当时,设、相交于点M,过点M作于点N,如图,
∵和都是等腰直角三角形,
∴,,
根据平移的性质可知,
∴,,
∴∠AEM=∠MAE=45°,
∴MA=ME,
∴是等腰直角三角形,
∵保持不动,以每秒2个单位长度的速度向右运动,
∴,
∵MN⊥BD,
∴,
∴,
∴函数图象是开口向上的抛物线,
∴y与x的函数关系式的图像是该抛物线位于对称轴y轴右侧图象的一部分,
∴当时,;
②当时,设、交于点P,过点P作于点Q,如图,
同理可得是等腰直角三角形,,
∴,
∴,
∴,
∴,
∴函数图象是开口向上的抛物线,
∴y与x的函数关系式的图像是该抛物线位于对称轴左侧图象的一部分;
综上,ABD不符合题意,C符合题意,
10.D
11.
12.或
13.
14.0或
15.或
解:二次函数y=-x2+2ax-2的对称轴为:,
分以下三种情况:
①当a≤-1时, 在-1≤x≤3内,y随x的增大而减小,
则当x=-1时,取得最大值,最大值为-1-2a-2 =6,
解得:a=,符合题设;
②当-1
∴a=或x=-(舍去);
③当a≥3时,在-1≤x≤3内,y随x的增大而增大,
则当x=3时,y取得最大值,最大值为-9+6a-2=6,
解得:a=<3,不符合题意,
综上,实数a的值为或.
16.
17.(1)
(2)对称轴为直线,顶点为
18.(1)解:∵把和代入经得:
,解得:
∴直线的解析式是;
把和代入得:
,
解得:
即抛物线为,
(2)解:由(1)知,抛物线为
∴该抛物线顶点D的坐标为;
(3)设直线与抛物线对称轴交于点E,
∵点D的坐标为,
点E的横坐标为,
把代入得,,
,
的面积.
19.(1);
(2),;
(3).
20.(1) y=-2x+200(30≤x≤60);(2) W=-2x2+260x-6500 ;(3) 1900 .
21.(1)解:二次函数为,
抛物线的对称轴为直线.
拋物线
又图象经过点.
抛物线为
(2)解:点B(1,7)向上平移2个单位长度,向左平移m个单位长度(m>0)
平移后的点为(1-m,9)
∵点B(1,7)向上平移2个单位长度,向左平移m个单位长度(m>0)
平移后的点为(1-m,9)代入到y=x2+x+3,
∴9=(1-m)+(-m)+3.
∴m=4或-1
∵m>0
∴m=4
(3)解:当时,;顶点坐标为当时,最大值为5,最小值为.易得关于对称轴的对称点坐标为的取值范围是.
22.(1),,
(2)存在点,使,此时点的坐标为或
(3)的取值范围为或或
1 / 1
同课章节目录
