1.3解直角三角形
图片预览


文档简介
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成
1.3解直角三角形
一、单选题
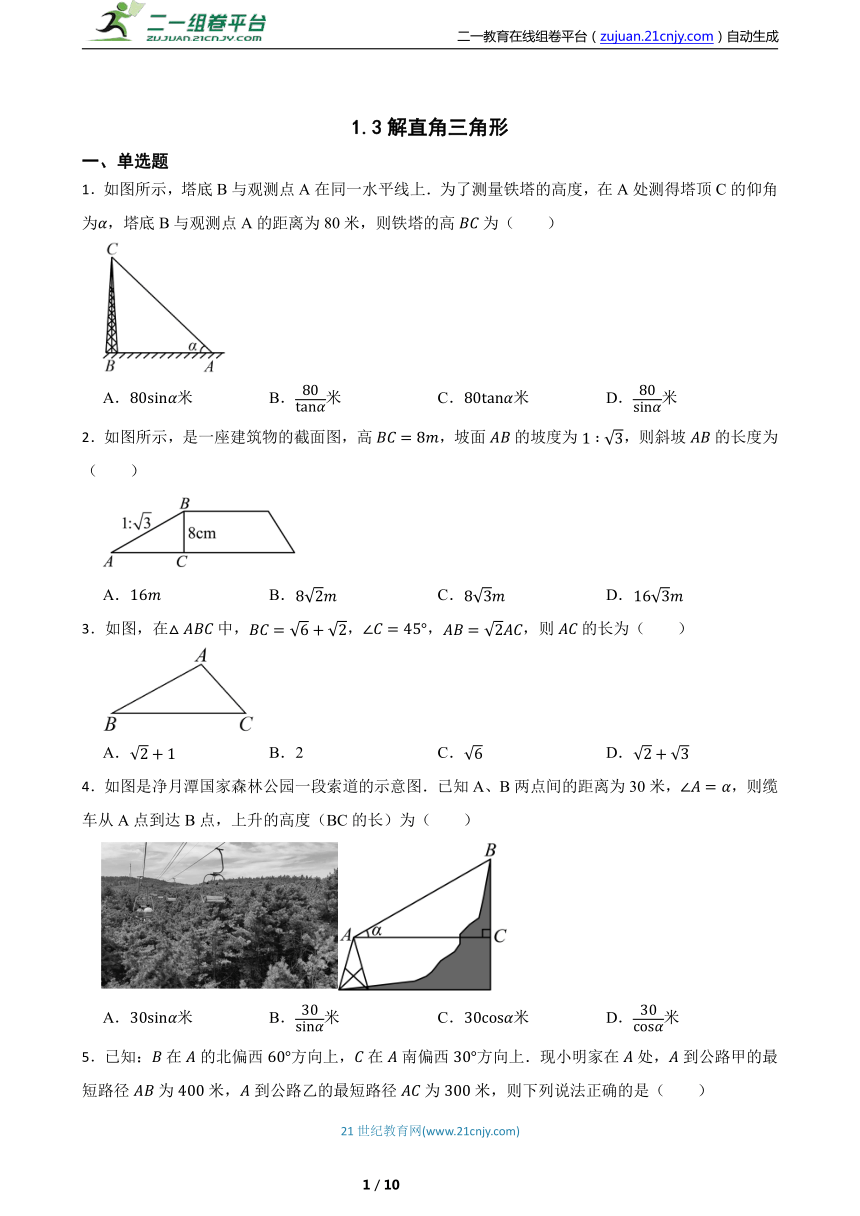
1.如图所示,塔底B与观测点A在同一水平线上.为了测量铁塔的高度,在A处测得塔顶C的仰角为,塔底B与观测点A的距离为80米,则铁塔的高为( )
A.米 B.米 C.米 D.米
2.如图所示,是一座建筑物的截面图,高,坡面的坡度为,则斜坡的长度为( )
A. B. C. D.
3.如图,在中,,,,则的长为( )
A. B.2 C. D.
4.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.米 B.米 C.米 D.米
5.已知:在的北偏西方向上,在南偏西方向上.现小明家在处,到公路甲的最短路径为米,到公路乙的最短路径为米,则下列说法正确的是( )
A.甲、乙两条路径互相垂直 B.,两点之间的距离为米
C.,两点之间的距离为米 D.甲、乙两条路径互相平行
6.有一题目:“如图,在四边形中,,,,,将边绕点逆时针旋转角得到,连接,.当为直角三角形时,求旋转角的度数.”嘉嘉说:“角为.”而淇淇说:“嘉嘉考虑的不周全,角还应有另外两个不同的值.”下列判断正确的是( )
A.淇淇说的对,且角的另外两个值是,
B.淇淇说的对,且角的另外两个值是,
C.淇淇说的不对,角就得
D.两人都不对,角仅有2个不同值
7.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度BC为( )
A. B.
C. D.
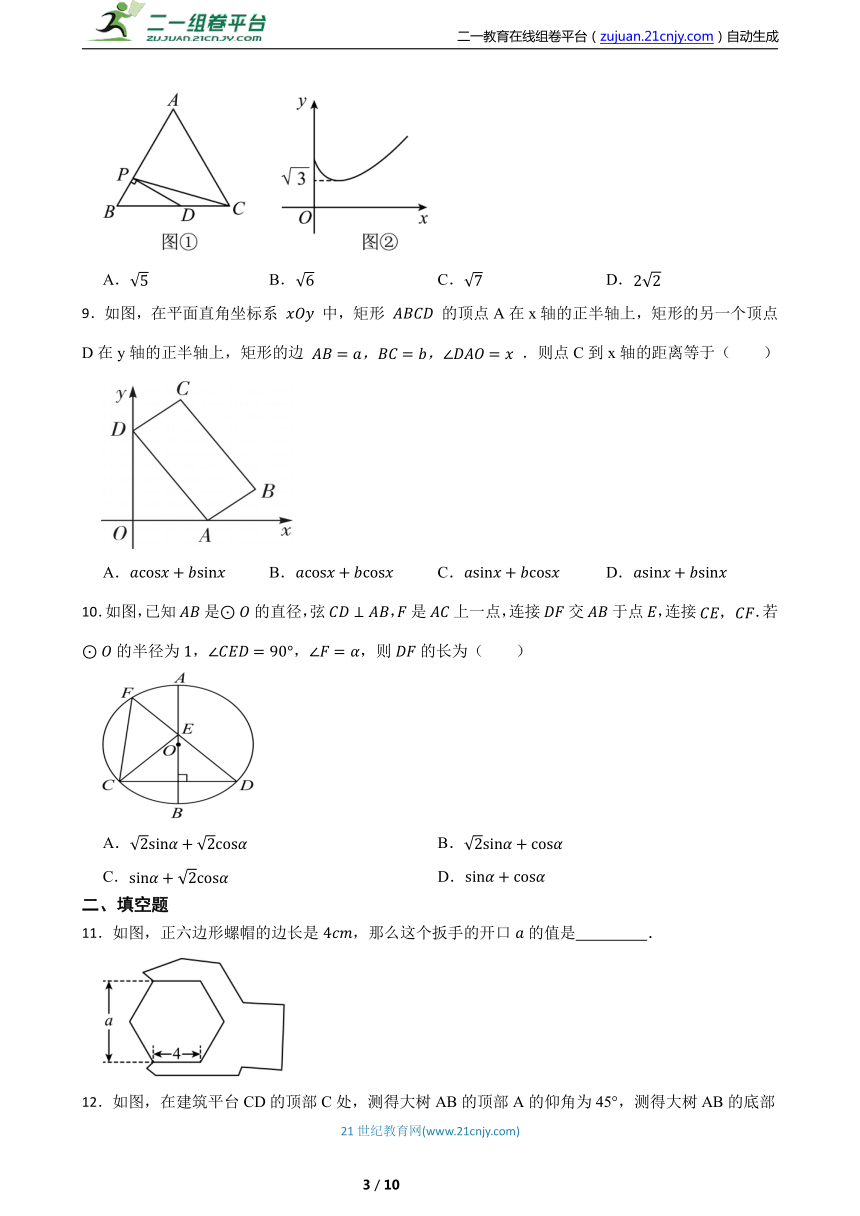
8.如图,在等边中,点D是边的三等分点,连接,设,图①中,其中一条线段的长为y.运动过程中y与x函数关系的图象如图②所示,则长为( )
A. B. C. D.
9.如图,在平面直角坐标系 中,矩形 的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边 .则点C到x轴的距离等于( )
A. B. C. D.
10.如图,已知是的直径,弦,是上一点,连接交于点,连接.若的半径为,,,则的长为( )
A. B.
C. D.
二、填空题
11.如图,正六边形螺帽的边长是,那么这个扳手的开口的值是 .
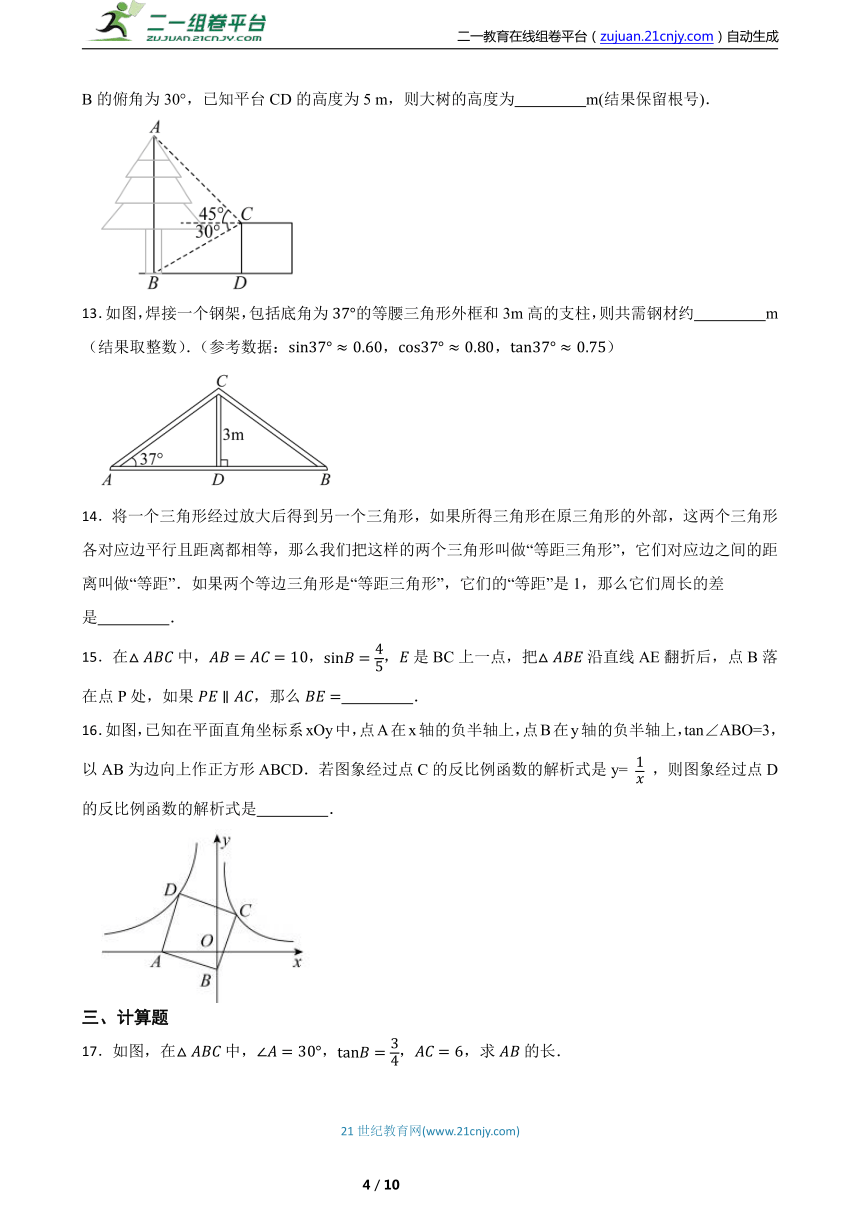
12.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5 m,则大树的高度为 m(结果保留根号).
13.如图,焊接一个钢架,包括底角为的等腰三角形外框和3m高的支柱,则共需钢材约 m(结果取整数).(参考数据:,,)
14.将一个三角形经过放大后得到另一个三角形,如果所得三角形在原三角形的外部,这两个三角形各对应边平行且距离都相等,那么我们把这样的两个三角形叫做“等距三角形”,它们对应边之间的距离叫做“等距”.如果两个等边三角形是“等距三角形”,它们的“等距”是1,那么它们周长的差是 .
15.在中,,,是BC上一点,把沿直线AE翻折后,点B落在点P处,如果,那么 .
16.如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .
三、计算题
17.如图,在中,,,,求的长.
18.如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
19.如图1,已知抛物线与轴交于、两点(点在点左边),与轴交于点,其中.
(1)求线段的长度.
(2)如图,点是直线上方抛物线上的一动点,过点作轴交于点,作轴交于点,为中点,连接,请求出的最大值以及此时点的坐标.
(3)将抛物线水平向右平移个单位后得到抛物线,点、点的对应点分别为点、点,抛物线与轴交于点(点不与原点重合),连接、.在平移过程中,当时,请直接写出的值.
四、解答题
20.某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动.如图,此时无人机在离地面20 m的点A处,无人机测得教学楼底部B处的俯角为53°,测得教学楼顶部C处的俯角为30°.求教学楼的高(结果保留一位小数.参考数据:.)
21.如图,长500米的水库大坝的横断面是梯形,坝顶宽,坝高,斜坡的坡比,斜坡的坡比,
(1)求坝底宽的长
(2)修筑这个堤坝需要土方多少立方米?
22.某学校升气球庆祝党的二十大胜利召开.如图,一气球到达离地面高度为12米的处时,仪器显示正前方一高楼顶部的仰角是,底部的俯角是.气球要飞到楼顶,应至少再上升多少米?(结果精确到0.1米)(参考数据:,,,)
23.如图,在平面直角坐标系中,菱形的边在x轴上,,的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点E和点F,动点N从点E以每秒2个单位长度的速度沿向终点F运动.设运动时间为t秒.
(1)求直线的函数表达式:
(2)求点N到直线的距离h与运动时间t的函数关系式,直接写出自变量的取值范围;
(3)点N在运动的过程中,在坐标平面内是否存在一点M.使得以为顶点的四边形是矩形.若存在,直接写出点M的坐标,若不存在,说明理由.
答案解析部分
1.【答案】C
【知识点】解直角三角形的实际应用﹣仰角俯角问题
2.【答案】A
【知识点】含30°角的直角三角形;解直角三角形的实际应用﹣坡度坡角问题
3.【答案】B
【知识点】勾股定理;解直角三角形
4.【答案】A
【知识点】解直角三角形的其他实际应用
5.【答案】A
【知识点】勾股定理;解直角三角形的实际应用﹣方向角问题
6.【答案】B
【知识点】解直角三角形;旋转的性质
7.【答案】C
【知识点】解直角三角形的实际应用﹣坡度坡角问题
8.【答案】C
【知识点】等边三角形的性质;解直角三角形
9.【答案】A
【知识点】矩形的性质;解直角三角形
10.【答案】A
【知识点】线段垂直平分线的性质;垂径定理;圆周角定理;解直角三角形
11.【答案】
【知识点】解直角三角形
12.【答案】5+5
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】21
【知识点】解直角三角形的其他实际应用
14.【答案】
【知识点】解直角三角形
15.【答案】2
【知识点】等腰三角形的性质;解直角三角形
16.【答案】y=
【知识点】解直角三角形;反比例函数图象上点的坐标特征;三角形全等的判定-AAS
17.【答案】
【知识点】解直角三角形
18.【答案】.
【知识点】解直角三角形的实际应用﹣方向角问题
19.【答案】(1);
(2);;
(3),.
【知识点】解直角三角形
20.【答案】建筑物的高约为11.4m
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】(1)
(2)(立方米)
【知识点】解直角三角形的实际应用﹣坡度坡角问题
22.【答案】解:过作,垂足为点,过作,垂足为点,
根据题意,楼,
∴四边形是矩形,
∴,和都是直角三角形,
∵气球到达离地面高度为12米的处时,仪器显示正前方高楼顶部的仰角是,底部的俯角是,
∴,,,
在中,
∵,.
∴,
在中,
∵,.
∴(米).
答:气球应至少再上升5.2米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
23.【答案】(1)
(2)
(3)存在,点M的坐标是或
【知识点】菱形的性质;平移的性质;解直角三角形;一次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
1 / 10
1.3解直角三角形
一、单选题
1.如图所示,塔底B与观测点A在同一水平线上.为了测量铁塔的高度,在A处测得塔顶C的仰角为,塔底B与观测点A的距离为80米,则铁塔的高为( )
A.米 B.米 C.米 D.米
2.如图所示,是一座建筑物的截面图,高,坡面的坡度为,则斜坡的长度为( )
A. B. C. D.
3.如图,在中,,,,则的长为( )
A. B.2 C. D.
4.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.米 B.米 C.米 D.米
5.已知:在的北偏西方向上,在南偏西方向上.现小明家在处,到公路甲的最短路径为米,到公路乙的最短路径为米,则下列说法正确的是( )
A.甲、乙两条路径互相垂直 B.,两点之间的距离为米
C.,两点之间的距离为米 D.甲、乙两条路径互相平行
6.有一题目:“如图,在四边形中,,,,,将边绕点逆时针旋转角得到,连接,.当为直角三角形时,求旋转角的度数.”嘉嘉说:“角为.”而淇淇说:“嘉嘉考虑的不周全,角还应有另外两个不同的值.”下列判断正确的是( )
A.淇淇说的对,且角的另外两个值是,
B.淇淇说的对,且角的另外两个值是,
C.淇淇说的不对,角就得
D.两人都不对,角仅有2个不同值
7.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度BC为( )
A. B.
C. D.
8.如图,在等边中,点D是边的三等分点,连接,设,图①中,其中一条线段的长为y.运动过程中y与x函数关系的图象如图②所示,则长为( )
A. B. C. D.
9.如图,在平面直角坐标系 中,矩形 的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边 .则点C到x轴的距离等于( )
A. B. C. D.
10.如图,已知是的直径,弦,是上一点,连接交于点,连接.若的半径为,,,则的长为( )
A. B.
C. D.
二、填空题
11.如图,正六边形螺帽的边长是,那么这个扳手的开口的值是 .
12.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5 m,则大树的高度为 m(结果保留根号).
13.如图,焊接一个钢架,包括底角为的等腰三角形外框和3m高的支柱,则共需钢材约 m(结果取整数).(参考数据:,,)
14.将一个三角形经过放大后得到另一个三角形,如果所得三角形在原三角形的外部,这两个三角形各对应边平行且距离都相等,那么我们把这样的两个三角形叫做“等距三角形”,它们对应边之间的距离叫做“等距”.如果两个等边三角形是“等距三角形”,它们的“等距”是1,那么它们周长的差是 .
15.在中,,,是BC上一点,把沿直线AE翻折后,点B落在点P处,如果,那么 .
16.如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .
三、计算题
17.如图,在中,,,,求的长.
18.如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
19.如图1,已知抛物线与轴交于、两点(点在点左边),与轴交于点,其中.
(1)求线段的长度.
(2)如图,点是直线上方抛物线上的一动点,过点作轴交于点,作轴交于点,为中点,连接,请求出的最大值以及此时点的坐标.
(3)将抛物线水平向右平移个单位后得到抛物线,点、点的对应点分别为点、点,抛物线与轴交于点(点不与原点重合),连接、.在平移过程中,当时,请直接写出的值.
四、解答题
20.某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动.如图,此时无人机在离地面20 m的点A处,无人机测得教学楼底部B处的俯角为53°,测得教学楼顶部C处的俯角为30°.求教学楼的高(结果保留一位小数.参考数据:.)
21.如图,长500米的水库大坝的横断面是梯形,坝顶宽,坝高,斜坡的坡比,斜坡的坡比,
(1)求坝底宽的长
(2)修筑这个堤坝需要土方多少立方米?
22.某学校升气球庆祝党的二十大胜利召开.如图,一气球到达离地面高度为12米的处时,仪器显示正前方一高楼顶部的仰角是,底部的俯角是.气球要飞到楼顶,应至少再上升多少米?(结果精确到0.1米)(参考数据:,,,)
23.如图,在平面直角坐标系中,菱形的边在x轴上,,的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点E和点F,动点N从点E以每秒2个单位长度的速度沿向终点F运动.设运动时间为t秒.
(1)求直线的函数表达式:
(2)求点N到直线的距离h与运动时间t的函数关系式,直接写出自变量的取值范围;
(3)点N在运动的过程中,在坐标平面内是否存在一点M.使得以为顶点的四边形是矩形.若存在,直接写出点M的坐标,若不存在,说明理由.
答案解析部分
1.【答案】C
【知识点】解直角三角形的实际应用﹣仰角俯角问题
2.【答案】A
【知识点】含30°角的直角三角形;解直角三角形的实际应用﹣坡度坡角问题
3.【答案】B
【知识点】勾股定理;解直角三角形
4.【答案】A
【知识点】解直角三角形的其他实际应用
5.【答案】A
【知识点】勾股定理;解直角三角形的实际应用﹣方向角问题
6.【答案】B
【知识点】解直角三角形;旋转的性质
7.【答案】C
【知识点】解直角三角形的实际应用﹣坡度坡角问题
8.【答案】C
【知识点】等边三角形的性质;解直角三角形
9.【答案】A
【知识点】矩形的性质;解直角三角形
10.【答案】A
【知识点】线段垂直平分线的性质;垂径定理;圆周角定理;解直角三角形
11.【答案】
【知识点】解直角三角形
12.【答案】5+5
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】21
【知识点】解直角三角形的其他实际应用
14.【答案】
【知识点】解直角三角形
15.【答案】2
【知识点】等腰三角形的性质;解直角三角形
16.【答案】y=
【知识点】解直角三角形;反比例函数图象上点的坐标特征;三角形全等的判定-AAS
17.【答案】
【知识点】解直角三角形
18.【答案】.
【知识点】解直角三角形的实际应用﹣方向角问题
19.【答案】(1);
(2);;
(3),.
【知识点】解直角三角形
20.【答案】建筑物的高约为11.4m
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】(1)
(2)(立方米)
【知识点】解直角三角形的实际应用﹣坡度坡角问题
22.【答案】解:过作,垂足为点,过作,垂足为点,
根据题意,楼,
∴四边形是矩形,
∴,和都是直角三角形,
∵气球到达离地面高度为12米的处时,仪器显示正前方高楼顶部的仰角是,底部的俯角是,
∴,,,
在中,
∵,.
∴,
在中,
∵,.
∴(米).
答:气球应至少再上升5.2米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
23.【答案】(1)
(2)
(3)存在,点M的坐标是或
【知识点】菱形的性质;平移的性质;解直角三角形;一次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
1 / 10
