第一章解直角三角形综合题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章解直角三角形综合题
一、填空题
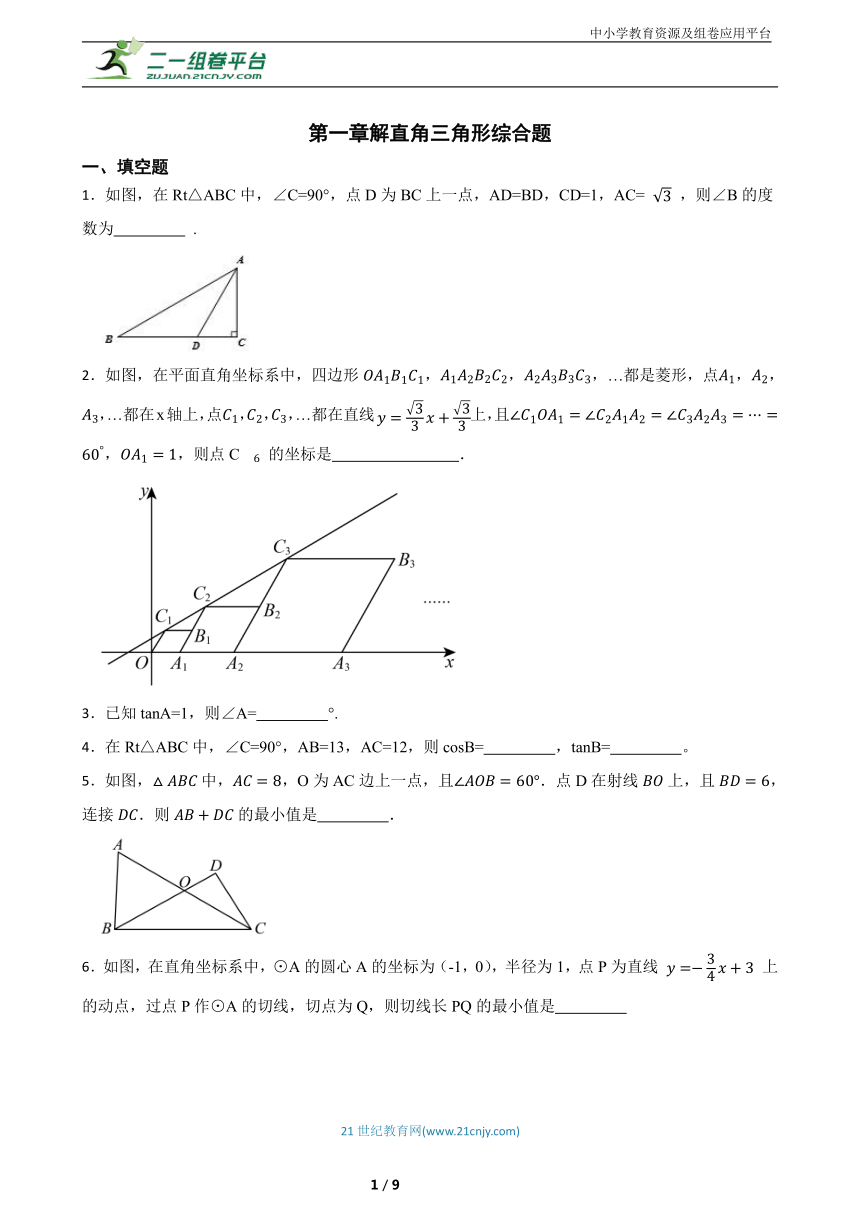
1.如图,在Rt△ABC中,∠C=90°,点D为BC上一点,AD=BD,CD=1,AC= ,则∠B的度数为 .
2.如图,在平面直角坐标系中,四边形,,,…都是菱形,点,,,…都在x轴上,点,,,…都在直线上,且,,则点C 的坐标是 .
3.已知tanA=1,则∠A= °.
4.在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosB= ,tanB= 。
5.如图,中,,O为AC边上一点,且.点D在射线上,且,连接.则的最小值是 .
6.如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线 上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
二、单选题
7.如图,以为圆心,任意长为半径画弧,与射线交于点,再以为圆心,长为半径画弧,两弧交于点,画射线,则( )
A. B. C. D.
8.如图所示,某博物馆大厅电梯的截面图中,AB的长为12 m,AB与AC的夹角为α,则高BC是( )
A.12sin α m B.12cos α m C. m D. m
9.如图,要测量河两相对的两点P、A之间的距离,可以在AP的垂线PB上取点C,测得PC=100米,用测角仪测得∠ACP=40°,则AP的长为( )
A.100sin40°米 B.100tan40°米
C. 米 D. 米
10.图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,,则双翼边缘端点C与D之间的距离为( )
A. B.
C. D.
11.如图,Rt△ABC中,∠ACB=90°,AB=5,AC=4,CD⊥AB于D,则tan∠BCD的值为( )
A. B. C. D.
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,∠CDB=30°,CD=4,则阴影部分的面积为( )
A.π B.4π C.π D.π
13.sin60°的值等于( )
A. B. C. D.
14.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
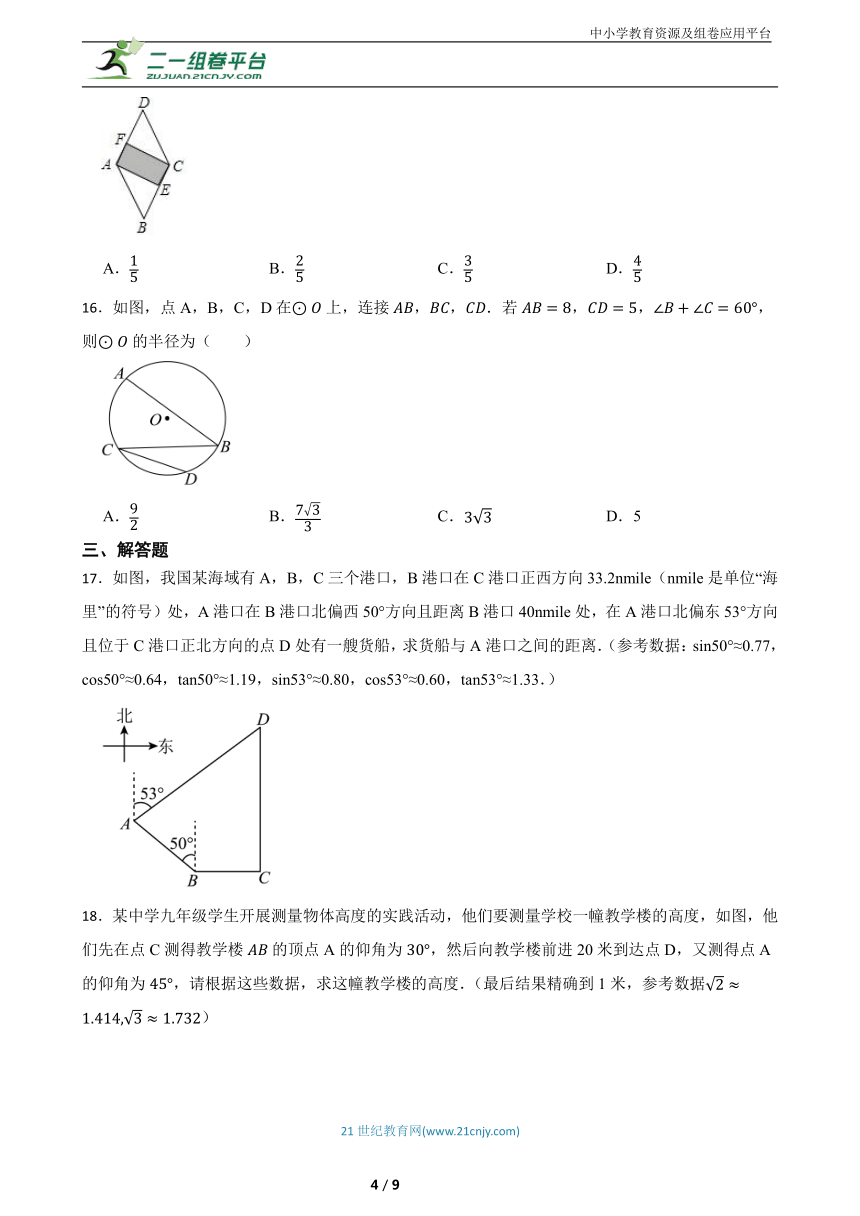
15.如图,将一块菱形ABCD硬纸片固定后进行投针训练.已知纸片上AE⊥BC于E,CF⊥AD于F,sinD= .若随意投出一针命中了菱形纸片,则命中矩形区域的概率是( )
A. B. C. D.
16.如图,点A,B,C,D在上,连接,,.若,,,则的半径为( )
A. B. C. D.5
三、解答题
17.如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
18.某中学九年级学生开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度,如图,他们先在点C测得教学楼的顶点A的仰角为,然后向教学楼前进20米到达点D,又测得点A的仰角为,请根据这些数据,求这幢教学楼的高度.(最后结果精确到1米,参考数据)
19.如图,小明站在斜坡AB上的点A处,看到坡下一棵大树顶端的影子刚好落在山脚下的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60°角,在点A处测得大树顶端的俯角为15°.已知山坡AB的坡比为,AB为10米,请帮助小明计算这棵大树的高度.(结果精确到0.1米,参考数据:)
20.如图,二次函数的图像与x轴交于点A,B(点A在点B的左侧),且,与y轴交于点C.点P是第四象限抛物线上一点,过点P作轴,垂足为D,交直线于点E.
(1)填空:______;
(2)若是以为底边的等腰三角形,求点P的坐标;
(3)连接,过点P作直线交y轴正半轴于点F,若,求点P的横坐标.
四、计算题
21.计算: .
22.计算:
23.如图,在平面直角坐标系中,抛物线与轴交于点,点,交轴于点.
(1)求抛物线的解析式;
(2)如图,连接,过点作射线交轴的正半轴于点,点与点关于原点对称,点是第四象限抛物线上一动点,过点作的垂线交于点,求线段长度的最大值及此时点的坐标;
(3)如图,把点向上平移个单位得到点,连接,把绕点顺时针旋转一定的角度,得到,其中边交坐标轴于点,在旋转过程中,是否存在一点,使得?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】30°
【知识点】解直角三角形
2.【答案】(47,16)
【知识点】菱形的判定与性质;解直角三角形
3.【答案】45
【知识点】求特殊角的三角函数值
4.【答案】;
【知识点】锐角三角函数的定义
5.【答案】
【知识点】三角形三边关系;勾股定理;平行四边形的性质;解直角三角形
6.【答案】2
【知识点】点到直线的距离;勾股定理的应用;解直角三角形
7.【答案】B
【知识点】求特殊角的三角函数值
8.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
9.【答案】B
【知识点】解直角三角形的其他实际应用
10.【答案】D
【知识点】解直角三角形的其他实际应用
11.【答案】D
【知识点】解直角三角形
12.【答案】D
【知识点】等边三角形的判定与性质;垂径定理;扇形面积的计算;解直角三角形
13.【答案】C
【知识点】求特殊角的三角函数值
14.【答案】D
【知识点】勾股定理;圆周角定理;锐角三角函数的定义
15.【答案】B
【知识点】锐角三角函数的定义;几何概率
16.【答案】B
【知识点】勾股定理;垂径定理;圆周角定理;解直角三角形
17.【答案】货船与A港口之间的距离约为80海里
【知识点】解直角三角形的实际应用﹣方向角问题
18.【答案】27米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
19.【答案】解:过D作DM⊥AB于M,过A作AF⊥BC于F,
∵山坡AB的坡比为,
∴tan∠ABF=,
∴∠ABF=60°,
∴∠ABD=180°-∠ABF-∠DBC=60°,
∴在Rt△MBD中,
tan∠MBD=,
设MB=x,则MD=x,
∵AE∥CB,
∴∠EAB=∠ABF=60°,
∴∠DAM=∠EAM-∠EAD=45°,
在Rt△AMD中,
tan∠MAD==1,
∴AM=MD=x,
∴x+x=10,
∴x=5-5,
在Rt△MBD中,cos∠MBD==,
∴BD=2x=10-10,
∵sin∠DBC==,
∴DC=15-5≈6.3(米),
答:这棵大树的高度约为6.3米.
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
20.【答案】(1)
(2)
(3)点P的横坐标是4
【知识点】待定系数法求二次函数解析式;等腰三角形的性质;解直角三角形
21.【答案】
【知识点】零指数幂;二次根式的混合运算;求特殊角的三角函数值
22.【答案】解:原式=1-3- 2+1+3
=
【知识点】求特殊角的三角函数值;实数的混合运算(含开方)
23.【答案】(1)抛物线的解析式为;
(2),此时;
(3).
【知识点】待定系数法求二次函数解析式;解直角三角形;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 9
第一章解直角三角形综合题
一、填空题
1.如图,在Rt△ABC中,∠C=90°,点D为BC上一点,AD=BD,CD=1,AC= ,则∠B的度数为 .
2.如图,在平面直角坐标系中,四边形,,,…都是菱形,点,,,…都在x轴上,点,,,…都在直线上,且,,则点C 的坐标是 .
3.已知tanA=1,则∠A= °.
4.在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosB= ,tanB= 。
5.如图,中,,O为AC边上一点,且.点D在射线上,且,连接.则的最小值是 .
6.如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线 上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
二、单选题
7.如图,以为圆心,任意长为半径画弧,与射线交于点,再以为圆心,长为半径画弧,两弧交于点,画射线,则( )
A. B. C. D.
8.如图所示,某博物馆大厅电梯的截面图中,AB的长为12 m,AB与AC的夹角为α,则高BC是( )
A.12sin α m B.12cos α m C. m D. m
9.如图,要测量河两相对的两点P、A之间的距离,可以在AP的垂线PB上取点C,测得PC=100米,用测角仪测得∠ACP=40°,则AP的长为( )
A.100sin40°米 B.100tan40°米
C. 米 D. 米
10.图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,,则双翼边缘端点C与D之间的距离为( )
A. B.
C. D.
11.如图,Rt△ABC中,∠ACB=90°,AB=5,AC=4,CD⊥AB于D,则tan∠BCD的值为( )
A. B. C. D.
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,∠CDB=30°,CD=4,则阴影部分的面积为( )
A.π B.4π C.π D.π
13.sin60°的值等于( )
A. B. C. D.
14.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
15.如图,将一块菱形ABCD硬纸片固定后进行投针训练.已知纸片上AE⊥BC于E,CF⊥AD于F,sinD= .若随意投出一针命中了菱形纸片,则命中矩形区域的概率是( )
A. B. C. D.
16.如图,点A,B,C,D在上,连接,,.若,,,则的半径为( )
A. B. C. D.5
三、解答题
17.如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
18.某中学九年级学生开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度,如图,他们先在点C测得教学楼的顶点A的仰角为,然后向教学楼前进20米到达点D,又测得点A的仰角为,请根据这些数据,求这幢教学楼的高度.(最后结果精确到1米,参考数据)
19.如图,小明站在斜坡AB上的点A处,看到坡下一棵大树顶端的影子刚好落在山脚下的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60°角,在点A处测得大树顶端的俯角为15°.已知山坡AB的坡比为,AB为10米,请帮助小明计算这棵大树的高度.(结果精确到0.1米,参考数据:)
20.如图,二次函数的图像与x轴交于点A,B(点A在点B的左侧),且,与y轴交于点C.点P是第四象限抛物线上一点,过点P作轴,垂足为D,交直线于点E.
(1)填空:______;
(2)若是以为底边的等腰三角形,求点P的坐标;
(3)连接,过点P作直线交y轴正半轴于点F,若,求点P的横坐标.
四、计算题
21.计算: .
22.计算:
23.如图,在平面直角坐标系中,抛物线与轴交于点,点,交轴于点.
(1)求抛物线的解析式;
(2)如图,连接,过点作射线交轴的正半轴于点,点与点关于原点对称,点是第四象限抛物线上一动点,过点作的垂线交于点,求线段长度的最大值及此时点的坐标;
(3)如图,把点向上平移个单位得到点,连接,把绕点顺时针旋转一定的角度,得到,其中边交坐标轴于点,在旋转过程中,是否存在一点,使得?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】30°
【知识点】解直角三角形
2.【答案】(47,16)
【知识点】菱形的判定与性质;解直角三角形
3.【答案】45
【知识点】求特殊角的三角函数值
4.【答案】;
【知识点】锐角三角函数的定义
5.【答案】
【知识点】三角形三边关系;勾股定理;平行四边形的性质;解直角三角形
6.【答案】2
【知识点】点到直线的距离;勾股定理的应用;解直角三角形
7.【答案】B
【知识点】求特殊角的三角函数值
8.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
9.【答案】B
【知识点】解直角三角形的其他实际应用
10.【答案】D
【知识点】解直角三角形的其他实际应用
11.【答案】D
【知识点】解直角三角形
12.【答案】D
【知识点】等边三角形的判定与性质;垂径定理;扇形面积的计算;解直角三角形
13.【答案】C
【知识点】求特殊角的三角函数值
14.【答案】D
【知识点】勾股定理;圆周角定理;锐角三角函数的定义
15.【答案】B
【知识点】锐角三角函数的定义;几何概率
16.【答案】B
【知识点】勾股定理;垂径定理;圆周角定理;解直角三角形
17.【答案】货船与A港口之间的距离约为80海里
【知识点】解直角三角形的实际应用﹣方向角问题
18.【答案】27米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
19.【答案】解:过D作DM⊥AB于M,过A作AF⊥BC于F,
∵山坡AB的坡比为,
∴tan∠ABF=,
∴∠ABF=60°,
∴∠ABD=180°-∠ABF-∠DBC=60°,
∴在Rt△MBD中,
tan∠MBD=,
设MB=x,则MD=x,
∵AE∥CB,
∴∠EAB=∠ABF=60°,
∴∠DAM=∠EAM-∠EAD=45°,
在Rt△AMD中,
tan∠MAD==1,
∴AM=MD=x,
∴x+x=10,
∴x=5-5,
在Rt△MBD中,cos∠MBD==,
∴BD=2x=10-10,
∵sin∠DBC==,
∴DC=15-5≈6.3(米),
答:这棵大树的高度约为6.3米.
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
20.【答案】(1)
(2)
(3)点P的横坐标是4
【知识点】待定系数法求二次函数解析式;等腰三角形的性质;解直角三角形
21.【答案】
【知识点】零指数幂;二次根式的混合运算;求特殊角的三角函数值
22.【答案】解:原式=1-3- 2+1+3
=
【知识点】求特殊角的三角函数值;实数的混合运算(含开方)
23.【答案】(1)抛物线的解析式为;
(2),此时;
(3).
【知识点】待定系数法求二次函数解析式;解直角三角形;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 9
