2.1直线和圆的位置关系(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
2.1直线和圆的位置关系
一、单选题
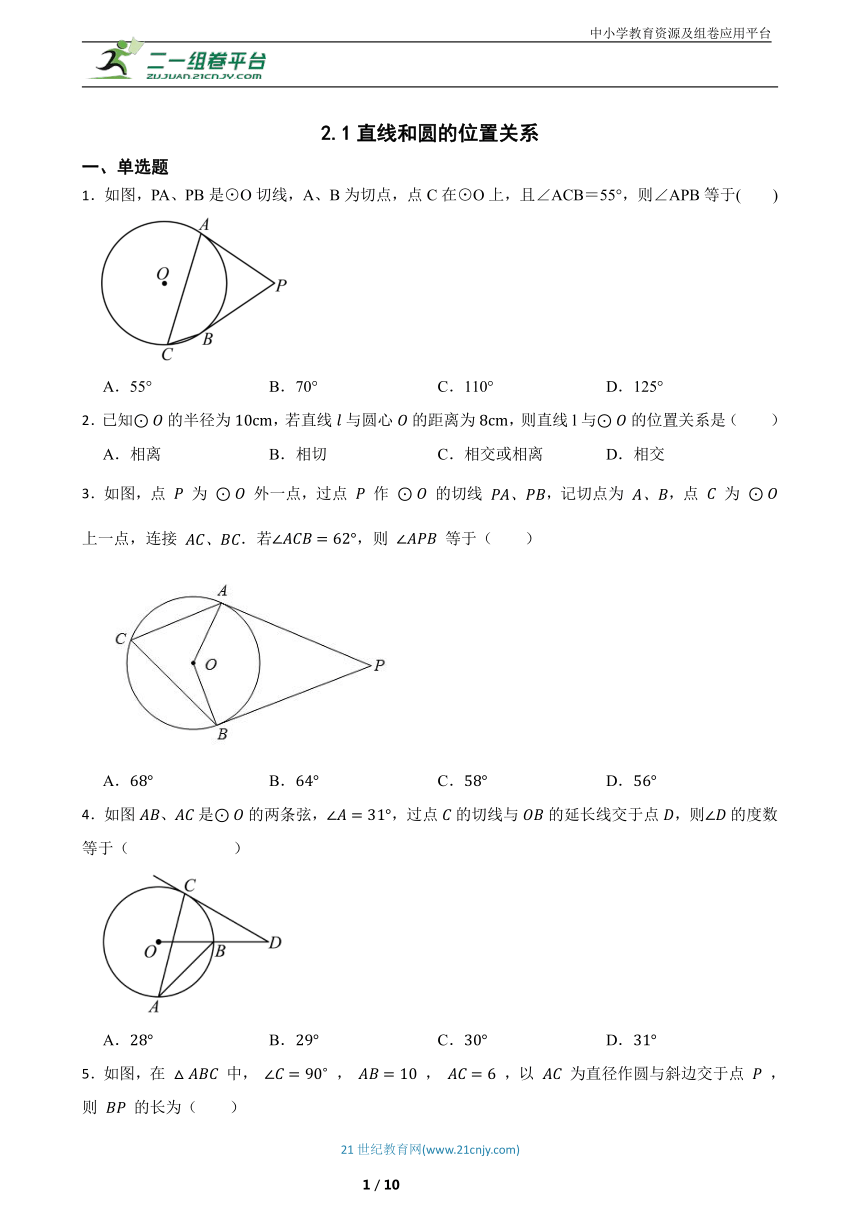
1.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )
A.55° B.70° C.110° D.125°
2.已知的半径为,若直线与圆心的距离为,则直线l与的位置关系是( )
A.相离 B.相切 C.相交或相离 D.相交
3.如图,点 为 外一点,过点 作 的切线 ,记切点为 ,点 为 上一点,连接 .若,则 等于( )
A. B. C. D.
4.如图、是的两条弦,,过点的切线与的延长线交于点,则的度数等于( )
A. B. C. D.
5.如图,在 中, , , ,以 为直径作圆与斜边交于点 ,则 的长为( )
A. B. C. D.
二、填空题
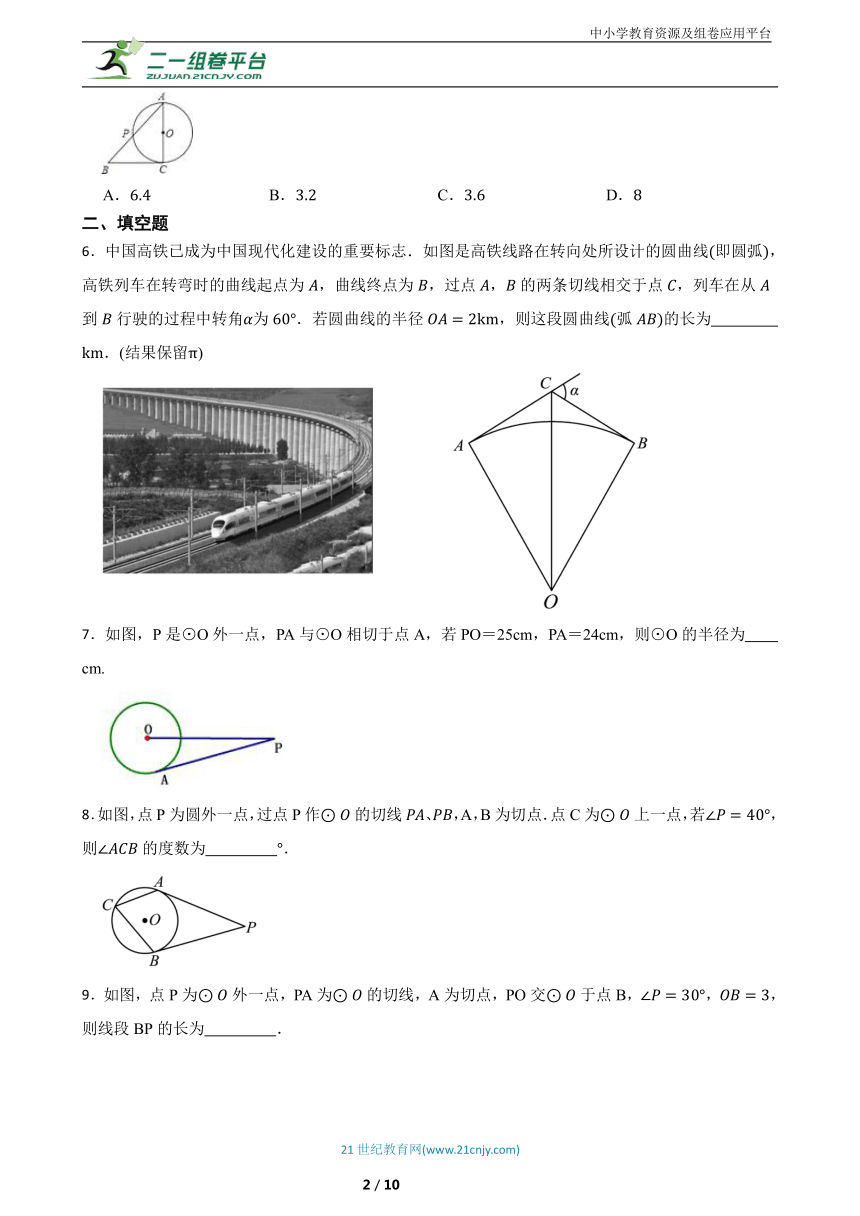
6.中国高铁已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线即圆弧,高铁列车在转弯时的曲线起点为,曲线终点为,过点,的两条切线相交于点,列车在从到行驶的过程中转角为.若圆曲线的半径,则这段圆曲线弧的长为 .(结果保留)
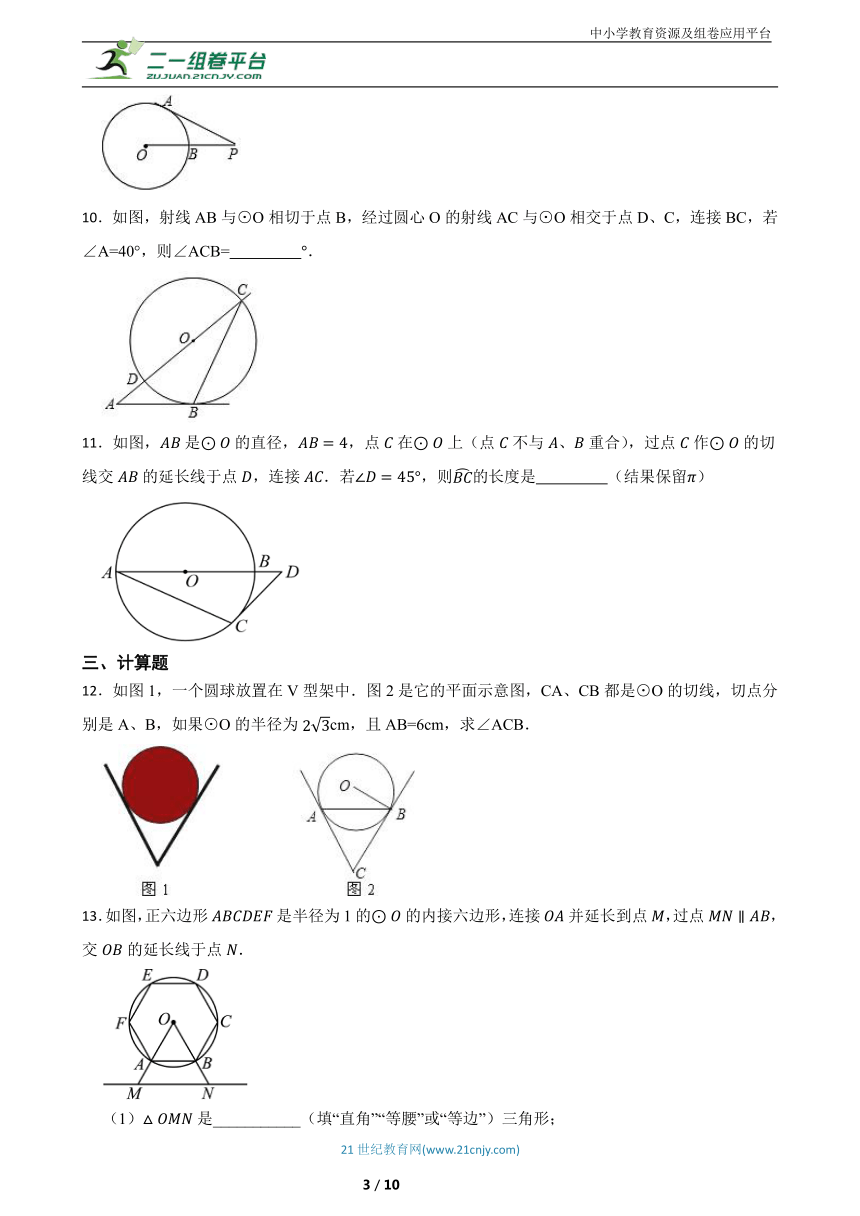
7.如图,P是⊙O外一点,PA与⊙O相切于点A,若PO=25cm,PA=24cm,则⊙O的半径为 cm.
8.如图,点P为圆外一点,过点P作的切线、,A,B为切点.点C为上一点,若,则的度数为 .
9.如图,点P为外一点,PA为的切线,A为切点,PO交于点B,,,则线段BP的长为 .
10.如图,射线AB与⊙O相切于点B,经过圆心O的射线AC与⊙O相交于点D、C,连接BC,若∠A=40°,则∠ACB= .
11.如图,是的直径,,点在上(点不与、重合),过点作的切线交的延长线于点,连接.若,则的长度是 (结果保留)
三、计算题
12.如图1,一个圆球放置在V型架中.图2是它的平面示意图,CA、CB都是⊙O的切线,切点分别是A、B,如果⊙O的半径为cm,且AB=6cm,求∠ACB.
13.如图,正六边形是半径为1的的内接六边形,连接并延长到点,过点,交的延长线于点.
(1)是___________(填“直角”“等腰”或“等边”)三角形;
(2)当___________时,直线与相切,此时通过计算比较线段和劣弧长度哪个更长;(参考数据:取3)
(3)已知是上的动点(点不与点A,重合).
①连接,,求的度数;
②已知,过点作的切线,当切线与直线交于点时,请直接写出长的最小值.
14.在一次数学建模活动课上,吴老师制作了一张简易的海域安全监测平面图,在图中标明了三个监测点的位置坐标,,,由三个监测点确定的圆形区域是安全警戒区域.
(1)某天海面上出现可疑船只C,在监测点A测得C位于南偏东,同时在监测点O测得C位于南偏东,求监测点O到C船的距离.(结果精确到,参考数据:,,,)
(2)当可疑船只C由(1)中位置向正北方向航行时,是否会闯入安全警戒区域?请通过计算作答.
四、解答题
15.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
五、作图题
16.下列说法正确吗 若不正确,请画图说明.
(1)垂直于圆的半径的直线一定是这个圆的切线.
(2)过圆的半径的外端的直线一定是这个圆的切线.
六、综合题
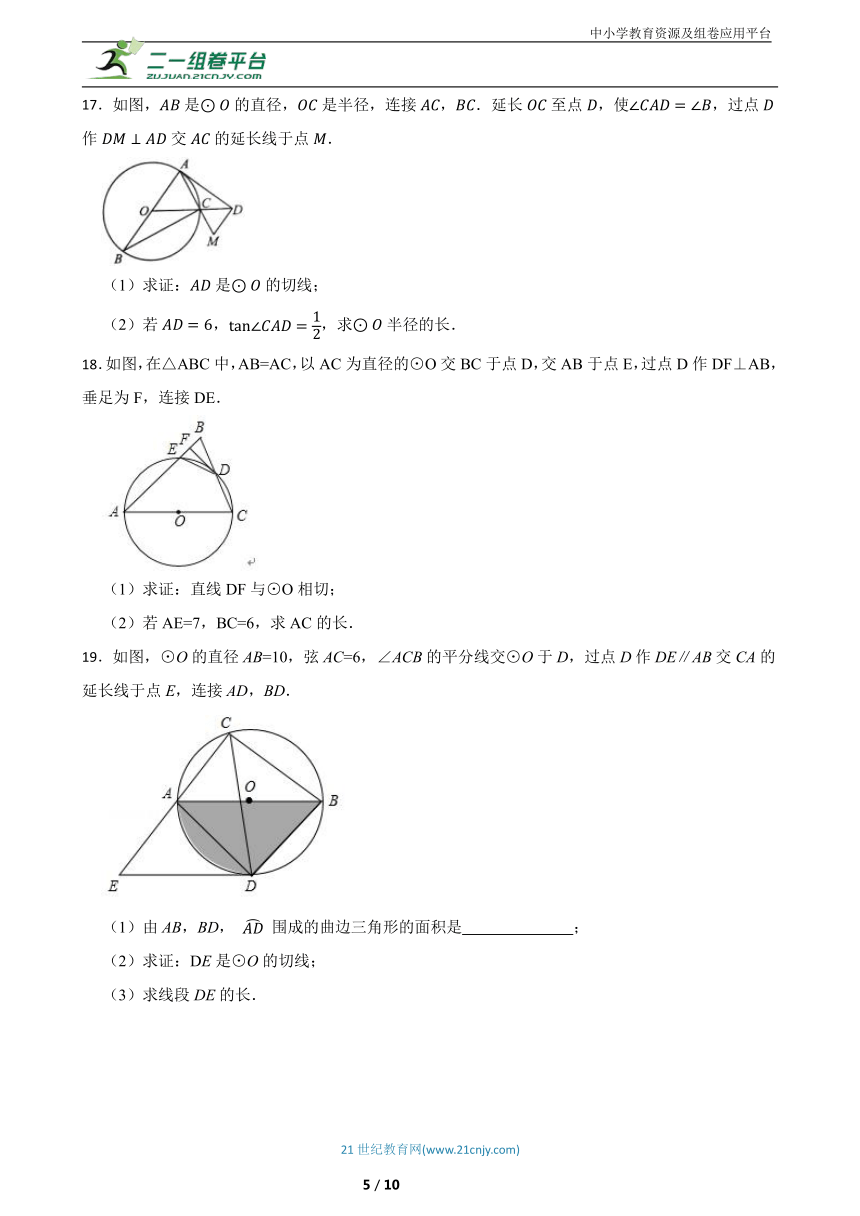
17.如图,是的直径,是半径,连接,.延长至点,使,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求半径的长.
18.如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
19.如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD, 围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
答案解析部分
1.【答案】B
【知识点】圆周角定理;切线的性质
2.【答案】D
【知识点】直线与圆的位置关系
3.【答案】D
【知识点】圆周角定理;切线的性质
4.【答案】A
【知识点】圆周角定理;切线的性质
5.【答案】A
【知识点】切线的性质;相似三角形的判定与性质
6.【答案】
【知识点】切线的性质;弧长的计算
7.【答案】7
【知识点】勾股定理;切线的性质
8.【答案】
【知识点】圆周角定理;切线的性质
9.【答案】3
【知识点】含30°角的直角三角形;切线的性质
10.【答案】25
【知识点】三角形的外角性质;切线的性质
11.【答案】
【知识点】三角形内角和定理;切线的性质;弧长的计算
12.【答案】解:如图,连接OC交AB于点D∵CA、CB分别是⊙O的切线∴CA=CB,OC平分∠ACB∴OC⊥AB∵AB=6∴BD=3在Rt△OBD中∵OB=∴sin∠BOD=∴∠BOD=60°∵B是切点∴OB⊥BC∴∠OCB=30°∴∠ACB=60°.
【知识点】切线的性质;解直角三角形
13.【答案】(1)等边
(2)
(3)①或,②
【知识点】圆周角定理;切线的性质;圆内接正多边形;解直角三角形
14.【答案】(1)
(2)不会
【知识点】矩形的判定与性质;直线与圆的位置关系;相似三角形的判定与性质;解直角三角形的实际应用﹣方向角问题
15.【答案】相切
【知识点】直线与圆的位置关系
16.【答案】(1)解:不正确,反例如下图:
直线l垂直于的半径OA,但直线l不是的切线;
(2)解:不正确,反例如下图:
直线l'过的半径OB外端点B,但直线l'不是的切线.
【知识点】切线的判定
17.【答案】(1)证明:∵是的直径
∴
∴
∵
∴
∴,
∴
∴是的切线;
(2)解:∵,
∴
∵
∴
∵,
∴
∴,
∵
∴
∴,
在中,,即
∴
∴半径长为.
【知识点】切线的判定;解直角三角形的其他实际应用
18.【答案】(1)证明:如图,
连接OD.
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴,
∵OD∥AB,AO=CO,
∴BD=CD=BC=3,
又∵AE=7,
∴,
∴BE=2,
∴AC=AB=AE+BE=7+2=9.
【知识点】切线的判定;相似三角形的判定与性质
19.【答案】(1)
(2)证明:由(1)知∠AOD=90°,即OD⊥AB.
∵DE∥AB,∴OD⊥DE,
∴DE是⊙O的切线;
(3)解:∵AB=10、AC=6,∴BC= =8. 过点A作AF⊥DE于点F,
则四边形AODF是正方形,∴AF=OD=FD=5,∴∠EAF=90°﹣∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴ ,即 , ∴EF= ,
∴DE=DF+EF= +5= .
【知识点】勾股定理;切线的判定;锐角三角函数的定义
21世纪教育网(www.21cnjy.com)
1 / 10
2.1直线和圆的位置关系
一、单选题
1.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )
A.55° B.70° C.110° D.125°
2.已知的半径为,若直线与圆心的距离为,则直线l与的位置关系是( )
A.相离 B.相切 C.相交或相离 D.相交
3.如图,点 为 外一点,过点 作 的切线 ,记切点为 ,点 为 上一点,连接 .若,则 等于( )
A. B. C. D.
4.如图、是的两条弦,,过点的切线与的延长线交于点,则的度数等于( )
A. B. C. D.
5.如图,在 中, , , ,以 为直径作圆与斜边交于点 ,则 的长为( )
A. B. C. D.
二、填空题
6.中国高铁已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线即圆弧,高铁列车在转弯时的曲线起点为,曲线终点为,过点,的两条切线相交于点,列车在从到行驶的过程中转角为.若圆曲线的半径,则这段圆曲线弧的长为 .(结果保留)
7.如图,P是⊙O外一点,PA与⊙O相切于点A,若PO=25cm,PA=24cm,则⊙O的半径为 cm.
8.如图,点P为圆外一点,过点P作的切线、,A,B为切点.点C为上一点,若,则的度数为 .
9.如图,点P为外一点,PA为的切线,A为切点,PO交于点B,,,则线段BP的长为 .
10.如图,射线AB与⊙O相切于点B,经过圆心O的射线AC与⊙O相交于点D、C,连接BC,若∠A=40°,则∠ACB= .
11.如图,是的直径,,点在上(点不与、重合),过点作的切线交的延长线于点,连接.若,则的长度是 (结果保留)
三、计算题
12.如图1,一个圆球放置在V型架中.图2是它的平面示意图,CA、CB都是⊙O的切线,切点分别是A、B,如果⊙O的半径为cm,且AB=6cm,求∠ACB.
13.如图,正六边形是半径为1的的内接六边形,连接并延长到点,过点,交的延长线于点.
(1)是___________(填“直角”“等腰”或“等边”)三角形;
(2)当___________时,直线与相切,此时通过计算比较线段和劣弧长度哪个更长;(参考数据:取3)
(3)已知是上的动点(点不与点A,重合).
①连接,,求的度数;
②已知,过点作的切线,当切线与直线交于点时,请直接写出长的最小值.
14.在一次数学建模活动课上,吴老师制作了一张简易的海域安全监测平面图,在图中标明了三个监测点的位置坐标,,,由三个监测点确定的圆形区域是安全警戒区域.
(1)某天海面上出现可疑船只C,在监测点A测得C位于南偏东,同时在监测点O测得C位于南偏东,求监测点O到C船的距离.(结果精确到,参考数据:,,,)
(2)当可疑船只C由(1)中位置向正北方向航行时,是否会闯入安全警戒区域?请通过计算作答.
四、解答题
15.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
五、作图题
16.下列说法正确吗 若不正确,请画图说明.
(1)垂直于圆的半径的直线一定是这个圆的切线.
(2)过圆的半径的外端的直线一定是这个圆的切线.
六、综合题
17.如图,是的直径,是半径,连接,.延长至点,使,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求半径的长.
18.如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
19.如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD, 围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
答案解析部分
1.【答案】B
【知识点】圆周角定理;切线的性质
2.【答案】D
【知识点】直线与圆的位置关系
3.【答案】D
【知识点】圆周角定理;切线的性质
4.【答案】A
【知识点】圆周角定理;切线的性质
5.【答案】A
【知识点】切线的性质;相似三角形的判定与性质
6.【答案】
【知识点】切线的性质;弧长的计算
7.【答案】7
【知识点】勾股定理;切线的性质
8.【答案】
【知识点】圆周角定理;切线的性质
9.【答案】3
【知识点】含30°角的直角三角形;切线的性质
10.【答案】25
【知识点】三角形的外角性质;切线的性质
11.【答案】
【知识点】三角形内角和定理;切线的性质;弧长的计算
12.【答案】解:如图,连接OC交AB于点D∵CA、CB分别是⊙O的切线∴CA=CB,OC平分∠ACB∴OC⊥AB∵AB=6∴BD=3在Rt△OBD中∵OB=∴sin∠BOD=∴∠BOD=60°∵B是切点∴OB⊥BC∴∠OCB=30°∴∠ACB=60°.
【知识点】切线的性质;解直角三角形
13.【答案】(1)等边
(2)
(3)①或,②
【知识点】圆周角定理;切线的性质;圆内接正多边形;解直角三角形
14.【答案】(1)
(2)不会
【知识点】矩形的判定与性质;直线与圆的位置关系;相似三角形的判定与性质;解直角三角形的实际应用﹣方向角问题
15.【答案】相切
【知识点】直线与圆的位置关系
16.【答案】(1)解:不正确,反例如下图:
直线l垂直于的半径OA,但直线l不是的切线;
(2)解:不正确,反例如下图:
直线l'过的半径OB外端点B,但直线l'不是的切线.
【知识点】切线的判定
17.【答案】(1)证明:∵是的直径
∴
∴
∵
∴
∴,
∴
∴是的切线;
(2)解:∵,
∴
∵
∴
∵,
∴
∴,
∵
∴
∴,
在中,,即
∴
∴半径长为.
【知识点】切线的判定;解直角三角形的其他实际应用
18.【答案】(1)证明:如图,
连接OD.
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴,
∵OD∥AB,AO=CO,
∴BD=CD=BC=3,
又∵AE=7,
∴,
∴BE=2,
∴AC=AB=AE+BE=7+2=9.
【知识点】切线的判定;相似三角形的判定与性质
19.【答案】(1)
(2)证明:由(1)知∠AOD=90°,即OD⊥AB.
∵DE∥AB,∴OD⊥DE,
∴DE是⊙O的切线;
(3)解:∵AB=10、AC=6,∴BC= =8. 过点A作AF⊥DE于点F,
则四边形AODF是正方形,∴AF=OD=FD=5,∴∠EAF=90°﹣∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴ ,即 , ∴EF= ,
∴DE=DF+EF= +5= .
【知识点】勾股定理;切线的判定;锐角三角函数的定义
21世纪教育网(www.21cnjy.com)
1 / 10
