第二章直线和圆的位置关系综合题(含答案)
文档属性
| 名称 | 第二章直线和圆的位置关系综合题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 474.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章直线和圆的位置关系综合题
一、填空题
1.如果我们把太阳看作一个圆,把地平线看作一条直线,太阳在升起离开地平线后,太阳和地平线的位置关系是 .
2.点为外一点,直线与的两个公共点为、,过点作的切线,点为切点,连接.若,则为 .
3.如图, 为的直径, 为的切线,,则的度数为 .
4.如图,已知中,,,内切圆半径为,则图中阴影部分面积是 .
5.如图, , 分别与⊙O相切于 、 两点,点 为⊙O上一点,连接 、 ,若 ,则 的度数为 .
6.如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为 ,则△ABC的周长为 .
二、单选题
7.下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )
A.1个 B.2个 C.3个 D.0个
8.已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
9.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=55°,则∠COD的大小为( )
A.70° B.60° C.55° D.35°
10.如图,以为直径的上有一点C,过点C作的切线,过点O作,若,,则的长为( )
A. B. C.2 D.4
11.已知的半径,设圆心O到一条直线的距离为d,圆上到这条直线的距离为2的点的个数为m,给出下列命题:
①若,则;②若,则;③若,则;④若,则;⑤若,则.
其中正确命题的个数是( )
A.1 B.2 C.3 D.5
12.在Rt△ABC中,∠C=90°,AC=4,BC=3,则△ABC的内切圆半径为( )
A.5 B.2.5 C.1 D.0.5
13.若,,则以点O为圆心,为半径的圆与直线的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
14.如图,过点作的切线,,切点分别是,,连接.过上一点作的切线,交,于点,.若,的周长为4,则的长为( )
A.2 B. C.4 D.
15.如图,在 中, ,点 在 上,以点 为圆心, 为半径作 ,点 恰好在 上, 是 的切线,则 的度数是( )
A.35° B.30° C.25° D.20°
16.如图,在边长为1的菱形中,,动点E在边上(与点A、B均不重合),点F在对角线上,与相交于点G,连接,若,则下列结论错误的是( )
A. B.
C. D.的最小值为
三、解答题
17.如图,是的外接圆,,,P是上的一动点.
(1)当的度数为多少时,;
(2)若以动点P为切点的切线为,那么当的度数为多少时,切线与一边平行?
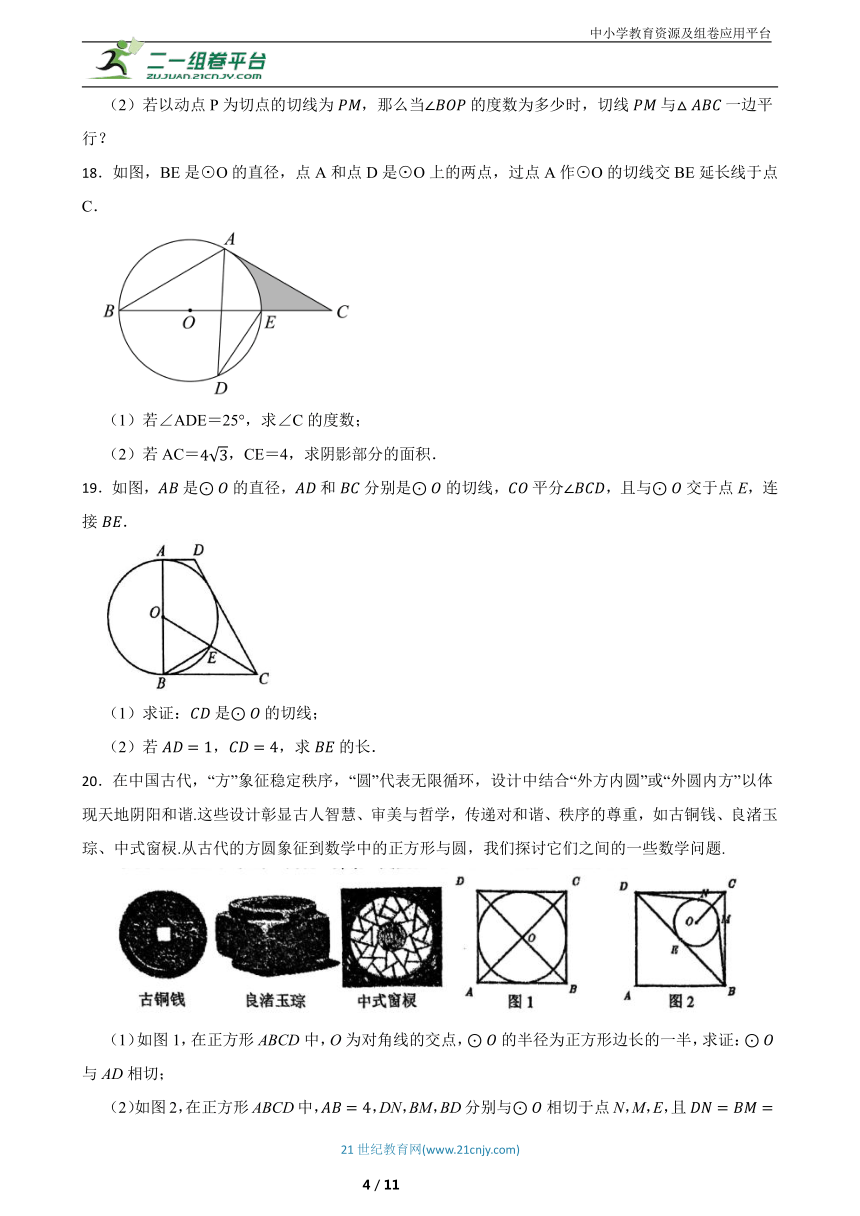
18.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=,CE=4,求阴影部分的面积.
19.如图,是的直径,和分别是的切线,平分,且与交于点E,连接.
(1)求证:是的切线;
(2)若,,求的长.
20.在中国古代,“方”象征稳定秩序,“圆”代表无限循环,设计中结合“外方内圆”或“外圆内方”以体现天地阴阳和谐.这些设计彰显古人智慧、审美与哲学,传递对和谐、秩序的尊重,如古铜钱、良渚玉琮、中式窗棂.从古代的方圆象征到数学中的正方形与圆,我们探讨它们之间的一些数学问题.
(1)如图1,在正方形ABCD中,O为对角线的交点,的半径为正方形边长的一半,求证:与AD相切;
(2)如图2,在正方形ABCD中,,DN,BM,BD分别与相切于点N,M,E,且,,求的半径;
(3)如图3,半径为1的在边长为4的正方形ABCD内任意移动,在其任意移动的过程中,所移动过的最大区域面积为 。
四、计算题
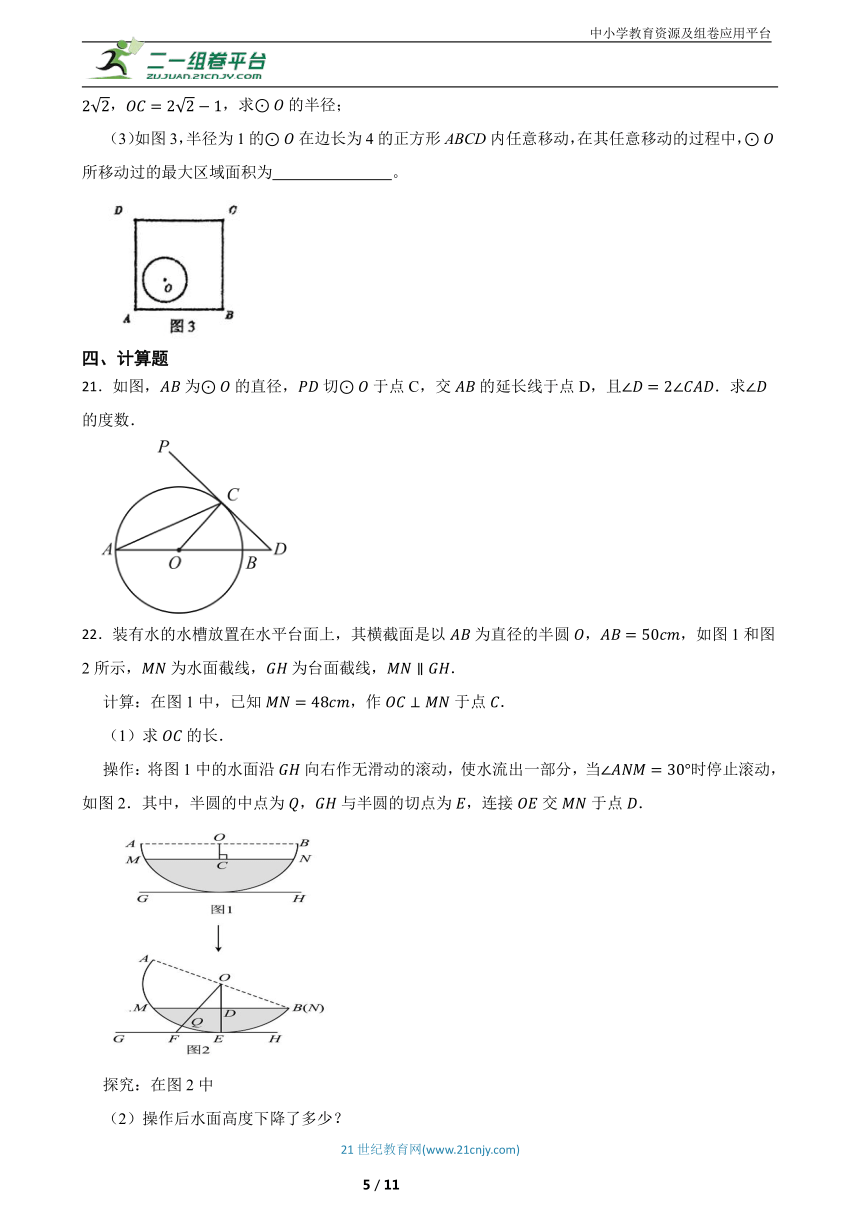
21.如图,为的直径,切于点C,交的延长线于点D,且.求的度数.
22.装有水的水槽放置在水平台面上,其横截面是以为直径的半圆,,如图1和图2所示,为水面截线,为台面截线,.
计算:在图1中,已知,作于点.
(1)求的长.
操作:将图1中的水面沿向右作无滑动的滚动,使水流出一部分,当时停止滚动,如图2.其中,半圆的中点为,与半圆的切点为,连接交于点.
探究:在图2中
(2)操作后水面高度下降了多少?
(3)连接OQ并延长交GH于点F,求线段与的长度,并比较大小.
23.如图1,在中,,,,点O在边AB上,且,以点O为圆心,2为半径在AB的上方作半圆O,交AB于点D,E,交AC于点P.将半圆O沿AB向右平移,设点D平移的距离为.
(1)在图1中,劣弧的长为________;
(2)当半圆O平移到与边AC相切时,如图2所示.
①求x的值;
②已知M,N分别是边BC与上的动点,连接MN,求MN的最小值和最大值之和;
(3)在半圆O沿边AB向右平移的过程中,当半圆O与的重叠部分是半圆O时,直接写出x的取值范围.
答案解析部分
1.【答案】相离
【知识点】直线与圆的位置关系
2.【答案】60°或30°
【知识点】等边三角形的判定与性质;圆周角定理;切线的性质
3.【答案】
【知识点】圆周角定理;切线的性质
4.【答案】
【知识点】三角形内角和定理;三角形的内切圆与内心;扇形面积的计算
5.【答案】
【知识点】多边形内角与外角;圆周角定理;切线的性质
6.【答案】25
【知识点】矩形的判定与性质;切线的性质;相似三角形的判定与性质;切线长定理
7.【答案】D
【知识点】垂径定理;圆心角、弧、弦的关系;确定圆的条件;切线的判定
8.【答案】C
【知识点】直线与圆的位置关系
9.【答案】A
【知识点】圆周角定理;切线的性质
10.【答案】D
【知识点】含30°角的直角三角形;勾股定理;圆周角定理;切线的性质
11.【答案】C
【知识点】直线与圆的位置关系;真命题与假命题
12.【答案】C
【知识点】三角形的内切圆与内心
13.【答案】C
【知识点】直线与圆的位置关系
14.【答案】B
【知识点】勾股定理;切线的性质
15.【答案】C
【知识点】三角形内角和定理;三角形的外角性质;切线的性质
16.【答案】D
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;三角形的内切圆与内心;相似三角形的判定与性质
17.【答案】(1)
(2)或或
【知识点】三角形内角和定理;垂径定理;圆周角定理;切线的性质
18.【答案】(1)∠C=40°;
(2)阴影部分的面积为.
【知识点】勾股定理;圆周角定理;切线的性质;扇形面积的计算
19.【答案】(1)证明:过点O作于F
∵是的切线,
∴于B,
又∵平分,
∴
是的半径
∴也是的半径
∴是的切线.
(2)方法一:
由(1)得是的切线,切点为F,
∵和分别是的切线,
∴
∵和分别是的切线,
∴
过点D作于H,即
∴四边形是矩形,
,
在中,
,
,.
,
∴.
∴
∴,
又
∴是等边三角形,
∴.
方法二:
由(1)得是的切线,切点为F,
和分别是的切线,
∴
.
∵和分别是的切线,
∴
∴
∴
∴.
连接
∵是的切线,切点为F,
和分别是的切线,
∴,
∴
∴.
设的半径为r
,
∴
解得.
在中,
∵
∴
∴点E是中点,
∴
【知识点】等边三角形的判定与性质;勾股定理;矩形的判定与性质;切线的判定与性质
20.【答案】(1)证明:过作于E,如图:
∵四边形ABCD为正方形,
∴,
∴OE平分AD,即.
∴,即OE等于的半径
∴与AD相切.
(2)解:连接OE,如图:
∵BD与切于点E
∴
由切线长定理可得:,
∵
∴
∴OE垂直平分BD.
在正方形ABCD中,∵,
∴,点C也在BD的垂直平分线上
∴C,O,E共线,
∴,
∵
∴
∴的半径为1.
(3)解:
【知识点】正方形的性质;切线的判定与性质
21.【答案】
【知识点】等腰三角形的性质;切线的性质
22.【答案】(1);(2);(3),,.
【知识点】垂径定理;切线的性质;解直角三角形
23.【答案】(1)
(2)①;②MN的最小值和最大值之和为
(3)半圆O与的重叠部分是半圆O时,x的取值范围是
【知识点】含30°角的直角三角形;勾股定理;切线的性质;弧长的计算
21世纪教育网(www.21cnjy.com)
2 / 11
第二章直线和圆的位置关系综合题
一、填空题
1.如果我们把太阳看作一个圆,把地平线看作一条直线,太阳在升起离开地平线后,太阳和地平线的位置关系是 .
2.点为外一点,直线与的两个公共点为、,过点作的切线,点为切点,连接.若,则为 .
3.如图, 为的直径, 为的切线,,则的度数为 .
4.如图,已知中,,,内切圆半径为,则图中阴影部分面积是 .
5.如图, , 分别与⊙O相切于 、 两点,点 为⊙O上一点,连接 、 ,若 ,则 的度数为 .
6.如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为 ,则△ABC的周长为 .
二、单选题
7.下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )
A.1个 B.2个 C.3个 D.0个
8.已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
9.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=55°,则∠COD的大小为( )
A.70° B.60° C.55° D.35°
10.如图,以为直径的上有一点C,过点C作的切线,过点O作,若,,则的长为( )
A. B. C.2 D.4
11.已知的半径,设圆心O到一条直线的距离为d,圆上到这条直线的距离为2的点的个数为m,给出下列命题:
①若,则;②若,则;③若,则;④若,则;⑤若,则.
其中正确命题的个数是( )
A.1 B.2 C.3 D.5
12.在Rt△ABC中,∠C=90°,AC=4,BC=3,则△ABC的内切圆半径为( )
A.5 B.2.5 C.1 D.0.5
13.若,,则以点O为圆心,为半径的圆与直线的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
14.如图,过点作的切线,,切点分别是,,连接.过上一点作的切线,交,于点,.若,的周长为4,则的长为( )
A.2 B. C.4 D.
15.如图,在 中, ,点 在 上,以点 为圆心, 为半径作 ,点 恰好在 上, 是 的切线,则 的度数是( )
A.35° B.30° C.25° D.20°
16.如图,在边长为1的菱形中,,动点E在边上(与点A、B均不重合),点F在对角线上,与相交于点G,连接,若,则下列结论错误的是( )
A. B.
C. D.的最小值为
三、解答题
17.如图,是的外接圆,,,P是上的一动点.
(1)当的度数为多少时,;
(2)若以动点P为切点的切线为,那么当的度数为多少时,切线与一边平行?
18.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=,CE=4,求阴影部分的面积.
19.如图,是的直径,和分别是的切线,平分,且与交于点E,连接.
(1)求证:是的切线;
(2)若,,求的长.
20.在中国古代,“方”象征稳定秩序,“圆”代表无限循环,设计中结合“外方内圆”或“外圆内方”以体现天地阴阳和谐.这些设计彰显古人智慧、审美与哲学,传递对和谐、秩序的尊重,如古铜钱、良渚玉琮、中式窗棂.从古代的方圆象征到数学中的正方形与圆,我们探讨它们之间的一些数学问题.
(1)如图1,在正方形ABCD中,O为对角线的交点,的半径为正方形边长的一半,求证:与AD相切;
(2)如图2,在正方形ABCD中,,DN,BM,BD分别与相切于点N,M,E,且,,求的半径;
(3)如图3,半径为1的在边长为4的正方形ABCD内任意移动,在其任意移动的过程中,所移动过的最大区域面积为 。
四、计算题
21.如图,为的直径,切于点C,交的延长线于点D,且.求的度数.
22.装有水的水槽放置在水平台面上,其横截面是以为直径的半圆,,如图1和图2所示,为水面截线,为台面截线,.
计算:在图1中,已知,作于点.
(1)求的长.
操作:将图1中的水面沿向右作无滑动的滚动,使水流出一部分,当时停止滚动,如图2.其中,半圆的中点为,与半圆的切点为,连接交于点.
探究:在图2中
(2)操作后水面高度下降了多少?
(3)连接OQ并延长交GH于点F,求线段与的长度,并比较大小.
23.如图1,在中,,,,点O在边AB上,且,以点O为圆心,2为半径在AB的上方作半圆O,交AB于点D,E,交AC于点P.将半圆O沿AB向右平移,设点D平移的距离为.
(1)在图1中,劣弧的长为________;
(2)当半圆O平移到与边AC相切时,如图2所示.
①求x的值;
②已知M,N分别是边BC与上的动点,连接MN,求MN的最小值和最大值之和;
(3)在半圆O沿边AB向右平移的过程中,当半圆O与的重叠部分是半圆O时,直接写出x的取值范围.
答案解析部分
1.【答案】相离
【知识点】直线与圆的位置关系
2.【答案】60°或30°
【知识点】等边三角形的判定与性质;圆周角定理;切线的性质
3.【答案】
【知识点】圆周角定理;切线的性质
4.【答案】
【知识点】三角形内角和定理;三角形的内切圆与内心;扇形面积的计算
5.【答案】
【知识点】多边形内角与外角;圆周角定理;切线的性质
6.【答案】25
【知识点】矩形的判定与性质;切线的性质;相似三角形的判定与性质;切线长定理
7.【答案】D
【知识点】垂径定理;圆心角、弧、弦的关系;确定圆的条件;切线的判定
8.【答案】C
【知识点】直线与圆的位置关系
9.【答案】A
【知识点】圆周角定理;切线的性质
10.【答案】D
【知识点】含30°角的直角三角形;勾股定理;圆周角定理;切线的性质
11.【答案】C
【知识点】直线与圆的位置关系;真命题与假命题
12.【答案】C
【知识点】三角形的内切圆与内心
13.【答案】C
【知识点】直线与圆的位置关系
14.【答案】B
【知识点】勾股定理;切线的性质
15.【答案】C
【知识点】三角形内角和定理;三角形的外角性质;切线的性质
16.【答案】D
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;三角形的内切圆与内心;相似三角形的判定与性质
17.【答案】(1)
(2)或或
【知识点】三角形内角和定理;垂径定理;圆周角定理;切线的性质
18.【答案】(1)∠C=40°;
(2)阴影部分的面积为.
【知识点】勾股定理;圆周角定理;切线的性质;扇形面积的计算
19.【答案】(1)证明:过点O作于F
∵是的切线,
∴于B,
又∵平分,
∴
是的半径
∴也是的半径
∴是的切线.
(2)方法一:
由(1)得是的切线,切点为F,
∵和分别是的切线,
∴
∵和分别是的切线,
∴
过点D作于H,即
∴四边形是矩形,
,
在中,
,
,.
,
∴.
∴
∴,
又
∴是等边三角形,
∴.
方法二:
由(1)得是的切线,切点为F,
和分别是的切线,
∴
.
∵和分别是的切线,
∴
∴
∴
∴.
连接
∵是的切线,切点为F,
和分别是的切线,
∴,
∴
∴.
设的半径为r
,
∴
解得.
在中,
∵
∴
∴点E是中点,
∴
【知识点】等边三角形的判定与性质;勾股定理;矩形的判定与性质;切线的判定与性质
20.【答案】(1)证明:过作于E,如图:
∵四边形ABCD为正方形,
∴,
∴OE平分AD,即.
∴,即OE等于的半径
∴与AD相切.
(2)解:连接OE,如图:
∵BD与切于点E
∴
由切线长定理可得:,
∵
∴
∴OE垂直平分BD.
在正方形ABCD中,∵,
∴,点C也在BD的垂直平分线上
∴C,O,E共线,
∴,
∵
∴
∴的半径为1.
(3)解:
【知识点】正方形的性质;切线的判定与性质
21.【答案】
【知识点】等腰三角形的性质;切线的性质
22.【答案】(1);(2);(3),,.
【知识点】垂径定理;切线的性质;解直角三角形
23.【答案】(1)
(2)①;②MN的最小值和最大值之和为
(3)半圆O与的重叠部分是半圆O时,x的取值范围是
【知识点】含30°角的直角三角形;勾股定理;切线的性质;弧长的计算
21世纪教育网(www.21cnjy.com)
2 / 11
