3.4简单几何体的表面展开图 同步练习(含答案)
文档属性
| 名称 | 3.4简单几何体的表面展开图 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 184.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 14:18:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
3.4简单几何体的表面展开图
一、单选题
1.“争创全国文明典范城市,让文明成为长春人民的内在气质和城市的亮丽名片”.一个写有相关宣传标语的正方体的表面展开图如图所示,把展开图折叠成正方体后,“范”字对面的字是( )
A.文 B.明 C.城 D.市
2.底面半径为,高为的圆锥的侧面展开图的面积为( )
A. B. C. D.
3.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )
A. B. C. D.
4.若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是( )
A.90° B.120° C.150° D.180°
5.下列平面图形中,经过折叠不能围成正方体的是( )
A. B.
C. D.
6.如图,在有序号的方格中选出一个画出阴影,使它们与图中五个有阴影的正方形一起可以构成正方体表面的展开图,正确的选法是( )
A.只有② B.只有①④
C.只有①②④ D.①②③④都符合题意
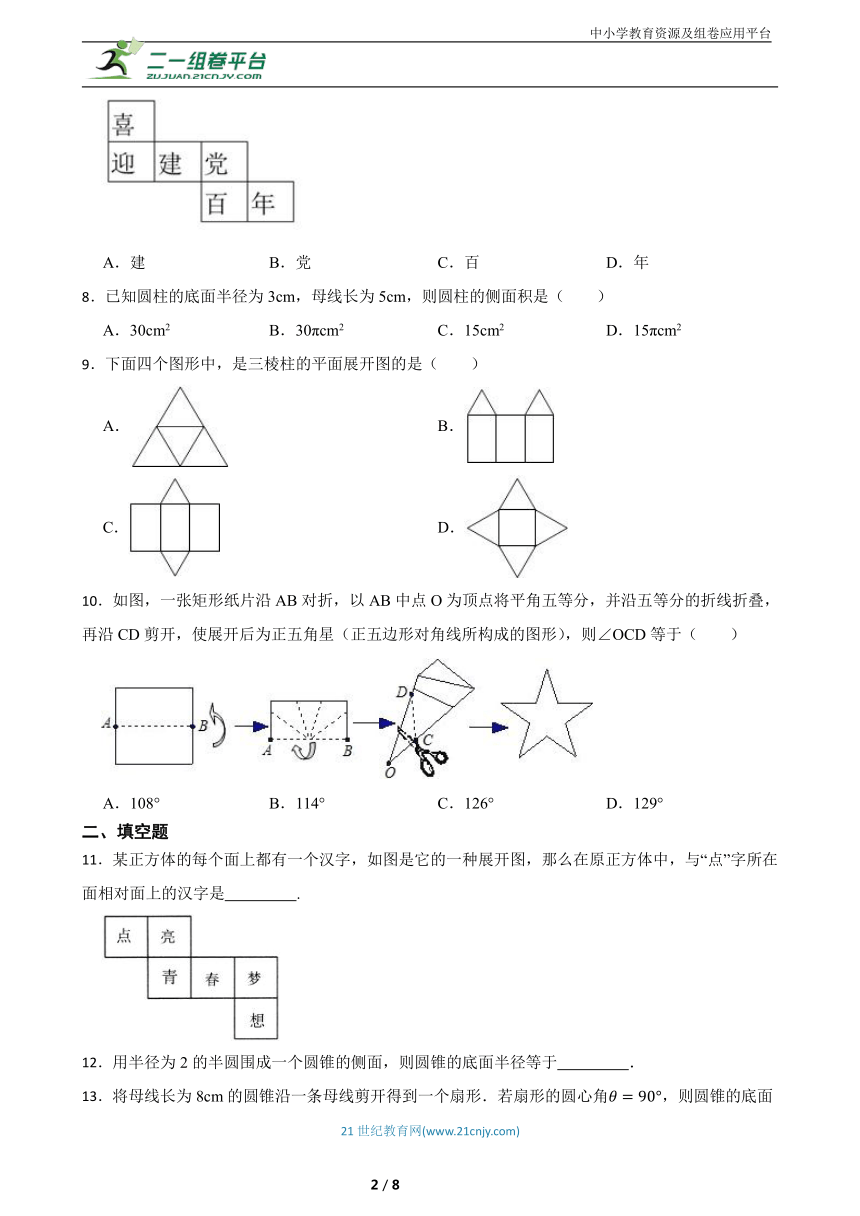
7.如图正方体的平面展开图可知,原正方体“喜”字所在面的对面的汉字是( )
A.建 B.党 C.百 D.年
8.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是( )
A.30cm2 B.30πcm2 C.15cm2 D.15πcm2
9.下面四个图形中,是三棱柱的平面展开图的是( )
A. B.
C. D.
10.如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )
A.108° B.114° C.126° D.129°
二、填空题
11.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对面上的汉字是 .
12.用半径为2的半圆围成一个圆锥的侧面,则圆锥的底面半径等于 .
13.将母线长为8cm的圆锥沿一条母线剪开得到一个扇形.若扇形的圆心角,则圆锥的底面圆半径r为 cm.
14.下列图形中,不能够折叠成正方体的有 (填序号)
15.如图所示,一圆柱高为8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是 cm.
16.如图所示,是长方形地面,长,宽,中间竖有一堵砖墙高.一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它至少要走 的路程.
三、计算题
17.已知:
(1)化简;
(2)若某圆锥的底面半径为,线母长为,且侧面积为,求的值.
18.如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,求x+y+z的值.
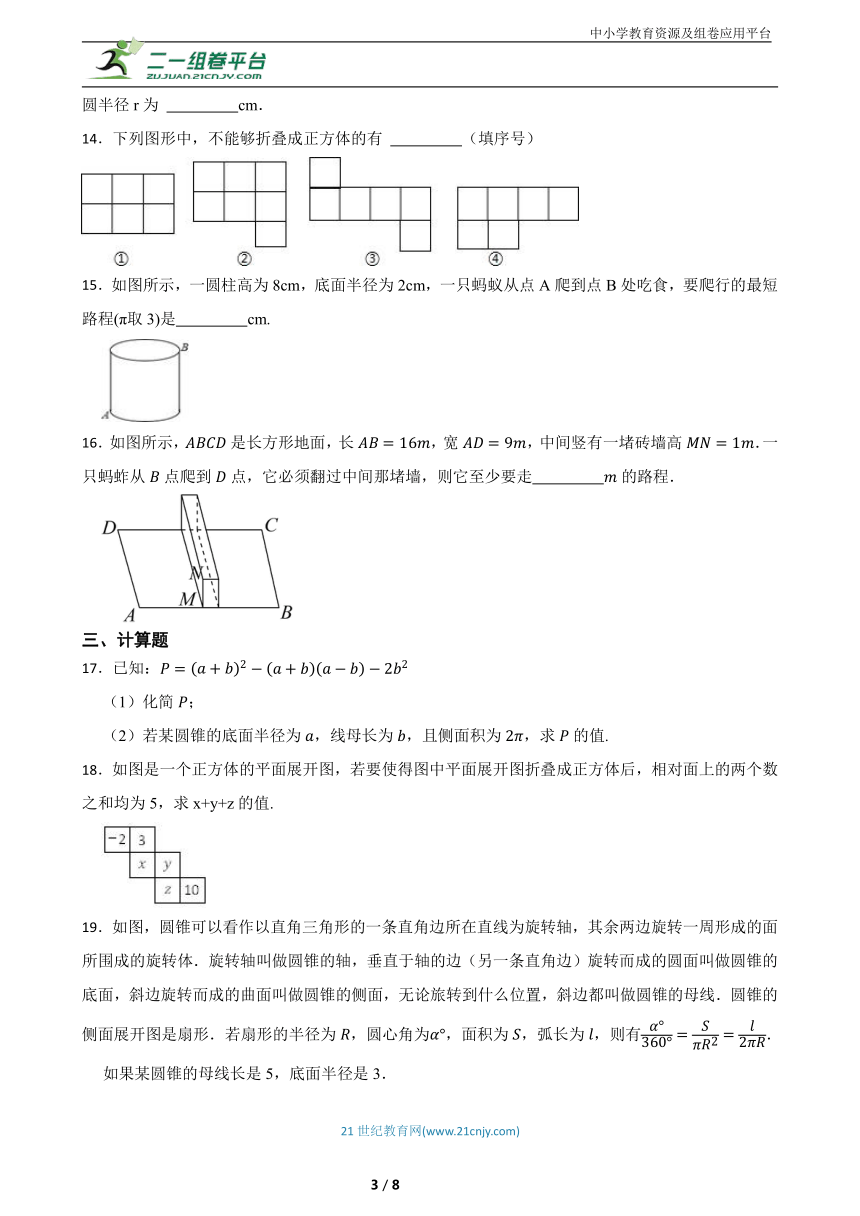
19.如图,圆锥可以看作以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体.旋转轴叫做圆锥的轴,垂直于轴的边(另一条直角边)旋转而成的圆面叫做圆锥的底面,斜边旋转而成的曲面叫做圆锥的侧面,无论旅转到什么位置,斜边都叫做圆锥的母线.圆锥的侧面展开图是扇形.若扇形的半径为,圆心角为,面积为,弧长为,则有.
如果某圆锥的母线长是5,底面半径是3.
(1)求该圆锥侧面展开图的面积;
(2)是圆锥的一条母线,过圆锥底面圆心作的垂线,垂足为,求绕圆锥的轴旋转一周所得曲面将圆锥分成两部分的体积比.
四、解答题
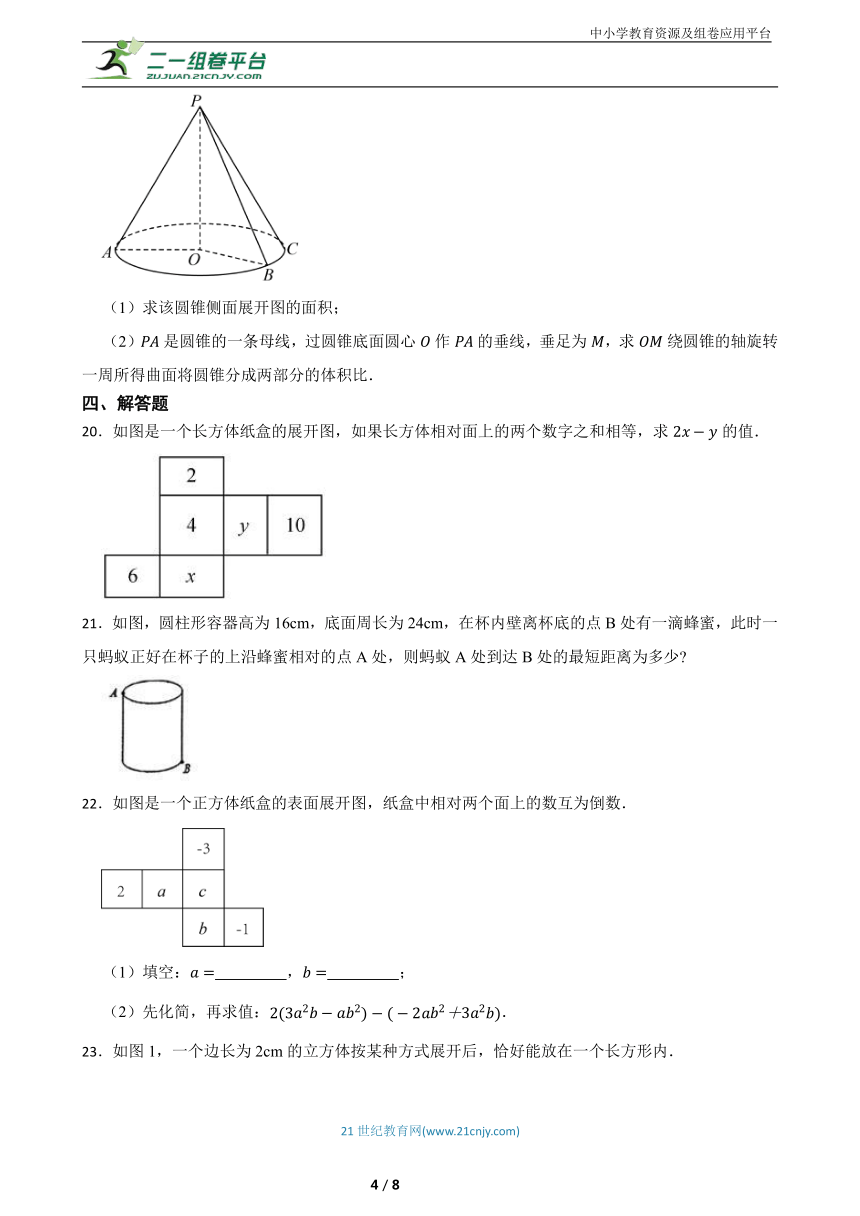
20.如图是一个长方体纸盒的展开图,如果长方体相对面上的两个数字之和相等,求的值.
21.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少
22.如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.
(1)填空: , ;
(2)先化简,再求值:.
23.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
答案解析部分
1.【答案】A
【知识点】几何体的展开图
2.【答案】A
【知识点】圆锥的计算
3.【答案】C
【知识点】圆锥的计算
4.【答案】D
【知识点】圆锥的计算
5.【答案】C
【知识点】几何体的展开图
6.【答案】A
【知识点】几何体的展开图
7.【答案】C
【知识点】几何体的展开图
8.【答案】B
【知识点】几何体的表面积;圆柱的计算
9.【答案】C
【知识点】几何体的展开图
10.【答案】C
【知识点】几何体的展开图;三角形内角和定理
11.【答案】春
【知识点】几何体的展开图
12.【答案】
【知识点】圆锥的计算
13.【答案】2
【知识点】弧长的计算;圆锥的计算
14.【答案】①②④
【知识点】几何体的展开图
15.【答案】10
【知识点】几何体的展开图;两点之间线段最短;勾股定理
16.【答案】
【知识点】几何体的展开图;两点之间线段最短;勾股定理;矩形的性质
17.【答案】(1)
(2)
【知识点】完全平方公式及运用;平方差公式及应用;圆锥的计算
18.【答案】解:由于正方体的平面展开图共有六个面,
其中面“z”与面“3”相对,面“y”与面“-2”相对,面“x”与面“10”相对,
则z+3=5,y+(-2)=5,x+10=5
解得z=2,y=7,x=-5
故x+y+z=4
【知识点】几何体的展开图
19.【答案】(1)
(2)上下两部分体积的比为
【知识点】勾股定理;扇形面积的计算;圆锥的计算
20.【答案】16
【知识点】几何体的展开图
21.【答案】解:如图所示,圆柱形玻璃容器,高16cm,底面周长为24cm,
∴在Rt△ABD中,BD=12,AD=16
∴AB2=DA2+DB2=122+162=202,解得:AB=20
∴蚂蚁A处到达B处的最短距离为20cm
【知识点】几何体的展开图;两点之间线段最短;勾股定理的应用
22.【答案】(1)-1;
(2)解:
∵
∴原式
【知识点】几何体的展开图;正方形的性质;利用整式的混合运算化简求值
23.【答案】(1)立方体的棱长为2cm,图1长方形的面积为4×2×3×2=48平方厘米。
(2)展开图:
(3)
【知识点】几何体的展开图;由三视图判断几何体
21世纪教育网(www.21cnjy.com)
8 / 8
3.4简单几何体的表面展开图
一、单选题
1.“争创全国文明典范城市,让文明成为长春人民的内在气质和城市的亮丽名片”.一个写有相关宣传标语的正方体的表面展开图如图所示,把展开图折叠成正方体后,“范”字对面的字是( )
A.文 B.明 C.城 D.市
2.底面半径为,高为的圆锥的侧面展开图的面积为( )
A. B. C. D.
3.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )
A. B. C. D.
4.若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是( )
A.90° B.120° C.150° D.180°
5.下列平面图形中,经过折叠不能围成正方体的是( )
A. B.
C. D.
6.如图,在有序号的方格中选出一个画出阴影,使它们与图中五个有阴影的正方形一起可以构成正方体表面的展开图,正确的选法是( )
A.只有② B.只有①④
C.只有①②④ D.①②③④都符合题意
7.如图正方体的平面展开图可知,原正方体“喜”字所在面的对面的汉字是( )
A.建 B.党 C.百 D.年
8.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是( )
A.30cm2 B.30πcm2 C.15cm2 D.15πcm2
9.下面四个图形中,是三棱柱的平面展开图的是( )
A. B.
C. D.
10.如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )
A.108° B.114° C.126° D.129°
二、填空题
11.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对面上的汉字是 .
12.用半径为2的半圆围成一个圆锥的侧面,则圆锥的底面半径等于 .
13.将母线长为8cm的圆锥沿一条母线剪开得到一个扇形.若扇形的圆心角,则圆锥的底面圆半径r为 cm.
14.下列图形中,不能够折叠成正方体的有 (填序号)
15.如图所示,一圆柱高为8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是 cm.
16.如图所示,是长方形地面,长,宽,中间竖有一堵砖墙高.一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它至少要走 的路程.
三、计算题
17.已知:
(1)化简;
(2)若某圆锥的底面半径为,线母长为,且侧面积为,求的值.
18.如图是一个正方体的平面展开图,若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和均为5,求x+y+z的值.
19.如图,圆锥可以看作以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体.旋转轴叫做圆锥的轴,垂直于轴的边(另一条直角边)旋转而成的圆面叫做圆锥的底面,斜边旋转而成的曲面叫做圆锥的侧面,无论旅转到什么位置,斜边都叫做圆锥的母线.圆锥的侧面展开图是扇形.若扇形的半径为,圆心角为,面积为,弧长为,则有.
如果某圆锥的母线长是5,底面半径是3.
(1)求该圆锥侧面展开图的面积;
(2)是圆锥的一条母线,过圆锥底面圆心作的垂线,垂足为,求绕圆锥的轴旋转一周所得曲面将圆锥分成两部分的体积比.
四、解答题
20.如图是一个长方体纸盒的展开图,如果长方体相对面上的两个数字之和相等,求的值.
21.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少
22.如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.
(1)填空: , ;
(2)先化简,再求值:.
23.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
答案解析部分
1.【答案】A
【知识点】几何体的展开图
2.【答案】A
【知识点】圆锥的计算
3.【答案】C
【知识点】圆锥的计算
4.【答案】D
【知识点】圆锥的计算
5.【答案】C
【知识点】几何体的展开图
6.【答案】A
【知识点】几何体的展开图
7.【答案】C
【知识点】几何体的展开图
8.【答案】B
【知识点】几何体的表面积;圆柱的计算
9.【答案】C
【知识点】几何体的展开图
10.【答案】C
【知识点】几何体的展开图;三角形内角和定理
11.【答案】春
【知识点】几何体的展开图
12.【答案】
【知识点】圆锥的计算
13.【答案】2
【知识点】弧长的计算;圆锥的计算
14.【答案】①②④
【知识点】几何体的展开图
15.【答案】10
【知识点】几何体的展开图;两点之间线段最短;勾股定理
16.【答案】
【知识点】几何体的展开图;两点之间线段最短;勾股定理;矩形的性质
17.【答案】(1)
(2)
【知识点】完全平方公式及运用;平方差公式及应用;圆锥的计算
18.【答案】解:由于正方体的平面展开图共有六个面,
其中面“z”与面“3”相对,面“y”与面“-2”相对,面“x”与面“10”相对,
则z+3=5,y+(-2)=5,x+10=5
解得z=2,y=7,x=-5
故x+y+z=4
【知识点】几何体的展开图
19.【答案】(1)
(2)上下两部分体积的比为
【知识点】勾股定理;扇形面积的计算;圆锥的计算
20.【答案】16
【知识点】几何体的展开图
21.【答案】解:如图所示,圆柱形玻璃容器,高16cm,底面周长为24cm,
∴在Rt△ABD中,BD=12,AD=16
∴AB2=DA2+DB2=122+162=202,解得:AB=20
∴蚂蚁A处到达B处的最短距离为20cm
【知识点】几何体的展开图;两点之间线段最短;勾股定理的应用
22.【答案】(1)-1;
(2)解:
∵
∴原式
【知识点】几何体的展开图;正方形的性质;利用整式的混合运算化简求值
23.【答案】(1)立方体的棱长为2cm,图1长方形的面积为4×2×3×2=48平方厘米。
(2)展开图:
(3)
【知识点】几何体的展开图;由三视图判断几何体
21世纪教育网(www.21cnjy.com)
8 / 8
