第一章二次函数与实际问题题型2024--2025学年浙教版九年级数学上册(含答案)
文档属性
| 名称 | 第一章二次函数与实际问题题型2024--2025学年浙教版九年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 17:28:25 | ||
图片预览




文档简介
二次函数与实际问题题型
一、实际生活中的应用
1.某游乐园要建造一个直径为26m的圆形喷水池,计划在喷水池的周边安装一圈喷水头,使喷出的水柱距池中心5m处达到最高,高度为8m.
(1)以水平方向为x轴,喷水池中心为原点建立直角坐标系,求在y轴右侧抛物线的函数表达式;
(2)要在喷水池的中心设计一个装饰物,使各方向喷出的水柱在此汇合,求这个装饰物的设计高度.
2.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为米.
(1)若苗圃园的面积为72平方米,求;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
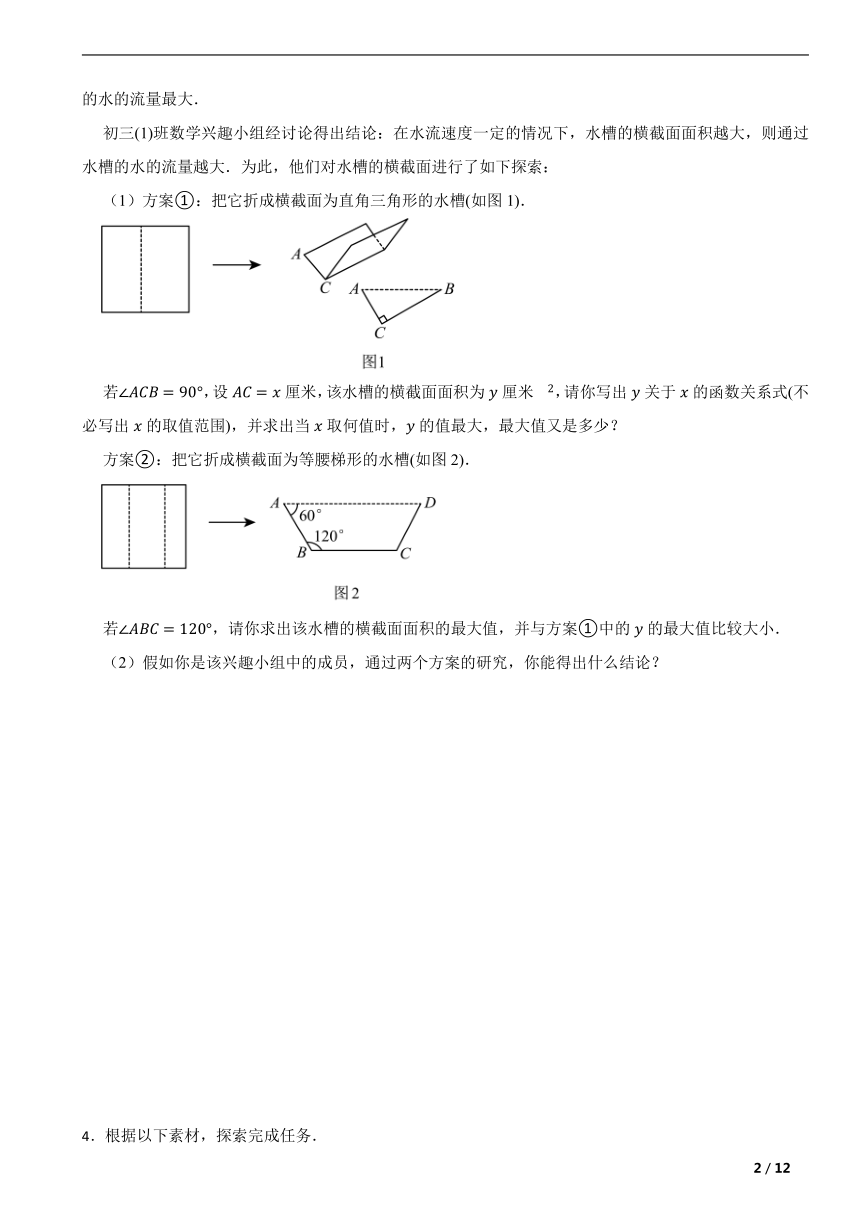
3.课题研究:现有边长为120厘米的正方形铁皮,准备将它设计并制成一个开口的水槽,使水槽能通过的水的流量最大.
初三(1)班数学兴趣小组经讨论得出结论:在水流速度一定的情况下,水槽的横截面面积越大,则通过水槽的水的流量越大.为此,他们对水槽的横截面进行了如下探索:
(1)方案①:把它折成横截面为直角三角形的水槽(如图1).
若,设厘米,该水槽的横截面面积为厘米,请你写出关于的函数关系式(不必写出的取值范围),并求出当取何值时,的值最大,最大值又是多少?
方案②:把它折成横截面为等腰梯形的水槽(如图2).
若,请你求出该水槽的横截面面积的最大值,并与方案①中的的最大值比较大小.
(2)假如你是该兴趣小组中的成员,通过两个方案的研究,你能得出什么结论?
4.根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽40m,拱顶离水面8m.据调查,该河段水位在此基础上再涨2.1m达到最高.
素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
(1)任务1:确定桥拱形状:
在图2建立合适的直角坐标系,求抛物线的函数表达式.
(2)任务2:探究悬挂范围:
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
(3)任务3:拟定设计方案:
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
二、最值求法
5.合肥某商场购进一批新型网红玩具.已知这种玩具进价为17元/件,且该玩具的月销售量y(件)与销售单价x(元)之间满足一次函数关系,下表是月销售量与销售单价的几组对应关系:
销售单价x/元 20 25 30 35
月销售量y/件 3300 2800 2300 1800
(1)求y关于x的函数关系式;
(2)当销售单价为多少元时,月销售利润最大,最大利润是多少?
6.如图是一块篱笆围成的矩形土地,并且由一条与边平行的篱笆分开,已知篱笆的总长为90米(厚度不计).设米,米.
(1)用含有的代数式表示.
(2)设矩形土地面积为平方米,当时,求的最大值.
7.有这样一个例题:有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为时,透光面积最大值约为.我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为,利用图3,解答下列问题:
(1)若为,求此时窗户的透光面积?
(2)与上一个例题比较,改变窗户形状后,若设的长度为,请问当x的值为多少时窗户透光面积最大?与例题相比透光的最大面积是否变大?通过计算说明.
三、有关分段函数
8.传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
四、限定自变量取值范围
9.某商场要经营一种新上市的文具,进价为20元/件,试营业阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)商场的营销部结合实际情况,决定该文具的销售单价不低于30元,且每天的销售量不得少于160件,那么该文具如何定价每天的最大销售利润最大,最大利润是多少.
10.大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨元(为非负整数),每个月的销售利润为元.
(1)求与的函数关系式,并直接写出自变量的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价为多少元时,每个月的利润恰好是1920元?
11.某服装厂生产品种服装,每件成本为71元,零售商到此服装厂一次性批发品牌服装件时,批发单价为元,与之间满足如图所示的函数关系,其中批发件数为10的正整数倍.
(1)当时,与的函数关系式为__________.
(2)某零售商到此服装厂一次性批发品牌服装200件,需要支付多少元?
(3)零售商到此服装厂一次性批发品牌服装件,服装厂的利润为元,问:为何值时,最大?最大值是多少?
12.根据背景素材,探索解决实际问题
乒乓球发球机的运动路线
素材一 如图1所示,乒乓球台规格是矩形,长为米,宽为米,球网高度为米某品牌.乒乓球发球机的出球口在桌面中线端点O处的正上方米处P.
素材二 如图2所示,假设每次发出的乒乓球都落在中线上,且球的运动路线是一条抛物线,且形状固定不变,在与P水平距离为1m的Q点正上方达到最高点,此时与桌面的高度为.并且乒乓球落在桌面的点M处,以O为原点,桌面中线所在直线为轴,建立平面直角坐标系.
素材三 如图3所示,若乒乓球落在桌面上弹起后,在与O点的水平距离为3米的位置达到最高点,设球达到最高时距离桌面的高度为h米.
问题解决
任务一 研究乒乓球飞行轨迹及落点 (1)求出发球机发球后到落在桌面前,乒乓球运动的抛物线关系式,并求出点M与O的水平距离.
任务二 击球点的确定 (2)当时,运动员小亮想把球沿直线擦网击打到O点,他能不能实现,若能实现,请求出击球点位置的高度,若不能实现,请说明理由.
任务三 运动员移动的距离 (3)当时,运动员小亮的球拍A离点O的水平距离为,位于桌面上方,离桌面,且运动员挥拍的过程中,球拍的击打路线近似于一条直线,球拍与桌面的夹角为,如图3所示.当球飞行的高度在至时,小亮可以获得最佳击球效果.小亮想要成功击中乒乓球,球拍需要先向前平移,设球拍向前平移的距离为n,则n的取值范围为 ;
参考答案
1.(1)解:∵抛物线的顶点坐标为(5,8),
∴设 y=a(x-5)2+8,
把(13,0)代入,得:0=a(13-5)2+8,
解得:a=-,
∴在 y 轴右侧抛物线的函数表达式为:y=- (x-5) 2+8.
(2)解:在 中,
当 时,
答: 这个装饰物的设计高度为 .
2.(1)的值为12
(2)这个苗圃园的面积有最大值和最小值,最大值为平方米,最小值为88平方米
3.(1)解:方案①将二次函数的解析式由一般式化为顶点式可得:,
当时,取得最大值,最大值为;
②如图所示,过点作于,于,则,
设,梯形的面积为,则,
又∵,
∴,,,
;
当,
∵,
;
(2)解:由(1)的结果大致可推断出折的边数越多,面积越大,因此折的边数无限多即折的图形为半圆时面积最大.
4.(1)解:如下图建立空间直角坐标系:
则顶点坐标为,则可设抛物线的解析式为:又抛物线经过点,则解得:则抛物线的解析式为:
(2)解:由题意知: 河段水位在此基础上再涨2.1m达到最高且 灯笼底部距离水面不小于1m ,灯笼长0.4m,则灯笼悬挂点的纵坐标:所以悬挂点的纵坐标最小值为,当时解得:所以悬挂点横坐标的取值范围为:
(3)解:从顶点处开始悬挂,因为,且相邻两盏灯笼悬挂点的水平间距均为1.6m,若顶点一侧悬挂灯笼时,则顶点一侧最多悬挂15盏灯笼,此时最左边悬挂点的横坐标为:共悬挂30盏灯笼.
5.(1)y=﹣100x+5300;(2)当销售单价为35元时,月销售利润最大,最大利润是32400元.
6.(1)
(2)当时,S取得最大值,
7.(1)
(2)当时,窗户透光面积最大,与例题相比透光的最大面积变大
8.(1)李明第10天生产的粽子数量为280只.(2)第13天的利润最大,最大利润是578元.
9.(1);(2)34;2240;
10.(1);自变量的取值范围为,且x为整数
(2)每件商品售价为33元时,每个月可获得最大利润,最大利润为1950元
(3)每件商品售价为32元时,每个月可获得的利润恰好为1920元
11.(1) (2)18000元 (3)或;3800
12.任务一:,点M与O的水平距离为;任务二:不能实现;任务三:.
1 / 1
一、实际生活中的应用
1.某游乐园要建造一个直径为26m的圆形喷水池,计划在喷水池的周边安装一圈喷水头,使喷出的水柱距池中心5m处达到最高,高度为8m.
(1)以水平方向为x轴,喷水池中心为原点建立直角坐标系,求在y轴右侧抛物线的函数表达式;
(2)要在喷水池的中心设计一个装饰物,使各方向喷出的水柱在此汇合,求这个装饰物的设计高度.
2.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为米.
(1)若苗圃园的面积为72平方米,求;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
3.课题研究:现有边长为120厘米的正方形铁皮,准备将它设计并制成一个开口的水槽,使水槽能通过的水的流量最大.
初三(1)班数学兴趣小组经讨论得出结论:在水流速度一定的情况下,水槽的横截面面积越大,则通过水槽的水的流量越大.为此,他们对水槽的横截面进行了如下探索:
(1)方案①:把它折成横截面为直角三角形的水槽(如图1).
若,设厘米,该水槽的横截面面积为厘米,请你写出关于的函数关系式(不必写出的取值范围),并求出当取何值时,的值最大,最大值又是多少?
方案②:把它折成横截面为等腰梯形的水槽(如图2).
若,请你求出该水槽的横截面面积的最大值,并与方案①中的的最大值比较大小.
(2)假如你是该兴趣小组中的成员,通过两个方案的研究,你能得出什么结论?
4.根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽40m,拱顶离水面8m.据调查,该河段水位在此基础上再涨2.1m达到最高.
素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
(1)任务1:确定桥拱形状:
在图2建立合适的直角坐标系,求抛物线的函数表达式.
(2)任务2:探究悬挂范围:
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
(3)任务3:拟定设计方案:
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
二、最值求法
5.合肥某商场购进一批新型网红玩具.已知这种玩具进价为17元/件,且该玩具的月销售量y(件)与销售单价x(元)之间满足一次函数关系,下表是月销售量与销售单价的几组对应关系:
销售单价x/元 20 25 30 35
月销售量y/件 3300 2800 2300 1800
(1)求y关于x的函数关系式;
(2)当销售单价为多少元时,月销售利润最大,最大利润是多少?
6.如图是一块篱笆围成的矩形土地,并且由一条与边平行的篱笆分开,已知篱笆的总长为90米(厚度不计).设米,米.
(1)用含有的代数式表示.
(2)设矩形土地面积为平方米,当时,求的最大值.
7.有这样一个例题:有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为时,透光面积最大值约为.我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为,利用图3,解答下列问题:
(1)若为,求此时窗户的透光面积?
(2)与上一个例题比较,改变窗户形状后,若设的长度为,请问当x的值为多少时窗户透光面积最大?与例题相比透光的最大面积是否变大?通过计算说明.
三、有关分段函数
8.传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
四、限定自变量取值范围
9.某商场要经营一种新上市的文具,进价为20元/件,试营业阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)商场的营销部结合实际情况,决定该文具的销售单价不低于30元,且每天的销售量不得少于160件,那么该文具如何定价每天的最大销售利润最大,最大利润是多少.
10.大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨元(为非负整数),每个月的销售利润为元.
(1)求与的函数关系式,并直接写出自变量的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价为多少元时,每个月的利润恰好是1920元?
11.某服装厂生产品种服装,每件成本为71元,零售商到此服装厂一次性批发品牌服装件时,批发单价为元,与之间满足如图所示的函数关系,其中批发件数为10的正整数倍.
(1)当时,与的函数关系式为__________.
(2)某零售商到此服装厂一次性批发品牌服装200件,需要支付多少元?
(3)零售商到此服装厂一次性批发品牌服装件,服装厂的利润为元,问:为何值时,最大?最大值是多少?
12.根据背景素材,探索解决实际问题
乒乓球发球机的运动路线
素材一 如图1所示,乒乓球台规格是矩形,长为米,宽为米,球网高度为米某品牌.乒乓球发球机的出球口在桌面中线端点O处的正上方米处P.
素材二 如图2所示,假设每次发出的乒乓球都落在中线上,且球的运动路线是一条抛物线,且形状固定不变,在与P水平距离为1m的Q点正上方达到最高点,此时与桌面的高度为.并且乒乓球落在桌面的点M处,以O为原点,桌面中线所在直线为轴,建立平面直角坐标系.
素材三 如图3所示,若乒乓球落在桌面上弹起后,在与O点的水平距离为3米的位置达到最高点,设球达到最高时距离桌面的高度为h米.
问题解决
任务一 研究乒乓球飞行轨迹及落点 (1)求出发球机发球后到落在桌面前,乒乓球运动的抛物线关系式,并求出点M与O的水平距离.
任务二 击球点的确定 (2)当时,运动员小亮想把球沿直线擦网击打到O点,他能不能实现,若能实现,请求出击球点位置的高度,若不能实现,请说明理由.
任务三 运动员移动的距离 (3)当时,运动员小亮的球拍A离点O的水平距离为,位于桌面上方,离桌面,且运动员挥拍的过程中,球拍的击打路线近似于一条直线,球拍与桌面的夹角为,如图3所示.当球飞行的高度在至时,小亮可以获得最佳击球效果.小亮想要成功击中乒乓球,球拍需要先向前平移,设球拍向前平移的距离为n,则n的取值范围为 ;
参考答案
1.(1)解:∵抛物线的顶点坐标为(5,8),
∴设 y=a(x-5)2+8,
把(13,0)代入,得:0=a(13-5)2+8,
解得:a=-,
∴在 y 轴右侧抛物线的函数表达式为:y=- (x-5) 2+8.
(2)解:在 中,
当 时,
答: 这个装饰物的设计高度为 .
2.(1)的值为12
(2)这个苗圃园的面积有最大值和最小值,最大值为平方米,最小值为88平方米
3.(1)解:方案①将二次函数的解析式由一般式化为顶点式可得:,
当时,取得最大值,最大值为;
②如图所示,过点作于,于,则,
设,梯形的面积为,则,
又∵,
∴,,,
;
当,
∵,
;
(2)解:由(1)的结果大致可推断出折的边数越多,面积越大,因此折的边数无限多即折的图形为半圆时面积最大.
4.(1)解:如下图建立空间直角坐标系:
则顶点坐标为,则可设抛物线的解析式为:又抛物线经过点,则解得:则抛物线的解析式为:
(2)解:由题意知: 河段水位在此基础上再涨2.1m达到最高且 灯笼底部距离水面不小于1m ,灯笼长0.4m,则灯笼悬挂点的纵坐标:所以悬挂点的纵坐标最小值为,当时解得:所以悬挂点横坐标的取值范围为:
(3)解:从顶点处开始悬挂,因为,且相邻两盏灯笼悬挂点的水平间距均为1.6m,若顶点一侧悬挂灯笼时,则顶点一侧最多悬挂15盏灯笼,此时最左边悬挂点的横坐标为:共悬挂30盏灯笼.
5.(1)y=﹣100x+5300;(2)当销售单价为35元时,月销售利润最大,最大利润是32400元.
6.(1)
(2)当时,S取得最大值,
7.(1)
(2)当时,窗户透光面积最大,与例题相比透光的最大面积变大
8.(1)李明第10天生产的粽子数量为280只.(2)第13天的利润最大,最大利润是578元.
9.(1);(2)34;2240;
10.(1);自变量的取值范围为,且x为整数
(2)每件商品售价为33元时,每个月可获得最大利润,最大利润为1950元
(3)每件商品售价为32元时,每个月可获得的利润恰好为1920元
11.(1) (2)18000元 (3)或;3800
12.任务一:,点M与O的水平距离为;任务二:不能实现;任务三:.
1 / 1
同课章节目录
