浙教版七年级数学上册第5章一元一次方程考点复习试卷(含答案)
文档属性
| 名称 | 浙教版七年级数学上册第5章一元一次方程考点复习试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 09:08:15 | ||
图片预览




文档简介
一元一次方程考点复习
一、等式的性质
1.已知等式3m=4n+2,则下列等式中不一定成立的是( )
A.3= B.3m+2=4n+4 C.3m-2=4n D.m=
2.用适当的数或式子填空,使所得结果仍是等式.
(1)如果4x=3x+15,那么 4x- =15.
(2)如果-3x=7,那么x= .
(3)如果 那么x= .
3. 判断下列一元一次方程的变形是否正确。正确的在括号里打“ ”;错误的在括号里打“×”,并改正。
(1)由2x-3=-x--4,得2x+x=-4-3。( ) ▲ .
(2)由x+3=2-4x,得5x=5。 ( ) ▲ .
(3)由 得x=-1。 ( ) ▲ .
(4)由3=x-2,得-x=--2-3。 ( ) ▲ .
二、解一元一次方程
4.解方程:.
5.解方程:.
6.解下列方程:
(1)
(2)
7.已知x=3 是方程 的解,求m的值.
8.用“☆”定义一种新运算:对于任意有理数a和b,规定.例如:.
(1)计算:;
(2)若,求的值.
三、一元一次方程解的应用
9.如果是定值,且关于x的方程,无论k为何值时,它的解总是那么的值是( )
A.15 B.16 C.17 D.18
10.已知y=1是方程2-(m-y)=2y的解,求关于x的方程m(x-3)-2= m(2x+5)的解.
11.若关于的方程与的解相同,则的值是 .
12.若关于x的方程的解与方程的解与互为相反数,求k的值.
13.小亮在解关于的一元一次方程时,发现正整数□被污染了,若老师告诉小亮这个方程的解是正整数,则被污染的正整数是多少?
14.若关于x的方程ax+b=0(a≠0)的解与关于y的方程cy+d=0(c≠0)的解满足﹣1≤x﹣y≤1,则称方程ax+b=0(a≠0)与方程cy+d=0(c≠0)是“友好方程”.例如:方程2x﹣1=0的解是x=0.5,方程y﹣1=0的解是y=1,因为﹣1≤x﹣y≤1,方程2x﹣1=0与方程y﹣1=0是“友好方程”.
(1)请通过计算判断方程2x﹣9=5x﹣2与方程5(y﹣1)﹣2(1﹣y)=﹣34﹣2y是不是“友好方程”.
(2)若关于x的方程3x﹣3+4(x﹣1)=0与关于y的方程+y=2k+1是“友好方程”,请你求出k的最大值和最小值.
四、一元一次方程的实际应用
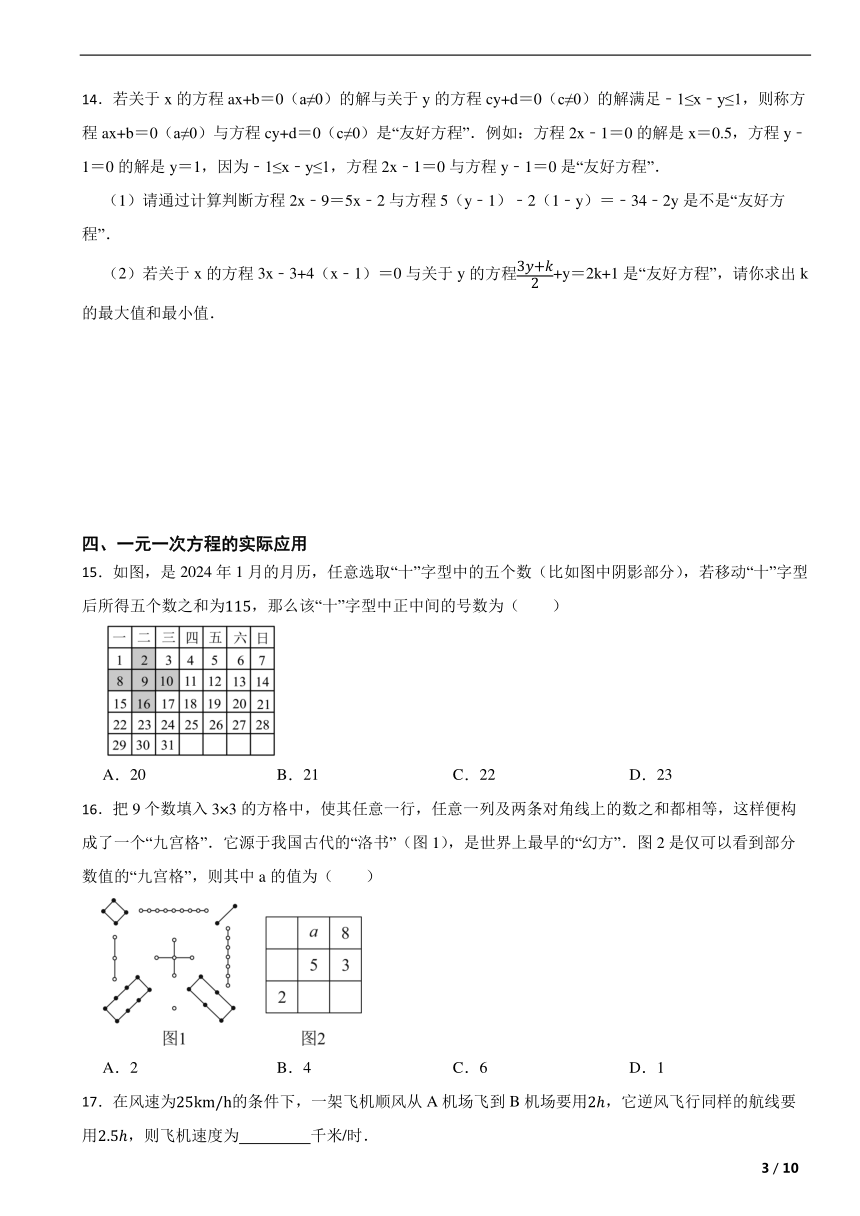
15.如图,是2024年1月的月历,任意选取“十”字型中的五个数(比如图中阴影部分),若移动“十”字型后所得五个数之和为,那么该“十”字型中正中间的号数为( )
A.20 B.21 C.22 D.23
16.把9个数填入3×3的方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中a的值为( )
A.2 B.4 C.6 D.1
17.在风速为的条件下,一架飞机顺风从A机场飞到B机场要用,它逆风飞行同样的航线要用,则飞机速度为 千米/时.
18.“办学互助”是萧红中学办学特色之一.七年18班的第一组6名同学,自行组织知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录的是5名同学的得分情况:
参赛者 A B C D E
答对题数 20 19 18 14 10
答错题数 0 1 2 6 10
得分 100 94 88 64 40
(1)由表格知,答对一题得________分,答错一题得________分;
(2)第6名同学F得了82分,请你帮他算一算,答对了几道题?
19.列一元一次方程解决实际问题(两问均需用方程求解)
第九届亚洲冬季运动会于2025年在中国黑龙江省哈尔滨市举行,而有着少数民族风格的“滨滨”“妮妮”吉祥物盲盒颇受大众关注.现有工厂生产吉祥物的盲盒,分为A、B两种包装,该工厂共有1000名工人.
(1)若该工厂生产盲盒A的人数比生产盲盒B的人数的2倍少200人,请求出生产盲盒B的工人人数;
(2)为了促销,工厂按商家要求生产盲盒大礼包,该大礼包由2个盲盒A和3个盲盒B组成.已知每个工人平均每天可以生产20个盲盒A或10个盲盒B,且每天只能生产一种包装的盲盒.该工厂应该安排多少名工人生产盲盒A,多少名工人生产盲盒B才能使每天生产的盲盒正好配套?
20.按照“双减”政策,为丰富课后托管服务内容,学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价70元,跳绳每条定价10元.某体育用品商店提供A、B两种优惠方案:
A方案:买一个篮球送一条跳绳;
B方案:篮球和跳绳都按定价的90%付款.
已知要购买篮球50个,跳绳x条()
(1)若按A方案购买,一共需付款_________元(用含x的代数式表示);若按B方案购买,一共需付款_________元(用含x的代数式表示).
(2)购买跳绳条数为多少时,两种方案的收费相同?
(3)当时,你能设计出一种最省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?
21.综合与实践:砂糖桔是广西某县传统特产,具有皮薄,汁多,化渣,味清甜,吃后沁心润喉,是老少皆宜的美味佳品.请阅读以下材料,完成学习任务:
材料一:某县批发市场计划运输一批砂糖橘到甲地出售,为保证砂糖桔新鲜需用带冷柜的货车运输.现有A,B两种型号的冷柜车,若A型车的平均速度为60千米/小时,B型车的平均速度为75千米/小时,从某县到甲地B型车比A型车少用2小时.
材料二:已知A型车每辆可运8吨,B型车每辆可运7吨,若单独租用A型车,则恰好装完:若单独租用相同数量的B型车,则还剩4吨砂糖桔没有装上车.
材料三:在材料一与材料二的条件下,冷柜车运完砂糖桔从某县到甲地时,运输的相关数据如下表所示: 路费单价冷柜使用单价1.5元/(千米辆)A型冷柜车B型冷柜车 10元/(小时·辆)8元/(小时·辆)
(参考公式:冷柜使用费=冷柜使用单价×使用时间×车辆数目;总费用=路费+冷柜使用费)
请同学们根据材料一、材料二提供的信息完成3个任务:
(1)请求出A型车从某县到甲地的时间;
(2)问这批砂糖桔共有多少吨?
(3)本次沙糖桔从某县到甲地的运输单独安排A型车或B型车,应该选用哪种车型使得总费用较少?较少的总费用是多少元?
22.研究背景:
“漏刻”是我国古代利用均匀水流导致水位变化来计时的工具.如图1,是一种漏刻的工作原理图,日天壶、夜天壶为平水壶补充水,水流经平水壶匀速流入受水壶中,在水的浮力作用下浮舟上升引起箭刻示数变化达到计时效果(为更加精准,通过分水壶使平水壶中液面高度保持不变),
研究过程:
七年级数学兴趣小组利用底面积大小相同的水壶,依据以上原理制作了一个漏刻工具模型. 图2及下表反映了受水壶中液面高度随流水时间变化的情况.
计时时间t(分钟) 15 20 25 30 …
液面高度h(厘米) 22 26 30 34 …
问题解决:依据上述信息,解决下列问题:
(1)每分钟水面上升 厘米,求液面高度为多少时开始计时?
(2)计算自计时开始45分钟时、1小时时,液面高度分别为多少?
(3)用含s的代数式表示h;
(4)自计时开始,在液面不超过受水壶总高度时,先后两次测量时差为25分钟,所测得液面高度之和为120(厘米),直接写出:这两次测量的液面高度分别为多少?
参考答案
1.A
解:A、只有当m+0时,才能得到等式,A选项符合题意;
B、由等式的性质1可得3m+2= 4n+4,B选项不符合题意;
C、由等式的性质1可得3m- 2= 4n,C选项不符合题意;
D、由等式的性质2可得m=,D选项不符合题意.
2.(1)3x
(2)-7 / 3
(3)-4
3.(1)解:(×),改正:由2x-3=-x-4,得2x+x=-4+3。
(2)解:(×),改正:由x+3=2-4x,得5x=-1。
(3)解:(×),改正:由 得
(4)( )。
4.
5.
6.(1)解:
50x=900,
x=18.
(2)解:
6x-9+3(3-x)=2,
6x-9+9-3x=2,
6x-3x=2+9-9,
3x=2,
7.解:∵x=3是方程 的解,
∴解得
8.(1);
(2)解:,,
,
∴
解得:,
的值为.
9.C
10.解:把y=1代入方程2- (m-y)=2y中,
得2- (m-1)=2,
去括号,得2-+=2,
移项、合并同类项,得-=,
解得m=1,
把m=1代人m(x-3)-2=m(2x +5)中,
得x-3-2=2x+5,
解得x=-10.
11.
解:解方程2x 1=3,得:x=2,
把x=2代入方程,得,
解得:a=.
12.
13.2
14.(1)是;(2)k的最小值为﹣,最大值为
15.D
解:设中心数为x,根据题意得:
,
解得:,
∴该“十”字型中正中间的号数为23,
16.D
17.225
18.(1)5,
(2)17
19.(1)生产盲盒的工人人数为人.
(2)该工厂应该安排名工人生产,名工人生产才能使每天生产的盲盒正好配套.
20.(1),
(2)购买150根跳绳时,A、B两种方案所需要的钱数一样多
(3)按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款3950元
21.(1)A型车从某县到甲地的时间为10小时;
(2)这批砂糖橘共有 32吨
(3)单独安排A 型车运输才能使得本次总费用较少,较少的总费用是4000元
22.(1);
(2)厘米,厘米
(3)
(4)厘米,厘米
1 / 1
一、等式的性质
1.已知等式3m=4n+2,则下列等式中不一定成立的是( )
A.3= B.3m+2=4n+4 C.3m-2=4n D.m=
2.用适当的数或式子填空,使所得结果仍是等式.
(1)如果4x=3x+15,那么 4x- =15.
(2)如果-3x=7,那么x= .
(3)如果 那么x= .
3. 判断下列一元一次方程的变形是否正确。正确的在括号里打“ ”;错误的在括号里打“×”,并改正。
(1)由2x-3=-x--4,得2x+x=-4-3。( ) ▲ .
(2)由x+3=2-4x,得5x=5。 ( ) ▲ .
(3)由 得x=-1。 ( ) ▲ .
(4)由3=x-2,得-x=--2-3。 ( ) ▲ .
二、解一元一次方程
4.解方程:.
5.解方程:.
6.解下列方程:
(1)
(2)
7.已知x=3 是方程 的解,求m的值.
8.用“☆”定义一种新运算:对于任意有理数a和b,规定.例如:.
(1)计算:;
(2)若,求的值.
三、一元一次方程解的应用
9.如果是定值,且关于x的方程,无论k为何值时,它的解总是那么的值是( )
A.15 B.16 C.17 D.18
10.已知y=1是方程2-(m-y)=2y的解,求关于x的方程m(x-3)-2= m(2x+5)的解.
11.若关于的方程与的解相同,则的值是 .
12.若关于x的方程的解与方程的解与互为相反数,求k的值.
13.小亮在解关于的一元一次方程时,发现正整数□被污染了,若老师告诉小亮这个方程的解是正整数,则被污染的正整数是多少?
14.若关于x的方程ax+b=0(a≠0)的解与关于y的方程cy+d=0(c≠0)的解满足﹣1≤x﹣y≤1,则称方程ax+b=0(a≠0)与方程cy+d=0(c≠0)是“友好方程”.例如:方程2x﹣1=0的解是x=0.5,方程y﹣1=0的解是y=1,因为﹣1≤x﹣y≤1,方程2x﹣1=0与方程y﹣1=0是“友好方程”.
(1)请通过计算判断方程2x﹣9=5x﹣2与方程5(y﹣1)﹣2(1﹣y)=﹣34﹣2y是不是“友好方程”.
(2)若关于x的方程3x﹣3+4(x﹣1)=0与关于y的方程+y=2k+1是“友好方程”,请你求出k的最大值和最小值.
四、一元一次方程的实际应用
15.如图,是2024年1月的月历,任意选取“十”字型中的五个数(比如图中阴影部分),若移动“十”字型后所得五个数之和为,那么该“十”字型中正中间的号数为( )
A.20 B.21 C.22 D.23
16.把9个数填入3×3的方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中a的值为( )
A.2 B.4 C.6 D.1
17.在风速为的条件下,一架飞机顺风从A机场飞到B机场要用,它逆风飞行同样的航线要用,则飞机速度为 千米/时.
18.“办学互助”是萧红中学办学特色之一.七年18班的第一组6名同学,自行组织知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录的是5名同学的得分情况:
参赛者 A B C D E
答对题数 20 19 18 14 10
答错题数 0 1 2 6 10
得分 100 94 88 64 40
(1)由表格知,答对一题得________分,答错一题得________分;
(2)第6名同学F得了82分,请你帮他算一算,答对了几道题?
19.列一元一次方程解决实际问题(两问均需用方程求解)
第九届亚洲冬季运动会于2025年在中国黑龙江省哈尔滨市举行,而有着少数民族风格的“滨滨”“妮妮”吉祥物盲盒颇受大众关注.现有工厂生产吉祥物的盲盒,分为A、B两种包装,该工厂共有1000名工人.
(1)若该工厂生产盲盒A的人数比生产盲盒B的人数的2倍少200人,请求出生产盲盒B的工人人数;
(2)为了促销,工厂按商家要求生产盲盒大礼包,该大礼包由2个盲盒A和3个盲盒B组成.已知每个工人平均每天可以生产20个盲盒A或10个盲盒B,且每天只能生产一种包装的盲盒.该工厂应该安排多少名工人生产盲盒A,多少名工人生产盲盒B才能使每天生产的盲盒正好配套?
20.按照“双减”政策,为丰富课后托管服务内容,学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价70元,跳绳每条定价10元.某体育用品商店提供A、B两种优惠方案:
A方案:买一个篮球送一条跳绳;
B方案:篮球和跳绳都按定价的90%付款.
已知要购买篮球50个,跳绳x条()
(1)若按A方案购买,一共需付款_________元(用含x的代数式表示);若按B方案购买,一共需付款_________元(用含x的代数式表示).
(2)购买跳绳条数为多少时,两种方案的收费相同?
(3)当时,你能设计出一种最省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?
21.综合与实践:砂糖桔是广西某县传统特产,具有皮薄,汁多,化渣,味清甜,吃后沁心润喉,是老少皆宜的美味佳品.请阅读以下材料,完成学习任务:
材料一:某县批发市场计划运输一批砂糖橘到甲地出售,为保证砂糖桔新鲜需用带冷柜的货车运输.现有A,B两种型号的冷柜车,若A型车的平均速度为60千米/小时,B型车的平均速度为75千米/小时,从某县到甲地B型车比A型车少用2小时.
材料二:已知A型车每辆可运8吨,B型车每辆可运7吨,若单独租用A型车,则恰好装完:若单独租用相同数量的B型车,则还剩4吨砂糖桔没有装上车.
材料三:在材料一与材料二的条件下,冷柜车运完砂糖桔从某县到甲地时,运输的相关数据如下表所示: 路费单价冷柜使用单价1.5元/(千米辆)A型冷柜车B型冷柜车 10元/(小时·辆)8元/(小时·辆)
(参考公式:冷柜使用费=冷柜使用单价×使用时间×车辆数目;总费用=路费+冷柜使用费)
请同学们根据材料一、材料二提供的信息完成3个任务:
(1)请求出A型车从某县到甲地的时间;
(2)问这批砂糖桔共有多少吨?
(3)本次沙糖桔从某县到甲地的运输单独安排A型车或B型车,应该选用哪种车型使得总费用较少?较少的总费用是多少元?
22.研究背景:
“漏刻”是我国古代利用均匀水流导致水位变化来计时的工具.如图1,是一种漏刻的工作原理图,日天壶、夜天壶为平水壶补充水,水流经平水壶匀速流入受水壶中,在水的浮力作用下浮舟上升引起箭刻示数变化达到计时效果(为更加精准,通过分水壶使平水壶中液面高度保持不变),
研究过程:
七年级数学兴趣小组利用底面积大小相同的水壶,依据以上原理制作了一个漏刻工具模型. 图2及下表反映了受水壶中液面高度随流水时间变化的情况.
计时时间t(分钟) 15 20 25 30 …
液面高度h(厘米) 22 26 30 34 …
问题解决:依据上述信息,解决下列问题:
(1)每分钟水面上升 厘米,求液面高度为多少时开始计时?
(2)计算自计时开始45分钟时、1小时时,液面高度分别为多少?
(3)用含s的代数式表示h;
(4)自计时开始,在液面不超过受水壶总高度时,先后两次测量时差为25分钟,所测得液面高度之和为120(厘米),直接写出:这两次测量的液面高度分别为多少?
参考答案
1.A
解:A、只有当m+0时,才能得到等式,A选项符合题意;
B、由等式的性质1可得3m+2= 4n+4,B选项不符合题意;
C、由等式的性质1可得3m- 2= 4n,C选项不符合题意;
D、由等式的性质2可得m=,D选项不符合题意.
2.(1)3x
(2)-7 / 3
(3)-4
3.(1)解:(×),改正:由2x-3=-x-4,得2x+x=-4+3。
(2)解:(×),改正:由x+3=2-4x,得5x=-1。
(3)解:(×),改正:由 得
(4)( )。
4.
5.
6.(1)解:
50x=900,
x=18.
(2)解:
6x-9+3(3-x)=2,
6x-9+9-3x=2,
6x-3x=2+9-9,
3x=2,
7.解:∵x=3是方程 的解,
∴解得
8.(1);
(2)解:,,
,
∴
解得:,
的值为.
9.C
10.解:把y=1代入方程2- (m-y)=2y中,
得2- (m-1)=2,
去括号,得2-+=2,
移项、合并同类项,得-=,
解得m=1,
把m=1代人m(x-3)-2=m(2x +5)中,
得x-3-2=2x+5,
解得x=-10.
11.
解:解方程2x 1=3,得:x=2,
把x=2代入方程,得,
解得:a=.
12.
13.2
14.(1)是;(2)k的最小值为﹣,最大值为
15.D
解:设中心数为x,根据题意得:
,
解得:,
∴该“十”字型中正中间的号数为23,
16.D
17.225
18.(1)5,
(2)17
19.(1)生产盲盒的工人人数为人.
(2)该工厂应该安排名工人生产,名工人生产才能使每天生产的盲盒正好配套.
20.(1),
(2)购买150根跳绳时,A、B两种方案所需要的钱数一样多
(3)按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款3950元
21.(1)A型车从某县到甲地的时间为10小时;
(2)这批砂糖橘共有 32吨
(3)单独安排A 型车运输才能使得本次总费用较少,较少的总费用是4000元
22.(1);
(2)厘米,厘米
(3)
(4)厘米,厘米
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
