二次函数复习学案(期中)
图片预览
文档简介
二次函数复习学案
姓名
【复习目标】
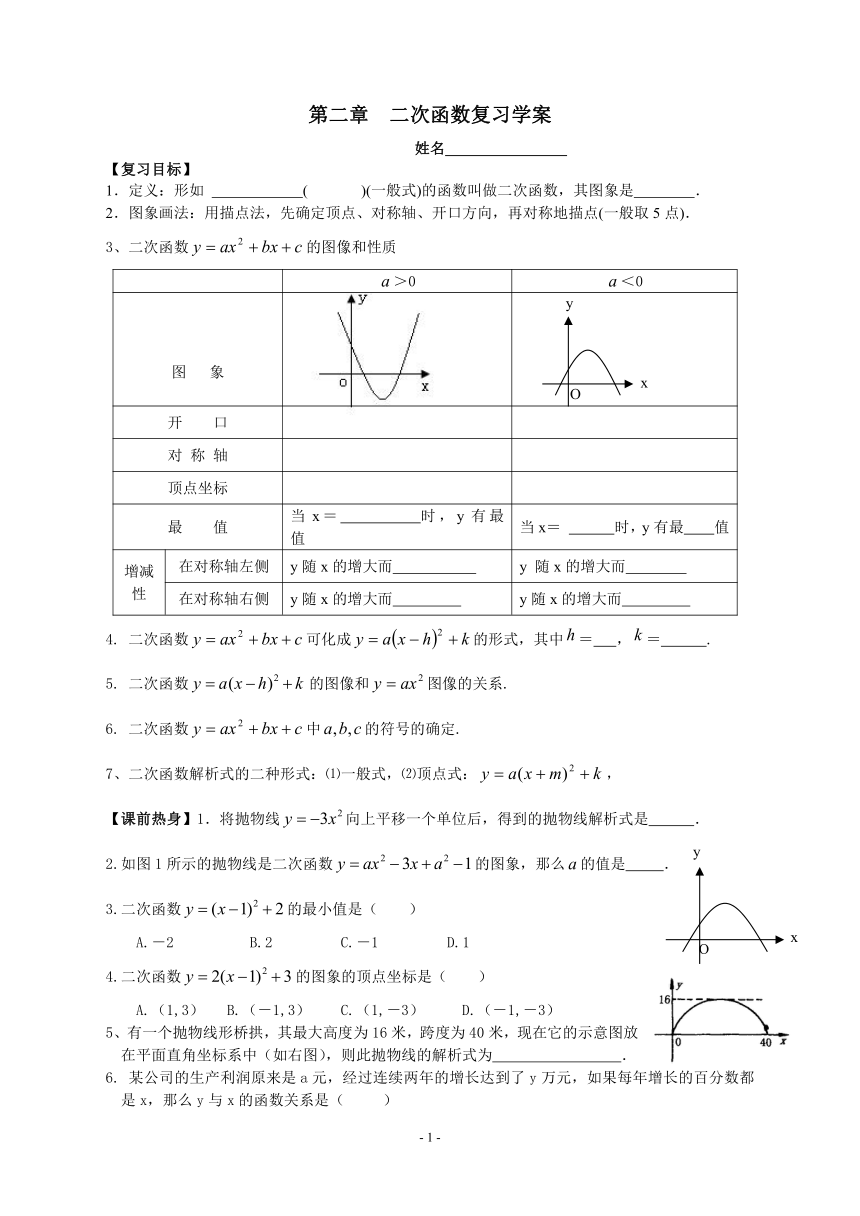
1.定义:形如 ( )(一般式)的函数叫做二次函数,其图象是 .
2.图象画法:用描点法,先确定顶点、对称轴、开口方向,再对称地描点(一般取5点).
3、二次函数的图像和性质
>0 <0
图 象
开 口
对 称 轴
顶点坐标
最 值 当x= 时,y有最 值 当x= 时,y有最 值
增减性 在对称轴左侧 y随x的增大而 y 随x的增大而
在对称轴右侧 y随x的增大而 y随x的增大而
4. 二次函数可化成的形式,其中= ,= .
5. 二次函数的图像和图像的关系.
6. 二次函数中的符号的确定.
7、二次函数解析式的二种形式:⑴一般式,⑵顶点式:,
【课前热身】1.将抛物线向上平移一个单位后,得到的抛物线解析式是 .
2.如图1所示的抛物线是二次函数的图象,那么的值是 .
3.二次函数的最小值是( )
A.-2 B.2 C.-1 D.1
4.二次函数的图象的顶点坐标是( )
A.(1,3) B.(-1,3) C.(1,-3) D.(-1,-3)
5、有一个抛物线形桥拱,其最大高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系中(如右图),则此抛物线的解析式为 .
6. 某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y= a(x-1)2 C.y=a(1-x)2 D.y=a(l+x)2
7. 把一段长1.6米的铁丝围长方形ABCD,设宽为x,面积为y.则当y最大时,x所取的值是( )
A.0.5 B.0.4 C.0.3 D.0.6
【典例精析】
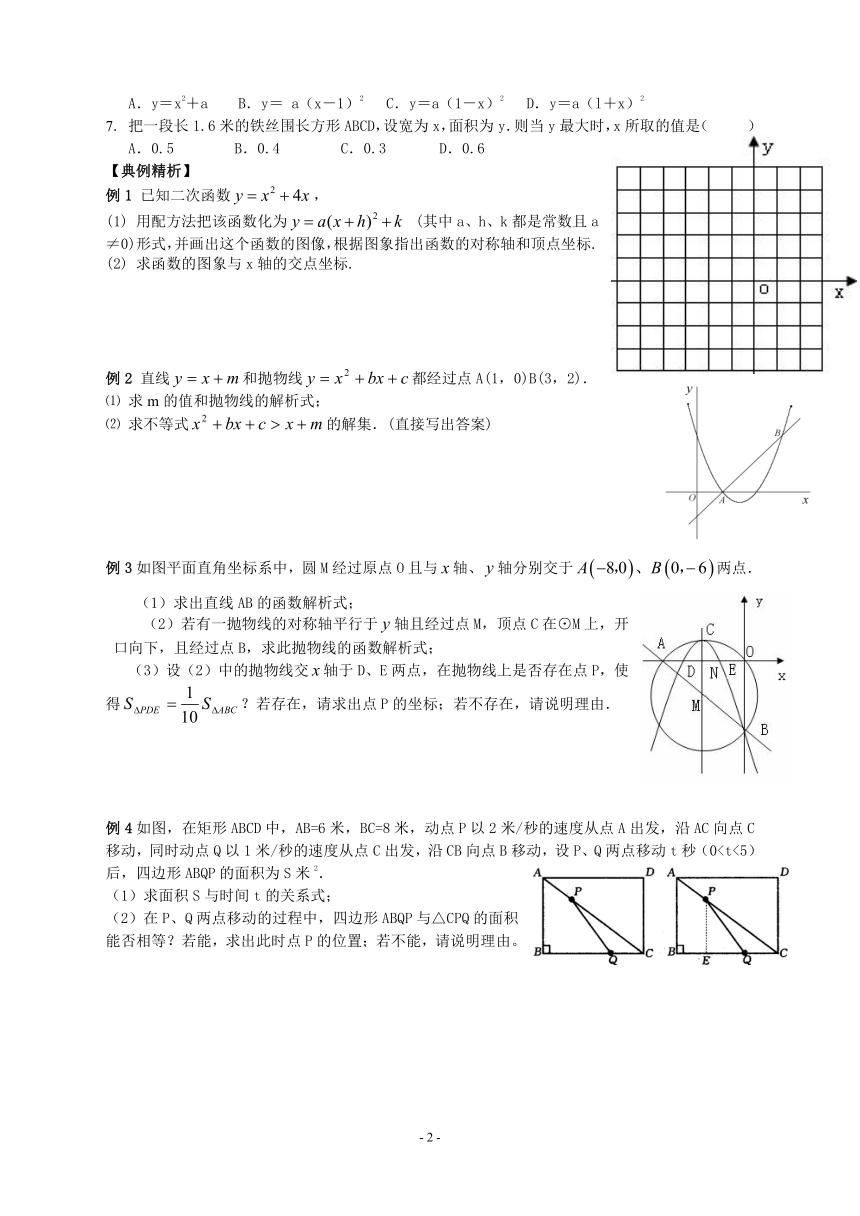
例1 已知二次函数,
(1) 用配方法把该函数化为 (其中a、h、k都是常数且a≠0)形式,并画出这个函数的图像,根据图象指出函数的对称轴和顶点坐标.
(2) 求函数的图象与x轴的交点坐标.
例2 直线和抛物线都经过点A(1,0)B(3,2).
⑴ 求m的值和抛物线的解析式;
⑵ 求不等式的解集.(直接写出答案)
例3如图平面直角坐标系中,圆M经过原点O且与轴、轴分别交于两点.
(1)求出直线AB的函数解析式;
(2)若有一抛物线的对称轴平行于轴且经过点M,顶点C在⊙M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交轴于D、E两点,在抛物线上是否存在点P,使得?若存在,请求出点P的坐标;若不存在,请说明理由.
例4如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
例5 我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价(元∕件) …… 30 40 50 60 ……
每天销售量(件) …… 500 400 300 200 ……
(1)把上表中、的各组对应值作为点的坐标,在平面直角坐标系中描出相应的点,猜想与的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
解:
【演练提高】
已知二次函数
2、求满足下列条件的二次函数解析式:
⑴图象过(1,0)、(0,-2)和(2,3)。 ⑵图象与x轴的交点的横坐标为-2和1,且过点(2,4)。
⑶当x=2时,y=3,且过点(1,-3)。
3.已知二次函数的部分图象如右图所示,则关于的一元二次方程的解为 .
4. 函数与在同一坐标系中的大致图象是( )
5、已知函数y=x2-2x-2的图象如图,根据其中提供信息,可求得使y≥1成立的x取值范围是( )
A.-1≤x≤3 B.-3≤x≤1 C.x≥-3 D.x≤-1或x≥3
6.二次函数()的图象如图所示,则下列结论:
①>0; ②>0; ③ b2-4>0,其中正确的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
(第5题) (第6题)
7.一座拱型桥,桥下水面宽度AB是20米,拱高CD是4米.若水面上升3米至EF,则水面宽度EF是多少
(1)若把它看作是抛物线的一部分,在坐标系中(如图①)可设抛物线的表达式为.
请你填空: ,= ,EF= 米.
(2)若把它看作是圆的一部分,则可构造图形(如图②)计算如下:
设圆的半径是r米,在Rt△OCB中,易知 ,.
同理,当水面上升3米至EF,在Rt△OGF中可计算出,即水面宽度米.
请估计上面EF与(1)中你计算的EF的差的近似值(误差小于0.1米).
y
x
O
y
x
O
10 20 30 40 50 60 70 80
100
200
300
400
500
600
700
800
0
⑴开口方向: ⑵对称轴:
⑶顶点坐标:
⑷图象与x轴的交点坐标:
⑸图象与y轴的交点坐标:
⑹图象与y轴的交点关于对称轴的对称点的坐标:
⑺用五点法画函数的草图
⑻求这个函数的最值,当x= 时,
⑼当 时;y=0,
当 时,y>0;当 时,y<0。
⑽图象在x轴上截得的线段的长是:
⑾求图象与坐标轴交点所围成的三角形的面积:
⑿根据图像回答:当x 时,y随x的增大而增大,当x 时,y随x的增大而减小。
⒀求该函数关于x轴对称的函数解析式:
求该函数关于y轴对称的函数解析式:
PAGE
姓名
【复习目标】
1.定义:形如 ( )(一般式)的函数叫做二次函数,其图象是 .
2.图象画法:用描点法,先确定顶点、对称轴、开口方向,再对称地描点(一般取5点).
3、二次函数的图像和性质
>0 <0
图 象
开 口
对 称 轴
顶点坐标
最 值 当x= 时,y有最 值 当x= 时,y有最 值
增减性 在对称轴左侧 y随x的增大而 y 随x的增大而
在对称轴右侧 y随x的增大而 y随x的增大而
4. 二次函数可化成的形式,其中= ,= .
5. 二次函数的图像和图像的关系.
6. 二次函数中的符号的确定.
7、二次函数解析式的二种形式:⑴一般式,⑵顶点式:,
【课前热身】1.将抛物线向上平移一个单位后,得到的抛物线解析式是 .
2.如图1所示的抛物线是二次函数的图象,那么的值是 .
3.二次函数的最小值是( )
A.-2 B.2 C.-1 D.1
4.二次函数的图象的顶点坐标是( )
A.(1,3) B.(-1,3) C.(1,-3) D.(-1,-3)
5、有一个抛物线形桥拱,其最大高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系中(如右图),则此抛物线的解析式为 .
6. 某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y= a(x-1)2 C.y=a(1-x)2 D.y=a(l+x)2
7. 把一段长1.6米的铁丝围长方形ABCD,设宽为x,面积为y.则当y最大时,x所取的值是( )
A.0.5 B.0.4 C.0.3 D.0.6
【典例精析】
例1 已知二次函数,
(1) 用配方法把该函数化为 (其中a、h、k都是常数且a≠0)形式,并画出这个函数的图像,根据图象指出函数的对称轴和顶点坐标.
(2) 求函数的图象与x轴的交点坐标.
例2 直线和抛物线都经过点A(1,0)B(3,2).
⑴ 求m的值和抛物线的解析式;
⑵ 求不等式的解集.(直接写出答案)
例3如图平面直角坐标系中,圆M经过原点O且与轴、轴分别交于两点.
(1)求出直线AB的函数解析式;
(2)若有一抛物线的对称轴平行于轴且经过点M,顶点C在⊙M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交轴于D、E两点,在抛物线上是否存在点P,使得?若存在,请求出点P的坐标;若不存在,请说明理由.
例4如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
例5 我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价(元∕件) …… 30 40 50 60 ……
每天销售量(件) …… 500 400 300 200 ……
(1)把上表中、的各组对应值作为点的坐标,在平面直角坐标系中描出相应的点,猜想与的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
解:
【演练提高】
已知二次函数
2、求满足下列条件的二次函数解析式:
⑴图象过(1,0)、(0,-2)和(2,3)。 ⑵图象与x轴的交点的横坐标为-2和1,且过点(2,4)。
⑶当x=2时,y=3,且过点(1,-3)。
3.已知二次函数的部分图象如右图所示,则关于的一元二次方程的解为 .
4. 函数与在同一坐标系中的大致图象是( )
5、已知函数y=x2-2x-2的图象如图,根据其中提供信息,可求得使y≥1成立的x取值范围是( )
A.-1≤x≤3 B.-3≤x≤1 C.x≥-3 D.x≤-1或x≥3
6.二次函数()的图象如图所示,则下列结论:
①>0; ②>0; ③ b2-4>0,其中正确的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
(第5题) (第6题)
7.一座拱型桥,桥下水面宽度AB是20米,拱高CD是4米.若水面上升3米至EF,则水面宽度EF是多少
(1)若把它看作是抛物线的一部分,在坐标系中(如图①)可设抛物线的表达式为.
请你填空: ,= ,EF= 米.
(2)若把它看作是圆的一部分,则可构造图形(如图②)计算如下:
设圆的半径是r米,在Rt△OCB中,易知 ,.
同理,当水面上升3米至EF,在Rt△OGF中可计算出,即水面宽度米.
请估计上面EF与(1)中你计算的EF的差的近似值(误差小于0.1米).
y
x
O
y
x
O
10 20 30 40 50 60 70 80
100
200
300
400
500
600
700
800
0
⑴开口方向: ⑵对称轴:
⑶顶点坐标:
⑷图象与x轴的交点坐标:
⑸图象与y轴的交点坐标:
⑹图象与y轴的交点关于对称轴的对称点的坐标:
⑺用五点法画函数的草图
⑻求这个函数的最值,当x= 时,
⑼当 时;y=0,
当 时,y>0;当 时,y<0。
⑽图象在x轴上截得的线段的长是:
⑾求图象与坐标轴交点所围成的三角形的面积:
⑿根据图像回答:当x 时,y随x的增大而增大,当x 时,y随x的增大而减小。
⒀求该函数关于x轴对称的函数解析式:
求该函数关于y轴对称的函数解析式:
PAGE
同课章节目录
