6.4 线段的和差 课件(共23张PPT)
文档属性
| 名称 | 6.4 线段的和差 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-05 12:42:51 | ||
图片预览







文档简介
(共23张PPT)
6.4 线段的和差
浙教版七年级上册
如图,已知线段a=1.5cm,b=2.5cm,c=4cm
a
b
c
∵ 1.5+2.5=4
线段c的长度是线段a与b的长度的和,
我们就说线段c是线段a与b的和,
记作:c = a+b
∵ 4-2.5=1.5
线段a的长度是线段c与b的长度的差,
我们就说线段a是线段c与b的差,
记作:a = c-b
两条线段的和或差,仍是一条线段。
温故知新:
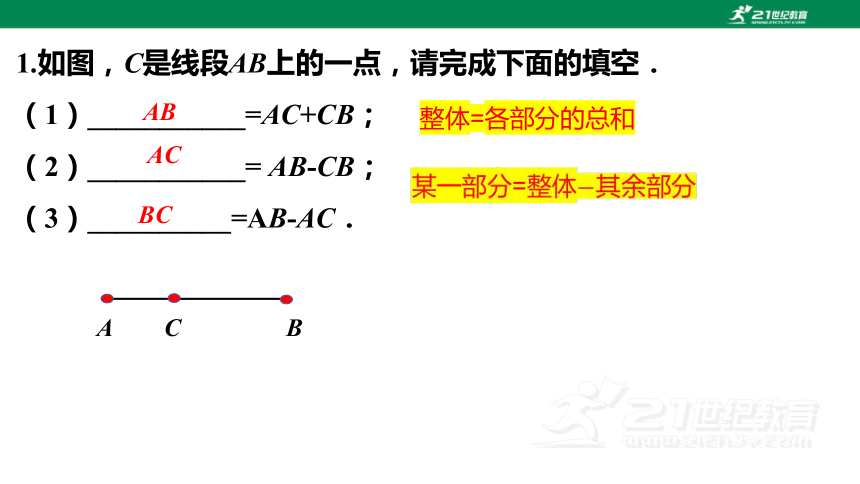
1.如图,C是线段AB上的一点,请完成下面的填空.
(1)___________=AC+CB;
(2)___________= AB-CB;
(3)__________=AB-AC.
AB
AC
BC
A
C
B
AC=
OF=
a-b;
a+c-2b
下列四个图中,能表示线段x+b=a+c 的是( )
D
2. 如图,AC = DB,则图中另外两条相等的线段为_____________.
A C D B
AD=BC
∵ AC=DB
∴ AC+CD=DB+CD
(等量+等量,其和相等)
∴ AD=BC
3. 如图,AD = BC,则图中另外两条相等的线段为_____________.
A C D B
AC=DB
∵ AD=BC
∴ AC=DB
21世纪教育网
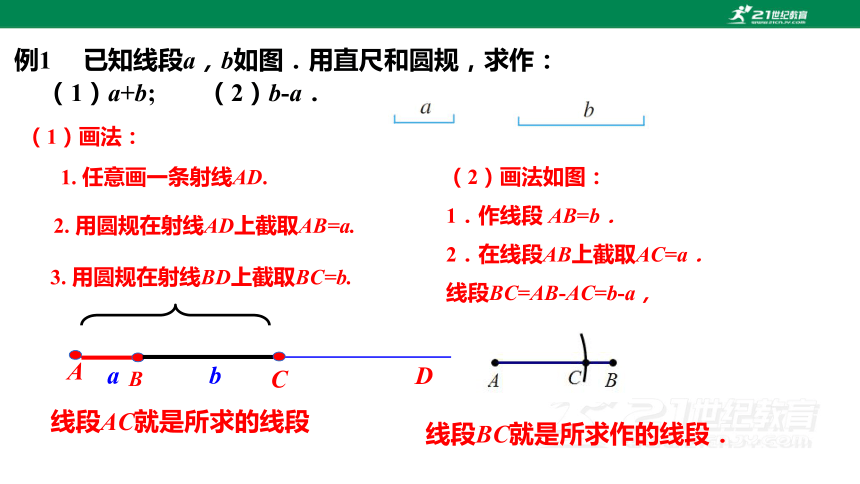
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
线段AC就是所求的线段
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
A
D
a
B
b
C
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,
线段BC就是所求作的线段.
拿出一张白纸,对折这张白纸.把白纸展开铺平,
发现在边AB上有个折痕点C,请问AC和BC相等吗?
A
B
C
点C具有什么特殊的位置?
请你给它起一个名字,并描述这一位置的特征.
AC=BC
点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点.
几何语言:
∵点C是线段AB的中点,
如图:如果点C是线段AB的中点,那么就有AC=BC.
∵点C是线段AB的中点,∴
∵点C是线段AB的中点,∴
∴
AB=2AC=2BC
AC=BC.
点 M , N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
点 M , N ,P是线段 AB 的四等分点:
N
M
B
A
P
AM = MN = NP =PB= ___ AB
(或 AB = ___AM = ___ MN = ___NP= ___PB)
4
4
4
4
1.如图,已知C是线段AB的中点,点D是线段AC的中点.
请完成下列填空.
(1) AB = BC .
(2) AD = AC .
(3) BD = AD .
2
1
2
3
2、如图,点C、D把线段AB三等分,AC=n,
⑴ CD=BD=AC= ,AB= ;
⑵ 点C是线段 的中点,
线段BC的中点是点 。
n
3n
AD
D
⑶在上述条件下,若点P是线段AB的中点,
AP= , CP=
A
D
C
B
P
n
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
解:∵点P是线段AB的中点,
∵点C,D把线段AB三等分,
∴AB=6CP=6×1.5=9(cm)
C
A
B
D
P
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
1.5
x=9
1.若点P在线段AB上,E、F分别是AP和BP的中点.
(1)若AP=8,BP=6,求线段EF的长;
4
3
A
B
P
E
F
8
6
(2)若线段AP=a,BP=b,求线段EF的长;
A
B
P
E
F
a
b
1
2
a
1
2
b
夯实基础,稳扎稳打
2、 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,
那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
当点C在AB之间上,
AC=AB-BC=1cm;
C
当点C在AB的延长线上时,
AC=AB+BC=9cm.
1
2
a
a
a
1
2
a
5.已知线段AC=1,BC=3
则线段AB的长度是( )
A.4 B.2 C.2或4 D.非以上答案
D
A
C
B
点B位置在哪里?
连续递推,豁然开朗
6.线段AB=13 cm,MA+MB=17 cm,下列说法正确的是( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
D
A
B
M1
M2
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.4 线段的和差
浙教版七年级上册
如图,已知线段a=1.5cm,b=2.5cm,c=4cm
a
b
c
∵ 1.5+2.5=4
线段c的长度是线段a与b的长度的和,
我们就说线段c是线段a与b的和,
记作:c = a+b
∵ 4-2.5=1.5
线段a的长度是线段c与b的长度的差,
我们就说线段a是线段c与b的差,
记作:a = c-b
两条线段的和或差,仍是一条线段。
温故知新:
1.如图,C是线段AB上的一点,请完成下面的填空.
(1)___________=AC+CB;
(2)___________= AB-CB;
(3)__________=AB-AC.
AB
AC
BC
A
C
B
AC=
OF=
a-b;
a+c-2b
下列四个图中,能表示线段x+b=a+c 的是( )
D
2. 如图,AC = DB,则图中另外两条相等的线段为_____________.
A C D B
AD=BC
∵ AC=DB
∴ AC+CD=DB+CD
(等量+等量,其和相等)
∴ AD=BC
3. 如图,AD = BC,则图中另外两条相等的线段为_____________.
A C D B
AC=DB
∵ AD=BC
∴ AC=DB
21世纪教育网
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
线段AC就是所求的线段
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
A
D
a
B
b
C
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,
线段BC就是所求作的线段.
拿出一张白纸,对折这张白纸.把白纸展开铺平,
发现在边AB上有个折痕点C,请问AC和BC相等吗?
A
B
C
点C具有什么特殊的位置?
请你给它起一个名字,并描述这一位置的特征.
AC=BC
点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点.
几何语言:
∵点C是线段AB的中点,
如图:如果点C是线段AB的中点,那么就有AC=BC.
∵点C是线段AB的中点,∴
∵点C是线段AB的中点,∴
∴
AB=2AC=2BC
AC=BC.
点 M , N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
点 M , N ,P是线段 AB 的四等分点:
N
M
B
A
P
AM = MN = NP =PB= ___ AB
(或 AB = ___AM = ___ MN = ___NP= ___PB)
4
4
4
4
1.如图,已知C是线段AB的中点,点D是线段AC的中点.
请完成下列填空.
(1) AB = BC .
(2) AD = AC .
(3) BD = AD .
2
1
2
3
2、如图,点C、D把线段AB三等分,AC=n,
⑴ CD=BD=AC= ,AB= ;
⑵ 点C是线段 的中点,
线段BC的中点是点 。
n
3n
AD
D
⑶在上述条件下,若点P是线段AB的中点,
AP= , CP=
A
D
C
B
P
n
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
解:∵点P是线段AB的中点,
∵点C,D把线段AB三等分,
∴AB=6CP=6×1.5=9(cm)
C
A
B
D
P
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
1.5
x=9
1.若点P在线段AB上,E、F分别是AP和BP的中点.
(1)若AP=8,BP=6,求线段EF的长;
4
3
A
B
P
E
F
8
6
(2)若线段AP=a,BP=b,求线段EF的长;
A
B
P
E
F
a
b
1
2
a
1
2
b
夯实基础,稳扎稳打
2、 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,
那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
当点C在AB之间上,
AC=AB-BC=1cm;
C
当点C在AB的延长线上时,
AC=AB+BC=9cm.
1
2
a
a
a
1
2
a
5.已知线段AC=1,BC=3
则线段AB的长度是( )
A.4 B.2 C.2或4 D.非以上答案
D
A
C
B
点B位置在哪里?
连续递推,豁然开朗
6.线段AB=13 cm,MA+MB=17 cm,下列说法正确的是( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
D
A
B
M1
M2
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
