5.4一次函数的图象与性质 分知识点练习(含答案)浙教版数学八年级上册
文档属性
| 名称 | 5.4一次函数的图象与性质 分知识点练习(含答案)浙教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 279.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 13:34:42 | ||
图片预览



文档简介
5.4一次函数的图象与性质
知识点1 正比例函数图象
1.已知正比例函数,当时,,则下列各点中在该函数图象上的是( )
A. B. C. D.
2.已知正比例函数的图象过点,则k= .
3.如果正比例函数的图象经过第二、四象限,那么k的取值范围是 .
4.已知:如图点在正比例函数图象上,点B坐标为,连接,,点C是线段的中点,点P在线段上以每秒2个单位的速度由点B向点O运动,点Q在线段上由点A向点O运动,P、Q两点同时运动,同时停止,运动时间为t秒
(1)求该正比例函数的解析式:
(2)当秒,且时,求点Q的坐标:
(3)连接,在点P、Q运动过程中,与是否全等?如果全等,请求出点Q的运动速度;如果不全等,请说明理由
知识点2 一次函数图象
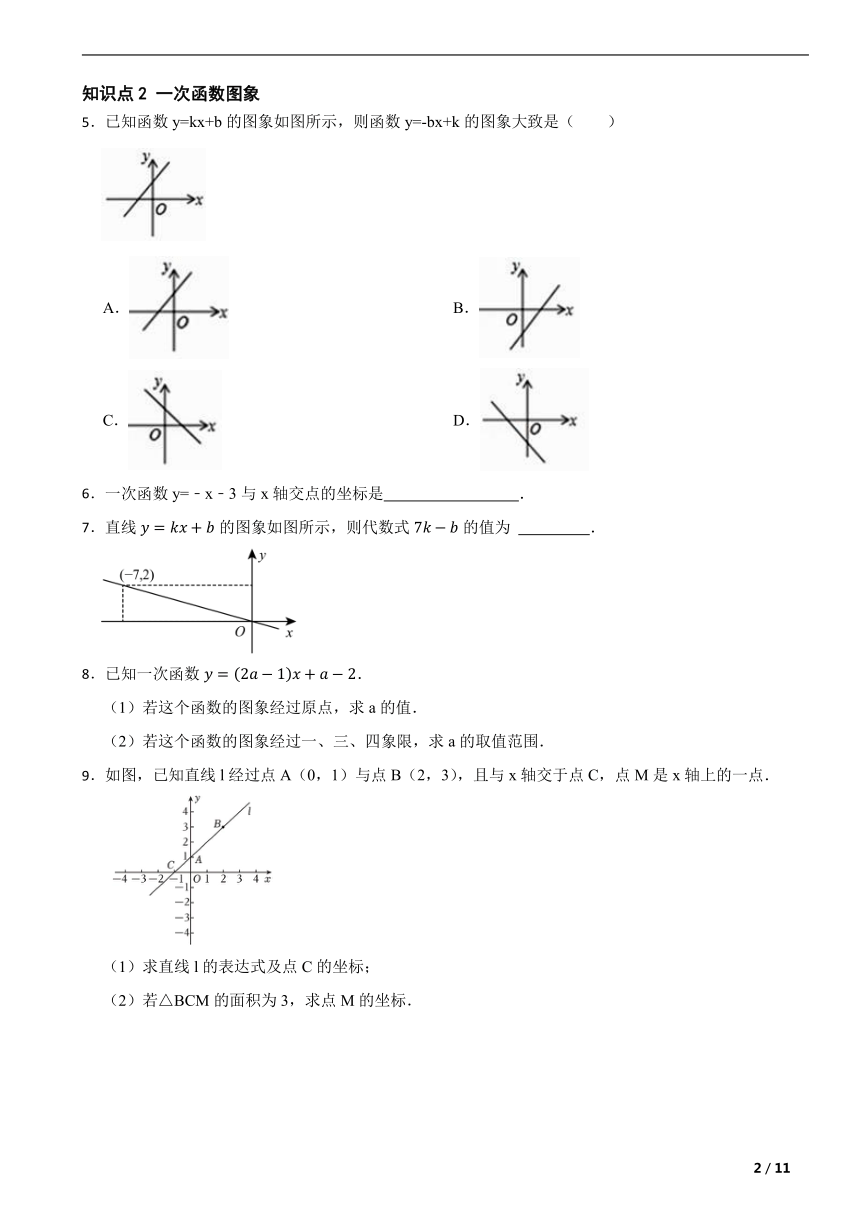
5.已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )
A. B.
C. D.
6.一次函数y=﹣x﹣3与x轴交点的坐标是 .
7.直线的图象如图所示,则代数式的值为 .
8.已知一次函数.
(1)若这个函数的图象经过原点,求a的值.
(2)若这个函数的图象经过一、三、四象限,求a的取值范围.
9.如图,已知直线l经过点A(0,1)与点B(2,3),且与x轴交于点C,点M是x轴上的一点.
(1)求直线l的表达式及点C的坐标;
(2)若△BCM的面积为3,求点M的坐标.
知识点3 一次函数的性质
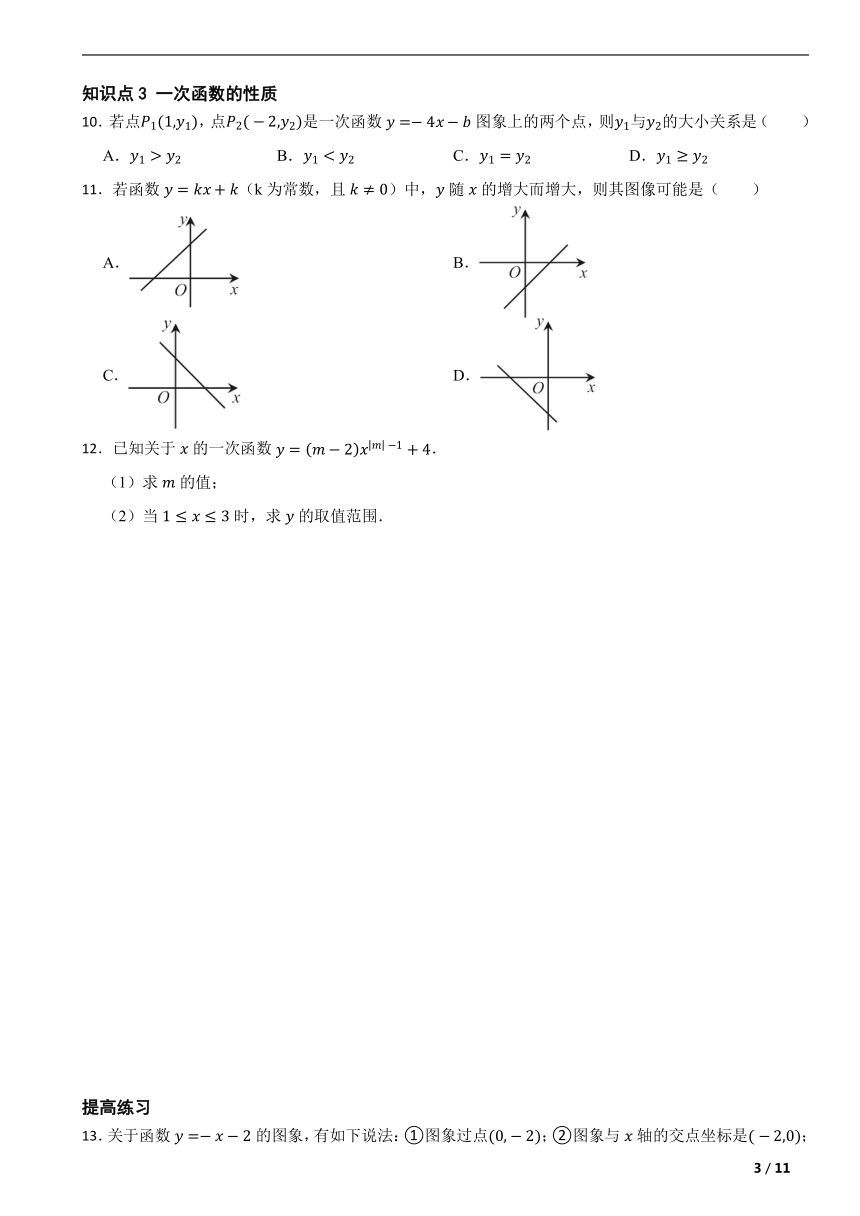
10.若点,点是一次函数图象上的两个点,则与的大小关系是( )
A. B. C. D.
11.若函数(k为常数,且)中,随的增大而增大,则其图像可能是( )
A. B.
C. D.
12.已知关于的一次函数.
(1)求的值;
(2)当时,求的取值范围.
提高练习
13.关于函数的图象,有如下说法:①图象过点;②图象与轴的交点坐标是;③从图象知随的增大而增大;④图象不过第一象限;⑤图象与函数的图象平行,其中正确的说法有( )
A.2个 B.3个 C.4个 D.5个
14.已知直线上横、纵坐标都是整数的点的个数是
A.0个 B.1个
C.不少于2个但有限个 D.无数个
15.已知与是一次函数.若,那么如图所示的个图中正确的是( )
A. B.
C. D.
16.定义一种新运算:,例如:,,给出下列说法:
①;
②若,则或4;
③的解集为或;
④若函数的图象与直线(m为常数)只有1个交点,则.
以上说法中正确的个数为( )
A.1 B.2 C.3 D.4
17.已知,如图,平面直角坐标系中,直线与坐标轴交于A、B两点,直线与坐标轴交于C、D两点,两直线交于点;点是轴上一动点,连接ME,将沿ME翻折,点对应点刚好落在轴负半轴上,则ME所在直线解析式为( )
A. B. C. D.
18.已知是直线(为常数)上的三个点,则的大小关系是 (用“”表示).
19.若关于x的一次函数的图象经过点和点,当时,,且与y轴相交于正半轴,则整数m的值为 .
20.已知一次函数的图象在y轴上的截距与一次函数的图象在y轴上的截距互为相反数,则 .
21.如图所示,一次函数的图象与轴交于点,与轴交于点,是轴上一动点,连接,将沿所在的直线折叠,当点落在轴上时,点的坐标为 .
22.设一次函数(,为常数,)的图象经过,两点.
(1)求该函数的表达式;
(2)若点在该函数的图象上,求的值;
(3)设点在轴上,若,求点的坐标.
23.如图,直线与x轴相交于点A,与y轴相交于点 B.
(1)直接写出的面积;
(2)若C为y轴上一点,且的面积是,求点C的坐标;
(3)若P是x轴上一点,且,求P的坐标.
24.已知直线与直线.
(1)求两直线交点C的坐标;
(2)求的面积.
(3)在直线上能否找到点P,使得,若能,请求出点P的坐标,若不能请说明理由.
参考答案
1.B
2.
3.
4.(1)
(2)
(3)当点Q的运动速度是每秒个单位或每秒个单位时,与全等.
5.C
6.(﹣3,0).
7.
8.(1)2;(2)
9.(1)解:设直线l的表达式为y=kx+b,
将(0,1),(2,3)分别代入上式,
得:,
解得:,
∴设直线l的表达式为:y=x+1,
∴当y=0时,x=﹣1,
∴点C的坐标为(﹣1,0);
(2)解:∵,
∴CM=2,
∴点M的坐标为(﹣3,0)或(1,0).
10.B
11.A
12.(1);
(2).
13.C
解:①当x=0时,y=-2,则经过点,正确;
②当y=0时,则-x-2=0,解得:x=-2,即图象与轴的交点坐标是,正确;
③k=-1<0,则y随x的增大而减小,错误;
④图象交y轴负半轴,则图象经过二,三,四象限,不过第一象限,正确;
⑤k值相等,图象平行,正确.
14.A
15.A
16.C
解:,
∵,
∴,故①正确;
当即时,,
解得符合题意;
当即时,,
解得与矛盾,不合题意,故②错误;
当即时,,
解得,
∴不等式的解集是;
当即时,,
解得,
∴不等式的解集是;
综上,不等式的解集为或,故③正确;
当即时,,
当即时,
函数图象如下,当函数图象与直线(m为常数)只有1个交点,则.
所以④正确;
正确的结论有①③④,共三个,
17.A
解:把代入得:,
解得:,
,
把代入得:,
解得:,
直线AB为,
当的对应点在轴负半轴时,过作轴于,如图所示:
在中,令得,
,
,
,
,
设,则,
,
在Rt中,,
,
解得:,
,
设直线EM解析式为,把代入得:,
解得:,
直线EM解析式为.
18.
19.1或2
20.
21.或
解:当y=0时,则x=4,即A(4,0)
当x=0时,则y=3,即B(0,3)
∴OA=4,OB=3
∴
①当点A落在y轴正半轴上时
设点C的坐标为(m,0)
由折叠可得:A'O=3+5=8,A'C=AC=4-m
∵
∴
解得:m=-6
②当点A落在y轴负半轴上时
设点C的坐标为(m,0)
由折叠可得:A'O=5-3=2,A'C=AC=4-m
∵
∴
解得:
综上所示,当点落在轴上时,点的坐标为或
22.(1)解:根据题意,得
,①
,②
由①,得,③
由②③,得.
解得,.
所以该函数的表达式为.
(2)解:因为点在该函数图象上,
所以.
所以.
(3)解:设点的坐标为.
因为直线与轴相交,
所以交点坐标为.
因为
所以.
解得或.
所以点的坐标为或.
23.(1)9
(2)点C的坐标为或
(3)点或
24.(1)
(2)2
(3)点P有两个,坐标为或
1 / 1
知识点1 正比例函数图象
1.已知正比例函数,当时,,则下列各点中在该函数图象上的是( )
A. B. C. D.
2.已知正比例函数的图象过点,则k= .
3.如果正比例函数的图象经过第二、四象限,那么k的取值范围是 .
4.已知:如图点在正比例函数图象上,点B坐标为,连接,,点C是线段的中点,点P在线段上以每秒2个单位的速度由点B向点O运动,点Q在线段上由点A向点O运动,P、Q两点同时运动,同时停止,运动时间为t秒
(1)求该正比例函数的解析式:
(2)当秒,且时,求点Q的坐标:
(3)连接,在点P、Q运动过程中,与是否全等?如果全等,请求出点Q的运动速度;如果不全等,请说明理由
知识点2 一次函数图象
5.已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )
A. B.
C. D.
6.一次函数y=﹣x﹣3与x轴交点的坐标是 .
7.直线的图象如图所示,则代数式的值为 .
8.已知一次函数.
(1)若这个函数的图象经过原点,求a的值.
(2)若这个函数的图象经过一、三、四象限,求a的取值范围.
9.如图,已知直线l经过点A(0,1)与点B(2,3),且与x轴交于点C,点M是x轴上的一点.
(1)求直线l的表达式及点C的坐标;
(2)若△BCM的面积为3,求点M的坐标.
知识点3 一次函数的性质
10.若点,点是一次函数图象上的两个点,则与的大小关系是( )
A. B. C. D.
11.若函数(k为常数,且)中,随的增大而增大,则其图像可能是( )
A. B.
C. D.
12.已知关于的一次函数.
(1)求的值;
(2)当时,求的取值范围.
提高练习
13.关于函数的图象,有如下说法:①图象过点;②图象与轴的交点坐标是;③从图象知随的增大而增大;④图象不过第一象限;⑤图象与函数的图象平行,其中正确的说法有( )
A.2个 B.3个 C.4个 D.5个
14.已知直线上横、纵坐标都是整数的点的个数是
A.0个 B.1个
C.不少于2个但有限个 D.无数个
15.已知与是一次函数.若,那么如图所示的个图中正确的是( )
A. B.
C. D.
16.定义一种新运算:,例如:,,给出下列说法:
①;
②若,则或4;
③的解集为或;
④若函数的图象与直线(m为常数)只有1个交点,则.
以上说法中正确的个数为( )
A.1 B.2 C.3 D.4
17.已知,如图,平面直角坐标系中,直线与坐标轴交于A、B两点,直线与坐标轴交于C、D两点,两直线交于点;点是轴上一动点,连接ME,将沿ME翻折,点对应点刚好落在轴负半轴上,则ME所在直线解析式为( )
A. B. C. D.
18.已知是直线(为常数)上的三个点,则的大小关系是 (用“”表示).
19.若关于x的一次函数的图象经过点和点,当时,,且与y轴相交于正半轴,则整数m的值为 .
20.已知一次函数的图象在y轴上的截距与一次函数的图象在y轴上的截距互为相反数,则 .
21.如图所示,一次函数的图象与轴交于点,与轴交于点,是轴上一动点,连接,将沿所在的直线折叠,当点落在轴上时,点的坐标为 .
22.设一次函数(,为常数,)的图象经过,两点.
(1)求该函数的表达式;
(2)若点在该函数的图象上,求的值;
(3)设点在轴上,若,求点的坐标.
23.如图,直线与x轴相交于点A,与y轴相交于点 B.
(1)直接写出的面积;
(2)若C为y轴上一点,且的面积是,求点C的坐标;
(3)若P是x轴上一点,且,求P的坐标.
24.已知直线与直线.
(1)求两直线交点C的坐标;
(2)求的面积.
(3)在直线上能否找到点P,使得,若能,请求出点P的坐标,若不能请说明理由.
参考答案
1.B
2.
3.
4.(1)
(2)
(3)当点Q的运动速度是每秒个单位或每秒个单位时,与全等.
5.C
6.(﹣3,0).
7.
8.(1)2;(2)
9.(1)解:设直线l的表达式为y=kx+b,
将(0,1),(2,3)分别代入上式,
得:,
解得:,
∴设直线l的表达式为:y=x+1,
∴当y=0时,x=﹣1,
∴点C的坐标为(﹣1,0);
(2)解:∵,
∴CM=2,
∴点M的坐标为(﹣3,0)或(1,0).
10.B
11.A
12.(1);
(2).
13.C
解:①当x=0时,y=-2,则经过点,正确;
②当y=0时,则-x-2=0,解得:x=-2,即图象与轴的交点坐标是,正确;
③k=-1<0,则y随x的增大而减小,错误;
④图象交y轴负半轴,则图象经过二,三,四象限,不过第一象限,正确;
⑤k值相等,图象平行,正确.
14.A
15.A
16.C
解:,
∵,
∴,故①正确;
当即时,,
解得符合题意;
当即时,,
解得与矛盾,不合题意,故②错误;
当即时,,
解得,
∴不等式的解集是;
当即时,,
解得,
∴不等式的解集是;
综上,不等式的解集为或,故③正确;
当即时,,
当即时,
函数图象如下,当函数图象与直线(m为常数)只有1个交点,则.
所以④正确;
正确的结论有①③④,共三个,
17.A
解:把代入得:,
解得:,
,
把代入得:,
解得:,
直线AB为,
当的对应点在轴负半轴时,过作轴于,如图所示:
在中,令得,
,
,
,
,
设,则,
,
在Rt中,,
,
解得:,
,
设直线EM解析式为,把代入得:,
解得:,
直线EM解析式为.
18.
19.1或2
20.
21.或
解:当y=0时,则x=4,即A(4,0)
当x=0时,则y=3,即B(0,3)
∴OA=4,OB=3
∴
①当点A落在y轴正半轴上时
设点C的坐标为(m,0)
由折叠可得:A'O=3+5=8,A'C=AC=4-m
∵
∴
解得:m=-6
②当点A落在y轴负半轴上时
设点C的坐标为(m,0)
由折叠可得:A'O=5-3=2,A'C=AC=4-m
∵
∴
解得:
综上所示,当点落在轴上时,点的坐标为或
22.(1)解:根据题意,得
,①
,②
由①,得,③
由②③,得.
解得,.
所以该函数的表达式为.
(2)解:因为点在该函数图象上,
所以.
所以.
(3)解:设点的坐标为.
因为直线与轴相交,
所以交点坐标为.
因为
所以.
解得或.
所以点的坐标为或.
23.(1)9
(2)点C的坐标为或
(3)点或
24.(1)
(2)2
(3)点P有两个,坐标为或
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
