初中数学浙教版八年级上册 5.5. 一次函数的简单应 用同步练习(含答案)
文档属性
| 名称 | 初中数学浙教版八年级上册 5.5. 一次函数的简单应 用同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 415.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 18:06:49 | ||
图片预览


文档简介
5.5. 一次函数的简单应用
知识点1 建立一次函数模型
1.小明同学在一次学科综合实践活动中发现,某品牌鞋子的长度与鞋子的码数之间满足一次函数关系,下表给出与的一些对应值:根据小明的数据,可以得出该品牌38码鞋子的长度为( )
码数x 26 30 34 42
长度y 18 20 22 26
A. B. C. D.
2.某商店销售A,B两种型号智能手表,这两种手表的进价和售价如下表:
型号 A B
进价(元/只) 1200 2000
售价(元/只) 1800 2500
该商场购进A,B两种型号智能手表共60只.
(1)若该商场计划用8.4万元购进A,B两种型号智能手表,求购进A,B两种型号智能手表各多少只?
(2)若该商店用于购进智能手表的资金不超过8.8万元,且A型号的智能手表不得超过44只.若这两种智能手表都按售价全部售完,那么该商店应如何进货,才能使得获利最大,最大利润是多少?
知识点2 实际问题中的分段函数
3.已知小强家、体育馆、文具店在同一直线上如图中的图象反映的过程是:小强从家跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后散步回家.下列信息中正确的是( )
A.小强在体育馆花了20分钟锻炼
B.小强从家跑步去体育场的速度是10km/h
C.体育馆与文具店的距离是3km
D.小强从文具店散步回家用了90分钟
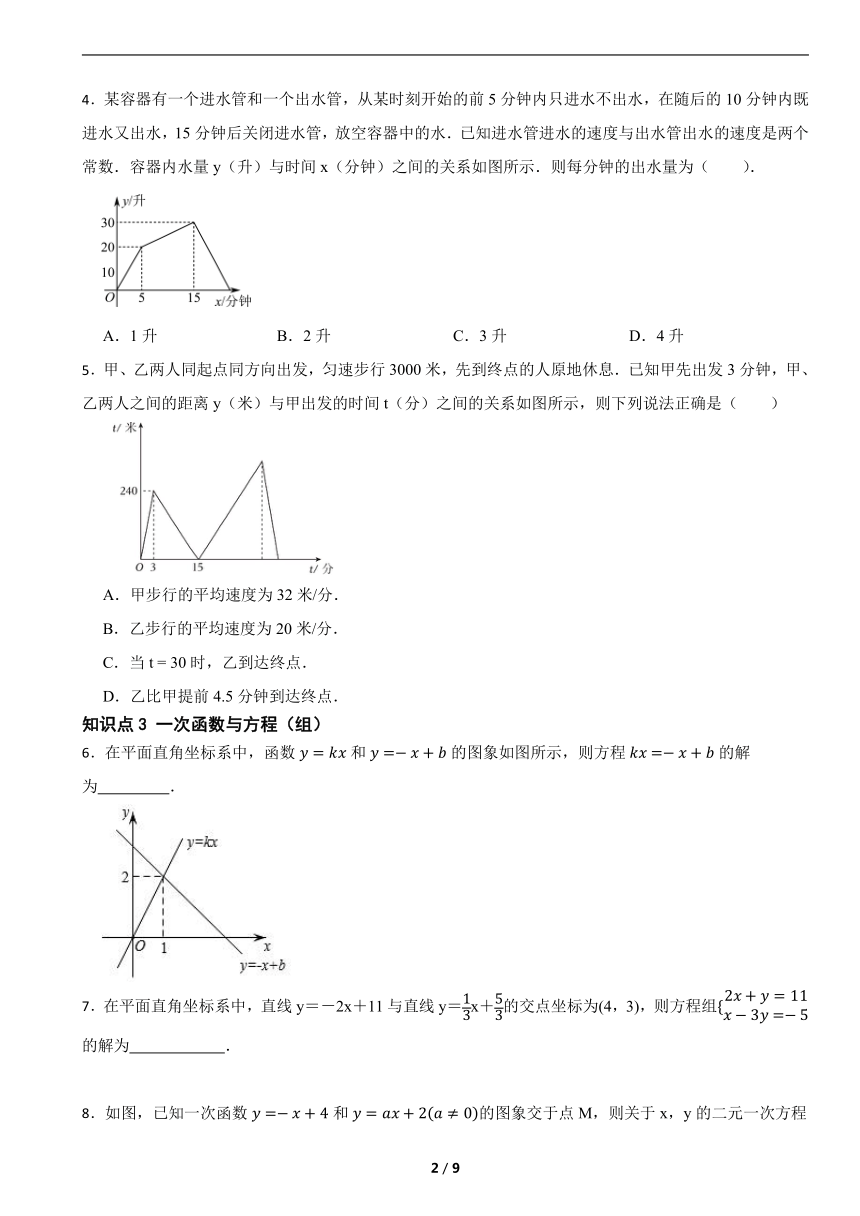
4.某容器有一个进水管和一个出水管,从某时刻开始的前5分钟内只进水不出水,在随后的10分钟内既进水又出水,15分钟后关闭进水管,放空容器中的水.已知进水管进水的速度与出水管出水的速度是两个常数.容器内水量y(升)与时间x(分钟)之间的关系如图所示.则每分钟的出水量为( ).
A.1升 B.2升 C.3升 D.4升
5.甲、乙两人同起点同方向出发,匀速步行3000米,先到终点的人原地休息.已知甲先出发3分钟,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则下列说法正确是( )
A.甲步行的平均速度为32米/分.
B.乙步行的平均速度为20米/分.
C.当t = 30时,乙到达终点.
D.乙比甲提前4.5分钟到达终点.
知识点3 一次函数与方程(组)
6.在平面直角坐标系中,函数和的图象如图所示,则方程的解为 .
7.在平面直角坐标系中,直线y=-2x+11与直线y=x+的交点坐标为(4,3),则方程组的解为 .
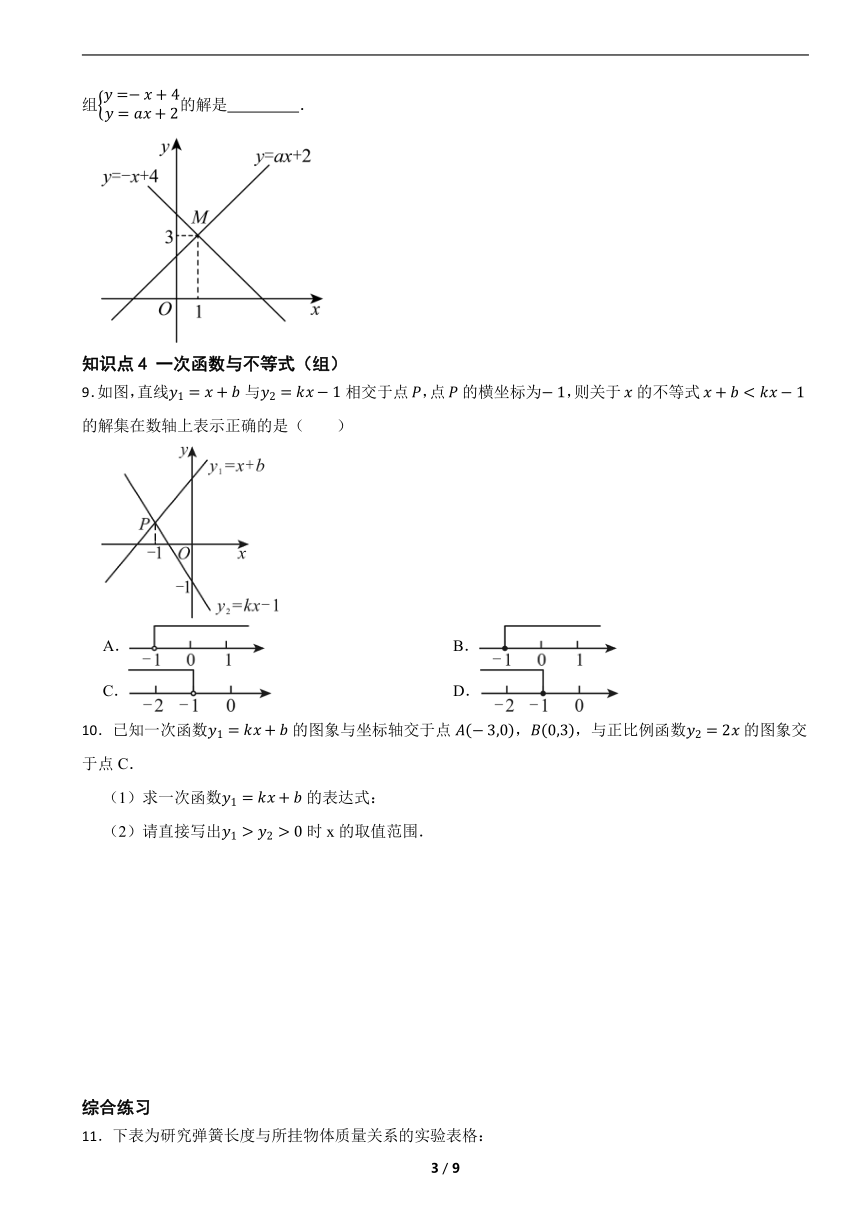
8.如图,已知一次函数和的图象交于点M,则关于x,y的二元一次方程组的解是 .
知识点4 一次函数与不等式(组)
9.如图,直线与相交于点,点的横坐标为,则关于的不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
10.已知一次函数的图象与坐标轴交于点,,与正比例函数的图象交于点C.
(1)求一次函数的表达式:
(2)请直接写出时x的取值范围.
综合练习
11.下表为研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量 2 3 4 5
弹簧长度 12 14 16 18
则弹簧不挂物体时的长度为( )
A. B. C. D.
12.如图,一次函数与的图象相交于点A,则点A的坐标为( )
A. B. C. D.
13.初二年级在小学段期间外出游学,同学们所乘的客车先在公路上匀速行驶,在服务区休息一段时间后,进入高速路继续匀速行驶,已知客车行驶的路程s(千米)与行驶的时间r(小时)的函数关系的图象如图所示,则客车在高速路上行驶的速度为( )
A.60千米/小时 B.75千米/小时
C.80千米/小时 D.90千米/小时
14.某品牌自动饮水机,开机加热时每分钟上升,加热到,停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中正确的是( )
A.上午点接通电源,可以保证当天能喝到不超过的水
B.水温下降过程中,与的函数关系式是
C.水温从加热到,需要
D.水温不低于的时间为
15.一次函数、为常数且,与的图象相交于点,则关于的方程的解为 .
16.匀速行驶的一列火车穿过一个随道,车在隧道内长度与火车行驶时间之间的关系可用如图所示的图象描述,则该隧道的长度等于 m.
17.已知函数y=kx+b,其中x与y的部分对应值如下表,则关于x的不等式kx+b<0的解是 .
x -1 0 1 2
y 4 2 0 -2
18.在直角坐标系内,一次函数.与y的图象如图所示,则关于x,y的方程组的解是 .
19.如图,直线与的交点的横坐标为.下列结论:①,;②直线一定经过点;③m与n满足;④当时,.其中正确的有 .(只填序号)
20.如图所示为一种吸水拖把,它由吸水部分、拉手部分和主干部分构成.小明在拖地中发现,拉手部分在一拉一放的过程中,吸水部分弯曲的角度会发生变化.设拉手部分移动的距离为吸水部分弯曲所成的角度为,经测量发现:拉手部分每移动,吸水部分角度变化.请回答下列问题:
(1)求出关于的函数解析式;
(2)当吸水部分弯曲所成的角度为时,求拉手部分移动的距离.
21.如图,在平面直角坐标系中,放置一平面镜,其中点,的坐标分别为,,从点发射光线,其图象对应的函数表达式为(,).
(1)点为平面镜的中点,若光线恰好经过点,求所在直线的表达式;
(2)若入射光线(,)与平面镜有公共点,求的取值范围;
22.如图,函数y=2x与y=ax+5的图象相交于点A(m,4).
(1)求A点坐标及一次函数y=ax+5的解析式;
(2)设直线y=ax+5与x轴交于点B,求的面积;
(3)不等式2x<ax+5的解集为 .
23.如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点,且点的坐标为.
(1)则_________,_________;
(2)关于的不等式的解集是_________;
(3)四边形的面积_________;
(4)在平面内是否存在点,使得以点为顶点的三角形是以为腰的等腰直角三角形,若存在,请直接写出点的坐标;若不存在,请说明理由.
参考答案
1.A
2.(1)A型45只,B型15只.
(2)A型44只,B型16只获利最大:最大利润是34400元
3.B
4.C
5.D
解:A、根据图象可得,甲的速度为240÷3=80(米/分),∴A不符合题意;
B、设乙的速度为x米/分,根据图象可得,(15 3)x=240+80×(15 3),解得x=100,∴乙的速度为100米/分,∴B不符合题
意;
C、∵甲到达终点的时间为3000÷80=37.5(分钟),乙达到终点的时间为3000÷100=30(分钟),30+3=33(分钟),∴当t=33时,乙到达终点,∴C不符合题意;
D、∵甲先出发3分钟,∴乙先到终点原地休息了37.5 3 30=4.5(分钟),∴乙比甲提前4.5分钟到达终点,∴D符合题意.
6.
7.
,直线y=-2x+11与直线y=x+的交点坐标为(4,3),
方程组的解为 ,
8.
9.C
10.(1)
(2)
11.B
12.C
13.C
14.D
15.-2
解: 为两个函数图形的交点,
把N (m,-6)代入y=3x得:3m=-6,解得m=-2,
N(-2,-6),
关于x的方程kx-b=3x的解即为交点的横坐标,即x=-2,
16.900
解:根据题意可得,
火车的速度为:150÷(35 30)=30m/s,
∴隧道的长度为:30×30=900m,
17.x>1
解:根据题意可得,k<0,即y随x的增大而减小,
∵ x=1时,y=0,
∴ kx+b<0的解为x>1.
18.
解:观察图象可得,的解为
19.①②③
20.(1);(2)拉手部分移动的距离为或.
21.(1)
(2)
22.(1)(2,4),y=﹣x+5;(2)20;(3)x<2
23.(1)3,
(2)
(3)
(4),,,
1 / 1
知识点1 建立一次函数模型
1.小明同学在一次学科综合实践活动中发现,某品牌鞋子的长度与鞋子的码数之间满足一次函数关系,下表给出与的一些对应值:根据小明的数据,可以得出该品牌38码鞋子的长度为( )
码数x 26 30 34 42
长度y 18 20 22 26
A. B. C. D.
2.某商店销售A,B两种型号智能手表,这两种手表的进价和售价如下表:
型号 A B
进价(元/只) 1200 2000
售价(元/只) 1800 2500
该商场购进A,B两种型号智能手表共60只.
(1)若该商场计划用8.4万元购进A,B两种型号智能手表,求购进A,B两种型号智能手表各多少只?
(2)若该商店用于购进智能手表的资金不超过8.8万元,且A型号的智能手表不得超过44只.若这两种智能手表都按售价全部售完,那么该商店应如何进货,才能使得获利最大,最大利润是多少?
知识点2 实际问题中的分段函数
3.已知小强家、体育馆、文具店在同一直线上如图中的图象反映的过程是:小强从家跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后散步回家.下列信息中正确的是( )
A.小强在体育馆花了20分钟锻炼
B.小强从家跑步去体育场的速度是10km/h
C.体育馆与文具店的距离是3km
D.小强从文具店散步回家用了90分钟
4.某容器有一个进水管和一个出水管,从某时刻开始的前5分钟内只进水不出水,在随后的10分钟内既进水又出水,15分钟后关闭进水管,放空容器中的水.已知进水管进水的速度与出水管出水的速度是两个常数.容器内水量y(升)与时间x(分钟)之间的关系如图所示.则每分钟的出水量为( ).
A.1升 B.2升 C.3升 D.4升
5.甲、乙两人同起点同方向出发,匀速步行3000米,先到终点的人原地休息.已知甲先出发3分钟,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则下列说法正确是( )
A.甲步行的平均速度为32米/分.
B.乙步行的平均速度为20米/分.
C.当t = 30时,乙到达终点.
D.乙比甲提前4.5分钟到达终点.
知识点3 一次函数与方程(组)
6.在平面直角坐标系中,函数和的图象如图所示,则方程的解为 .
7.在平面直角坐标系中,直线y=-2x+11与直线y=x+的交点坐标为(4,3),则方程组的解为 .
8.如图,已知一次函数和的图象交于点M,则关于x,y的二元一次方程组的解是 .
知识点4 一次函数与不等式(组)
9.如图,直线与相交于点,点的横坐标为,则关于的不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
10.已知一次函数的图象与坐标轴交于点,,与正比例函数的图象交于点C.
(1)求一次函数的表达式:
(2)请直接写出时x的取值范围.
综合练习
11.下表为研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量 2 3 4 5
弹簧长度 12 14 16 18
则弹簧不挂物体时的长度为( )
A. B. C. D.
12.如图,一次函数与的图象相交于点A,则点A的坐标为( )
A. B. C. D.
13.初二年级在小学段期间外出游学,同学们所乘的客车先在公路上匀速行驶,在服务区休息一段时间后,进入高速路继续匀速行驶,已知客车行驶的路程s(千米)与行驶的时间r(小时)的函数关系的图象如图所示,则客车在高速路上行驶的速度为( )
A.60千米/小时 B.75千米/小时
C.80千米/小时 D.90千米/小时
14.某品牌自动饮水机,开机加热时每分钟上升,加热到,停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中正确的是( )
A.上午点接通电源,可以保证当天能喝到不超过的水
B.水温下降过程中,与的函数关系式是
C.水温从加热到,需要
D.水温不低于的时间为
15.一次函数、为常数且,与的图象相交于点,则关于的方程的解为 .
16.匀速行驶的一列火车穿过一个随道,车在隧道内长度与火车行驶时间之间的关系可用如图所示的图象描述,则该隧道的长度等于 m.
17.已知函数y=kx+b,其中x与y的部分对应值如下表,则关于x的不等式kx+b<0的解是 .
x -1 0 1 2
y 4 2 0 -2
18.在直角坐标系内,一次函数.与y的图象如图所示,则关于x,y的方程组的解是 .
19.如图,直线与的交点的横坐标为.下列结论:①,;②直线一定经过点;③m与n满足;④当时,.其中正确的有 .(只填序号)
20.如图所示为一种吸水拖把,它由吸水部分、拉手部分和主干部分构成.小明在拖地中发现,拉手部分在一拉一放的过程中,吸水部分弯曲的角度会发生变化.设拉手部分移动的距离为吸水部分弯曲所成的角度为,经测量发现:拉手部分每移动,吸水部分角度变化.请回答下列问题:
(1)求出关于的函数解析式;
(2)当吸水部分弯曲所成的角度为时,求拉手部分移动的距离.
21.如图,在平面直角坐标系中,放置一平面镜,其中点,的坐标分别为,,从点发射光线,其图象对应的函数表达式为(,).
(1)点为平面镜的中点,若光线恰好经过点,求所在直线的表达式;
(2)若入射光线(,)与平面镜有公共点,求的取值范围;
22.如图,函数y=2x与y=ax+5的图象相交于点A(m,4).
(1)求A点坐标及一次函数y=ax+5的解析式;
(2)设直线y=ax+5与x轴交于点B,求的面积;
(3)不等式2x<ax+5的解集为 .
23.如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点,且点的坐标为.
(1)则_________,_________;
(2)关于的不等式的解集是_________;
(3)四边形的面积_________;
(4)在平面内是否存在点,使得以点为顶点的三角形是以为腰的等腰直角三角形,若存在,请直接写出点的坐标;若不存在,请说明理由.
参考答案
1.A
2.(1)A型45只,B型15只.
(2)A型44只,B型16只获利最大:最大利润是34400元
3.B
4.C
5.D
解:A、根据图象可得,甲的速度为240÷3=80(米/分),∴A不符合题意;
B、设乙的速度为x米/分,根据图象可得,(15 3)x=240+80×(15 3),解得x=100,∴乙的速度为100米/分,∴B不符合题
意;
C、∵甲到达终点的时间为3000÷80=37.5(分钟),乙达到终点的时间为3000÷100=30(分钟),30+3=33(分钟),∴当t=33时,乙到达终点,∴C不符合题意;
D、∵甲先出发3分钟,∴乙先到终点原地休息了37.5 3 30=4.5(分钟),∴乙比甲提前4.5分钟到达终点,∴D符合题意.
6.
7.
,直线y=-2x+11与直线y=x+的交点坐标为(4,3),
方程组的解为 ,
8.
9.C
10.(1)
(2)
11.B
12.C
13.C
14.D
15.-2
解: 为两个函数图形的交点,
把N (m,-6)代入y=3x得:3m=-6,解得m=-2,
N(-2,-6),
关于x的方程kx-b=3x的解即为交点的横坐标,即x=-2,
16.900
解:根据题意可得,
火车的速度为:150÷(35 30)=30m/s,
∴隧道的长度为:30×30=900m,
17.x>1
解:根据题意可得,k<0,即y随x的增大而减小,
∵ x=1时,y=0,
∴ kx+b<0的解为x>1.
18.
解:观察图象可得,的解为
19.①②③
20.(1);(2)拉手部分移动的距离为或.
21.(1)
(2)
22.(1)(2,4),y=﹣x+5;(2)20;(3)x<2
23.(1)3,
(2)
(3)
(4),,,
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
