6.7角的和差 课件（共21张PPT）

(共21张PPT)
6.7 角的和差
浙教版七年级上册
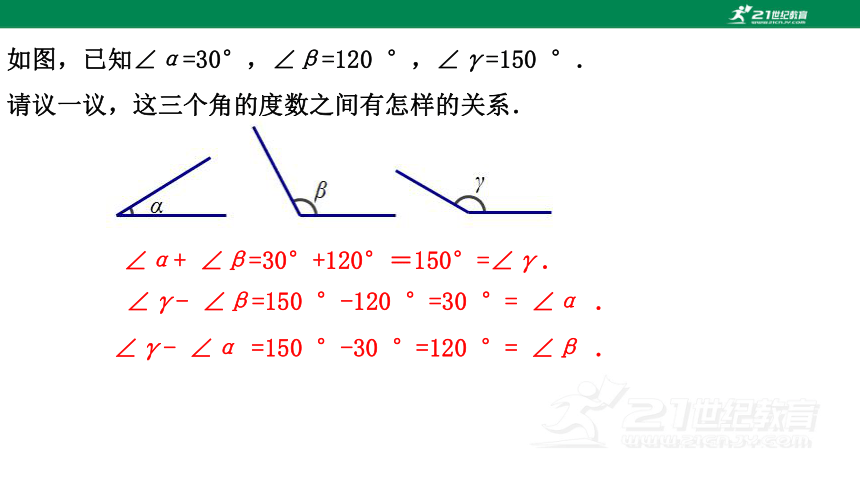
如图，已知∠α=30°，∠β=120 °，∠γ=150 °．
请议一议，这三个角的度数之间有怎样的关系．
∠α+ ∠β=30°+120°＝150°=∠γ．
∠γ- ∠β=150 °-120 °=30 °= ∠α ．
∠γ- ∠α =150 °-30 °=120 °= ∠β ．
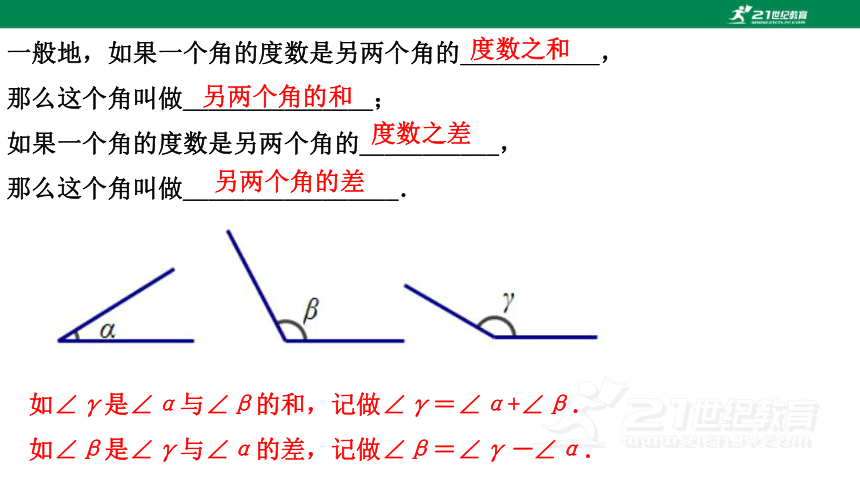
一般地，如果一个角的度数是另两个角的___________，
那么这个角叫做_______________；
如果一个角的度数是另两个角的___________，
那么这个角叫做_________________．
度数之和
另两个角的和
度数之差
另两个角的差
如∠γ是∠α与∠β的和，记做∠γ＝∠α+∠β．
如∠β是∠γ与∠α的差，记做∠β＝∠γ－∠α．
同一端点的三条射线如图，请完成下面的填空：
∠AOB+∠BOC=∠________=________度；
∠ AOC-∠BOC= ∠ ________=________度；
∠BOC= ∠ AOC-∠ ________=________度．
AOC
110
AOB
30
AOB
80
两个角可以相加(或相减)，它们的和(或差)也是一个角．
它的度数等于这两个角的度数的和(或差).
21世纪教育网
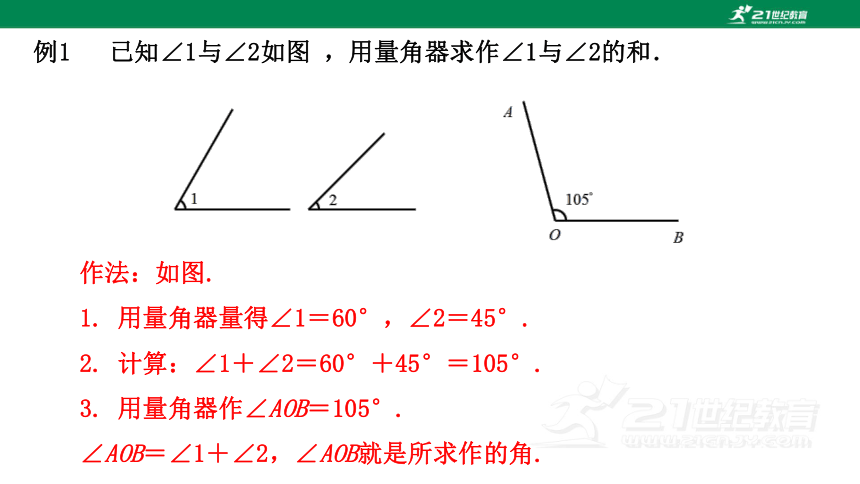
例1 　已知∠1与∠2如图 ，用量角器求作∠1与∠2的和．
作法：如图.
1. 用量角器量得∠1＝60°，∠2＝45°.
2. 计算：∠1＋∠2＝60°＋45°＝105°.
3. 用量角器作∠AOB＝105°.
∠AOB＝∠1＋∠2，∠AOB就是所求作的角.
从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线．
当∠1 =∠2 时，射线OC把∠AOB分成两个相等的角，
这时OC叫做∠AOB的平分线，也可以说OC平分∠AOB．
O
B
A
C
1
2
几何语言：
∵OC是∠AOB的平分线，
∴ ∠AOC=∠BOC，
∠AOC=∠BOC= ∠AOB，
∠AOB=2 ∠AOC=2∠BOC．
∵∠AOC=∠BOC，
∠AOC=∠BOC= ∠AOB，
∠AOB=2 ∠AOC=2∠BOC．
∴ OC是∠AOB的平分线．
反之：
在一张透明纸上任意画一个角∠AOB，把这张纸折叠，
使角的两边OA与OB重合，然后把纸展开，画出折痕OC．
问∠AOC与∠BOC之间有怎样的大小关系？
∵折叠时∠AOC与∠BOC重合，
∴ ∠AOC=∠BOC=∠AOB．
折叠出等角
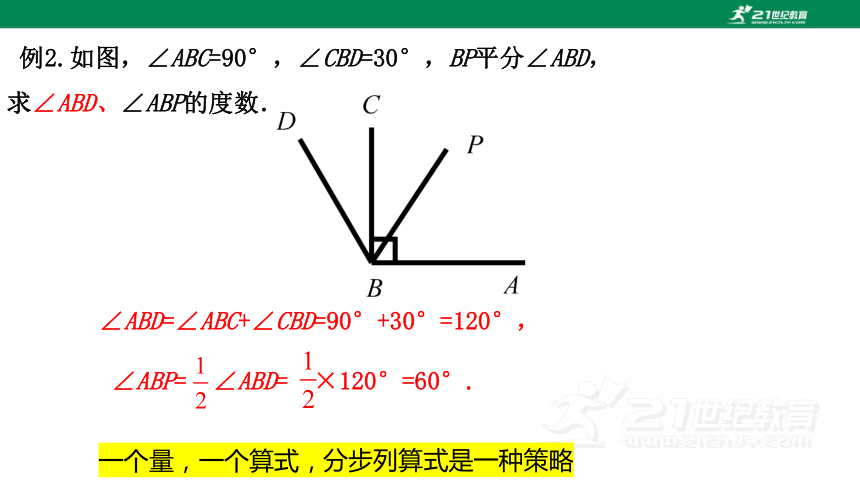
例2.如图，∠ABC=90°，∠CBD=30°，BP平分∠ABD，
求∠ABD、∠ABP的度数．
∠ABD=∠ABC+∠CBD=90°+30°=120°，
∠ABP= ∠ABD= ×120°=60°.
一个量，一个算式，
分步列算式是一种策略
一个角，一个算术表达，
分步列算式是一种策略
一个角，一个代数表达，
分步列代数式是一种策略
1.如图，点O为直线AB上一点，∠COB＝28°，求∠1的度数
∠1＝180°－∠COB＝180°－28°＝152°.
夯实基础，稳扎稳打
2.如图，已知∠AOC＝∠BOD＝80°，∠BOC＝25°，
求∠AOB、∠COD、∠AOD的度数
∠COD＝∠BOD－∠BOC＝80°－25°＝55°，
∠AOD＝∠AOB＋∠BOD＝80°＋55°＝135°，
∠AOB＝∠AOC－∠BOC＝80°－25°＝55°，
∠AOD＝∠COD＋∠AOC＝80°＋55°＝135°，
25°
80°
80°
标记度数
3.把一张长方形纸条按如图所示的方式折叠后，量得∠AOB′＝110°，
求∠B′OB、∠B′OC 的度数
∠B′OB=∠AOB - ∠AOB′=180°-110°=70°
∠B′OC=∠B′OB=
110°
标记度数
4.如图，将一张长方形纸片沿线段AB折叠，已知∠1＝65°，求∠2的度数
∠3＝∠1＝65°，
∠2＝180°－∠3－∠1＝180°－2×65°＝50°.
65°
5.已知正方形的每个角等于90°，请解决下列问题：
将两个正方形的一个顶点O重合放置，
若∠AOD＝40°，求∠AOC、∠COB的度数.
∠AOC=∠COD∠AOD＝90°0°，
∠COB＝∠AOC＋∠AOB＝90°0°=140°.
∠BOD=∠AO∠AOD＝90°0°，
∠COB＝∠COD＋∠BOD＝90°0°=140°.
40°
∟
∟
标记符号
6.如图，点C，O，D在同一条直线上，∠AOC＝40°，∠BOD＝50°，
OM，ON分别是∠AOC，∠BOD的平分线，
求∠AOB、∠MOA、∠NOB、∠MON的度数.
∠AOB＝∠COD∠AOC∠BOD＝180°40°0°=90°，
∠MON＝∠MOA＋∠AOB＋∠NOB＝135°.
40°
50°
7.如图，点O在直线AB上，∠1∶∠2∶∠3＝1∶3∶2，求∠DOB 的度数
∠1=k°，∠2＝3k°，∠3＝2k°，
k°＋3k°＋2k°＝180°，k＝30，
∠DOB＝k°＋3k°＝120°.
逢比就设
k
3k
2k
x
x
y
y
x+x+y+y=180
∠GEF=x+y＝90°，
连续递推，豁然开朗
9.如图，将长方形纸片进行折叠，ED，EF为折痕，A与A′，B与B′，C与C′重合，，求∠DEF的度数
∠DEF=x+y＝90°，
x
x
y
y
x+x+y+y=180
给你一张直角三角形纸片，你能通过折叠的方法再折出一个直角来吗？你还能把这张纸片折成一个长方形吗？
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin