浙教版七年级数学上册第五章 一元一次方程练习(含答案)
文档属性
| 名称 | 浙教版七年级数学上册第五章 一元一次方程练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 58.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 14:24:03 | ||
图片预览



文档简介
第五章 一元一次方程 练习
一、选择题
1.下列各式中,是一元一次方程的是( )
A.x2+1=5 B.3-2x=5 C.3x+y=3 D.2x-1
2.下列运用等式的性质对等式进行的变形中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
3.解方程时,去括号正确的是( )
A. B. C. D.
4.已知x=1是方程x+2a=-1的解,那么a的值是( )
A.-1 B.0 C.1 D.2
5.若代数式3a+1的值与3(a+1)的值互为相反数,则a的值为( )
A. B. C. D.
6.元朝朱世杰所著的算学启蒙中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行里,慢马每天行里,慢马先行天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )
A. B.
C. D.
7.若关于x的一元二次方程的解为,那么关于y的一元一次方程的解为( )
A. B. C. D.
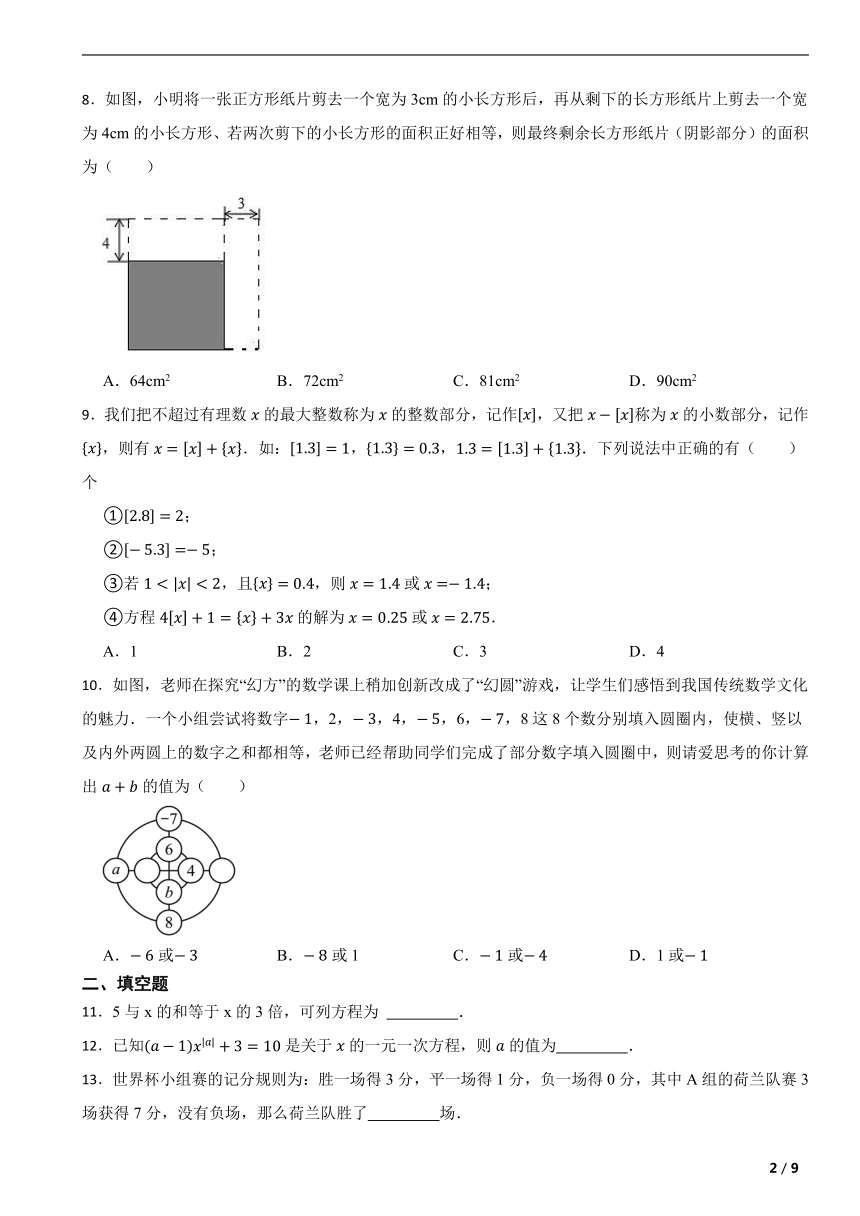
8.如图,小明将一张正方形纸片剪去一个宽为3cm的小长方形后,再从剩下的长方形纸片上剪去一个宽为4cm的小长方形、若两次剪下的小长方形的面积正好相等,则最终剩余长方形纸片(阴影部分)的面积为( )
A.64cm2 B.72cm2 C.81cm2 D.90cm2
9.我们把不超过有理数的最大整数称为的整数部分,记作,又把称为的小数部分,记作,则有.如:,,.下列说法中正确的有( )个
①;
②;
③若,且,则或;
④方程的解为或.
A.1 B.2 C.3 D.4
10.如图,老师在探究“幻方”的数学课上稍加创新改成了“幻圆”游戏,让学生们感悟到我国传统数学文化的魅力.一个小组尝试将数字,2,,4,,6,,8这8个数分别填入圆圈内,使横、竖以及内外两圆上的数字之和都相等,老师已经帮助同学们完成了部分数字填入圆圈中,则请爱思考的你计算出的值为( )
A.或 B.或1 C.或 D.1或
二、填空题
11.5与x的和等于x的3倍,可列方程为 .
12.已知是关于的一元一次方程,则的值为 .
13.世界杯小组赛的记分规则为:胜一场得3分,平一场得1分,负一场得0分,其中A组的荷兰队赛3场获得7分,没有负场,那么荷兰队胜了 场.
14.定义a*b=ab+a+b,若3*x=27,则x的值是 。
15.如果关于x的方程(a-4)x=-2无解,那么实数a= .
16.如图已知数轴有A、B两点,分别表示的数为、18.点P沿线段自点A向点B以2个单位/秒的速度运动,点P出发3秒后,点Q沿线段自点B向A以4个单位/秒的速度运动,问再经过 秒P,Q两点相距8个单位长度.
三、解答题
17.解方程:
(1);
(2) .
18.已知x=3 是方程 的解,求m的值.
19.观察下列两列数:
、……①
、……②
(1)第①行第10个数是______,第②行第10个数是______;
(2)在第②行中,是否存在三个连续数,其和为83?若存在,求出这三个数;若不存在,说明理由.
20.小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是2x﹣█=x+1.
(1)小明猜想“█”部分是2.请你算一算x的值;
(2)小明翻看了书后的答案,发现此方程的解与方程1﹣=的解相同,请你算一算被污染的常数应是多少?
21.根据绝对值的意义,若|x|=3,则x=±3,若|y|=a,则y=±a,
我们可以根据这样的结论,解一些简单的绝对值方程,如:
解方程:|x-2|=1.
解:方程可化为x-2=1或x-2=-1,∴x=3或x=1.
请根据以上的解法,解方程:3|x-1|-2=7.
22.已知方程 是关于 x 的一元一次方程.
(1)当方程有解时,求k的取值范围.
(2)当k取什么整数值时,方程的解为正整数
23.根据以下素材,探索完成任务.
素材1 某校统一安装了日光灯,日光灯中最易损坏的是灯管和镇流器.
素材2 该校后勤部准备补进灯管和镇流器共400件.批发市场灯管的单价为30元,镇流器的单价为80元.商家为了促销且保证有一定的利润,当镇流器购买数量超过80件时,每多购买1件,单价下降1元,但单价不低于50元,若低于50元时按50元算.
问题解决
任务1 若镇流器补进90件,则学校补进镇流器和灯管共多少元?
任务2 设镇流器补进x件,若,刚补进镇流器的单价为元,补进灯管的总价为(用含x的代数式表示);
任务3 若学校后勤部补进镇流器和灯管共花15000元,求补进镇流器多少件?
参考答案
1.B
2.B
3.D
4.A
5.A
6.D
7.D
8.B
9.A
10.A
11.
12.
13.2
14.6
解:由题意得:3*x=27可化为3x+3+x=27,
解得x=6,
15.4
∵方程(a-4)x=-2无解,
∴a-4=0,
解得:a=4.
16.或
解:根据题意可知:,点P出发3秒运动的路程为:,
设再经过x秒P,Q两点相距8个单位长度,
两个点相遇前相距8个单位长度,则,
解得:;
两个点相遇后相距8个单位长度,则,
解得:;
综上:再经过秒或秒P,Q两点相距8个单位长度.
17.(1)
(2)
18.解:∵x=3是方程 的解,
∴解得
19.(1);
(2)存在,这三个数分别为85,,89
20.(1)x=2;(2)被污染的常数应是
21.解:3|x-1|=7+2,
移项,得3|x-1|=9,
系数化为”1“,得|x-1|=3
∴方程可化为x-1=3或x-1=-3,
①解x-1=3
得x=4
②解x-1=-3,
得x=-2.
∴x=4或x=-2
22.(1)解:方程两边同乘6:
x-4-2(kx-1)=2
∴x-4-2kx+2=2
∴(1-2k)x=4
∵方程有解
∴1-2k≠0
∴k≠
(2)解:由(1)可得
x=
∵x为正整数
∴(1-2k)能被4整除且为正整数
∴1-2k=1或2或4
∴k=0
23.解:任务1:依题意,镇流器补进90件,
学校补进镇流器和灯管共[80-(90-80)×1]×90+(400-90)×30=15600元,
答:若镇流器补进90件,则学校补进镇流器和灯管共15600元;
任务2:设镇流器补进件,若,
刚补进镇流器的单价为(元),
补进灯管的总价为:(元);
务任务3:当时,依题意,得,解得:;
当时,依题意,得,
解得:(不合题意,舍去),,∴;
当时,镇流器的单价固定为50元,
依题意,得,解得:.
答:补进镇流器60件或100件或150件.
1 / 1
一、选择题
1.下列各式中,是一元一次方程的是( )
A.x2+1=5 B.3-2x=5 C.3x+y=3 D.2x-1
2.下列运用等式的性质对等式进行的变形中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
3.解方程时,去括号正确的是( )
A. B. C. D.
4.已知x=1是方程x+2a=-1的解,那么a的值是( )
A.-1 B.0 C.1 D.2
5.若代数式3a+1的值与3(a+1)的值互为相反数,则a的值为( )
A. B. C. D.
6.元朝朱世杰所著的算学启蒙中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行里,慢马每天行里,慢马先行天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )
A. B.
C. D.
7.若关于x的一元二次方程的解为,那么关于y的一元一次方程的解为( )
A. B. C. D.
8.如图,小明将一张正方形纸片剪去一个宽为3cm的小长方形后,再从剩下的长方形纸片上剪去一个宽为4cm的小长方形、若两次剪下的小长方形的面积正好相等,则最终剩余长方形纸片(阴影部分)的面积为( )
A.64cm2 B.72cm2 C.81cm2 D.90cm2
9.我们把不超过有理数的最大整数称为的整数部分,记作,又把称为的小数部分,记作,则有.如:,,.下列说法中正确的有( )个
①;
②;
③若,且,则或;
④方程的解为或.
A.1 B.2 C.3 D.4
10.如图,老师在探究“幻方”的数学课上稍加创新改成了“幻圆”游戏,让学生们感悟到我国传统数学文化的魅力.一个小组尝试将数字,2,,4,,6,,8这8个数分别填入圆圈内,使横、竖以及内外两圆上的数字之和都相等,老师已经帮助同学们完成了部分数字填入圆圈中,则请爱思考的你计算出的值为( )
A.或 B.或1 C.或 D.1或
二、填空题
11.5与x的和等于x的3倍,可列方程为 .
12.已知是关于的一元一次方程,则的值为 .
13.世界杯小组赛的记分规则为:胜一场得3分,平一场得1分,负一场得0分,其中A组的荷兰队赛3场获得7分,没有负场,那么荷兰队胜了 场.
14.定义a*b=ab+a+b,若3*x=27,则x的值是 。
15.如果关于x的方程(a-4)x=-2无解,那么实数a= .
16.如图已知数轴有A、B两点,分别表示的数为、18.点P沿线段自点A向点B以2个单位/秒的速度运动,点P出发3秒后,点Q沿线段自点B向A以4个单位/秒的速度运动,问再经过 秒P,Q两点相距8个单位长度.
三、解答题
17.解方程:
(1);
(2) .
18.已知x=3 是方程 的解,求m的值.
19.观察下列两列数:
、……①
、……②
(1)第①行第10个数是______,第②行第10个数是______;
(2)在第②行中,是否存在三个连续数,其和为83?若存在,求出这三个数;若不存在,说明理由.
20.小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是2x﹣█=x+1.
(1)小明猜想“█”部分是2.请你算一算x的值;
(2)小明翻看了书后的答案,发现此方程的解与方程1﹣=的解相同,请你算一算被污染的常数应是多少?
21.根据绝对值的意义,若|x|=3,则x=±3,若|y|=a,则y=±a,
我们可以根据这样的结论,解一些简单的绝对值方程,如:
解方程:|x-2|=1.
解:方程可化为x-2=1或x-2=-1,∴x=3或x=1.
请根据以上的解法,解方程:3|x-1|-2=7.
22.已知方程 是关于 x 的一元一次方程.
(1)当方程有解时,求k的取值范围.
(2)当k取什么整数值时,方程的解为正整数
23.根据以下素材,探索完成任务.
素材1 某校统一安装了日光灯,日光灯中最易损坏的是灯管和镇流器.
素材2 该校后勤部准备补进灯管和镇流器共400件.批发市场灯管的单价为30元,镇流器的单价为80元.商家为了促销且保证有一定的利润,当镇流器购买数量超过80件时,每多购买1件,单价下降1元,但单价不低于50元,若低于50元时按50元算.
问题解决
任务1 若镇流器补进90件,则学校补进镇流器和灯管共多少元?
任务2 设镇流器补进x件,若,刚补进镇流器的单价为元,补进灯管的总价为(用含x的代数式表示);
任务3 若学校后勤部补进镇流器和灯管共花15000元,求补进镇流器多少件?
参考答案
1.B
2.B
3.D
4.A
5.A
6.D
7.D
8.B
9.A
10.A
11.
12.
13.2
14.6
解:由题意得:3*x=27可化为3x+3+x=27,
解得x=6,
15.4
∵方程(a-4)x=-2无解,
∴a-4=0,
解得:a=4.
16.或
解:根据题意可知:,点P出发3秒运动的路程为:,
设再经过x秒P,Q两点相距8个单位长度,
两个点相遇前相距8个单位长度,则,
解得:;
两个点相遇后相距8个单位长度,则,
解得:;
综上:再经过秒或秒P,Q两点相距8个单位长度.
17.(1)
(2)
18.解:∵x=3是方程 的解,
∴解得
19.(1);
(2)存在,这三个数分别为85,,89
20.(1)x=2;(2)被污染的常数应是
21.解:3|x-1|=7+2,
移项,得3|x-1|=9,
系数化为”1“,得|x-1|=3
∴方程可化为x-1=3或x-1=-3,
①解x-1=3
得x=4
②解x-1=-3,
得x=-2.
∴x=4或x=-2
22.(1)解:方程两边同乘6:
x-4-2(kx-1)=2
∴x-4-2kx+2=2
∴(1-2k)x=4
∵方程有解
∴1-2k≠0
∴k≠
(2)解:由(1)可得
x=
∵x为正整数
∴(1-2k)能被4整除且为正整数
∴1-2k=1或2或4
∴k=0
23.解:任务1:依题意,镇流器补进90件,
学校补进镇流器和灯管共[80-(90-80)×1]×90+(400-90)×30=15600元,
答:若镇流器补进90件,则学校补进镇流器和灯管共15600元;
任务2:设镇流器补进件,若,
刚补进镇流器的单价为(元),
补进灯管的总价为:(元);
务任务3:当时,依题意,得,解得:;
当时,依题意,得,
解得:(不合题意,舍去),,∴;
当时,镇流器的单价固定为50元,
依题意,得,解得:.
答:补进镇流器60件或100件或150件.
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
