6.8余角和补角 课件（共23张PPT）

(共23张PPT)
6.8 余角和补角
浙教版七年级上册
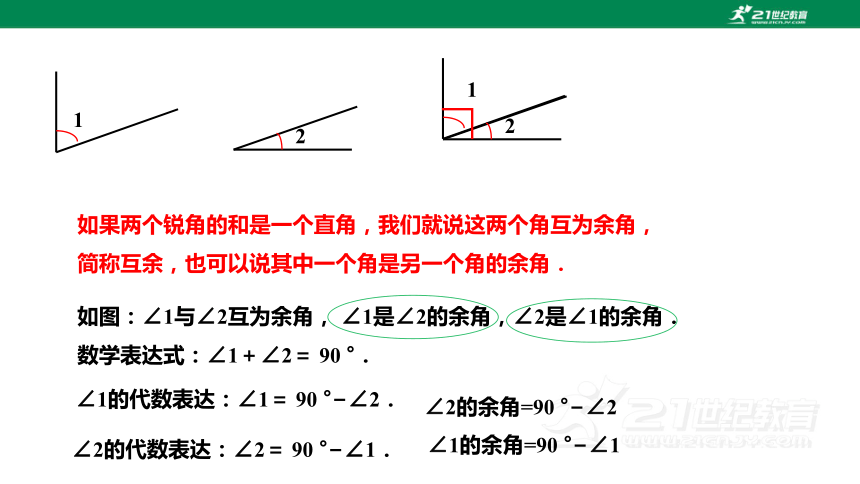
如果两个锐角的和是一个直角，我们就说这两个角互为余角，
简称互余，也可以说其中一个角是另一个角的余角．
如图：∠1与∠2互为余角， ∠1是∠2的余角，∠2是∠1的余角．
数学表达式：∠1＋∠2＝ 90 °．
∠1的代数表达：∠1＝ 90 ° ∠2．
∠2的代数表达：∠2＝ 90 ° ∠1．
∠1的余角=90 ° ∠1
∠2的余角=90 ° ∠2
1
2
1
2
∟
∠AOC+∠BOD=180°－90°=90°
∠AOC与∠BOD互余
如果两个角的和是一个平角，我们就说这两个角互为补角，简称互补，也可以说其中一个角是另一个角的补角．
如图：∠α与∠β互为补角， ∠α是∠β的补角，∠β是∠α的补角．
数学表达式：∠α+∠β=180 °
∠α的代数表达：∠α＝ 180 ° ∠β．
∠β的代数表达：∠β＝ 180 ° ∠α．
∠β的补角＝ 180 ° ∠β．
∠α的补角＝ 180 ° ∠α．
∠AOB的大小可由量角器测得(如图所示)，
则180°－∠AOB的大小为(　　)
A.0° B.70°
C.110° D.180°
B
C
70°
180°－∠AOB=
∠BOC
=∠AOB的 补角
110°
110° 的 补角
∟
∟
∟
等于同一个量的两个量相等
等于同一个量的两个量相等
例2 已知一个角的补角是这个角的余角的4倍，
求这个角的度数.
解:设这个角为x度，
则这个角的余角是（90－x）度，
补角是（180－x）度.
180－x=4（90－x）
x=60
所以这个角的度数为60°.
同角的余角相等.
同角的补角相等.
∵∠1 = 90°-∠3
∠2 = 90°-∠3
∴∠1 =∠2
∟
∟
3
3
几何语言：
等角的余角相等.
等角 的补角相等.
∵∠3=180°-∠1
∠4=180°-∠2
∠1 =∠2
∴∠3 =∠4
几何语言：
∵ ∠3=90°-∠1
∠4=90°-∠2
∠1 =∠2
∴∠3 =∠4
C
D
E
∟
1
2
3
4
1
2
3
4
1.已知∠α与∠β互余，若∠α＝20°，求∠β的度数
　∠β＝90° - ∠α＝90°－20°＝70°.
夯实基础，稳扎稳打
α
β
∟
2.已知∠1与∠2互补，∠1＝38°，求∠2的度数
∠2＝180°－∠1＝180°－38°＝142°.
1
2
3.已知∠α是锐角，则∠α的余角可表示为__________，
∠α的补角可表示为 .
90°-∠α
180°-∠α
它的补角比它的余角大
90
（180-x）-（90-x）
=90
=180-x-90 + x
α
β
α
∟
∟
∟
45°
45°
∠α与∠β互余
∠α=∠β
∠α与∠β互补
∠α=∠β
同角的余角相等.
等角的补角相等.
6.若一个角比它的补角大90°，求这个角的度数
解：设这个角的度数为x度，
则这个角的补角为(180°－x)，
x＝（180°－x）+90°，
x＝135°.
7.若一个角的补角是这个角的余角的3倍，求这个角的度数．
解：设这个角是x度，
则这个角的补角为（180-x）度，余角为（90-x）度，
3（90-x）=180-x，
x=45，
解：设∠2=x，则∠1=x+20，由题意得：∠1+∠2=x+20+x=180， ∴x=80°， ∴∠2=80°，
8.已知∠1与∠2互为补角，且∠1比∠2大20°，
求∠2的度数．
9.一副三角板按如图方式摆放，且∠1的度数比∠2的度数大54°，
求∠2的度数
∠1+∠2=180° - 90°=90°，
∟
∠1=90° - ∠2
90°-∠2＝∠2＋54°，
∠2＝18°.
连续递推，豁然开朗
8.一个角的余角的3倍比它的补角的2倍少120°，求这个角的度数
解　设这个角是x°，根据题意，得
3(90－x)＝2(180－x)－120，
解得x＝30.
即这个角的度数为30°.
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin