第六章 图形的基本知识 章末复习 (2) 课件(共19张PPT)
文档属性
| 名称 | 第六章 图形的基本知识 章末复习 (2) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
第六章 图形的基本知识 章末复习
浙教版七年级上册
分步表达是一种策略
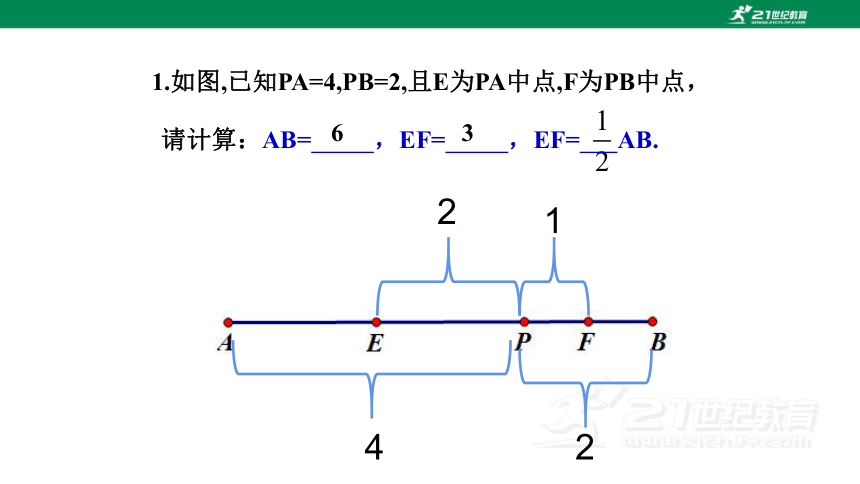
1.如图,已知PA=4,PB=2,且E为PA中点,F为PB中点,
6
3
4
2
请计算:AB= ,EF= ,EF= AB.
2
1
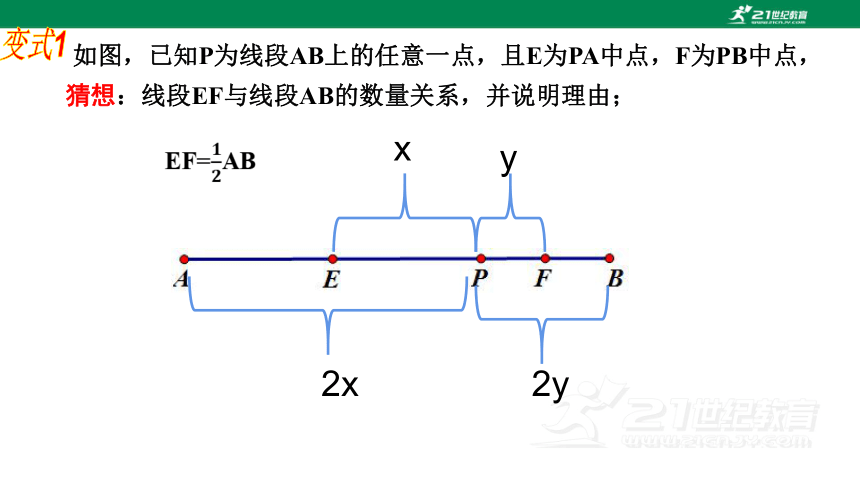
变式1
如图,已知P为线段AB上的任意一点,且E为PA中点,F为PB中点,
猜想:线段EF与线段AB的数量关系,并说明理由;
2x
2y
x
y
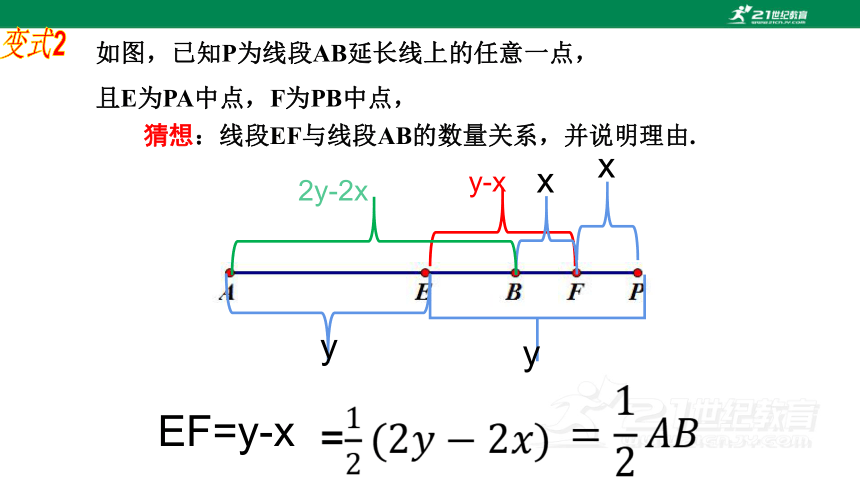
变式2
如图,已知P为线段AB延长线上的任意一点,
且E为PA中点,F为PB中点,
猜想:线段EF与线段AB的数量关系,并说明理由.
y
x
y
y-x
x
EF=y-x
2y-2x
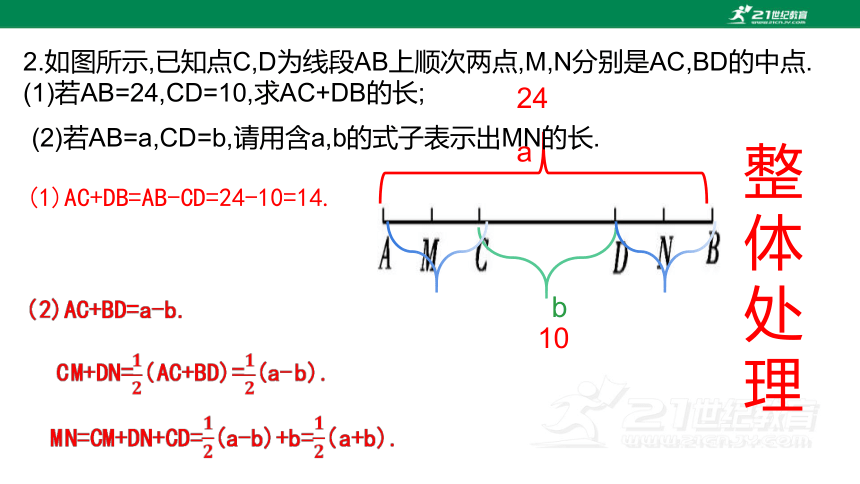
2.如图所示,已知点C,D为线段AB上顺次两点,M,N分别是AC,BD的中点.
(1)若AB=24,CD=10,求AC+DB的长;
(1)AC+DB=AB-CD=24-10=14.
a
b
整体处理
24
10
(2)若AB=a,CD=b,请用含a,b的式子表示出MN的长.
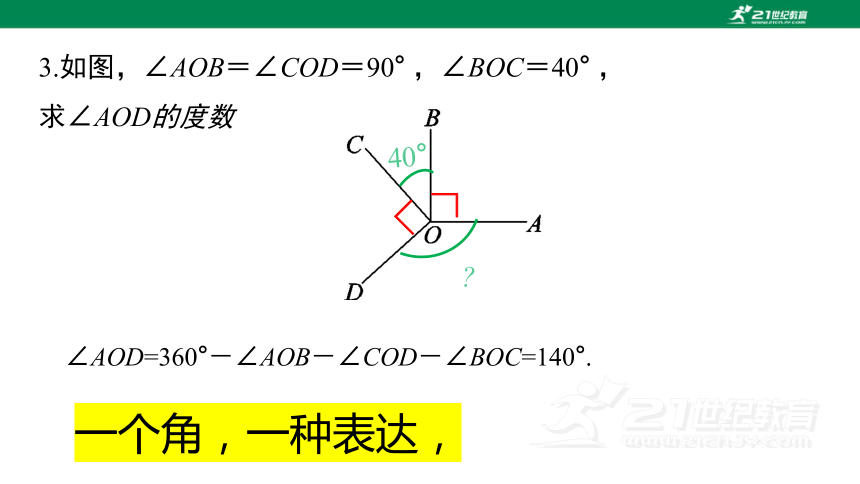
3.如图,∠AOB=∠COD=90° ,∠BOC=40° ,
求∠AOD的度数
∠AOD=360°-∠AOB-∠COD-∠BOC=140°.
∟
∟
40°
一个角,一种表达,
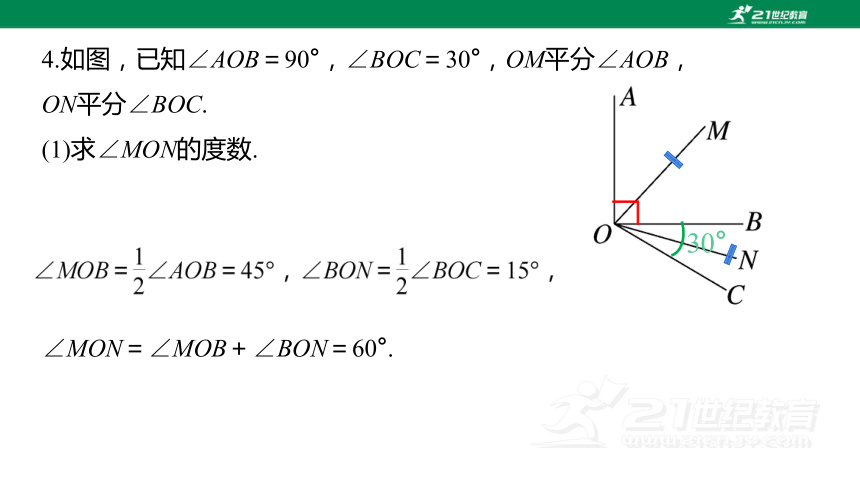
4.如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,
ON平分∠BOC.
(1)求∠MON的度数.
∠MON=∠MOB+∠BON=60°.
∟
30°
(2)如果(1)中∠AOB=α,∠BOC=β(β为锐角),其他条件不变,
求∠MON的度数.
∠MON=∠MOB+∠BON
(3)从(1),(2)的结果中能得出什么结论?
有一个公共顶点、一条公共边,另一边分别在这条公共边的两侧的相邻两个角的角平分线组成的角等于这两个角组成的大角的一半.
α
β
5. 如图,∠AOB是直角,OP平分∠AOB,OQ平分∠AOC,∠POQ=70°,求∠POA、∠AOQ、∠AOC的度数.
∠AOQ=∠POQ-∠POA=70°-45°=25°,
一个角,一种表达,
分步表达是一种策略
∟
70°
一个角,一种表达,
分步表达是一种策略
6.已知点O是直线AB 上一点,∠COD 是直角,OE 平分∠BOC.
(1) 如图,若∠AOC=30°,求∠DOE 的度数
∠BOC=180°-∠AOC=150°.
∠DOE=∠COD-∠COE = 15°.
(2) 在上图中,若∠AOC=α,求∠DOE的度数;
∠BOC=180°-∠AOC=180°-α.
∟
30°
7.如图,OM是∠AOB的平分线,ON是∠BOC的平分线,
∠AOC=50°,求∠BOM,∠BON,∠MON的度数
α
50°
8.如图,已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,求∠AOC、∠MOC、 ∠NOC、∠MON的度数
∠AOC=∠AOB+∠BOC=α+β,
α
β
9.如图,点C 把线段 MN 分成两部分,其长度比 MC :CN=5:4.
若 P是MN的中点,PC=2cm,求 MN的长
MC=5k, CN=4k
MN=MC+CN=5k+4k=9k
PC=PN-CN=4.5k-4k=0.5k
0.5k=2
k=4
一条线段,一种表达,
分步表达是一种策略
10.如图,已知C点分线段AB为5:7两部分,
D点分线段AB为5:11两部分,CD的长为10cm。求AB的长
5k
12k
11. 如图,将一张长方形纸片分别沿着EP,FP折,使点B落在点B',点C落在点C'.若点P,B',C'不在一条直线上,且两条折痕的夹角∠EPF=85°,求∠ B'PC'的度数.
x
x
y
y
x+x+y+y =180
x+y = 85°
-∠ B'PC'
-∠ B'PC'
x+y=∠B'PC'+85°
2(∠B'PC'+85°)-∠B'PC'=180° ,
∠B'PC'=10° .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第六章 图形的基本知识 章末复习
浙教版七年级上册
分步表达是一种策略
1.如图,已知PA=4,PB=2,且E为PA中点,F为PB中点,
6
3
4
2
请计算:AB= ,EF= ,EF= AB.
2
1
变式1
如图,已知P为线段AB上的任意一点,且E为PA中点,F为PB中点,
猜想:线段EF与线段AB的数量关系,并说明理由;
2x
2y
x
y
变式2
如图,已知P为线段AB延长线上的任意一点,
且E为PA中点,F为PB中点,
猜想:线段EF与线段AB的数量关系,并说明理由.
y
x
y
y-x
x
EF=y-x
2y-2x
2.如图所示,已知点C,D为线段AB上顺次两点,M,N分别是AC,BD的中点.
(1)若AB=24,CD=10,求AC+DB的长;
(1)AC+DB=AB-CD=24-10=14.
a
b
整体处理
24
10
(2)若AB=a,CD=b,请用含a,b的式子表示出MN的长.
3.如图,∠AOB=∠COD=90° ,∠BOC=40° ,
求∠AOD的度数
∠AOD=360°-∠AOB-∠COD-∠BOC=140°.
∟
∟
40°
一个角,一种表达,
4.如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,
ON平分∠BOC.
(1)求∠MON的度数.
∠MON=∠MOB+∠BON=60°.
∟
30°
(2)如果(1)中∠AOB=α,∠BOC=β(β为锐角),其他条件不变,
求∠MON的度数.
∠MON=∠MOB+∠BON
(3)从(1),(2)的结果中能得出什么结论?
有一个公共顶点、一条公共边,另一边分别在这条公共边的两侧的相邻两个角的角平分线组成的角等于这两个角组成的大角的一半.
α
β
5. 如图,∠AOB是直角,OP平分∠AOB,OQ平分∠AOC,∠POQ=70°,求∠POA、∠AOQ、∠AOC的度数.
∠AOQ=∠POQ-∠POA=70°-45°=25°,
一个角,一种表达,
分步表达是一种策略
∟
70°
一个角,一种表达,
分步表达是一种策略
6.已知点O是直线AB 上一点,∠COD 是直角,OE 平分∠BOC.
(1) 如图,若∠AOC=30°,求∠DOE 的度数
∠BOC=180°-∠AOC=150°.
∠DOE=∠COD-∠COE = 15°.
(2) 在上图中,若∠AOC=α,求∠DOE的度数;
∠BOC=180°-∠AOC=180°-α.
∟
30°
7.如图,OM是∠AOB的平分线,ON是∠BOC的平分线,
∠AOC=50°,求∠BOM,∠BON,∠MON的度数
α
50°
8.如图,已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,求∠AOC、∠MOC、 ∠NOC、∠MON的度数
∠AOC=∠AOB+∠BOC=α+β,
α
β
9.如图,点C 把线段 MN 分成两部分,其长度比 MC :CN=5:4.
若 P是MN的中点,PC=2cm,求 MN的长
MC=5k, CN=4k
MN=MC+CN=5k+4k=9k
PC=PN-CN=4.5k-4k=0.5k
0.5k=2
k=4
一条线段,一种表达,
分步表达是一种策略
10.如图,已知C点分线段AB为5:7两部分,
D点分线段AB为5:11两部分,CD的长为10cm。求AB的长
5k
12k
11. 如图,将一张长方形纸片分别沿着EP,FP折,使点B落在点B',点C落在点C'.若点P,B',C'不在一条直线上,且两条折痕的夹角∠EPF=85°,求∠ B'PC'的度数.
x
x
y
y
x+x+y+y =180
x+y = 85°
-∠ B'PC'
-∠ B'PC'
x+y=∠B'PC'+85°
2(∠B'PC'+85°)-∠B'PC'=180° ,
∠B'PC'=10° .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
