第5章 一次函数 单元检测能力提升卷(含解析)
文档属性
| 名称 | 第5章 一次函数 单元检测能力提升卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 710.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 10:01:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第5章 一次函数 单元检测能力提升卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C.﹣ D.﹣2
2.下面的点中,在函数y=2x+3的图象上的是( )
A.(﹣2,1) B.(0,2) C.(1,3) D.(﹣1,1)
3.下列关于一次函数y=﹣2x+4的结论中,正确的是( )
A.图象经过点(3,0) B.当x>2时,y<0
C.y随x增大而增大 D.图象经过第二、三、四象限
4.为打造“比、学、赶、帮、超”良好的班风和浓厚的学风,数学白老师为8班孩子购买了5包卡通橡皮和x包表扬信,卡通橡皮每包12元,表扬信每包30元,共花费y元,则关系式为( )
A.y=5x+6 B.y=12x+30 C.y=8x+12 D.y=30x+60
5.如图,在平面直角坐标系中,有函数y=k1x和y=k2x+b的图象,它们相交于点A.下列结论:
①k1<k2 ②b>0 ③当x>2时,则有k1x>k2x+b
④关于x的方程(k1﹣k2)x﹣b=0的解是:x=2
其中正确的有( )
A.①② B.①②③④ C.②③④ D.①③④
6.A,B两地相距12km,甲、乙两人分别从A,B两地沿同一条公路相向而行.他们离A地的距离s(km)与时间t(h)的函数关系如图.则甲出发到相遇的时间为( )
A.1.2h B.1.5h C.1.6h D.1.8h
7.已知点P(﹣1,y1)、点Q(3,y2)在一次函数y=(2m﹣1)x+2的图象上,且y1>y2,则m的取值范围是( )
A. B. C.m≥1 D.m<1
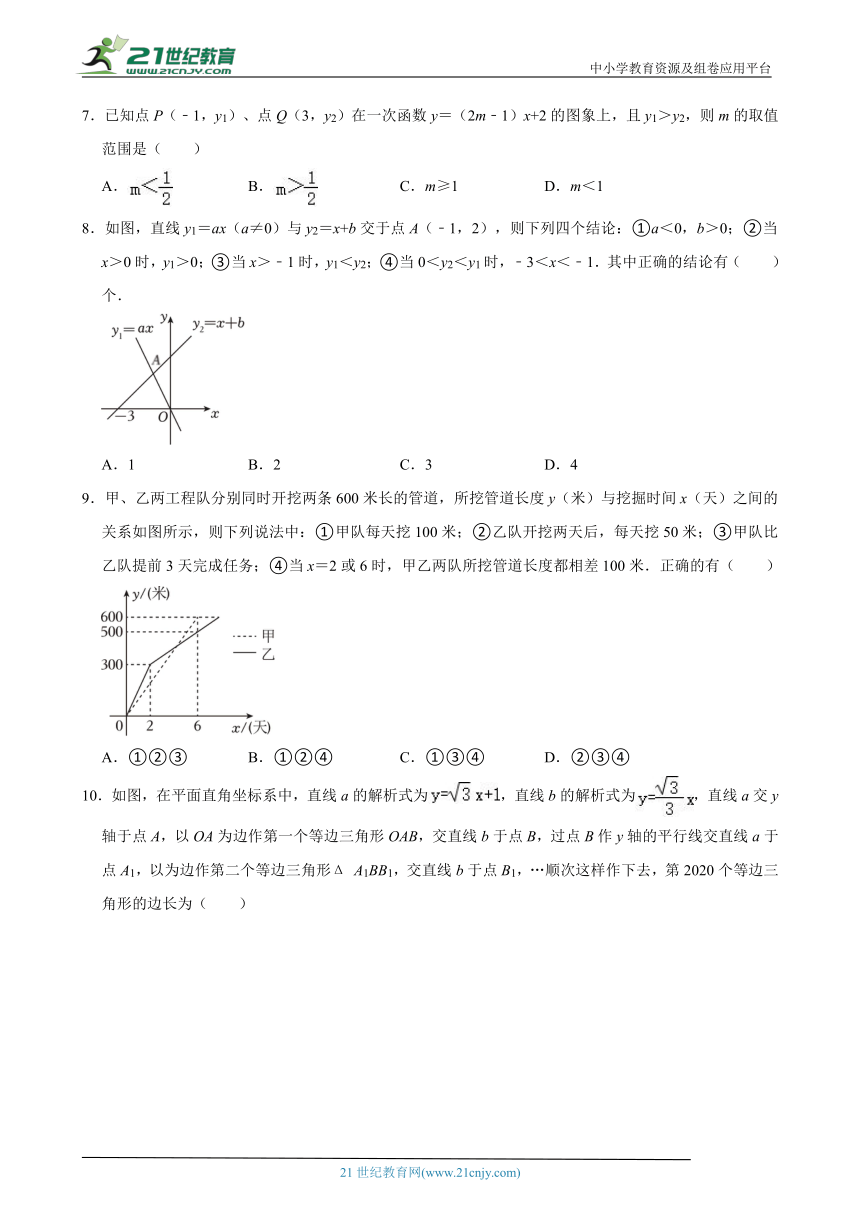
8.如图,直线y1=ax(a≠0)与y2=x+b交于点A(﹣1,2),则下列四个结论:①a<0,b>0;②当x>0时,y1>0;③当x>﹣1时,y1<y2;④当0<y2<y1时,﹣3<x<﹣1.其中正确的结论有( )个.
A.1 B.2 C.3 D.4
9.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲乙两队所挖管道长度都相差100米.正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
10.如图,在平面直角坐标系中,直线a的解析式为,直线b的解析式为,直线a交y轴于点A,以OA为边作第一个等边三角形OAB,交直线b于点B,过点B作y轴的平行线交直线a于点A1,以为边作第二个等边三角形Δ A1BB1,交直线b于点B1,…顺次这样作下去,第2020个等边三角形的边长为( )
A.22019 B.22000 C.4038 D.4040
二、填空题:本题共6小题,每小题3分,共18分。
11.函数中自变量x的取值范围是 .
12.将一次函数y=3x+1的图象沿y轴向下平移3个单位长度后,得到新的一次函数的解析式为 .
13.若直线y=kx+b(k,b是常数,k≠0),过点A(3,2),则关于x的方程kx+2k+b=2的解为 .
14.已知函数y=(k﹣3)x+k.
(1)该函数图象经过定点 .
(2)如果直线y=(k﹣3)x+k不经过第三象限,则k的范围是 .
15.某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kW h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 kW h.
16.已知y1=x+a,y2=﹣2x+4a,对于任意x,m取y1与y2中较小的值,若当2a﹣2≤x≤2a时m有最大值a﹣1,则a= .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.已知y﹣2与x+1成正比例函数关系,且x=﹣2时,y=6.
(1)写出y与x之间的函数关系式;
(2)求当y=4时,x的值.
18.已知一次函数y=kx+b的图象经过点(﹣1,1)和点(1,﹣5).
(1)求一次函数的表达式.
(2)求一次函数的图象与x轴的交点坐标.
19.已知函数y=(2m+1)x+m﹣3.
(1)若函数图象经过原点,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值.
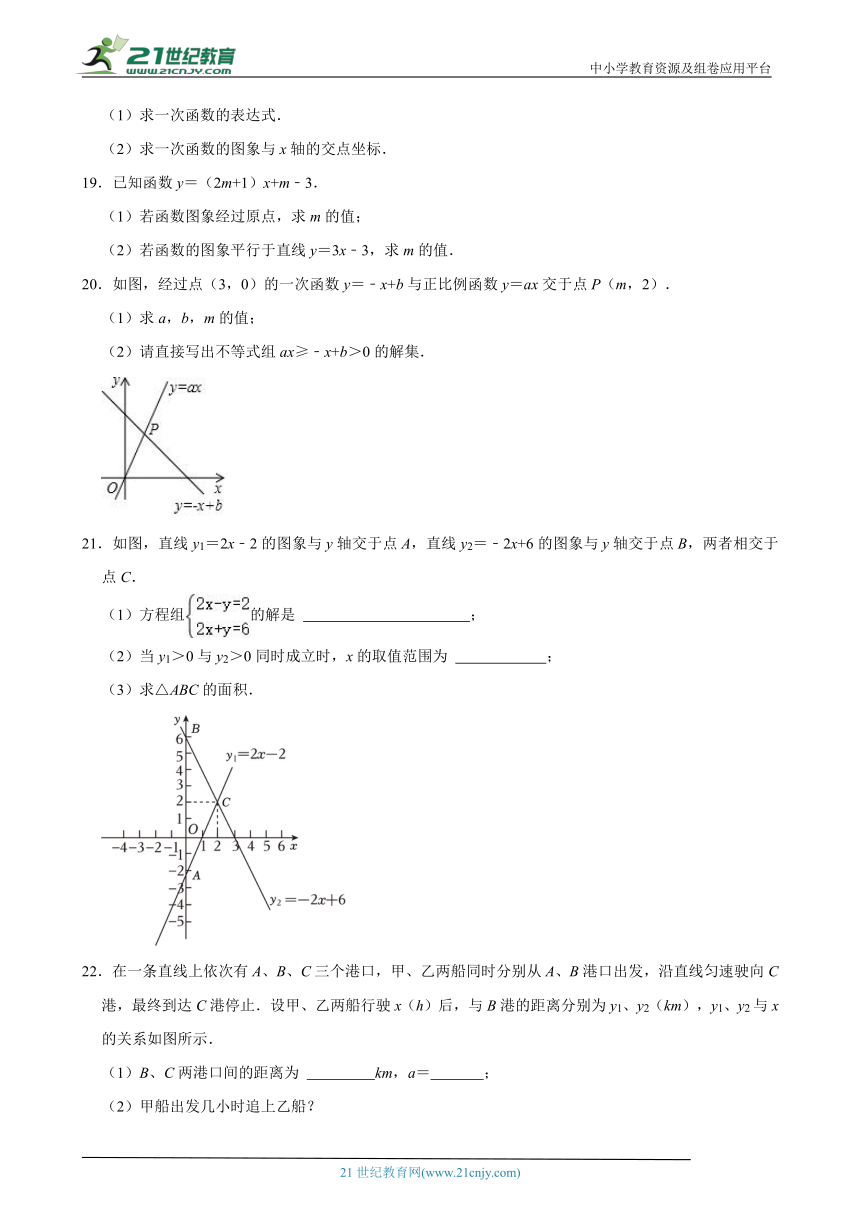
20.如图,经过点(3,0)的一次函数y=﹣x+b与正比例函数y=ax交于点P(m,2).
(1)求a,b,m的值;
(2)请直接写出不等式组ax≥﹣x+b>0的解集.
21.如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 ;
(3)求△ABC的面积.
22.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港停止.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的关系如图所示.
(1)B、C两港口间的距离为 km,a= ;
(2)甲船出发几小时追上乙船?
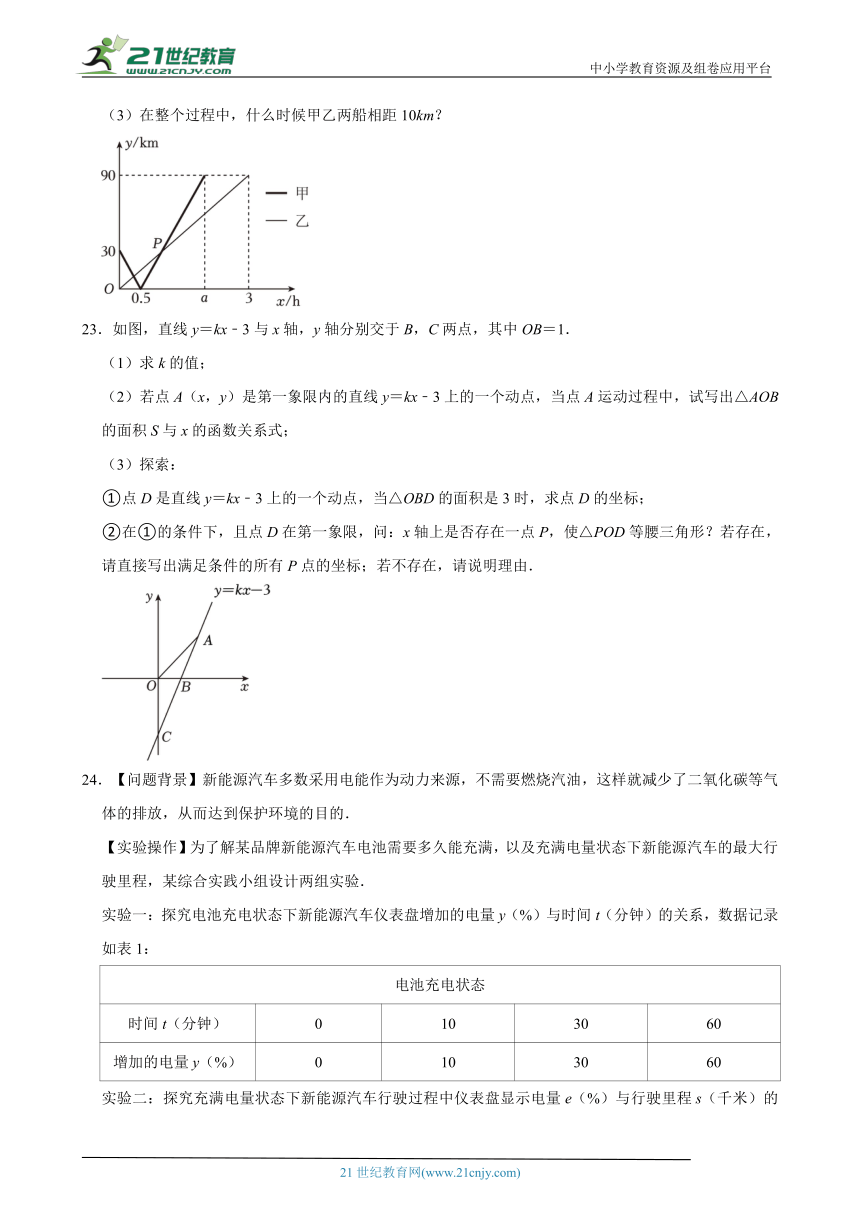
(3)在整个过程中,什么时候甲乙两船相距10km?
23.如图,直线y=kx﹣3与x轴,y轴分别交于B,C两点,其中OB=1.
(1)求k的值;
(2)若点A(x,y)是第一象限内的直线y=kx﹣3上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)探索:
①点D是直线y=kx﹣3上的一个动点,当△OBD的面积是3时,求点D的坐标;
②在①的条件下,且点D在第一象限,问:x轴上是否存在一点P,使△POD等腰三角形?若存在,请直接写出满足条件的所有P点的坐标;若不存在,请说明理由.
24.【问题背景】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的.
【实验操作】为了解某品牌新能源汽车电池需要多久能充满,以及充满电量状态下新能源汽车的最大行驶里程,某综合实践小组设计两组实验.
实验一:探究电池充电状态下新能源汽车仪表盘增加的电量y(%)与时间t(分钟)的关系,数据记录如表1:
电池充电状态
时间t(分钟) 0 10 30 60
增加的电量y(%) 0 10 30 60
实验二:探究充满电量状态下新能源汽车行驶过程中仪表盘显示电量e(%)与行驶里程s(千米)的关系,数据记录如表2:
新能源汽车行驶过程
已行驶里程s(千米) 0 160 200 280
显示电量e(%) 100 60 50 30
【建立模型】(1)观察表1、表2发现都是一次函数模型,请结合表1、表2的数据,求出y关于t的函数解析式及e关于s的函数解析式:
【解决问题】(2)该品牌新能源汽车在充满电量的状态下出发,前往距离出发点500千米处的目的地,若新能源汽车行驶280千米后,在途中的服务区充电30分钟,充电后该新能源汽车是否有足够的电量行驶到目的地.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C.﹣ D.﹣2
【点拨】根据正比例函数的定义可知2a﹣1=0,从而可求得a的值.
【解析】解:∵y=x+2a﹣1是正比例函数,
∴2a﹣1=0.
解得:a=.
故选:A.
【点睛】本题主要考查的是正比例函数的定义,由正比例函数的定义得到2a﹣1=0是解题的关键.
2.下面的点中,在函数y=2x+3的图象上的是( )
A.(﹣2,1) B.(0,2) C.(1,3) D.(﹣1,1)
【点拨】分别将各选项的点坐标代入,然后判断作答即可.
【解析】解:A、当x=﹣2时,y=2×(﹣2)+3=﹣1,则(﹣2,1)不在函数y=2x+3的图象上,不符合题意;
B、当x=0时,y=2×0+3=3,则(0,2)不在函数y=2x+3的图象上,不符合题意;
C、当x=1时,y=2×1+3=5,则(1,3)不在函数y=2x+3的图象上,不符合题意;
D、当x=﹣1时,y=2×(﹣1)+3=1,则(﹣1,1)在函数y=2x+3的图象上,符合题意,
故选:D.
【点睛】本题考查了一次函数图象上点的坐标特征,熟练掌握一次函数图象上点的坐标一定适合此函数的解析式是解题的关键.
3.下列关于一次函数y=﹣2x+4的结论中,正确的是( )
A.图象经过点(3,0) B.当x>2时,y<0
C.y随x增大而增大 D.图象经过第二、三、四象限
【点拨】根据一次函数的性质对各选项进行逐一判断即可.
【解析】解:A、∵当x=3时,y=﹣2,∴图象经过点(3,﹣2),故本选项错误;
B、∵y随x的增大而减小,当x=2时,y=0,∴当x>2时,y<0,故本选项正确.
C、∵k=﹣2<0,∴y随x的增大而减小,故本选项错误;
D、∵k=﹣2<0,b=4>0,∴图象经过第一、二、四象限,故本选项错误;
故选:B.
【点睛】本题考查的是一次函数的性质,熟知一次函数y=kx+b(k≠0),当k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降是解答此题的关键.
4.为打造“比、学、赶、帮、超”良好的班风和浓厚的学风,数学白老师为8班孩子购买了5包卡通橡皮和x包表扬信,卡通橡皮每包12元,表扬信每包30元,共花费y元,则关系式为( )
A.y=5x+6 B.y=12x+30 C.y=8x+12 D.y=30x+60
【点拨】根据题意正确列式即可.
【解析】解:由题意可知,y=30x+5×12=30x+60,
故选:D.
【点睛】本题考查了用关系式表示变量之间的关系,解题的关键是正确运算.
5.如图,在平面直角坐标系中,有函数y=k1x和y=k2x+b的图象,它们相交于点A.下列结论:
①k1<k2 ②b>0 ③当x>2时,则有k1x>k2x+b ④关于x的方程(k1﹣k2)x﹣b=0的解是:x=2
其中正确的有( )
A.①② B.①②③④ C.②③④ D.①③④
【点拨】由正比例函数的性质可判断经过原点的直线为y=k1x,另一条直线为y=k2x+b,由k>0时y随x增大而增大,k<0时y随x增大而减小可判断①;由直线y=k2x+b与y轴交点位置可判断②;由x>2时两条直线的位置可判断③;由两直线交点横坐标为2可得x=2是k1x=k2x+b的解,从而判断④.
【解析】解:∵正比例函数y随x增大而增大,
∴k1>0,
∵直线y=k2x+b中y随x增大而减小,
∴k2<0,
∴k1>k2,①错误.
∵直线y=k2x+b与y轴交点在x轴上方,
∴b>0,②正确.
由图象可得当x>2时直线y=k1x在直线y=k2x+b上方,
∴x>2时,k1x>k2x+b,③正确.
∵两直线交点横坐标为x=2,
∴x=2时,k1x=k2x+b,
∴(k1﹣k2)x﹣b=0的解是x=2,④正确.
故选:C.
【点睛】本题考查一次函数的图象与一元一次方程,一次函数图象与系数的关系,一次函数的性质,解题关键是掌握一次函数与方程及不等式的关系,掌握一次函数图象与系数的关系.
6.A,B两地相距12km,甲、乙两人分别从A,B两地沿同一条公路相向而行.他们离A地的距离s(km)与时间t(h)的函数关系如图.则甲出发到相遇的时间为( )
A.1.2h B.1.5h C.1.6h D.1.8h
【点拨】根据函数图象中的数据,可以分别求得甲乙两人的速度,然后即可求得甲出发到相遇的时间.
【解析】解:由图可得,
甲的速度为:12÷3=4(km/h),
乙的速度为:12÷(3﹣1)=6(km/h),
设甲出发xh,两人相遇,
4x+6(x﹣1)=12,
解得,x=1.8,
故选:D.
【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
7.已知点P(﹣1,y1)、点Q(3,y2)在一次函数y=(2m﹣1)x+2的图象上,且y1>y2,则m的取值范围是( )
A. B. C.m≥1 D.m<1
【点拨】由题目条件可判断出一次函数的增减性,则可得到关于m的不等式,可求得m的取值范围.
【解析】解:
∵点P(﹣1,y1)、点Q(3,y2)在一次函数y=(2m﹣1)x+2的图象上,
∴当﹣1<3时,由题意可知y1>y2,
∴y随x的增大而减小,
∴2m﹣1<0,解得m<,
故选:A.
【点睛】本题主要考查一次函数的性质,得出一次函数的增减性是解题的关键.
8.如图,直线y1=ax(a≠0)与y2=x+b交于点A(﹣1,2),则下列四个结论:①a<0,b>0;②当x>0时,y1>0;③当x>﹣1时,y1<y2;④当0<y2<y1时,﹣3<x<﹣1.其中正确的结论有( )个.
A.1 B.2 C.3 D.4
【点拨】根据正比例函数和一次函数的性质,结合图象判断即可,关键是根据正比例函数和一次函数的性质判断.
【解析】解:因为y1=ax(a≠0)经过二,四象限,所以a<0,y2=x+b经过一、二、三象限,所以b>0,故①正确;
∵a<0,当x>0时,y1<0,故②错误;
结合图象可得,当x>﹣1时,直线y1=ax(a≠0)的图象在y2=x+b的图象下方,y1<y2,故③正确;
结合图象,当y2<y1时,x<﹣1,∵0<y2<y1,∴x>﹣3,∴﹣3<x<﹣1,故④正确.
故选:C.
【点睛】本题考查一次函数与一元一次不等式,正确记忆相关知识点是解题关键.
9.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲乙两队所挖管道长度都相差100米.正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
【点拨】①根据函数图象由工作效率=工作总量÷工作时间就可以得出结论;
②根据函数图象由工作效率=工作总量÷工作时间就可以得出结论;
③根据函数图象求出乙队完成的时间就可以求出结论;
④由甲的工作效率就可以求出2天时的工作量为200米,乙队是300米.6天时甲队是600米,乙队是500米得出300﹣200=600﹣500=100米故得出结论.
【解析】解:①根据函数图象得:
甲队的工作效率为:600÷6=100米/天,故①正确;
②根据函数图象,得:
乙队开挖两天后的工作效率为:(500﹣300)÷(6﹣2)=50米/天,故②正确;
③乙队完成任务的时间为:2+(600﹣300)÷50=8(天),
∴甲队提前的时间为:8﹣6=2(天).
∵2≠3,
∴③错误;
④当x=2时,甲队完成的工作量为:2×100=200米,
乙队完成的工作量为:300米.
当x=6时,甲队完成的工作量为600米,乙队完成的工作量为500米.
∵300﹣200=600﹣500=100,
∴当x=2或6时,甲乙两队所挖管道长度都相差100米,
故④正确.
∴正确的有①②④.
故选:B.
【点睛】本题考查了一次函数的图象的性质的运用,工程问题的数量关系:工作总量=工作效率×工作时间的运用,解答时分析清楚一次函数的图象的意义是关键.
10.如图,在平面直角坐标系中,直线a的解析式为,直线b的解析式为,直线a交y轴于点A,以OA为边作第一个等边三角形OAB,交直线b于点B,过点B作y轴的平行线交直线a于点A1,以为边作第二个等边三角形Δ A1BB1,交直线b于点B1,…顺次这样作下去,第2020个等边三角形的边长为( )
A.22019 B.22000 C.4038 D.4040
【点拨】延长A1B交x轴于D,A2B1交x轴于E,根据等边三角形的性质得OA=OB,A1B=BB1,A2B1=B2B1,直线b的解析式为,得∠BOD=30°,由直线a的解析式得第一个等边三角形边长为1,解Rt△OBD得,BD=1/2,把代入求得A1的纵坐标,即可求得第二个等边三角形的边长,从而找出规律,按照此规律即可求得第2020个等边三角形的边长.
【解析】解:延长A1B交x轴于D,延长A2B1交x轴于E,
∵△OAB,△BA1B1,△B1A2B2均为等边三角形,
∴OA=OB,A1B=BB1,A2B1=B2B1,
∵直线b的解析式为:,
∴∠BOD=30°,
对于直线a,,当x=0时,y=1,
∴点A的坐标为(0,1),
∴OA=OB=1,
在Rt△OBD中,OB=1,∠BOD=30°,
∴,,
∴点B的坐标为,
对于,当时,,
∴点A1的坐标为,
∴,
∴A1B=BB1=AD﹣BD=2=21,
∴OB1=OB+BB1=3,
在Rt△AB1E中,OB1=3,∠B1OE=30°,
∴,,
∴点B1的坐标为,
对于,当时,,
∴,
∴A2B1=A2E=B1E=4=22,
同理得:A3B2=23,……,
以此类推,第n个等边三角形的边长为2n﹣1,
∴第2020个等边三角形的边长为22019.
故选:A.
【点睛】本题考查了一次函数图象上点的坐标特征、等边三角形的性质,根据等边三角形的性质找出第n个等边三角形的边长为2n﹣1是解题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.函数中自变量x的取值范围是 x≥﹣2且x≠2 .
【点拨】根据二次根式的性质和分式的意义,即可求解.
【解析】解:∵分母不能为0,二次根式的被开方数为非负数,
∴x+2≥0,且2x﹣4≠0,
解得:x≥﹣2且x≠2,
故答案为:x≥﹣2且x≠2.
【点睛】本题考查了函数自变量的取值范围,解题的关键是:熟练掌握二次根式的性质和分式的意义.
12.将一次函数y=3x+1的图象沿y轴向下平移3个单位长度后,得到新的一次函数的解析式为 y=3x﹣2 .
【点拨】根据函数图象的平移规律,上加下减,可得答案.
【解析】解:由一次函数y=3x+1的图象沿y轴向下平移3个单位后,得到的图象对应的函数关系式为y=3x+1﹣3,
化简,得y=3x﹣2,
故答案为:y=3x﹣2.
【点睛】此题主要考查了一次函数图象与几何变换,求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.解析式变化的规律是:左加右减,上加下减.
13.若直线y=kx+b(k,b是常数,k≠0),过点A(3,2),则关于x的方程kx+2k+b=2的解为 x=1 .
【点拨】根据直线y=kx+b过点A(3,2),得出2=3k+b,把2=3k+b代入方程kx+2k+b=2,整理得出k(x﹣1)=0,根据k≠0,得出x﹣1=0,求出x的值即可.
【解析】解:∵直线y=kx+b过点A(3,2),
∴2=3k+b,
把2=3k+b代入kx+2k+b=2得:kx+2k+b=3k+b,
整理得:k(x﹣1)=0,
∵k≠0,
∴x﹣1=0,
解得:x=1.
故答案为:x=1.
【点睛】本题主要考查了一次函数与一元一次方程,一次函数的性质,解答本题的关键是熟练掌握一次函数的性质.
14.已知函数y=(k﹣3)x+k.
(1)该函数图象经过定点 (﹣1,3) .
(2)如果直线y=(k﹣3)x+k不经过第三象限,则k的范围是 0≤k≤3 .
【点拨】(1)根据“y=(k﹣3)x+k=k(x+1)﹣3x”来求解;
(2)由一次函数不经过第三象限可得到关于k的不等式组,则可求得k的取值范围.
【解析】解:(1)∵y=(k﹣3)x+k=k(x+1)﹣3x,
∴该函数过定点(﹣1,3).
故答案为:(﹣1,3).
(2)∵直线y=(k﹣3)x+k不经过第三象限,
∴,
解得0≤k≤3,
故答案为:0≤k≤3.
【点睛】本题考查了一次函数图象上点的坐标特征,一次函数图象与系数的关系,解答此题的关键是熟知一次函数图象上点的坐标特点,确定函数与系数之间的关系,进而求解.
15.某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kW h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 12 kW h.
【点拨】根据“电动汽车每千米的耗电量=剩余电量的减少量÷行驶路程”分别计算A、B两款新能源电动汽车每千米的耗电量,由此写出图象l1,l2的函数关系式,将x=300分别代入,求出对应函数值并计算二者之差即可.
【解析】解:A款新能源电动汽车每千米的耗电量为(80﹣48)÷200=0.16(kW h),B款新能源电动汽车每千米的耗电量为(80﹣40)÷200=0.2(kW h),
∴l1图象的函数关系式为y1=80﹣0.16x,l2图象的函数关系式为y2=80﹣0.2x,
当x=300时,y1=80﹣0.16×300=32,y2=80﹣0.2×300=20,
32﹣20=12(kW h),
∴当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多12kW h.
故答案为:12.
【点睛】本题考查一次函数的应用,根据“电动汽车每千米的耗电量=剩余电量的减少量÷行驶路程”分别计算A、B两款新能源电动汽车每千米的耗电量,由此写出图象l1,l2的函数关系式,并计算当x=300时对应函数值是解题的关键.
16.已知y1=x+a,y2=﹣2x+4a,对于任意x,m取y1与y2中较小的值,若当2a﹣2≤x≤2a时m有最大值a﹣1,则a= ﹣0.5或5 .
【点拨】分两种情况讨论,当y1>y2,则x+a>﹣2x+4a,即x>a时,当y1<y2,则x+a<﹣2x+4a,即x<a时,分别求出a的值即可.
【解析】解:当y1>y2,则x+a>﹣2x+4a,
解得:x>a,
即x>a时,m=﹣2x+4a,
∵﹣2<0,
∴m随x的增大而减小,
∴当x=2a﹣2时,m取最大值,即﹣2(2a﹣2)+4a=a﹣1,
解得:a=5,
当a=5时,2a﹣2>a,符合题意;
当y1<y2,则x+a<﹣2x+4a,
解得:x<a,
即x<a时,m=x+a,
∵1>0,
∴m随x的增大而增大,
∴当x=2a时,m取最大值,即2a+a=a﹣1,
解得:a=﹣0.5,
当a=﹣0.5时,2a<a,符合题意;
综上分析可知,a=5或﹣0.5.
故答案为:﹣0.5或5.
【点睛】本题主要考查了一次函数的性质,一元一次方程的应用,解题的关键是理解题意,能进行分类讨论解题.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.已知y﹣2与x+1成正比例函数关系,且x=﹣2时,y=6.
(1)写出y与x之间的函数关系式;
(2)求当y=4时,x的值.
【点拨】(1)根据正比例函数的定义设y﹣2=k(x+1),然后把已知的对应值代入求出k,从而得到y与x的关系式;
(2)利用(1)中的解析式得到﹣4x﹣2=4,然后解方程即可.
【解析】解:(1)根据题意,设y﹣2=k(x+1),
把x=﹣2,y=6代入得6﹣2=k×(﹣2+1),
解得k=﹣4,
∴y﹣2=﹣4(x+1),
∴y与x之间的函数关系式为y=﹣4x﹣2;
(2)当y=4时,﹣4x﹣2=4,
解得x=﹣.
【点睛】本题考查了待定系数法求一次函数解析式:求一次函数y=kx+b,则需要两组x,y的值.
18.已知一次函数y=kx+b的图象经过点(﹣1,1)和点(1,﹣5).
(1)求一次函数的表达式.
(2)求一次函数的图象与x轴的交点坐标.
【点拨】(1)把(﹣1,1)和(1,﹣5)代入y=kx+b求出k,b的值即可得出函数解析式;
(2)令y=0,求出x的值即可.
【解析】解:(1)把(﹣1,1)和(1,﹣5)代入y=kx+b得,
,
解得,
∴一次函数的表达式为y=﹣3x﹣2;
(2)当y=0时,由﹣3x﹣2=0,
解得,
∴一次函数的图象与x轴的交点坐标为.
【点睛】本题考查的是利用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,熟知利用待定系数法求一次函数解析式一般步骤是解题的关键.
19.已知函数y=(2m+1)x+m﹣3.
(1)若函数图象经过原点,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值.
【点拨】(1)根据一次函数图象上点的坐标特征,把原点坐标代入y=(2m+1)x+m﹣3可计算出m的值;
(2)根据两直线平行的问题得到2m+1=3,然后解一次方程即可.
【解析】解:(1)∵y=(2m+1)x+m﹣3经过原点,是正比例函数,
∴.
解得:m=3.
(2)∵函数的图象平行于直线y=3x﹣3,
∴2m+1=3,
解得:m=1.
【点睛】本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了一次函数图象上点的坐标特征.
20.如图,经过点(3,0)的一次函数y=﹣x+b与正比例函数y=ax交于点P(m,2).
(1)求a,b,m的值;
(2)请直接写出不等式组ax≥﹣x+b>0的解集.
【点拨】(1)将点(3,0)和点P的坐标代入一次函数的解析式求得m、b的值,然后将点P的坐标代入正比例函数即可求得a的值;
(2)直接根据函数的图象结合点P的坐标确定不等式的解集即可.
【解析】解:(1)∵经过点(3,0)的一次函数y=﹣x+b与正比例函数y=ax交于点P(m,2).
∴﹣3+b=0,
∴b=3,
∴y=﹣x+3,
∴2=﹣m+3,
∴m=1,
∴P(1,2),
∴a=2.
(2)观察图象得:不等式组ax≥﹣x+b>0的解集为1≤x<3.
【点睛】考查了一次函数与一元一次不等式的问题,解题的关键是能够确定有关待定系数的值,难度不大.
21.如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 1<x<3 ;
(3)求△ABC的面积.
【点拨】(1)根据题意画出图象,利用其交点坐标得出方程组的解;
(2)利用函数图象得出在x轴上方时,对应x的取值范围;
(3)利用已知图象结合三角形面积求法得出答案.
【解析】解:(1)如图所示:方程组组的解为:;
故答案为:;
(2)如图所示:当y1>0与y2>0同时成立时,
x取何值范围是:1<x<3;
故答案为:1<x<3;
(3)∵令x=0,则y1=﹣2,y2=6,
∴A(0,﹣2),B(0,6).
∴AB=8.
∴S△ABC=×8×2=8.
【点睛】此题主要考查了一次函数与二元一次方程组以及一次函数与一元一次不等式和三角形面积求法等知识,正确利用数形结合分析是解题关键.
22.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港停止.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的关系如图所示.
(1)B、C两港口间的距离为 90 km,a= 2 ;
(2)甲船出发几小时追上乙船?
(3)在整个过程中,什么时候甲乙两船相距10km?
【点拨】(1)由甲船行驶的函数图象可以看出,甲船从A港出发,0.5h后到达B港,a h后到达C港,又由于甲船行驶速度不变,则可以求出a的值;
(2)分别求出0.5h后甲乙两船行驶的函数表达式,联立即可求解;
(3)分三种情形分别求解即可解决问题;
【解析】解:(1)B、C两港口间距离s=90(km),
又由于甲船行驶速度不变,
故30÷0.5=60(km/h),
则a=2(h).
故答案为:90,2;
(2)由点(3,90)求得,y2=30x.
当0.5<x≤2时,设解析式为y1=ax+c,
由点(0.5,0),(2,90)在图象上,
∴,
解得:,
∴y1=60x﹣30,
当y1=y2时,60x﹣30=30x,解得,x=1.
此时y1=y2=30.
所以点P的坐标为(1,30);
(3)当甲船还未追上乙船时,30x﹣(60x﹣30)=10.
解:x=
②当Ψ船追上乙船后,当未到达C港口时:(60x﹣30)﹣30x=10.解得:x=,
③当甲船到达C港口,乙船还未到达C港口时:90﹣30x=10.
解得:x=
综上:当经过或或时,甲乙两船相距10km.
【点睛】此题主要考查了一次函数的应用以及函数方程、函数图象与实际结合的问题,利用数形结合得出关键点坐标是解题关键.
23.如图,直线y=kx﹣3与x轴,y轴分别交于B,C两点,其中OB=1.
(1)求k的值;
(2)若点A(x,y)是第一象限内的直线y=kx﹣3上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)探索:
①点D是直线y=kx﹣3上的一个动点,当△OBD的面积是3时,求点D的坐标;
②在①的条件下,且点D在第一象限,问:x轴上是否存在一点P,使△POD等腰三角形?若存在,请直接写出满足条件的所有P点的坐标;若不存在,请说明理由.
【点拨】(1)由OB=1可得出点B坐标,将点B的坐标代入直线解析式中即可得出k;
(2)直接利用三角形的面积公式即可得出结论;
(3)①当△OBD的面积是3时,则△OBD的高为6,即点D到x轴距离为6,据此求解即可;
②设出点P的坐标,进而利用两点间的距离公式求出OD2,OP2,DP2,分三种情况用两边相等建立方程求解即可.
【解析】解:(1),直线y=kx﹣3与x轴,y轴分别交于B,C两点,其中OB=1,
∴B(1,0),
交点B的坐标代入y=kx﹣3中,得:
k﹣3=0,
解得k=3,
∴y=3x﹣3,
∴k的值为3;
(2)∵点A(x,y)是第一象限内的直线y=3x﹣3上的一个动点,
∴△AOB的面积;
(3)①∵△OBD的面积是3,OB=1,
∴△OBD的高为6,
∴点D到x轴距离为6,
∵点D是直线y=3x﹣3上的一个动点,
∴y=3x﹣3=6时,x=3,
y=3x﹣3=﹣6时,x=﹣1,
∴点D的坐标为(3,6)或(﹣1,﹣6);
②x轴上存在一点P,使△POD等腰三角形;理由如下:
∵在①的条件下,且点D在第一象限,
∴点D的坐标为(3,6),
设点P(m,0),
∴OD2=32+62=45,OP2=m2,DP2=(m﹣3)2+36,
∵△DOP为等腰三角形,
∴当OD=OP时,OD2=OP2,即:45=m2,
解得,
此时点P坐标为,;
当OD=DP时,OD2=DP2,即:45=(m﹣3)2+36,
解得m=0(此时和点A重合,舍去)或m=6,
此时点P坐标为(6,0);
当OP=DP时,OP2=DP2,即:m2=(m﹣3)2+36,
解得,
此时点P坐标为;
即:满足条件的P点坐标为,,(6,0),.
【点睛】此题是一次函数综合题,主要考查了一次函数的图象与性质,待定系数法,三角形的面积公式,等腰三角形的性质,解答本题的关键是熟练掌握一次函数的性质.
24.【问题背景】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的.
【实验操作】为了解某品牌新能源汽车电池需要多久能充满,以及充满电量状态下新能源汽车的最大行驶里程,某综合实践小组设计两组实验.
实验一:探究电池充电状态下新能源汽车仪表盘增加的电量y(%)与时间t(分钟)的关系,数据记录如表1:
电池充电状态
时间t(分钟) 0 10 30 60
增加的电量y(%) 0 10 30 60
实验二:探究充满电量状态下新能源汽车行驶过程中仪表盘显示电量e(%)与行驶里程s(千米)的关系,数据记录如表2:
新能源汽车行驶过程
已行驶里程s(千米) 0 160 200 280
显示电量e(%) 100 60 50 30
【建立模型】(1)观察表1、表2发现都是一次函数模型,请结合表1、表2的数据,求出y关于t的函数解析式及e关于s的函数解析式:
【解决问题】(2)该品牌新能源汽车在充满电量的状态下出发,前往距离出发点500千米处的目的地,若新能源汽车行驶280千米后,在途中的服务区充电30分钟,充电后该新能源汽车是否有足够的电量行驶到目的地.
【点拨】(1)根据表1中数据变化规律直接写出y关于t的函数解析式,利用待定系数法求出e关于s的函数解析式即可;
(2)将s=280代入e关于s的函数解析式,求出剩余电量;将t=30代入y关于t的函数解析式,求出充入的电量,从而求出在途中的服务区充电30分钟后仪表盘显示的电量,将它代入e关于s的函数解析式,求出能够行驶的距离并与剩余的路程相比即可得出结论.
【解析】解:(1)由表格中的数据可知,y关于t的函数解析式为:y=t;
设e关于s的函数解析式为e=k2s+b(k2、b为常数,且k2≠0),
将s=0,e=100和s=160,e=6(0分)别代入e=k2s+b,
得,
解得,
∴e关于s的函数解析式为:e=﹣s+100;
(2)当s=280时,e=﹣×280+100=30,
当t=30时,y=30,
30+30=60,
∴在途中的服务区充电30分钟后,仪表盘显示电量是60%.
当e=60时,60=﹣s+100,解得s=160,
∴当仪表盘显示电量为60%时还能行驶160千米.
剩余路程为500﹣280=220(千米),
∵160<220,
∴充电后该新能源汽车没有足够的电量行驶到目的地.
【点睛】本题考查了函数关系式,函数值,掌握待定系数法求函数的解析式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第5章 一次函数 单元检测能力提升卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C.﹣ D.﹣2
2.下面的点中,在函数y=2x+3的图象上的是( )
A.(﹣2,1) B.(0,2) C.(1,3) D.(﹣1,1)
3.下列关于一次函数y=﹣2x+4的结论中,正确的是( )
A.图象经过点(3,0) B.当x>2时,y<0
C.y随x增大而增大 D.图象经过第二、三、四象限
4.为打造“比、学、赶、帮、超”良好的班风和浓厚的学风,数学白老师为8班孩子购买了5包卡通橡皮和x包表扬信,卡通橡皮每包12元,表扬信每包30元,共花费y元,则关系式为( )
A.y=5x+6 B.y=12x+30 C.y=8x+12 D.y=30x+60
5.如图,在平面直角坐标系中,有函数y=k1x和y=k2x+b的图象,它们相交于点A.下列结论:
①k1<k2 ②b>0 ③当x>2时,则有k1x>k2x+b
④关于x的方程(k1﹣k2)x﹣b=0的解是:x=2
其中正确的有( )
A.①② B.①②③④ C.②③④ D.①③④
6.A,B两地相距12km,甲、乙两人分别从A,B两地沿同一条公路相向而行.他们离A地的距离s(km)与时间t(h)的函数关系如图.则甲出发到相遇的时间为( )
A.1.2h B.1.5h C.1.6h D.1.8h
7.已知点P(﹣1,y1)、点Q(3,y2)在一次函数y=(2m﹣1)x+2的图象上,且y1>y2,则m的取值范围是( )
A. B. C.m≥1 D.m<1
8.如图,直线y1=ax(a≠0)与y2=x+b交于点A(﹣1,2),则下列四个结论:①a<0,b>0;②当x>0时,y1>0;③当x>﹣1时,y1<y2;④当0<y2<y1时,﹣3<x<﹣1.其中正确的结论有( )个.
A.1 B.2 C.3 D.4
9.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲乙两队所挖管道长度都相差100米.正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
10.如图,在平面直角坐标系中,直线a的解析式为,直线b的解析式为,直线a交y轴于点A,以OA为边作第一个等边三角形OAB,交直线b于点B,过点B作y轴的平行线交直线a于点A1,以为边作第二个等边三角形Δ A1BB1,交直线b于点B1,…顺次这样作下去,第2020个等边三角形的边长为( )
A.22019 B.22000 C.4038 D.4040
二、填空题:本题共6小题,每小题3分,共18分。
11.函数中自变量x的取值范围是 .
12.将一次函数y=3x+1的图象沿y轴向下平移3个单位长度后,得到新的一次函数的解析式为 .
13.若直线y=kx+b(k,b是常数,k≠0),过点A(3,2),则关于x的方程kx+2k+b=2的解为 .
14.已知函数y=(k﹣3)x+k.
(1)该函数图象经过定点 .
(2)如果直线y=(k﹣3)x+k不经过第三象限,则k的范围是 .
15.某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kW h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 kW h.
16.已知y1=x+a,y2=﹣2x+4a,对于任意x,m取y1与y2中较小的值,若当2a﹣2≤x≤2a时m有最大值a﹣1,则a= .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.已知y﹣2与x+1成正比例函数关系,且x=﹣2时,y=6.
(1)写出y与x之间的函数关系式;
(2)求当y=4时,x的值.
18.已知一次函数y=kx+b的图象经过点(﹣1,1)和点(1,﹣5).
(1)求一次函数的表达式.
(2)求一次函数的图象与x轴的交点坐标.
19.已知函数y=(2m+1)x+m﹣3.
(1)若函数图象经过原点,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值.
20.如图,经过点(3,0)的一次函数y=﹣x+b与正比例函数y=ax交于点P(m,2).
(1)求a,b,m的值;
(2)请直接写出不等式组ax≥﹣x+b>0的解集.
21.如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 ;
(3)求△ABC的面积.
22.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港停止.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的关系如图所示.
(1)B、C两港口间的距离为 km,a= ;
(2)甲船出发几小时追上乙船?
(3)在整个过程中,什么时候甲乙两船相距10km?
23.如图,直线y=kx﹣3与x轴,y轴分别交于B,C两点,其中OB=1.
(1)求k的值;
(2)若点A(x,y)是第一象限内的直线y=kx﹣3上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)探索:
①点D是直线y=kx﹣3上的一个动点,当△OBD的面积是3时,求点D的坐标;
②在①的条件下,且点D在第一象限,问:x轴上是否存在一点P,使△POD等腰三角形?若存在,请直接写出满足条件的所有P点的坐标;若不存在,请说明理由.
24.【问题背景】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的.
【实验操作】为了解某品牌新能源汽车电池需要多久能充满,以及充满电量状态下新能源汽车的最大行驶里程,某综合实践小组设计两组实验.
实验一:探究电池充电状态下新能源汽车仪表盘增加的电量y(%)与时间t(分钟)的关系,数据记录如表1:
电池充电状态
时间t(分钟) 0 10 30 60
增加的电量y(%) 0 10 30 60
实验二:探究充满电量状态下新能源汽车行驶过程中仪表盘显示电量e(%)与行驶里程s(千米)的关系,数据记录如表2:
新能源汽车行驶过程
已行驶里程s(千米) 0 160 200 280
显示电量e(%) 100 60 50 30
【建立模型】(1)观察表1、表2发现都是一次函数模型,请结合表1、表2的数据,求出y关于t的函数解析式及e关于s的函数解析式:
【解决问题】(2)该品牌新能源汽车在充满电量的状态下出发,前往距离出发点500千米处的目的地,若新能源汽车行驶280千米后,在途中的服务区充电30分钟,充电后该新能源汽车是否有足够的电量行驶到目的地.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C.﹣ D.﹣2
【点拨】根据正比例函数的定义可知2a﹣1=0,从而可求得a的值.
【解析】解:∵y=x+2a﹣1是正比例函数,
∴2a﹣1=0.
解得:a=.
故选:A.
【点睛】本题主要考查的是正比例函数的定义,由正比例函数的定义得到2a﹣1=0是解题的关键.
2.下面的点中,在函数y=2x+3的图象上的是( )
A.(﹣2,1) B.(0,2) C.(1,3) D.(﹣1,1)
【点拨】分别将各选项的点坐标代入,然后判断作答即可.
【解析】解:A、当x=﹣2时,y=2×(﹣2)+3=﹣1,则(﹣2,1)不在函数y=2x+3的图象上,不符合题意;
B、当x=0时,y=2×0+3=3,则(0,2)不在函数y=2x+3的图象上,不符合题意;
C、当x=1时,y=2×1+3=5,则(1,3)不在函数y=2x+3的图象上,不符合题意;
D、当x=﹣1时,y=2×(﹣1)+3=1,则(﹣1,1)在函数y=2x+3的图象上,符合题意,
故选:D.
【点睛】本题考查了一次函数图象上点的坐标特征,熟练掌握一次函数图象上点的坐标一定适合此函数的解析式是解题的关键.
3.下列关于一次函数y=﹣2x+4的结论中,正确的是( )
A.图象经过点(3,0) B.当x>2时,y<0
C.y随x增大而增大 D.图象经过第二、三、四象限
【点拨】根据一次函数的性质对各选项进行逐一判断即可.
【解析】解:A、∵当x=3时,y=﹣2,∴图象经过点(3,﹣2),故本选项错误;
B、∵y随x的增大而减小,当x=2时,y=0,∴当x>2时,y<0,故本选项正确.
C、∵k=﹣2<0,∴y随x的增大而减小,故本选项错误;
D、∵k=﹣2<0,b=4>0,∴图象经过第一、二、四象限,故本选项错误;
故选:B.
【点睛】本题考查的是一次函数的性质,熟知一次函数y=kx+b(k≠0),当k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降是解答此题的关键.
4.为打造“比、学、赶、帮、超”良好的班风和浓厚的学风,数学白老师为8班孩子购买了5包卡通橡皮和x包表扬信,卡通橡皮每包12元,表扬信每包30元,共花费y元,则关系式为( )
A.y=5x+6 B.y=12x+30 C.y=8x+12 D.y=30x+60
【点拨】根据题意正确列式即可.
【解析】解:由题意可知,y=30x+5×12=30x+60,
故选:D.
【点睛】本题考查了用关系式表示变量之间的关系,解题的关键是正确运算.
5.如图,在平面直角坐标系中,有函数y=k1x和y=k2x+b的图象,它们相交于点A.下列结论:
①k1<k2 ②b>0 ③当x>2时,则有k1x>k2x+b ④关于x的方程(k1﹣k2)x﹣b=0的解是:x=2
其中正确的有( )
A.①② B.①②③④ C.②③④ D.①③④
【点拨】由正比例函数的性质可判断经过原点的直线为y=k1x,另一条直线为y=k2x+b,由k>0时y随x增大而增大,k<0时y随x增大而减小可判断①;由直线y=k2x+b与y轴交点位置可判断②;由x>2时两条直线的位置可判断③;由两直线交点横坐标为2可得x=2是k1x=k2x+b的解,从而判断④.
【解析】解:∵正比例函数y随x增大而增大,
∴k1>0,
∵直线y=k2x+b中y随x增大而减小,
∴k2<0,
∴k1>k2,①错误.
∵直线y=k2x+b与y轴交点在x轴上方,
∴b>0,②正确.
由图象可得当x>2时直线y=k1x在直线y=k2x+b上方,
∴x>2时,k1x>k2x+b,③正确.
∵两直线交点横坐标为x=2,
∴x=2时,k1x=k2x+b,
∴(k1﹣k2)x﹣b=0的解是x=2,④正确.
故选:C.
【点睛】本题考查一次函数的图象与一元一次方程,一次函数图象与系数的关系,一次函数的性质,解题关键是掌握一次函数与方程及不等式的关系,掌握一次函数图象与系数的关系.
6.A,B两地相距12km,甲、乙两人分别从A,B两地沿同一条公路相向而行.他们离A地的距离s(km)与时间t(h)的函数关系如图.则甲出发到相遇的时间为( )
A.1.2h B.1.5h C.1.6h D.1.8h
【点拨】根据函数图象中的数据,可以分别求得甲乙两人的速度,然后即可求得甲出发到相遇的时间.
【解析】解:由图可得,
甲的速度为:12÷3=4(km/h),
乙的速度为:12÷(3﹣1)=6(km/h),
设甲出发xh,两人相遇,
4x+6(x﹣1)=12,
解得,x=1.8,
故选:D.
【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
7.已知点P(﹣1,y1)、点Q(3,y2)在一次函数y=(2m﹣1)x+2的图象上,且y1>y2,则m的取值范围是( )
A. B. C.m≥1 D.m<1
【点拨】由题目条件可判断出一次函数的增减性,则可得到关于m的不等式,可求得m的取值范围.
【解析】解:
∵点P(﹣1,y1)、点Q(3,y2)在一次函数y=(2m﹣1)x+2的图象上,
∴当﹣1<3时,由题意可知y1>y2,
∴y随x的增大而减小,
∴2m﹣1<0,解得m<,
故选:A.
【点睛】本题主要考查一次函数的性质,得出一次函数的增减性是解题的关键.
8.如图,直线y1=ax(a≠0)与y2=x+b交于点A(﹣1,2),则下列四个结论:①a<0,b>0;②当x>0时,y1>0;③当x>﹣1时,y1<y2;④当0<y2<y1时,﹣3<x<﹣1.其中正确的结论有( )个.
A.1 B.2 C.3 D.4
【点拨】根据正比例函数和一次函数的性质,结合图象判断即可,关键是根据正比例函数和一次函数的性质判断.
【解析】解:因为y1=ax(a≠0)经过二,四象限,所以a<0,y2=x+b经过一、二、三象限,所以b>0,故①正确;
∵a<0,当x>0时,y1<0,故②错误;
结合图象可得,当x>﹣1时,直线y1=ax(a≠0)的图象在y2=x+b的图象下方,y1<y2,故③正确;
结合图象,当y2<y1时,x<﹣1,∵0<y2<y1,∴x>﹣3,∴﹣3<x<﹣1,故④正确.
故选:C.
【点睛】本题考查一次函数与一元一次不等式,正确记忆相关知识点是解题关键.
9.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲乙两队所挖管道长度都相差100米.正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
【点拨】①根据函数图象由工作效率=工作总量÷工作时间就可以得出结论;
②根据函数图象由工作效率=工作总量÷工作时间就可以得出结论;
③根据函数图象求出乙队完成的时间就可以求出结论;
④由甲的工作效率就可以求出2天时的工作量为200米,乙队是300米.6天时甲队是600米,乙队是500米得出300﹣200=600﹣500=100米故得出结论.
【解析】解:①根据函数图象得:
甲队的工作效率为:600÷6=100米/天,故①正确;
②根据函数图象,得:
乙队开挖两天后的工作效率为:(500﹣300)÷(6﹣2)=50米/天,故②正确;
③乙队完成任务的时间为:2+(600﹣300)÷50=8(天),
∴甲队提前的时间为:8﹣6=2(天).
∵2≠3,
∴③错误;
④当x=2时,甲队完成的工作量为:2×100=200米,
乙队完成的工作量为:300米.
当x=6时,甲队完成的工作量为600米,乙队完成的工作量为500米.
∵300﹣200=600﹣500=100,
∴当x=2或6时,甲乙两队所挖管道长度都相差100米,
故④正确.
∴正确的有①②④.
故选:B.
【点睛】本题考查了一次函数的图象的性质的运用,工程问题的数量关系:工作总量=工作效率×工作时间的运用,解答时分析清楚一次函数的图象的意义是关键.
10.如图,在平面直角坐标系中,直线a的解析式为,直线b的解析式为,直线a交y轴于点A,以OA为边作第一个等边三角形OAB,交直线b于点B,过点B作y轴的平行线交直线a于点A1,以为边作第二个等边三角形Δ A1BB1,交直线b于点B1,…顺次这样作下去,第2020个等边三角形的边长为( )
A.22019 B.22000 C.4038 D.4040
【点拨】延长A1B交x轴于D,A2B1交x轴于E,根据等边三角形的性质得OA=OB,A1B=BB1,A2B1=B2B1,直线b的解析式为,得∠BOD=30°,由直线a的解析式得第一个等边三角形边长为1,解Rt△OBD得,BD=1/2,把代入求得A1的纵坐标,即可求得第二个等边三角形的边长,从而找出规律,按照此规律即可求得第2020个等边三角形的边长.
【解析】解:延长A1B交x轴于D,延长A2B1交x轴于E,
∵△OAB,△BA1B1,△B1A2B2均为等边三角形,
∴OA=OB,A1B=BB1,A2B1=B2B1,
∵直线b的解析式为:,
∴∠BOD=30°,
对于直线a,,当x=0时,y=1,
∴点A的坐标为(0,1),
∴OA=OB=1,
在Rt△OBD中,OB=1,∠BOD=30°,
∴,,
∴点B的坐标为,
对于,当时,,
∴点A1的坐标为,
∴,
∴A1B=BB1=AD﹣BD=2=21,
∴OB1=OB+BB1=3,
在Rt△AB1E中,OB1=3,∠B1OE=30°,
∴,,
∴点B1的坐标为,
对于,当时,,
∴,
∴A2B1=A2E=B1E=4=22,
同理得:A3B2=23,……,
以此类推,第n个等边三角形的边长为2n﹣1,
∴第2020个等边三角形的边长为22019.
故选:A.
【点睛】本题考查了一次函数图象上点的坐标特征、等边三角形的性质,根据等边三角形的性质找出第n个等边三角形的边长为2n﹣1是解题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.函数中自变量x的取值范围是 x≥﹣2且x≠2 .
【点拨】根据二次根式的性质和分式的意义,即可求解.
【解析】解:∵分母不能为0,二次根式的被开方数为非负数,
∴x+2≥0,且2x﹣4≠0,
解得:x≥﹣2且x≠2,
故答案为:x≥﹣2且x≠2.
【点睛】本题考查了函数自变量的取值范围,解题的关键是:熟练掌握二次根式的性质和分式的意义.
12.将一次函数y=3x+1的图象沿y轴向下平移3个单位长度后,得到新的一次函数的解析式为 y=3x﹣2 .
【点拨】根据函数图象的平移规律,上加下减,可得答案.
【解析】解:由一次函数y=3x+1的图象沿y轴向下平移3个单位后,得到的图象对应的函数关系式为y=3x+1﹣3,
化简,得y=3x﹣2,
故答案为:y=3x﹣2.
【点睛】此题主要考查了一次函数图象与几何变换,求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.解析式变化的规律是:左加右减,上加下减.
13.若直线y=kx+b(k,b是常数,k≠0),过点A(3,2),则关于x的方程kx+2k+b=2的解为 x=1 .
【点拨】根据直线y=kx+b过点A(3,2),得出2=3k+b,把2=3k+b代入方程kx+2k+b=2,整理得出k(x﹣1)=0,根据k≠0,得出x﹣1=0,求出x的值即可.
【解析】解:∵直线y=kx+b过点A(3,2),
∴2=3k+b,
把2=3k+b代入kx+2k+b=2得:kx+2k+b=3k+b,
整理得:k(x﹣1)=0,
∵k≠0,
∴x﹣1=0,
解得:x=1.
故答案为:x=1.
【点睛】本题主要考查了一次函数与一元一次方程,一次函数的性质,解答本题的关键是熟练掌握一次函数的性质.
14.已知函数y=(k﹣3)x+k.
(1)该函数图象经过定点 (﹣1,3) .
(2)如果直线y=(k﹣3)x+k不经过第三象限,则k的范围是 0≤k≤3 .
【点拨】(1)根据“y=(k﹣3)x+k=k(x+1)﹣3x”来求解;
(2)由一次函数不经过第三象限可得到关于k的不等式组,则可求得k的取值范围.
【解析】解:(1)∵y=(k﹣3)x+k=k(x+1)﹣3x,
∴该函数过定点(﹣1,3).
故答案为:(﹣1,3).
(2)∵直线y=(k﹣3)x+k不经过第三象限,
∴,
解得0≤k≤3,
故答案为:0≤k≤3.
【点睛】本题考查了一次函数图象上点的坐标特征,一次函数图象与系数的关系,解答此题的关键是熟知一次函数图象上点的坐标特点,确定函数与系数之间的关系,进而求解.
15.某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kW h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 12 kW h.
【点拨】根据“电动汽车每千米的耗电量=剩余电量的减少量÷行驶路程”分别计算A、B两款新能源电动汽车每千米的耗电量,由此写出图象l1,l2的函数关系式,将x=300分别代入,求出对应函数值并计算二者之差即可.
【解析】解:A款新能源电动汽车每千米的耗电量为(80﹣48)÷200=0.16(kW h),B款新能源电动汽车每千米的耗电量为(80﹣40)÷200=0.2(kW h),
∴l1图象的函数关系式为y1=80﹣0.16x,l2图象的函数关系式为y2=80﹣0.2x,
当x=300时,y1=80﹣0.16×300=32,y2=80﹣0.2×300=20,
32﹣20=12(kW h),
∴当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多12kW h.
故答案为:12.
【点睛】本题考查一次函数的应用,根据“电动汽车每千米的耗电量=剩余电量的减少量÷行驶路程”分别计算A、B两款新能源电动汽车每千米的耗电量,由此写出图象l1,l2的函数关系式,并计算当x=300时对应函数值是解题的关键.
16.已知y1=x+a,y2=﹣2x+4a,对于任意x,m取y1与y2中较小的值,若当2a﹣2≤x≤2a时m有最大值a﹣1,则a= ﹣0.5或5 .
【点拨】分两种情况讨论,当y1>y2,则x+a>﹣2x+4a,即x>a时,当y1<y2,则x+a<﹣2x+4a,即x<a时,分别求出a的值即可.
【解析】解:当y1>y2,则x+a>﹣2x+4a,
解得:x>a,
即x>a时,m=﹣2x+4a,
∵﹣2<0,
∴m随x的增大而减小,
∴当x=2a﹣2时,m取最大值,即﹣2(2a﹣2)+4a=a﹣1,
解得:a=5,
当a=5时,2a﹣2>a,符合题意;
当y1<y2,则x+a<﹣2x+4a,
解得:x<a,
即x<a时,m=x+a,
∵1>0,
∴m随x的增大而增大,
∴当x=2a时,m取最大值,即2a+a=a﹣1,
解得:a=﹣0.5,
当a=﹣0.5时,2a<a,符合题意;
综上分析可知,a=5或﹣0.5.
故答案为:﹣0.5或5.
【点睛】本题主要考查了一次函数的性质,一元一次方程的应用,解题的关键是理解题意,能进行分类讨论解题.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.已知y﹣2与x+1成正比例函数关系,且x=﹣2时,y=6.
(1)写出y与x之间的函数关系式;
(2)求当y=4时,x的值.
【点拨】(1)根据正比例函数的定义设y﹣2=k(x+1),然后把已知的对应值代入求出k,从而得到y与x的关系式;
(2)利用(1)中的解析式得到﹣4x﹣2=4,然后解方程即可.
【解析】解:(1)根据题意,设y﹣2=k(x+1),
把x=﹣2,y=6代入得6﹣2=k×(﹣2+1),
解得k=﹣4,
∴y﹣2=﹣4(x+1),
∴y与x之间的函数关系式为y=﹣4x﹣2;
(2)当y=4时,﹣4x﹣2=4,
解得x=﹣.
【点睛】本题考查了待定系数法求一次函数解析式:求一次函数y=kx+b,则需要两组x,y的值.
18.已知一次函数y=kx+b的图象经过点(﹣1,1)和点(1,﹣5).
(1)求一次函数的表达式.
(2)求一次函数的图象与x轴的交点坐标.
【点拨】(1)把(﹣1,1)和(1,﹣5)代入y=kx+b求出k,b的值即可得出函数解析式;
(2)令y=0,求出x的值即可.
【解析】解:(1)把(﹣1,1)和(1,﹣5)代入y=kx+b得,
,
解得,
∴一次函数的表达式为y=﹣3x﹣2;
(2)当y=0时,由﹣3x﹣2=0,
解得,
∴一次函数的图象与x轴的交点坐标为.
【点睛】本题考查的是利用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,熟知利用待定系数法求一次函数解析式一般步骤是解题的关键.
19.已知函数y=(2m+1)x+m﹣3.
(1)若函数图象经过原点,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值.
【点拨】(1)根据一次函数图象上点的坐标特征,把原点坐标代入y=(2m+1)x+m﹣3可计算出m的值;
(2)根据两直线平行的问题得到2m+1=3,然后解一次方程即可.
【解析】解:(1)∵y=(2m+1)x+m﹣3经过原点,是正比例函数,
∴.
解得:m=3.
(2)∵函数的图象平行于直线y=3x﹣3,
∴2m+1=3,
解得:m=1.
【点睛】本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了一次函数图象上点的坐标特征.
20.如图,经过点(3,0)的一次函数y=﹣x+b与正比例函数y=ax交于点P(m,2).
(1)求a,b,m的值;
(2)请直接写出不等式组ax≥﹣x+b>0的解集.
【点拨】(1)将点(3,0)和点P的坐标代入一次函数的解析式求得m、b的值,然后将点P的坐标代入正比例函数即可求得a的值;
(2)直接根据函数的图象结合点P的坐标确定不等式的解集即可.
【解析】解:(1)∵经过点(3,0)的一次函数y=﹣x+b与正比例函数y=ax交于点P(m,2).
∴﹣3+b=0,
∴b=3,
∴y=﹣x+3,
∴2=﹣m+3,
∴m=1,
∴P(1,2),
∴a=2.
(2)观察图象得:不等式组ax≥﹣x+b>0的解集为1≤x<3.
【点睛】考查了一次函数与一元一次不等式的问题,解题的关键是能够确定有关待定系数的值,难度不大.
21.如图,直线y1=2x﹣2的图象与y轴交于点A,直线y2=﹣2x+6的图象与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 1<x<3 ;
(3)求△ABC的面积.
【点拨】(1)根据题意画出图象,利用其交点坐标得出方程组的解;
(2)利用函数图象得出在x轴上方时,对应x的取值范围;
(3)利用已知图象结合三角形面积求法得出答案.
【解析】解:(1)如图所示:方程组组的解为:;
故答案为:;
(2)如图所示:当y1>0与y2>0同时成立时,
x取何值范围是:1<x<3;
故答案为:1<x<3;
(3)∵令x=0,则y1=﹣2,y2=6,
∴A(0,﹣2),B(0,6).
∴AB=8.
∴S△ABC=×8×2=8.
【点睛】此题主要考查了一次函数与二元一次方程组以及一次函数与一元一次不等式和三角形面积求法等知识,正确利用数形结合分析是解题关键.
22.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港停止.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的关系如图所示.
(1)B、C两港口间的距离为 90 km,a= 2 ;
(2)甲船出发几小时追上乙船?
(3)在整个过程中,什么时候甲乙两船相距10km?
【点拨】(1)由甲船行驶的函数图象可以看出,甲船从A港出发,0.5h后到达B港,a h后到达C港,又由于甲船行驶速度不变,则可以求出a的值;
(2)分别求出0.5h后甲乙两船行驶的函数表达式,联立即可求解;
(3)分三种情形分别求解即可解决问题;
【解析】解:(1)B、C两港口间距离s=90(km),
又由于甲船行驶速度不变,
故30÷0.5=60(km/h),
则a=2(h).
故答案为:90,2;
(2)由点(3,90)求得,y2=30x.
当0.5<x≤2时,设解析式为y1=ax+c,
由点(0.5,0),(2,90)在图象上,
∴,
解得:,
∴y1=60x﹣30,
当y1=y2时,60x﹣30=30x,解得,x=1.
此时y1=y2=30.
所以点P的坐标为(1,30);
(3)当甲船还未追上乙船时,30x﹣(60x﹣30)=10.
解:x=
②当Ψ船追上乙船后,当未到达C港口时:(60x﹣30)﹣30x=10.解得:x=,
③当甲船到达C港口,乙船还未到达C港口时:90﹣30x=10.
解得:x=
综上:当经过或或时,甲乙两船相距10km.
【点睛】此题主要考查了一次函数的应用以及函数方程、函数图象与实际结合的问题,利用数形结合得出关键点坐标是解题关键.
23.如图,直线y=kx﹣3与x轴,y轴分别交于B,C两点,其中OB=1.
(1)求k的值;
(2)若点A(x,y)是第一象限内的直线y=kx﹣3上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)探索:
①点D是直线y=kx﹣3上的一个动点,当△OBD的面积是3时,求点D的坐标;
②在①的条件下,且点D在第一象限,问:x轴上是否存在一点P,使△POD等腰三角形?若存在,请直接写出满足条件的所有P点的坐标;若不存在,请说明理由.
【点拨】(1)由OB=1可得出点B坐标,将点B的坐标代入直线解析式中即可得出k;
(2)直接利用三角形的面积公式即可得出结论;
(3)①当△OBD的面积是3时,则△OBD的高为6,即点D到x轴距离为6,据此求解即可;
②设出点P的坐标,进而利用两点间的距离公式求出OD2,OP2,DP2,分三种情况用两边相等建立方程求解即可.
【解析】解:(1),直线y=kx﹣3与x轴,y轴分别交于B,C两点,其中OB=1,
∴B(1,0),
交点B的坐标代入y=kx﹣3中,得:
k﹣3=0,
解得k=3,
∴y=3x﹣3,
∴k的值为3;
(2)∵点A(x,y)是第一象限内的直线y=3x﹣3上的一个动点,
∴△AOB的面积;
(3)①∵△OBD的面积是3,OB=1,
∴△OBD的高为6,
∴点D到x轴距离为6,
∵点D是直线y=3x﹣3上的一个动点,
∴y=3x﹣3=6时,x=3,
y=3x﹣3=﹣6时,x=﹣1,
∴点D的坐标为(3,6)或(﹣1,﹣6);
②x轴上存在一点P,使△POD等腰三角形;理由如下:
∵在①的条件下,且点D在第一象限,
∴点D的坐标为(3,6),
设点P(m,0),
∴OD2=32+62=45,OP2=m2,DP2=(m﹣3)2+36,
∵△DOP为等腰三角形,
∴当OD=OP时,OD2=OP2,即:45=m2,
解得,
此时点P坐标为,;
当OD=DP时,OD2=DP2,即:45=(m﹣3)2+36,
解得m=0(此时和点A重合,舍去)或m=6,
此时点P坐标为(6,0);
当OP=DP时,OP2=DP2,即:m2=(m﹣3)2+36,
解得,
此时点P坐标为;
即:满足条件的P点坐标为,,(6,0),.
【点睛】此题是一次函数综合题,主要考查了一次函数的图象与性质,待定系数法,三角形的面积公式,等腰三角形的性质,解答本题的关键是熟练掌握一次函数的性质.
24.【问题背景】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的.
【实验操作】为了解某品牌新能源汽车电池需要多久能充满,以及充满电量状态下新能源汽车的最大行驶里程,某综合实践小组设计两组实验.
实验一:探究电池充电状态下新能源汽车仪表盘增加的电量y(%)与时间t(分钟)的关系,数据记录如表1:
电池充电状态
时间t(分钟) 0 10 30 60
增加的电量y(%) 0 10 30 60
实验二:探究充满电量状态下新能源汽车行驶过程中仪表盘显示电量e(%)与行驶里程s(千米)的关系,数据记录如表2:
新能源汽车行驶过程
已行驶里程s(千米) 0 160 200 280
显示电量e(%) 100 60 50 30
【建立模型】(1)观察表1、表2发现都是一次函数模型,请结合表1、表2的数据,求出y关于t的函数解析式及e关于s的函数解析式:
【解决问题】(2)该品牌新能源汽车在充满电量的状态下出发,前往距离出发点500千米处的目的地,若新能源汽车行驶280千米后,在途中的服务区充电30分钟,充电后该新能源汽车是否有足够的电量行驶到目的地.
【点拨】(1)根据表1中数据变化规律直接写出y关于t的函数解析式,利用待定系数法求出e关于s的函数解析式即可;
(2)将s=280代入e关于s的函数解析式,求出剩余电量;将t=30代入y关于t的函数解析式,求出充入的电量,从而求出在途中的服务区充电30分钟后仪表盘显示的电量,将它代入e关于s的函数解析式,求出能够行驶的距离并与剩余的路程相比即可得出结论.
【解析】解:(1)由表格中的数据可知,y关于t的函数解析式为:y=t;
设e关于s的函数解析式为e=k2s+b(k2、b为常数,且k2≠0),
将s=0,e=100和s=160,e=6(0分)别代入e=k2s+b,
得,
解得,
∴e关于s的函数解析式为:e=﹣s+100;
(2)当s=280时,e=﹣×280+100=30,
当t=30时,y=30,
30+30=60,
∴在途中的服务区充电30分钟后,仪表盘显示电量是60%.
当e=60时,60=﹣s+100,解得s=160,
∴当仪表盘显示电量为60%时还能行驶160千米.
剩余路程为500﹣280=220(千米),
∵160<220,
∴充电后该新能源汽车没有足够的电量行驶到目的地.
【点睛】本题考查了函数关系式,函数值,掌握待定系数法求函数的解析式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
