浙江省嘉兴市2024-2025学年上学期“南中杯”数学学科素养与创新能力竞赛九年级试卷(含答案)
文档属性
| 名称 | 浙江省嘉兴市2024-2025学年上学期“南中杯”数学学科素养与创新能力竞赛九年级试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 241.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 00:00:00 | ||
图片预览


文档简介
2024.11 嘉兴 “南中杯” 数学学科素养与创新能力竞赛
一、选择题 (每小题 3 分, 共 24 分)
1.已知 ,则下列等式中正确的是( )
A. B. C. D.
2. 若把抛物线 向右平移 2 个单位,所得抛物 线的表达式为( )
A. B. C. D.
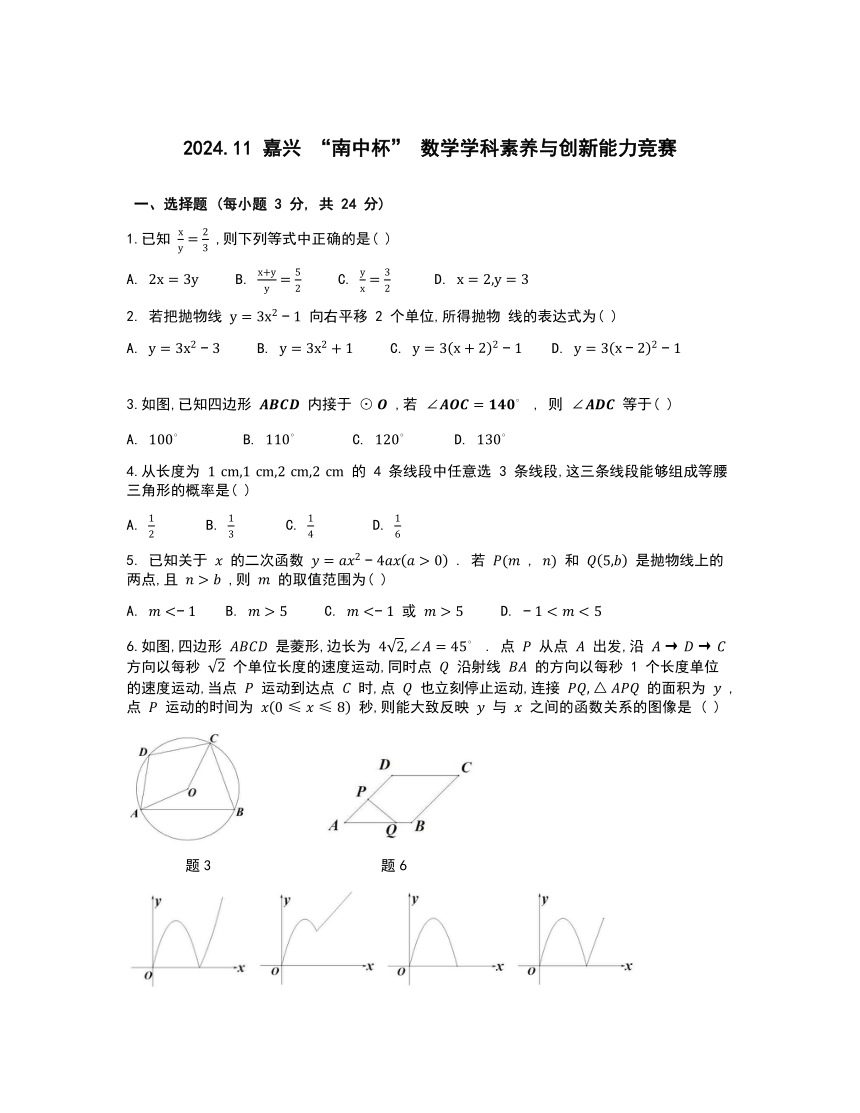
3.如图,已知四边形 内接于 ,若 , 则 等于( )
A. B. C. D.
4.从长度为 的 4 条线段中任意选 3 条线段,这三条线段能够组成等腰三角形的概率是( )
A. B. C. D.
5. 已知关于 的二次函数 . 若 , 和 是抛物线上的两点,且 ,则 的取值范围为( )
A. B. C. 或 D.
6.如图,四边形 是菱形,边长为 . 点 从点 出发,沿 方向以每秒 个单位长度的速度运动,同时点 沿射线 的方向以每秒 1 个长度单位的速度运动,当点 运动到达点 时,点 也立刻停止运动,连接 的面积为 ,点 运动的时间为 秒,则能大致反映 与 之间的函数关系的图像是 ( )
题3 题6
B. C. D.
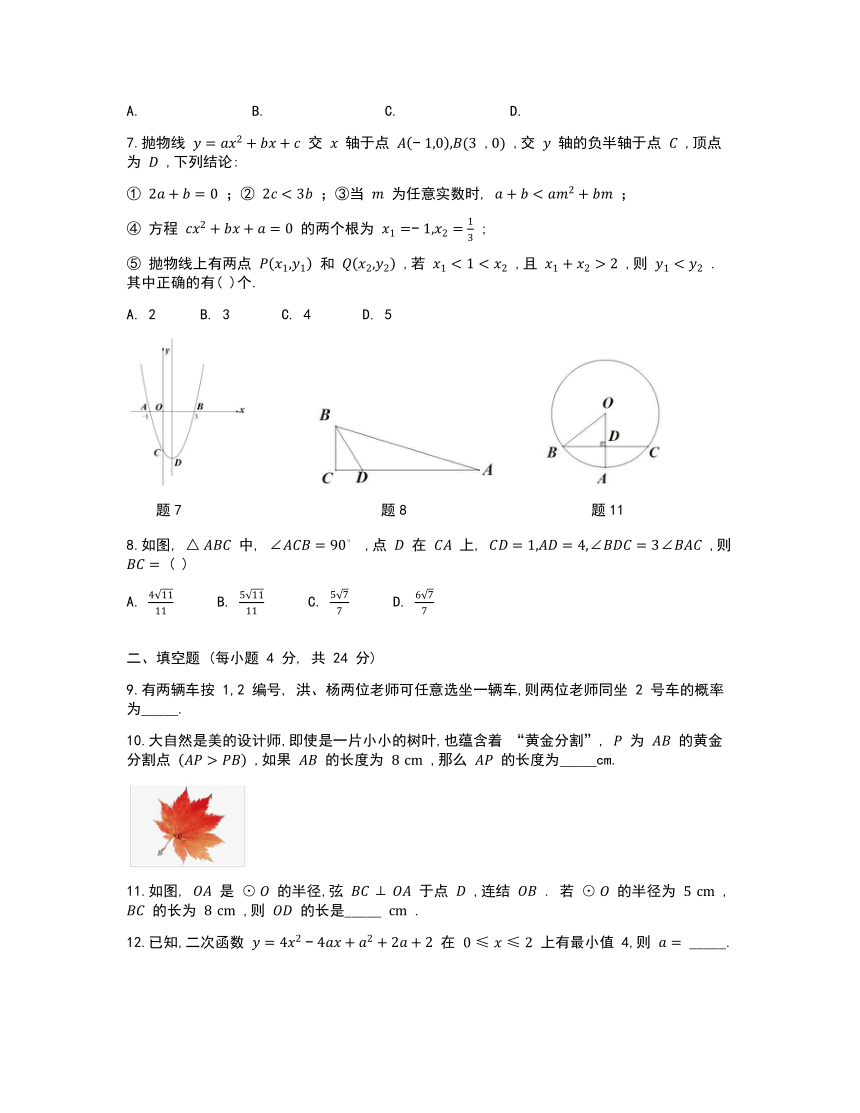
7.抛物线 交 轴于点 , ,交 轴的负半轴于点 ,顶点为 ,下列结论:
① ;② ;③当 为任意实数时, ;
④ 方程 的两个根为 ;
⑤ 抛物线上有两点 和 ,若 ,且 ,则 . 其中正确的有( )个.
A. 2 B. 3 C. 4 D. 5
题7 题8 题11
8.如图, 中, ,点 在 上, ,则 ( )
A. B. C. D.
二、填空题 (每小题 4 分, 共 24 分)
9.有两辆车按 1,2 编号, 洪、杨两位老师可任意选坐一辆车,则两位老师同坐 2 号车的概率为_____.
10.大自然是美的设计师,即使是一片小小的树叶,也蕴含着 “黄金分割”, 为 的黄金分割点 ,如果 的长度为 ,那么 的长度为_____cm.
11.如图, 是 的半径,弦 于点 ,连结 . 若 的半径为 , 的长为 ,则 的长是_____ .
12.已知,二次函数 在 上有最小值 4,则 _____.
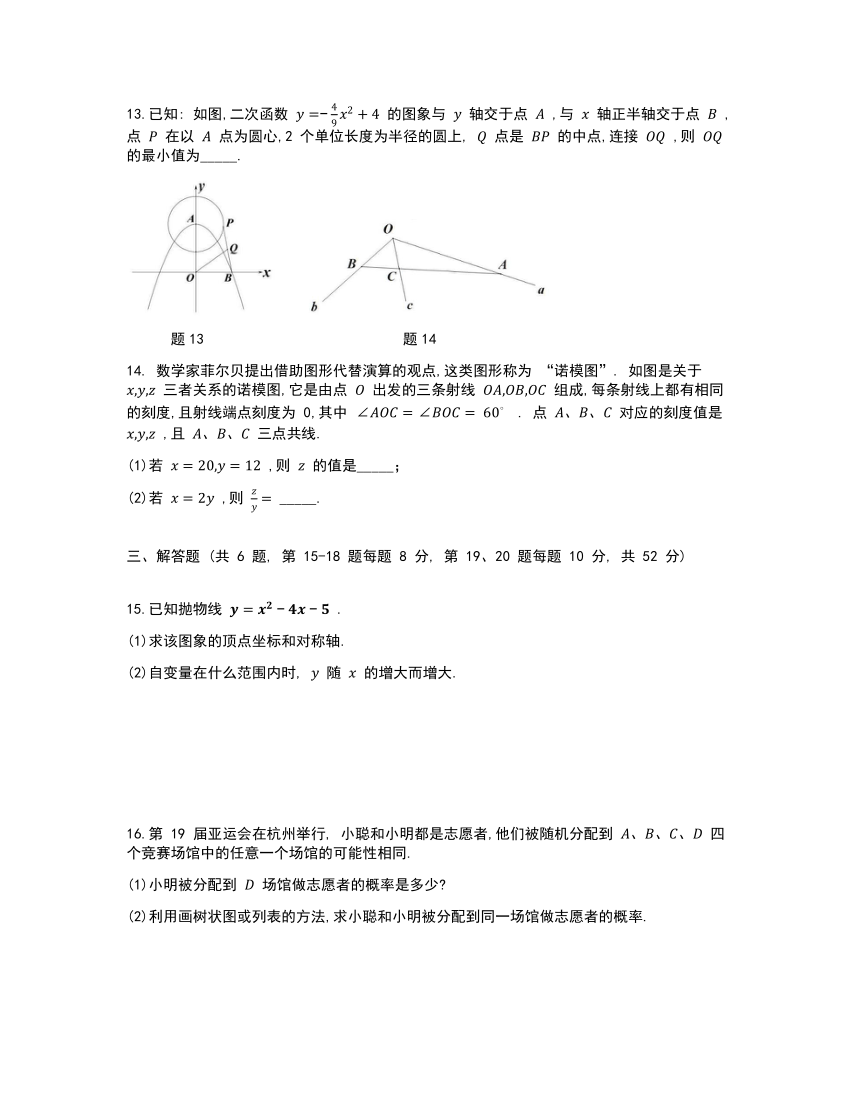
13.已知: 如图,二次函数 的图象与 轴交于点 ,与 轴正半轴交于点 ,点 在以 点为圆心,2 个单位长度为半径的圆上, 点是 的中点,连接 ,则 的最小值为_____.
题13 题14
数学家菲尔贝提出借助图形代替演算的观点,这类图形称为 “诺模图”. 如图是关于 三者关系的诺模图,它是由点 出发的三条射线 组成,每条射线上都有相同的刻度,且射线端点刻度为 0,其中 . 点 对应的刻度值是 ,且 三点共线.
(1)若 ,则 的值是_____;
(2)若 ,则 _____.
三、解答题 (共 6 题, 第 15-18 题每题 8 分, 第 19、20 题每题 10 分, 共 52 分)
15.已知抛物线 .
(1)求该图象的顶点坐标和对称轴.
(2)自变量在什么范围内时, 随 的增大而增大.
16.第 19 届亚运会在杭州举行, 小聪和小明都是志愿者,他们被随机分配到 四个竞赛场馆中的任意一个场馆的可能性相同.
(1)小明被分配到 场馆做志愿者的概率是多少
(2)利用画树状图或列表的方法,求小聪和小明被分配到同一场馆做志愿者的概率.
17.如图,在直角坐标系中, 各顶点的坐标如下: .
(1)以原点 为位似中心,在 轴上方作与 的位似比为 2 的位似图形 .
(2)顶点 的坐标为_____, 与 的面积之比为_____.
18.在如图所示的方格纸中存在 ,其中,点 , 均在格点上.
(1)用直尺作出 的外接圆圆心 .
(2)若方格纸中每个小正方形的边长为 1,求 外接圆半径 的长.
(3)在(2)的条件下,求出弧 的长度.
19.某超市购进甲、乙两种商品,已知购进 3 件甲商品和 2 件乙商品, 需 60 元; 购进 2 件甲商品和 3 件乙商品, 需 65 元.
(1)甲、乙两种商品的进货单价分别是多少?
(2)设甲商品的销售单价为 (单位:元/件),在销售过程中发现,当 时,甲商品的日销售量 (单位: 件) 与销售单价 之间存在一次函数关系, 之间的部分数值对应关系如表:
销售单价 (元/件) 11 19
日销售量 (件) 18 2
请写出当 时, 与 之间的函数关系式.
在(2)的条件下,设甲商品的日销售利润为 元,当甲商品的销售单价 (元/件) 定为多少时, 日销售利润最大 最大利润是多少
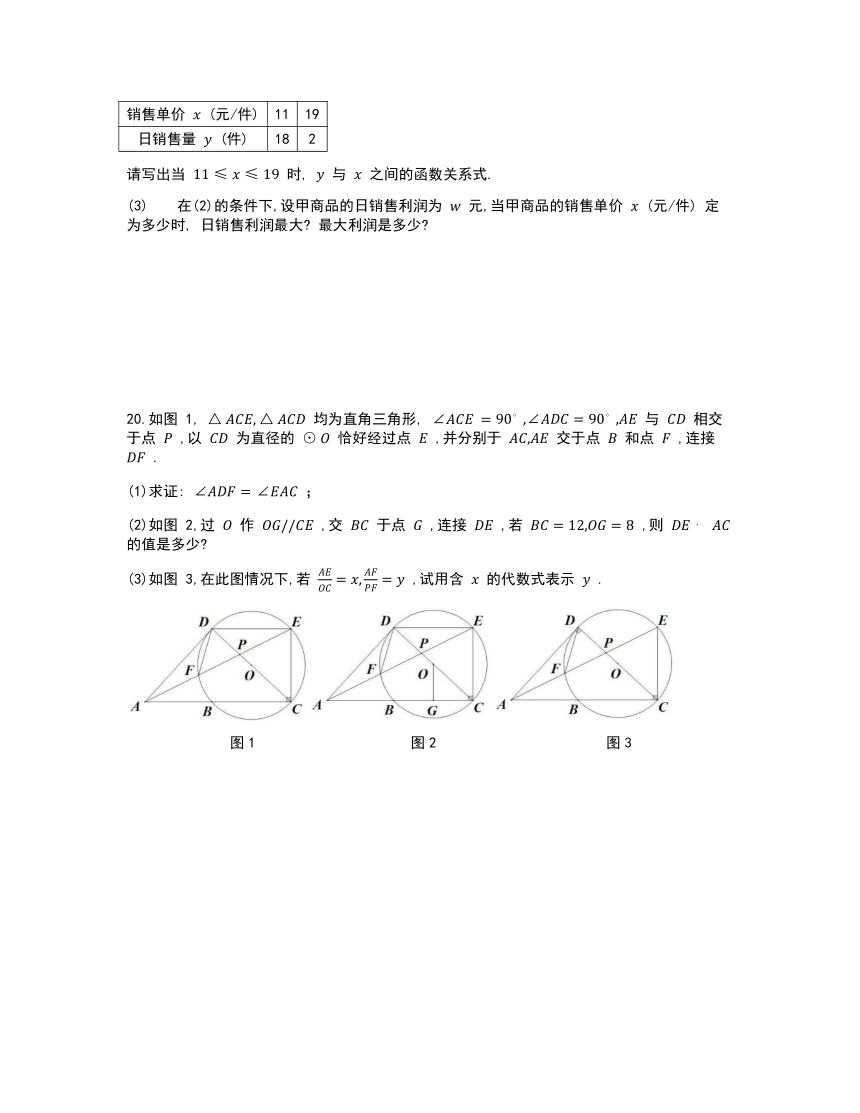
20.如图 1, 均为直角三角形, 与 相交于点 ,以 为直径的 恰好经过点 ,并分别于 交于点 和点 ,连接 .
(1)求证: ;
(2)如图 2,过 作 ,交 于点 ,连接 ,若 ,则 的值是多少
(3)如图 3,在此图情况下,若 ,试用含 的代数式表示 .
图1 图2 图3
解析
选C
依据“左加右减”选D
由同弧所对的圆周角等于圆心角的一半得 ,又由圆内接四边形 得 ,故 ,选 B.
从四条线段中任意取三条等价于从四条线段中拿出一条作为没被取的, 故总共有 4 种取法, 要满足所取线段能构成等腰三角形就需要所取的三条线段中有两条 的线段或两条 的线段,而取两条 的线段时所取的第三条线段一定是 ,而 ,所以此时无法组成三角形,故所取的三条线段能组成等腰三角形的概率 ,选 A.
由题意得: 抛物线开口向上,对称轴 ,根据二次函数的对称性,当 时, 或 5,故当 时, 或 ,选 C.
显然点 到 的距离 ,①当 时,此时 ,② 当 时,此时 ,③当 时,此时 ,故能大致反映 与 之间的函数关系的图像是 D.
由于抛物线经过点(-1,0)和(3,0),则其对称轴为直线 ,即 ,故 ,故①正确; 由抛物线的对称轴为直线 知其在 时取到最小值,故对任意 ,即 ,故③错误; 由两点式得 ,故 ,故 ,故②错误,故 ,即 ,故④正确; 由 知点 在直线 左侧,点 在直线 右侧,又 ,故 ,又抛物线开口向上,且对称轴为直线 ,由轴距法得 ,故⑤正确,所以正确的一共有 3 个,选 B.
设 ,显然 ,由合角公式得: ,
,解得 ,选 C.
由黄金分割点定义知 .
3
显然,二次函数开口向上,且对称轴为 ,当 时,即 ,当 时, ,解得 或 (舍);当 时,即 ,当 时, ,解得 ;当 时,即 ,
当 时, ,方程无解;故答案为 1 或 .
连结 ,取 中点 ,连结 ,因为 ,因此 , ,当且仅当 三点共线时取等号.
方法一: 对于 (1),过点 作 的垂线交 延长线于点 ,
,因此 ;
为 的角平分线,
,
,
由斯特瓦尔特定理,当 为 的角平分线时,
,
因此 ;
对于 (2),同 (1) 可得 .
方法二: 过点 作 交 于点 ,
依题意得, ,
.
,
为等边三角形.
,
,
,
,
,
即 ,得 .
(1)当 时,代入上式得 ;
(2) 时,即 ,从而 .
(1)
分析: 主要考察抛物线的基本知识和图像.
(1)
(1)略;(2)(一2,2),4:1
分析: 主要考察位似三角形的基本定义.
(1) 略; (2) (3)
分析: (1) (2) 问主要考察外心的简单性质以及勾股定理.
(3)问主要考察“一线三等角模型”发现弧 所对圆心角为
19. (1) 10,15 ;
(2) ;
(3) ,当 时,利润最大, 最大利润为 50 元.
20. (1)见解答;(2)400;(3)
分析: 本题主要考察圆中角的关系, 导角即可.
(1)证明: ,
,
,
.
(2)分析: 本题主要考察相似关系,由题意把着眼点放在 和 上,不难发现包含这两条边的 和 具有相似关系,进而可以得到 ,题目就转化为求 的长,这样就容易解得了. (当然读者也可以分别求出 和 的长,不过这样就显得有些繁琐了, 这应该并不是出题人想看到的) 过程如下:
,
,
,
,
,
,
,
,
,
,
的值是 400.
(3)分析: 本题主要考察相似关系的综合运用. 粗看 和 ,其形式似乎并不好,我们不太能找到相应的相似三角形将他们挂钩起来,但是如果把 转化为 ,考虑边 和 关系就会好做一些.过程如下:
连结 ,则 ,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
一、选择题 (每小题 3 分, 共 24 分)
1.已知 ,则下列等式中正确的是( )
A. B. C. D.
2. 若把抛物线 向右平移 2 个单位,所得抛物 线的表达式为( )
A. B. C. D.
3.如图,已知四边形 内接于 ,若 , 则 等于( )
A. B. C. D.
4.从长度为 的 4 条线段中任意选 3 条线段,这三条线段能够组成等腰三角形的概率是( )
A. B. C. D.
5. 已知关于 的二次函数 . 若 , 和 是抛物线上的两点,且 ,则 的取值范围为( )
A. B. C. 或 D.
6.如图,四边形 是菱形,边长为 . 点 从点 出发,沿 方向以每秒 个单位长度的速度运动,同时点 沿射线 的方向以每秒 1 个长度单位的速度运动,当点 运动到达点 时,点 也立刻停止运动,连接 的面积为 ,点 运动的时间为 秒,则能大致反映 与 之间的函数关系的图像是 ( )
题3 题6
B. C. D.
7.抛物线 交 轴于点 , ,交 轴的负半轴于点 ,顶点为 ,下列结论:
① ;② ;③当 为任意实数时, ;
④ 方程 的两个根为 ;
⑤ 抛物线上有两点 和 ,若 ,且 ,则 . 其中正确的有( )个.
A. 2 B. 3 C. 4 D. 5
题7 题8 题11
8.如图, 中, ,点 在 上, ,则 ( )
A. B. C. D.
二、填空题 (每小题 4 分, 共 24 分)
9.有两辆车按 1,2 编号, 洪、杨两位老师可任意选坐一辆车,则两位老师同坐 2 号车的概率为_____.
10.大自然是美的设计师,即使是一片小小的树叶,也蕴含着 “黄金分割”, 为 的黄金分割点 ,如果 的长度为 ,那么 的长度为_____cm.
11.如图, 是 的半径,弦 于点 ,连结 . 若 的半径为 , 的长为 ,则 的长是_____ .
12.已知,二次函数 在 上有最小值 4,则 _____.
13.已知: 如图,二次函数 的图象与 轴交于点 ,与 轴正半轴交于点 ,点 在以 点为圆心,2 个单位长度为半径的圆上, 点是 的中点,连接 ,则 的最小值为_____.
题13 题14
数学家菲尔贝提出借助图形代替演算的观点,这类图形称为 “诺模图”. 如图是关于 三者关系的诺模图,它是由点 出发的三条射线 组成,每条射线上都有相同的刻度,且射线端点刻度为 0,其中 . 点 对应的刻度值是 ,且 三点共线.
(1)若 ,则 的值是_____;
(2)若 ,则 _____.
三、解答题 (共 6 题, 第 15-18 题每题 8 分, 第 19、20 题每题 10 分, 共 52 分)
15.已知抛物线 .
(1)求该图象的顶点坐标和对称轴.
(2)自变量在什么范围内时, 随 的增大而增大.
16.第 19 届亚运会在杭州举行, 小聪和小明都是志愿者,他们被随机分配到 四个竞赛场馆中的任意一个场馆的可能性相同.
(1)小明被分配到 场馆做志愿者的概率是多少
(2)利用画树状图或列表的方法,求小聪和小明被分配到同一场馆做志愿者的概率.
17.如图,在直角坐标系中, 各顶点的坐标如下: .
(1)以原点 为位似中心,在 轴上方作与 的位似比为 2 的位似图形 .
(2)顶点 的坐标为_____, 与 的面积之比为_____.
18.在如图所示的方格纸中存在 ,其中,点 , 均在格点上.
(1)用直尺作出 的外接圆圆心 .
(2)若方格纸中每个小正方形的边长为 1,求 外接圆半径 的长.
(3)在(2)的条件下,求出弧 的长度.
19.某超市购进甲、乙两种商品,已知购进 3 件甲商品和 2 件乙商品, 需 60 元; 购进 2 件甲商品和 3 件乙商品, 需 65 元.
(1)甲、乙两种商品的进货单价分别是多少?
(2)设甲商品的销售单价为 (单位:元/件),在销售过程中发现,当 时,甲商品的日销售量 (单位: 件) 与销售单价 之间存在一次函数关系, 之间的部分数值对应关系如表:
销售单价 (元/件) 11 19
日销售量 (件) 18 2
请写出当 时, 与 之间的函数关系式.
在(2)的条件下,设甲商品的日销售利润为 元,当甲商品的销售单价 (元/件) 定为多少时, 日销售利润最大 最大利润是多少
20.如图 1, 均为直角三角形, 与 相交于点 ,以 为直径的 恰好经过点 ,并分别于 交于点 和点 ,连接 .
(1)求证: ;
(2)如图 2,过 作 ,交 于点 ,连接 ,若 ,则 的值是多少
(3)如图 3,在此图情况下,若 ,试用含 的代数式表示 .
图1 图2 图3
解析
选C
依据“左加右减”选D
由同弧所对的圆周角等于圆心角的一半得 ,又由圆内接四边形 得 ,故 ,选 B.
从四条线段中任意取三条等价于从四条线段中拿出一条作为没被取的, 故总共有 4 种取法, 要满足所取线段能构成等腰三角形就需要所取的三条线段中有两条 的线段或两条 的线段,而取两条 的线段时所取的第三条线段一定是 ,而 ,所以此时无法组成三角形,故所取的三条线段能组成等腰三角形的概率 ,选 A.
由题意得: 抛物线开口向上,对称轴 ,根据二次函数的对称性,当 时, 或 5,故当 时, 或 ,选 C.
显然点 到 的距离 ,①当 时,此时 ,② 当 时,此时 ,③当 时,此时 ,故能大致反映 与 之间的函数关系的图像是 D.
由于抛物线经过点(-1,0)和(3,0),则其对称轴为直线 ,即 ,故 ,故①正确; 由抛物线的对称轴为直线 知其在 时取到最小值,故对任意 ,即 ,故③错误; 由两点式得 ,故 ,故 ,故②错误,故 ,即 ,故④正确; 由 知点 在直线 左侧,点 在直线 右侧,又 ,故 ,又抛物线开口向上,且对称轴为直线 ,由轴距法得 ,故⑤正确,所以正确的一共有 3 个,选 B.
设 ,显然 ,由合角公式得: ,
,解得 ,选 C.
由黄金分割点定义知 .
3
显然,二次函数开口向上,且对称轴为 ,当 时,即 ,当 时, ,解得 或 (舍);当 时,即 ,当 时, ,解得 ;当 时,即 ,
当 时, ,方程无解;故答案为 1 或 .
连结 ,取 中点 ,连结 ,因为 ,因此 , ,当且仅当 三点共线时取等号.
方法一: 对于 (1),过点 作 的垂线交 延长线于点 ,
,因此 ;
为 的角平分线,
,
,
由斯特瓦尔特定理,当 为 的角平分线时,
,
因此 ;
对于 (2),同 (1) 可得 .
方法二: 过点 作 交 于点 ,
依题意得, ,
.
,
为等边三角形.
,
,
,
,
,
即 ,得 .
(1)当 时,代入上式得 ;
(2) 时,即 ,从而 .
(1)
分析: 主要考察抛物线的基本知识和图像.
(1)
(1)略;(2)(一2,2),4:1
分析: 主要考察位似三角形的基本定义.
(1) 略; (2) (3)
分析: (1) (2) 问主要考察外心的简单性质以及勾股定理.
(3)问主要考察“一线三等角模型”发现弧 所对圆心角为
19. (1) 10,15 ;
(2) ;
(3) ,当 时,利润最大, 最大利润为 50 元.
20. (1)见解答;(2)400;(3)
分析: 本题主要考察圆中角的关系, 导角即可.
(1)证明: ,
,
,
.
(2)分析: 本题主要考察相似关系,由题意把着眼点放在 和 上,不难发现包含这两条边的 和 具有相似关系,进而可以得到 ,题目就转化为求 的长,这样就容易解得了. (当然读者也可以分别求出 和 的长,不过这样就显得有些繁琐了, 这应该并不是出题人想看到的) 过程如下:
,
,
,
,
,
,
,
,
,
,
的值是 400.
(3)分析: 本题主要考察相似关系的综合运用. 粗看 和 ,其形式似乎并不好,我们不太能找到相应的相似三角形将他们挂钩起来,但是如果把 转化为 ,考虑边 和 关系就会好做一些.过程如下:
连结 ,则 ,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
