第3章 圆 单元检测能力提升卷(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
第3章 圆 单元检测能力提升卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=25°,则∠AOC的大小是( )
A.25° B.50° C.65° D.75°
2.下列说法中正确的是( )
A.所对圆心角相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
3.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
4.如图,△ABC中,∠A=50°,以AB为直径的⊙O分别与BC,AC交于点D,E,且BD=CD,连接BE,DE,则∠BED的大小为( )
A.25° B.30° C.35° D.50°
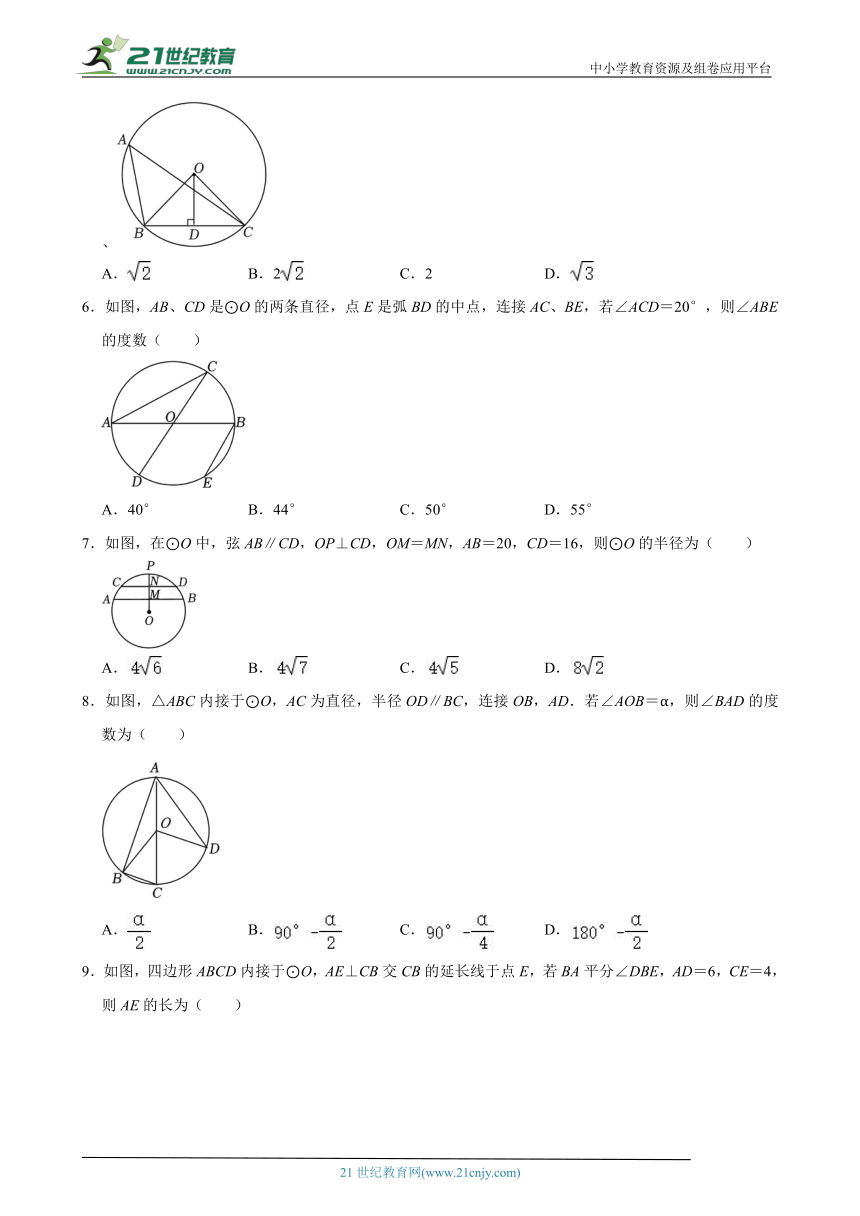
5.如图,点A在⊙O上,OD⊥弦BC于点D.若∠BAC=45°,OD=1,则BC=( )
、
A. B.2 C.2 D.
6.如图,AB、CD是⊙O的两条直径,点E是弧BD的中点,连接AC、BE,若∠ACD=20°,则∠ABE的度数( )
A.40° B.44° C.50° D.55°
7.如图,在⊙O中,弦AB∥CD,OP⊥CD,OM=MN,AB=20,CD=16,则⊙O的半径为( )
A. B. C. D.
8.如图,△ABC内接于⊙O,AC为直径,半径OD∥BC,连接OB,AD.若∠AOB=α,则∠BAD的度数为( )
A. B. C. D.
9.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=6,CE=4,则AE的长为( )
A.2 B.3 C. D.
10.如图在给定的⊙O中,弦AB的弦心距OH=6,CD=16,点E在弦CD上,且OE=ED=5,当△EAB面积的为最大时,DH的长为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.在半径为6的圆中,60°的圆心角所对的弧长为 .
12.在Rt△ABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的直径是 .
13.如图,在半径为10cm的⊙O中,AB=16cm,OC⊥AB于点C,则OC等于 cm.
14.半径为3的正六边形内接于⊙O,则正六边形的边长为 .
15.如图,等腰△ABC内接于⊙O,AB=AC,点D为劣弧BC上一点,∠ADC=60°,若CD=2BD=4,则四边形ABDC的面积为 .
16.如图,在半圆O中,直径AB=8,C,D是半圆上两点,P是直径上一点,若∠AOC=48°,∠AOD=72°,则PC+PD的最小值为 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,⊙O的弦AB,CD相交于点E,且AB=CD,求证:EB=ED.
18.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣1,3),B(﹣3,0),C(﹣1,0),把△ABC绕点C按顺时针方向旋转90°后得到△A1B1C.(每个方格的边长均为1个单位)
(1)画出△A1B1C并直接写出:
A1的坐标为 ,
B1的坐标为 ;
(2)判断直线AB与直线A1B1的位置关系为 .
19.如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°.
(1)求∠CAD的度数;
(2)若⊙O的半径为1,求图中阴影部分的面积.
20.如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接BC,作OF⊥BC于点F,求OF的长.
21.如图,四边形ABCD内接于一圆,连结AC、BD.
(1)若∠DAB=60°,∠ACB=70°,求∠ABD的度数.
(2)若AC为直径,C为的中点,请探究∠DAB与∠ACB之间的关系.
22.如图,在半圆O中,直径AB=6,点C在上,连接BC,弦BD平分∠ABC,连接OD.
(1)求证:OD∥BC;
(2)连接OC,AD.若OC∥AD,求BD的长.
23.在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交直线AC于点E,连结BE.
小明:根据题意,我画出了如图1的情况;
小丽:小明,你的思考不够全面,我认为还有其他的情况,若∠BAC为钝角,我发现圆与直线AC的交点在线段CA的延长线上;
小明:哦...我明白了!
(1)在图1中求证:点D是边BC的中点;
(2)记∠ABE的度数为α.求出∠C的度数(用α表示).
24.已知AB是⊙O的直径,点C在⊙O上,D为弧BC的中点.
(1)如图①,连接AC,AD,OD.求证:OD∥AC;
(2)如图②,过点D作DE⊥AB交⊙O于点E,直径EF交AC于点G,若G为AC中点,
①求证:∠BOD=45°;
②若⊙O的半径为2,求AC的长.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=25°,则∠AOC的大小是( )
A.25° B.50° C.65° D.75°
【点拨】利用圆周角定理解决问题即可.
【解析】解:∵∠AOC=2∠ABC,∠ABC=25°,
∴∠AOC=50°,
故选:B.
【点睛】本题考查圆周角定理,解题的关键是记住在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2.下列说法中正确的是( )
A.所对圆心角相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
【点拨】根据等弧的定义垂径定理,圆周角定理一一判断即可.
【解析】解:A.在同圆或等圆中,所对圆心角相等的两条弧是等弧,故A错误,本选项不符合题意;
B.平分弦的直径垂直于弦,此弦不能是直径,故B错误,本选项不符合题意;
C.在同圆或等圆中,相等的圆心角所对的弧相等,故C错误,本选项不符合题意;
D.经过圆心的每一条直线都是圆的对称轴,故D正确,本选项符合题意.
故选:D.
【点睛】本题考查圆周角定理,垂径定理,轴对称等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
3.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
【点拨】连接OA,OB,根据圆周角定理得到∠AOB=2∠ADB=36°,于是得到结论.
【解析】解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数==10,
故选:A.
【点睛】本题考查了正多边形与圆,圆周角定理,正确的理解题意是解题的关键.
4.如图,△ABC中,∠A=50°,以AB为直径的⊙O分别与BC,AC交于点D,E,且BD=CD,连接BE,DE,则∠BED的大小为( )
A.25° B.30° C.35° D.50°
【点拨】连接AD,证明AB=AC,利用三线合一的性质求出∠BAD即可解决问题.
【解析】解:连接AD,
∵AB是直径,
∴∠ADB=90°,即AD⊥BC,
∵BD=DC,
∴AB=AC,
∴∠BAD=∠BAC=25°,
∴∠BED=∠BAD=25°.
故选:A.
【点睛】本题考查圆周角定理,等腰三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.如图,点A在⊙O上,OD⊥弦BC于点D.若∠BAC=45°,OD=1,则BC=( )
A. B.2 C.2 D.
【点拨】利用圆周角定理得到∠BOC=90°,利用等腰三角形的性质得∠OBC=∠OCB=45°,再根据垂径定理得到BD=CD,根据等腰三角形的判定与性质求出BD,从而得到BC的长.
【解析】解:∵∠BAC=45°,
∴∠BOC=2∠BAC=2×45°=90°,
∵OB=OC,
∴∠OBC=∠OCB=45°,
∵OD⊥BC,
∴BD=CD,∠BOD=180°﹣90°﹣45°=45°=∠OBD,
∴BD=OD=2,
∴BC=2BD=2.
故选:C.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.
6.如图,AB、CD是⊙O的两条直径,点E是弧BD的中点,连接AC、BE,若∠ACD=20°,则∠ABE的度数( )
A.40° B.44° C.50° D.55°
【点拨】连接OE,利用圆周角定理求得∠AOD=40°,再求得∠DOE=∠BOE=70°,根据等边对等角即可求解.
【解析】解:连接OE,如图所示:
∵∠ACD=20°,
∴∠AOD=2∠ACD=40°,
∵点E是弧BD的中点,
∴,
∵OE=OB,
∴,
故选:D.
【点睛】本题主要考查圆周角定理及等腰三角形的判定和性质,熟练掌握圆周角定理是解题的关键.
7.如图,在⊙O中,弦AB∥CD,OP⊥CD,OM=MN,AB=20,CD=16,则⊙O的半径为( )
A. B. C. D.
【点拨】如图,连接OA,OC.设OA=OC=r,OM=MN=a,构建方程组求出r即可.
【解析】解:如图,连接OA,OC.
∵OP⊥CD,CD∥AB,
∴OP⊥AB,
∴CN=DN=8,AM=MB=10,
设OA=OC=r,OM=MN=a,
则有,
解得r=4,
故选:B.
【点睛】本题考查垂径定理,勾股定理等知识,解题的关键是学会利用参数构建方程组解决问题.
8.如图,△ABC内接于⊙O,AC为直径,半径OD∥BC,连接OB,AD.若∠AOB=α,则∠BAD的度数为( )
A. B. C. D.
【点拨】由AC为⊙O的直径,∠AOB=α,得∠C=,∠BOC=180°﹣α,由OD∥BC,∠DOC=∠C=,则∠BOD=∠BOC+∠DOC=180°﹣,所以∠BAD=∠BOD=90°﹣,于是得到问题的答案.
【解析】解:∵AC为⊙O的直径,∠AOB=α,
∴∠C=∠AOB=,∠BOC=180°﹣∠AOB=180°﹣α,
∵OD∥BC,
∴∠DOC=∠C=,
∴∠BOD=∠BOC+∠DOC=180°﹣α+=180°﹣,
∴∠BAD=∠BOD=(180°﹣)=90°﹣,
故选:C.
【点睛】此题重点考查平行线的性质、圆周角定理等知识,证明∠DOC=∠C=是解题的关键.
9.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=6,CE=4,则AE的长为( )
A.2 B.3 C. D.
【点拨】连接AC,根据圆内接四边形对角互补得到∠ABE=∠ADC,根据得到∠ABD=∠ACD结合角平分线得到∠ABE=∠ABD,即可得到:∠ADC=∠ACD,从而得到AC=AD,结合勾股定理即可得到答案;
【解析】解:连接AC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠ABE+∠ABC=180°,
∴∠ABE=∠ADC,
∵,
∴∠ABD=∠ACD,
∵BA平分∠DBE,
∴∠ABE=∠ABD,
∴∠ADC=∠ACD,
∴AC=AD,
∵AE⊥CB,AD=6,CE=4,
∴AC=6
∴,
故选:D.
【点睛】本题考查勾股定理及圆内接四边形对角互补,同弧所对的圆周角相等,等角对等边等知识,掌握这些知识是解题的关键.
10.如图在给定的⊙O中,弦AB的弦心距OH=6,CD=16,点E在弦CD上,且OE=ED=5,当△EAB面积的为最大时,DH的长为( )
A. B. C. D.
【点拨】过点E作EN⊥AB于点N,则点E轨迹为以点O为圆心,5为半径的圆,由OH⊥AB,EO+OH≥EN,则当点E,O,H三点共线时,EN最大,则△EAB面积最大,过点D作HO延长线的垂线,垂足为点M,过点O作OG⊥CD于点G,由垂径定理得,则GE=GD﹣ED=3,由勾股定理得OG=4,显然△MED≌△GEO,则MD=OG=4,ME=GE=3,故MH=14,在Rt△DMH中,由勾股定理即可求解.
【解析】解:过点E作EN⊥AB于点N,如图,
∵OE=5,
∴点E轨迹为以点O为圆心,5为半径的圆,
∵EO+OH≥EN,OH⊥AB,
∴如图:当点E,O,H三点共线时,EN最大,则△EAB面积最大,
过点O作OG⊥CD于点G,过点D作HO延长线的垂线,垂足为点M,
∴,
∴GE=GD﹣ED=3,
∴,
∵DM⊥EM,OG⊥CD,
∴∠M=∠OGE=90°,
∵EO=ED,∠MED=∠GEO,
∴△MED≌△GEO,
∴MD=OG=4,ME=GE=3,
∴MH=ME+OE+OH=3+5+6=14,
∴在Rt△DMH中,由勾股定理得:,
故选:B.
【点睛】本题考查了圆与三角形的综合题,涉及勾股定理,垂径定理,全等三角形的判定与性质,难度较大,解题的关键在于确定点E的轨迹以及当点E,O,H三点共线时,EN最大,则△EAB面积最大.
二、填空题:本题共6小题,每小题3分,共18分。
11.在半径为6的圆中,60°的圆心角所对的弧长为 2π .
【点拨】直接利用弧长公式计算即可.
【解析】解:l===2π.
故答案为:2π.
【点睛】本题考查了弧长的计算,解题的关键是牢记弧长的计算公式,难度不大.
12.在Rt△ABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的直径是 10 .
【点拨】首先根据勾股定理,得其斜边是5,即可得到答案.
【解析】解:∵∠C=90°,AC=6,BC=8,
∴BA==10,
∴这个三角形的外接圆的直径为10.
故答案为:10.
【点睛】本题考查三角形的外接圆与外心、勾股定理等知识,解题的关键是记住直角三角形的斜边就是外接圆的直径.
13.如图,在半径为10cm的⊙O中,AB=16cm,OC⊥AB于点C,则OC等于 6 cm.
【点拨】连接OA,如图,先利用垂径定理得到AC=BC=AB=8,然后根据勾股定理计算OC的长.
【解析】解:连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=8cm,
在Rt△OAC中,OC===6(cm).
故答案为6.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
14.半径为3的正六边形内接于⊙O,则正六边形的边长为 3 .
【点拨】由于正六边形可以分成六个边长的正三角形,而正多边形的半径即为正三角形的边长,同时也是正六边形ABCDEF的边长.
【解析】解:∵正六边形ABCDEF内接于⊙O,⊙O的半径为3,
而正六边形可以分成六个边长的正三角形,
∴正多边形的半径即为正三角形的边长,
∴正三角形的边长为3,
∴正六边形ABCDEF的边长为3,
故答案为:3.
【点睛】此题主要考查正多边形的计算问题,属于常规题,解题关键是根据正六边形可以分成六个边长的正三角形解答.
15.如图,等腰△ABC内接于⊙O,AB=AC,点D为劣弧BC上一点,∠ADC=60°,若CD=2BD=4,则四边形ABDC的面积为 9 .
【点拨】过点B作BE⊥CD的延长线于点E,先证明△ABC为等边三角形,再证明∠DBE=30°,根据CD=2BD=4,可得BD=2,所以,,然后根据四边形ABDC的面积=△BDC的面积+等边三角形ABC的面积,即可解决问题.
【解析】解:如图,过点B作BE⊥CD的延长线于点E,
∵∠ABC=∠ADC=60°,
又AB=AC,
∴△ABC为等边三角形,
∴∠ACB=∠ABC=60°,
∴∠ADB=∠ACB=∠ADC=60°,
∴∠BDC=120°,
∴∠BDE=60°,
∴∠DBE=30°,
∵CD=2BD=4,
∴BD=2,
∴,
∴,
∴△BDC的面积=,
在Rt△BEC中,,CE=CD+DE=4+1=5,
根据勾股定理得:BC2=BE2+CE2=3+25=28,
∴等边三角形ABC的面积=,
∴四边形ABDC的面积=△BDC的面积+等边三角形ABC的面积=.
∴四边形ABDC的面积为.
故答案为:.
【点睛】本题考查了三角形的外接圆与外心,圆周角定理,垂径定理,等边三角形的判定与性质,解决本题的关键是熟练运用圆周角定理,垂径定理.
16.如图,在半圆O中,直径AB=8,C,D是半圆上两点,P是直径上一点,若∠AOC=48°,∠AOD=72°,则PC+PD的最小值为 4 .
【点拨】将半圆O补充成一个整圆,过点C作AB的垂线交AB⊙O于点C′,连接C′D交AB于点P,连接PC、OC,连接OD,延长DO交⊙O于点E,连接C′E.根据垂径定理可知AB是CC′的垂直两平分线,从而可得PC+PD最小值为C′D的长度;根据圆周角定理求得∠CC′D=12°,从而求得∠APC′=78°,由对顶角的性质可知∠DPO=78°,再根据三角形内角和定理求得∠PDO=30°,由三角函数求出C′D即可.
【解析】解:将半圆O补充成一个整圆,过点C作AB的垂线交AB⊙O于点C′,连接C′D交AB于点P,连接PC、OC,连接OD,延长DO交⊙O于点E,连接C′E.
∵AB为直径,AB⊥CC′,
∴AB是CC′的垂直两平分线,
∴PC′=PC,
∴PC′+PD=PC+PD=C′D,
∴PC+PD最小值为C′D的长度,
∵∠AOC=48°,∠AOD=72°,
∴∠COD=∠AOD﹣∠AOC=72°﹣48°=24°,
∴∠CC′D=∠COD=×24°=12°,
∴∠APC′=90°﹣∠CC′D=90°﹣12°=78°,
∴∠DPO=∠APC′=78°,
∴∠PDO=180°﹣∠DPO﹣∠AOD=180°﹣78°﹣72°=30°,
∵DE为直径,
∴∠DC′E=90°,DE=AB=8,
∴C′D=DE cos∠PDO=8×=4,
∴PC+PD的最小值为4.
故答案为:4.
【点睛】本题考查圆周角定理、垂径定理、轴对称﹣最短路线问题,作点C的对称点并将PC+PD的最小值转化为线段,掌握圆周角定理、垂径定理、三角形内角和定理、特殊角的三角函数是解题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,⊙O的弦AB,CD相交于点E,且AB=CD,求证:EB=ED.
【点拨】连接AC,利用在同圆或等圆中,等弦对等弧,同弧或等弧所对的圆周角相等,得出∠A=∠C;利用等腰三角形的判定定理得到EA=EC,利用等式的性质即可得出结论.
【解析】证明:连接AC,如图,
∵AB=CD,
∴.
∴.
即.
∴∠A=∠C.
∴EA=EC.
∴AB﹣EA=CD﹣EC.即EB=ED.
【点睛】本题主要考查了圆心角,弧,弦的关系,圆周角定理及其推论,等腰三角形的判定,等式的性质,连接AC,利用等弧所对的圆周角相等得出∠A=∠C是解题的关键.
18.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣1,3),B(﹣3,0),C(﹣1,0),把△ABC绕点C按顺时针方向旋转90°后得到△A1B1C.(每个方格的边长均为1个单位)
(1)画出△A1B1C并直接写出:
A1的坐标为 (2,0) ,
B1的坐标为 (﹣1,2) ;
(2)判断直线AB与直线A1B1的位置关系为 垂直 .
【点拨】(1)利用网格特点和旋转的性质画出点A、B的对应点A1、B1,然后写出点A1、B1的坐标;
(2)根据旋转的性质判断.
【解析】解:(1)如图,△A1B1C为所作,A1的坐标为(2,0),B1的坐标为(﹣1,2);
故答案为:(2,0);(﹣1,2);
(2)因为△ABC绕点C按顺时针方向旋转90°后得到△A1B1C,
所以AB绕点C按顺时针方向旋转90°后得到A1B1,
即直线AB与直线A1B1垂直.
故答案为:垂直.
【点睛】本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
19.如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°.
(1)求∠CAD的度数;
(2)若⊙O的半径为1,求图中阴影部分的面积.
【点拨】(1)根据圆周角定理得到∠ACD=90°,∠ADC=∠ABC=60°,根据直角三角形的性质计算即可;
(2)连接OC,过O作OQ⊥AC于Q,根据勾股定理求出AQ,再根据垂径定理求出AC,根据圆周角定理求出∠AOC,根据扇形面积公式、三角形的面积公式计算,得到答案.
【解析】解:(1)∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠ADC=∠ABC=60°,
∴∠CAD=90°﹣∠ADC=30°;
(2)连接OC,过O作OQ⊥AC于Q,
∵∠CAD=30°,⊙O的半径为1,
∴OQ=OA=,
由勾股定理得:AQ===,
∵OQ⊥AC,
∴AC=2AQ=,
由圆周角定理得:∠AOC=2∠ABC=120°,
∴S阴影部分=S扇形AOC﹣S△AOC
=﹣××
=﹣.
【点睛】本题考查的是三角形的外接圆与外心,掌握圆周角定理、扇形面积公式是解题的关键.
20.如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接BC,作OF⊥BC于点F,求OF的长.
【点拨】(1)连接OD,如图,设⊙O的半径长为r,先根据垂径定理得到DE=CE=4,再利用勾股定理得到(r﹣2)2+42=r2,然后解方程即可;
(2)先利用勾股定理计算出BC=4,再根据垂径定理得到BF=CF=2,然后利用勾股定理可计算出OF的长.
【解析】解:(1)连接OD,如图,设⊙O的半径长为r,
∵AB⊥CD,
∴∠OED=90°,DE=CE=CD=×8=4,
在Rt△ODE中,∵OE=r﹣2,OD=r,DE=4,
∴(r﹣2)2+42=r2,
解得r=5,
即⊙O的半径长为5;
(2)在Rt△BCE中,∵CE=4,BE=AB﹣AE=8,
∴BC==4,
∵OF⊥BC,
∴BF=CF=BC=2,∠OFB=90°,
在Rt△OBF中,OF===,
即OF的长为.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
21.如图,四边形ABCD内接于一圆,连结AC、BD.
(1)若∠DAB=60°,∠ACB=70°,求∠ABD的度数.
(2)若AC为直径,C为的中点,请探究∠DAB与∠ACB之间的关系.
【点拨】(1)根据圆周角定理求出∠ADB,再根据三角形内角和定理求出∠ABD;
(2)根据圆周角定理得到∠CAB=∠DAB,∠ABC=90°,根据直角三角形的两锐角互余解答即可.
【解析】解:(1)∵∠ACB=70°,
∴∠ADB=∠ACB=70°,
∵∠DAB=60°,
∴∠ABD=180°﹣70°﹣60°=50°;
(2)∵C为的中点,
∴∠CAB=∠CAD=∠DAB,
∵AC为直径,
∴∠ABC=90°,
∴∠CAB+∠ACB=90°,
∴∠DAB+∠ACB=90°.
【点睛】本题考查的是圆周角定理、三角形内角和定理,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等是解题的关键.
22.如图,在半圆O中,直径AB=6,点C在上,连接BC,弦BD平分∠ABC,连接OD.
(1)求证:OD∥BC;
(2)连接OC,AD.若OC∥AD,求BD的长.
【点拨】(1)利用角平分线的定义结合平行线的性质和判定即可得证;
(2)先证明△AOD是等边三角形,再利用圆周角定理和勾股定理即可求解.
【解析】(1)证明:∵弦BD平分∠ABC,
∴∠ABD=∠CBD,
∵OB=OD,
∴∠ABD=∠ODB,
∴∠ODB=∠CBD,
∴OD∥BC;
(2)解:∵OC∥AD,
∴∠BAD=∠BOC,
∵∠BOD=2∠BAD,
∴∠BOD=2∠BOC,
∴∠BOC=∠COD,
∵∠ABD=∠CBD,
∴∠AOD=∠COD,
∴∠BOC=∠AOD=∠COD=60°,
∵OA=OD,AB=6,
∴△AOD是等边三角形,
∴,
∵AB是半圆的直径,
∴∠ADB=90°,
∴BD===3.
【点睛】本题考查了圆周角定理,等腰三角形的判定和性质,熟知以上知识是解题的关键.
23.在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交直线AC于点E,连结BE.
小明:根据题意,我画出了如图1的情况;
小丽:小明,你的思考不够全面,我认为还有其他的情况,若∠BAC为钝角,我发现圆与直线AC的交点在线段CA的延长线上;
小明:哦...我明白了!
(1)在图1中求证:点D是边BC的中点;
(2)记∠ABE的度数为α.求出∠C的度数(用α表示).
【点拨】(1)连接AD,根据直径所对的圆周角是直角得AD⊥BC,再根据等腰三角形的性质可得出结论;
(2)当△ABC是锐角三角形时,点E在边AC上,根据∠AEB=90°得∠BAC=90°﹣α,再根据AB=AC可得出∠C的度数;当△ABC是钝角三角形时,点E在CA的延长线上,根据∠AEB=90°得∠BAC=90°+α,再根据AB=AC可得出∠C的度数;当△ABC是直角三角形时,点E与点A重合,此时α=0°,∠C=45°.综上所述即可得出答案.
【解析】(1)证明:连接AD,如图1所示:
∵AB是⊙O的直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
即点D是边BC的中点;
(2)当△ABC是锐角三角形时,点E在边AC上,如图1所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠BAC=90°﹣α,
∵AB=AC,
∴∠C=∠ABC=(180°﹣∠BAC)=45°+;
当△ABC是钝角三角形时,点E在CA的延长线上,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠BAC=90°+α,
∵AB=AC,
∴∠C=∠ABC=(180°﹣∠BAC)=45°﹣;
当△ABC是直角三角形时,点E与点A重合,
此时α=0°,∠C=45°.
综上所述:∠C的度数是45°+或45°﹣或45°.
【点睛】此题主要考查了圆周角定理,等腰三角形的性质,熟练掌握圆周角定理,等腰三角形的性质是解决问题的关键.
24.已知AB是⊙O的直径,点C在⊙O上,D为弧BC的中点.
(1)如图①,连接AC,AD,OD.求证:OD∥AC;
(2)如图②,过点D作DE⊥AB交⊙O于点E,直径EF交AC于点G,若G为AC中点,
①求证:∠BOD=45°;
②若⊙O的半径为2,求AC的长.
【点拨】(1)根据圆周角定理,由=得到∠BAD=∠CAD,加上∠BAD=∠ODA,所以∠CAD=∠ODA,然后根据平行线的判定方法得到结论;
(2)①先根据垂径定理得到EF⊥AC,再利用OD∥AC得到DO⊥EF,所以∠DOE=90°,接着利用垂径定理得到=,然后根据圆周角定理得到∠BOD=∠DOE=45°;
②由OD∥AC得到∠CAB=∠BOD=45°,再根据垂径定理得到AG=CG,然后根据等腰直角三角形的性质求出AG=,从而得到AC的长.
【解析】(1)证明:∵D为弧BC的中点,
∴=,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC;
(2)解:①∵G为AC中点,EF为直径,
∴EF⊥AC,
∵OD∥AC,
∴DO⊥EF,
∴∠DOE=90°,
∵AB是⊙O的直径,DE⊥AB,
∴=,
∴∠BOD=∠DOE=45°;
②∵OD∥AC,
∴∠CAB=∠BOD=45°,
∵OG⊥AC,
∴AG=CG,△AOG是等腰直角三角形,
∴AG=×2=,
∴AC=2AG=2.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第3章 圆 单元检测能力提升卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=25°,则∠AOC的大小是( )
A.25° B.50° C.65° D.75°
2.下列说法中正确的是( )
A.所对圆心角相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
3.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
4.如图,△ABC中,∠A=50°,以AB为直径的⊙O分别与BC,AC交于点D,E,且BD=CD,连接BE,DE,则∠BED的大小为( )
A.25° B.30° C.35° D.50°
5.如图,点A在⊙O上,OD⊥弦BC于点D.若∠BAC=45°,OD=1,则BC=( )
、
A. B.2 C.2 D.
6.如图,AB、CD是⊙O的两条直径,点E是弧BD的中点,连接AC、BE,若∠ACD=20°,则∠ABE的度数( )
A.40° B.44° C.50° D.55°
7.如图,在⊙O中,弦AB∥CD,OP⊥CD,OM=MN,AB=20,CD=16,则⊙O的半径为( )
A. B. C. D.
8.如图,△ABC内接于⊙O,AC为直径,半径OD∥BC,连接OB,AD.若∠AOB=α,则∠BAD的度数为( )
A. B. C. D.
9.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=6,CE=4,则AE的长为( )
A.2 B.3 C. D.
10.如图在给定的⊙O中,弦AB的弦心距OH=6,CD=16,点E在弦CD上,且OE=ED=5,当△EAB面积的为最大时,DH的长为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.在半径为6的圆中,60°的圆心角所对的弧长为 .
12.在Rt△ABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的直径是 .
13.如图,在半径为10cm的⊙O中,AB=16cm,OC⊥AB于点C,则OC等于 cm.
14.半径为3的正六边形内接于⊙O,则正六边形的边长为 .
15.如图,等腰△ABC内接于⊙O,AB=AC,点D为劣弧BC上一点,∠ADC=60°,若CD=2BD=4,则四边形ABDC的面积为 .
16.如图,在半圆O中,直径AB=8,C,D是半圆上两点,P是直径上一点,若∠AOC=48°,∠AOD=72°,则PC+PD的最小值为 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,⊙O的弦AB,CD相交于点E,且AB=CD,求证:EB=ED.
18.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣1,3),B(﹣3,0),C(﹣1,0),把△ABC绕点C按顺时针方向旋转90°后得到△A1B1C.(每个方格的边长均为1个单位)
(1)画出△A1B1C并直接写出:
A1的坐标为 ,
B1的坐标为 ;
(2)判断直线AB与直线A1B1的位置关系为 .
19.如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°.
(1)求∠CAD的度数;
(2)若⊙O的半径为1,求图中阴影部分的面积.
20.如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接BC,作OF⊥BC于点F,求OF的长.
21.如图,四边形ABCD内接于一圆,连结AC、BD.
(1)若∠DAB=60°,∠ACB=70°,求∠ABD的度数.
(2)若AC为直径,C为的中点,请探究∠DAB与∠ACB之间的关系.
22.如图,在半圆O中,直径AB=6,点C在上,连接BC,弦BD平分∠ABC,连接OD.
(1)求证:OD∥BC;
(2)连接OC,AD.若OC∥AD,求BD的长.
23.在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交直线AC于点E,连结BE.
小明:根据题意,我画出了如图1的情况;
小丽:小明,你的思考不够全面,我认为还有其他的情况,若∠BAC为钝角,我发现圆与直线AC的交点在线段CA的延长线上;
小明:哦...我明白了!
(1)在图1中求证:点D是边BC的中点;
(2)记∠ABE的度数为α.求出∠C的度数(用α表示).
24.已知AB是⊙O的直径,点C在⊙O上,D为弧BC的中点.
(1)如图①,连接AC,AD,OD.求证:OD∥AC;
(2)如图②,过点D作DE⊥AB交⊙O于点E,直径EF交AC于点G,若G为AC中点,
①求证:∠BOD=45°;
②若⊙O的半径为2,求AC的长.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=25°,则∠AOC的大小是( )
A.25° B.50° C.65° D.75°
【点拨】利用圆周角定理解决问题即可.
【解析】解:∵∠AOC=2∠ABC,∠ABC=25°,
∴∠AOC=50°,
故选:B.
【点睛】本题考查圆周角定理,解题的关键是记住在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2.下列说法中正确的是( )
A.所对圆心角相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
【点拨】根据等弧的定义垂径定理,圆周角定理一一判断即可.
【解析】解:A.在同圆或等圆中,所对圆心角相等的两条弧是等弧,故A错误,本选项不符合题意;
B.平分弦的直径垂直于弦,此弦不能是直径,故B错误,本选项不符合题意;
C.在同圆或等圆中,相等的圆心角所对的弧相等,故C错误,本选项不符合题意;
D.经过圆心的每一条直线都是圆的对称轴,故D正确,本选项符合题意.
故选:D.
【点睛】本题考查圆周角定理,垂径定理,轴对称等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
3.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
【点拨】连接OA,OB,根据圆周角定理得到∠AOB=2∠ADB=36°,于是得到结论.
【解析】解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数==10,
故选:A.
【点睛】本题考查了正多边形与圆,圆周角定理,正确的理解题意是解题的关键.
4.如图,△ABC中,∠A=50°,以AB为直径的⊙O分别与BC,AC交于点D,E,且BD=CD,连接BE,DE,则∠BED的大小为( )
A.25° B.30° C.35° D.50°
【点拨】连接AD,证明AB=AC,利用三线合一的性质求出∠BAD即可解决问题.
【解析】解:连接AD,
∵AB是直径,
∴∠ADB=90°,即AD⊥BC,
∵BD=DC,
∴AB=AC,
∴∠BAD=∠BAC=25°,
∴∠BED=∠BAD=25°.
故选:A.
【点睛】本题考查圆周角定理,等腰三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.如图,点A在⊙O上,OD⊥弦BC于点D.若∠BAC=45°,OD=1,则BC=( )
A. B.2 C.2 D.
【点拨】利用圆周角定理得到∠BOC=90°,利用等腰三角形的性质得∠OBC=∠OCB=45°,再根据垂径定理得到BD=CD,根据等腰三角形的判定与性质求出BD,从而得到BC的长.
【解析】解:∵∠BAC=45°,
∴∠BOC=2∠BAC=2×45°=90°,
∵OB=OC,
∴∠OBC=∠OCB=45°,
∵OD⊥BC,
∴BD=CD,∠BOD=180°﹣90°﹣45°=45°=∠OBD,
∴BD=OD=2,
∴BC=2BD=2.
故选:C.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.
6.如图,AB、CD是⊙O的两条直径,点E是弧BD的中点,连接AC、BE,若∠ACD=20°,则∠ABE的度数( )
A.40° B.44° C.50° D.55°
【点拨】连接OE,利用圆周角定理求得∠AOD=40°,再求得∠DOE=∠BOE=70°,根据等边对等角即可求解.
【解析】解:连接OE,如图所示:
∵∠ACD=20°,
∴∠AOD=2∠ACD=40°,
∵点E是弧BD的中点,
∴,
∵OE=OB,
∴,
故选:D.
【点睛】本题主要考查圆周角定理及等腰三角形的判定和性质,熟练掌握圆周角定理是解题的关键.
7.如图,在⊙O中,弦AB∥CD,OP⊥CD,OM=MN,AB=20,CD=16,则⊙O的半径为( )
A. B. C. D.
【点拨】如图,连接OA,OC.设OA=OC=r,OM=MN=a,构建方程组求出r即可.
【解析】解:如图,连接OA,OC.
∵OP⊥CD,CD∥AB,
∴OP⊥AB,
∴CN=DN=8,AM=MB=10,
设OA=OC=r,OM=MN=a,
则有,
解得r=4,
故选:B.
【点睛】本题考查垂径定理,勾股定理等知识,解题的关键是学会利用参数构建方程组解决问题.
8.如图,△ABC内接于⊙O,AC为直径,半径OD∥BC,连接OB,AD.若∠AOB=α,则∠BAD的度数为( )
A. B. C. D.
【点拨】由AC为⊙O的直径,∠AOB=α,得∠C=,∠BOC=180°﹣α,由OD∥BC,∠DOC=∠C=,则∠BOD=∠BOC+∠DOC=180°﹣,所以∠BAD=∠BOD=90°﹣,于是得到问题的答案.
【解析】解:∵AC为⊙O的直径,∠AOB=α,
∴∠C=∠AOB=,∠BOC=180°﹣∠AOB=180°﹣α,
∵OD∥BC,
∴∠DOC=∠C=,
∴∠BOD=∠BOC+∠DOC=180°﹣α+=180°﹣,
∴∠BAD=∠BOD=(180°﹣)=90°﹣,
故选:C.
【点睛】此题重点考查平行线的性质、圆周角定理等知识,证明∠DOC=∠C=是解题的关键.
9.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=6,CE=4,则AE的长为( )
A.2 B.3 C. D.
【点拨】连接AC,根据圆内接四边形对角互补得到∠ABE=∠ADC,根据得到∠ABD=∠ACD结合角平分线得到∠ABE=∠ABD,即可得到:∠ADC=∠ACD,从而得到AC=AD,结合勾股定理即可得到答案;
【解析】解:连接AC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∵∠ABE+∠ABC=180°,
∴∠ABE=∠ADC,
∵,
∴∠ABD=∠ACD,
∵BA平分∠DBE,
∴∠ABE=∠ABD,
∴∠ADC=∠ACD,
∴AC=AD,
∵AE⊥CB,AD=6,CE=4,
∴AC=6
∴,
故选:D.
【点睛】本题考查勾股定理及圆内接四边形对角互补,同弧所对的圆周角相等,等角对等边等知识,掌握这些知识是解题的关键.
10.如图在给定的⊙O中,弦AB的弦心距OH=6,CD=16,点E在弦CD上,且OE=ED=5,当△EAB面积的为最大时,DH的长为( )
A. B. C. D.
【点拨】过点E作EN⊥AB于点N,则点E轨迹为以点O为圆心,5为半径的圆,由OH⊥AB,EO+OH≥EN,则当点E,O,H三点共线时,EN最大,则△EAB面积最大,过点D作HO延长线的垂线,垂足为点M,过点O作OG⊥CD于点G,由垂径定理得,则GE=GD﹣ED=3,由勾股定理得OG=4,显然△MED≌△GEO,则MD=OG=4,ME=GE=3,故MH=14,在Rt△DMH中,由勾股定理即可求解.
【解析】解:过点E作EN⊥AB于点N,如图,
∵OE=5,
∴点E轨迹为以点O为圆心,5为半径的圆,
∵EO+OH≥EN,OH⊥AB,
∴如图:当点E,O,H三点共线时,EN最大,则△EAB面积最大,
过点O作OG⊥CD于点G,过点D作HO延长线的垂线,垂足为点M,
∴,
∴GE=GD﹣ED=3,
∴,
∵DM⊥EM,OG⊥CD,
∴∠M=∠OGE=90°,
∵EO=ED,∠MED=∠GEO,
∴△MED≌△GEO,
∴MD=OG=4,ME=GE=3,
∴MH=ME+OE+OH=3+5+6=14,
∴在Rt△DMH中,由勾股定理得:,
故选:B.
【点睛】本题考查了圆与三角形的综合题,涉及勾股定理,垂径定理,全等三角形的判定与性质,难度较大,解题的关键在于确定点E的轨迹以及当点E,O,H三点共线时,EN最大,则△EAB面积最大.
二、填空题:本题共6小题,每小题3分,共18分。
11.在半径为6的圆中,60°的圆心角所对的弧长为 2π .
【点拨】直接利用弧长公式计算即可.
【解析】解:l===2π.
故答案为:2π.
【点睛】本题考查了弧长的计算,解题的关键是牢记弧长的计算公式,难度不大.
12.在Rt△ABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的直径是 10 .
【点拨】首先根据勾股定理,得其斜边是5,即可得到答案.
【解析】解:∵∠C=90°,AC=6,BC=8,
∴BA==10,
∴这个三角形的外接圆的直径为10.
故答案为:10.
【点睛】本题考查三角形的外接圆与外心、勾股定理等知识,解题的关键是记住直角三角形的斜边就是外接圆的直径.
13.如图,在半径为10cm的⊙O中,AB=16cm,OC⊥AB于点C,则OC等于 6 cm.
【点拨】连接OA,如图,先利用垂径定理得到AC=BC=AB=8,然后根据勾股定理计算OC的长.
【解析】解:连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=8cm,
在Rt△OAC中,OC===6(cm).
故答案为6.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
14.半径为3的正六边形内接于⊙O,则正六边形的边长为 3 .
【点拨】由于正六边形可以分成六个边长的正三角形,而正多边形的半径即为正三角形的边长,同时也是正六边形ABCDEF的边长.
【解析】解:∵正六边形ABCDEF内接于⊙O,⊙O的半径为3,
而正六边形可以分成六个边长的正三角形,
∴正多边形的半径即为正三角形的边长,
∴正三角形的边长为3,
∴正六边形ABCDEF的边长为3,
故答案为:3.
【点睛】此题主要考查正多边形的计算问题,属于常规题,解题关键是根据正六边形可以分成六个边长的正三角形解答.
15.如图,等腰△ABC内接于⊙O,AB=AC,点D为劣弧BC上一点,∠ADC=60°,若CD=2BD=4,则四边形ABDC的面积为 9 .
【点拨】过点B作BE⊥CD的延长线于点E,先证明△ABC为等边三角形,再证明∠DBE=30°,根据CD=2BD=4,可得BD=2,所以,,然后根据四边形ABDC的面积=△BDC的面积+等边三角形ABC的面积,即可解决问题.
【解析】解:如图,过点B作BE⊥CD的延长线于点E,
∵∠ABC=∠ADC=60°,
又AB=AC,
∴△ABC为等边三角形,
∴∠ACB=∠ABC=60°,
∴∠ADB=∠ACB=∠ADC=60°,
∴∠BDC=120°,
∴∠BDE=60°,
∴∠DBE=30°,
∵CD=2BD=4,
∴BD=2,
∴,
∴,
∴△BDC的面积=,
在Rt△BEC中,,CE=CD+DE=4+1=5,
根据勾股定理得:BC2=BE2+CE2=3+25=28,
∴等边三角形ABC的面积=,
∴四边形ABDC的面积=△BDC的面积+等边三角形ABC的面积=.
∴四边形ABDC的面积为.
故答案为:.
【点睛】本题考查了三角形的外接圆与外心,圆周角定理,垂径定理,等边三角形的判定与性质,解决本题的关键是熟练运用圆周角定理,垂径定理.
16.如图,在半圆O中,直径AB=8,C,D是半圆上两点,P是直径上一点,若∠AOC=48°,∠AOD=72°,则PC+PD的最小值为 4 .
【点拨】将半圆O补充成一个整圆,过点C作AB的垂线交AB⊙O于点C′,连接C′D交AB于点P,连接PC、OC,连接OD,延长DO交⊙O于点E,连接C′E.根据垂径定理可知AB是CC′的垂直两平分线,从而可得PC+PD最小值为C′D的长度;根据圆周角定理求得∠CC′D=12°,从而求得∠APC′=78°,由对顶角的性质可知∠DPO=78°,再根据三角形内角和定理求得∠PDO=30°,由三角函数求出C′D即可.
【解析】解:将半圆O补充成一个整圆,过点C作AB的垂线交AB⊙O于点C′,连接C′D交AB于点P,连接PC、OC,连接OD,延长DO交⊙O于点E,连接C′E.
∵AB为直径,AB⊥CC′,
∴AB是CC′的垂直两平分线,
∴PC′=PC,
∴PC′+PD=PC+PD=C′D,
∴PC+PD最小值为C′D的长度,
∵∠AOC=48°,∠AOD=72°,
∴∠COD=∠AOD﹣∠AOC=72°﹣48°=24°,
∴∠CC′D=∠COD=×24°=12°,
∴∠APC′=90°﹣∠CC′D=90°﹣12°=78°,
∴∠DPO=∠APC′=78°,
∴∠PDO=180°﹣∠DPO﹣∠AOD=180°﹣78°﹣72°=30°,
∵DE为直径,
∴∠DC′E=90°,DE=AB=8,
∴C′D=DE cos∠PDO=8×=4,
∴PC+PD的最小值为4.
故答案为:4.
【点睛】本题考查圆周角定理、垂径定理、轴对称﹣最短路线问题,作点C的对称点并将PC+PD的最小值转化为线段,掌握圆周角定理、垂径定理、三角形内角和定理、特殊角的三角函数是解题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,⊙O的弦AB,CD相交于点E,且AB=CD,求证:EB=ED.
【点拨】连接AC,利用在同圆或等圆中,等弦对等弧,同弧或等弧所对的圆周角相等,得出∠A=∠C;利用等腰三角形的判定定理得到EA=EC,利用等式的性质即可得出结论.
【解析】证明:连接AC,如图,
∵AB=CD,
∴.
∴.
即.
∴∠A=∠C.
∴EA=EC.
∴AB﹣EA=CD﹣EC.即EB=ED.
【点睛】本题主要考查了圆心角,弧,弦的关系,圆周角定理及其推论,等腰三角形的判定,等式的性质,连接AC,利用等弧所对的圆周角相等得出∠A=∠C是解题的关键.
18.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣1,3),B(﹣3,0),C(﹣1,0),把△ABC绕点C按顺时针方向旋转90°后得到△A1B1C.(每个方格的边长均为1个单位)
(1)画出△A1B1C并直接写出:
A1的坐标为 (2,0) ,
B1的坐标为 (﹣1,2) ;
(2)判断直线AB与直线A1B1的位置关系为 垂直 .
【点拨】(1)利用网格特点和旋转的性质画出点A、B的对应点A1、B1,然后写出点A1、B1的坐标;
(2)根据旋转的性质判断.
【解析】解:(1)如图,△A1B1C为所作,A1的坐标为(2,0),B1的坐标为(﹣1,2);
故答案为:(2,0);(﹣1,2);
(2)因为△ABC绕点C按顺时针方向旋转90°后得到△A1B1C,
所以AB绕点C按顺时针方向旋转90°后得到A1B1,
即直线AB与直线A1B1垂直.
故答案为:垂直.
【点睛】本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
19.如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°.
(1)求∠CAD的度数;
(2)若⊙O的半径为1,求图中阴影部分的面积.
【点拨】(1)根据圆周角定理得到∠ACD=90°,∠ADC=∠ABC=60°,根据直角三角形的性质计算即可;
(2)连接OC,过O作OQ⊥AC于Q,根据勾股定理求出AQ,再根据垂径定理求出AC,根据圆周角定理求出∠AOC,根据扇形面积公式、三角形的面积公式计算,得到答案.
【解析】解:(1)∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠ADC=∠ABC=60°,
∴∠CAD=90°﹣∠ADC=30°;
(2)连接OC,过O作OQ⊥AC于Q,
∵∠CAD=30°,⊙O的半径为1,
∴OQ=OA=,
由勾股定理得:AQ===,
∵OQ⊥AC,
∴AC=2AQ=,
由圆周角定理得:∠AOC=2∠ABC=120°,
∴S阴影部分=S扇形AOC﹣S△AOC
=﹣××
=﹣.
【点睛】本题考查的是三角形的外接圆与外心,掌握圆周角定理、扇形面积公式是解题的关键.
20.如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)求⊙O的半径长;
(2)连接BC,作OF⊥BC于点F,求OF的长.
【点拨】(1)连接OD,如图,设⊙O的半径长为r,先根据垂径定理得到DE=CE=4,再利用勾股定理得到(r﹣2)2+42=r2,然后解方程即可;
(2)先利用勾股定理计算出BC=4,再根据垂径定理得到BF=CF=2,然后利用勾股定理可计算出OF的长.
【解析】解:(1)连接OD,如图,设⊙O的半径长为r,
∵AB⊥CD,
∴∠OED=90°,DE=CE=CD=×8=4,
在Rt△ODE中,∵OE=r﹣2,OD=r,DE=4,
∴(r﹣2)2+42=r2,
解得r=5,
即⊙O的半径长为5;
(2)在Rt△BCE中,∵CE=4,BE=AB﹣AE=8,
∴BC==4,
∵OF⊥BC,
∴BF=CF=BC=2,∠OFB=90°,
在Rt△OBF中,OF===,
即OF的长为.
【点睛】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
21.如图,四边形ABCD内接于一圆,连结AC、BD.
(1)若∠DAB=60°,∠ACB=70°,求∠ABD的度数.
(2)若AC为直径,C为的中点,请探究∠DAB与∠ACB之间的关系.
【点拨】(1)根据圆周角定理求出∠ADB,再根据三角形内角和定理求出∠ABD;
(2)根据圆周角定理得到∠CAB=∠DAB,∠ABC=90°,根据直角三角形的两锐角互余解答即可.
【解析】解:(1)∵∠ACB=70°,
∴∠ADB=∠ACB=70°,
∵∠DAB=60°,
∴∠ABD=180°﹣70°﹣60°=50°;
(2)∵C为的中点,
∴∠CAB=∠CAD=∠DAB,
∵AC为直径,
∴∠ABC=90°,
∴∠CAB+∠ACB=90°,
∴∠DAB+∠ACB=90°.
【点睛】本题考查的是圆周角定理、三角形内角和定理,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等是解题的关键.
22.如图,在半圆O中,直径AB=6,点C在上,连接BC,弦BD平分∠ABC,连接OD.
(1)求证:OD∥BC;
(2)连接OC,AD.若OC∥AD,求BD的长.
【点拨】(1)利用角平分线的定义结合平行线的性质和判定即可得证;
(2)先证明△AOD是等边三角形,再利用圆周角定理和勾股定理即可求解.
【解析】(1)证明:∵弦BD平分∠ABC,
∴∠ABD=∠CBD,
∵OB=OD,
∴∠ABD=∠ODB,
∴∠ODB=∠CBD,
∴OD∥BC;
(2)解:∵OC∥AD,
∴∠BAD=∠BOC,
∵∠BOD=2∠BAD,
∴∠BOD=2∠BOC,
∴∠BOC=∠COD,
∵∠ABD=∠CBD,
∴∠AOD=∠COD,
∴∠BOC=∠AOD=∠COD=60°,
∵OA=OD,AB=6,
∴△AOD是等边三角形,
∴,
∵AB是半圆的直径,
∴∠ADB=90°,
∴BD===3.
【点睛】本题考查了圆周角定理,等腰三角形的判定和性质,熟知以上知识是解题的关键.
23.在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交直线AC于点E,连结BE.
小明:根据题意,我画出了如图1的情况;
小丽:小明,你的思考不够全面,我认为还有其他的情况,若∠BAC为钝角,我发现圆与直线AC的交点在线段CA的延长线上;
小明:哦...我明白了!
(1)在图1中求证:点D是边BC的中点;
(2)记∠ABE的度数为α.求出∠C的度数(用α表示).
【点拨】(1)连接AD,根据直径所对的圆周角是直角得AD⊥BC,再根据等腰三角形的性质可得出结论;
(2)当△ABC是锐角三角形时,点E在边AC上,根据∠AEB=90°得∠BAC=90°﹣α,再根据AB=AC可得出∠C的度数;当△ABC是钝角三角形时,点E在CA的延长线上,根据∠AEB=90°得∠BAC=90°+α,再根据AB=AC可得出∠C的度数;当△ABC是直角三角形时,点E与点A重合,此时α=0°,∠C=45°.综上所述即可得出答案.
【解析】(1)证明:连接AD,如图1所示:
∵AB是⊙O的直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
即点D是边BC的中点;
(2)当△ABC是锐角三角形时,点E在边AC上,如图1所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠BAC=90°﹣α,
∵AB=AC,
∴∠C=∠ABC=(180°﹣∠BAC)=45°+;
当△ABC是钝角三角形时,点E在CA的延长线上,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠BAC=90°+α,
∵AB=AC,
∴∠C=∠ABC=(180°﹣∠BAC)=45°﹣;
当△ABC是直角三角形时,点E与点A重合,
此时α=0°,∠C=45°.
综上所述:∠C的度数是45°+或45°﹣或45°.
【点睛】此题主要考查了圆周角定理,等腰三角形的性质,熟练掌握圆周角定理,等腰三角形的性质是解决问题的关键.
24.已知AB是⊙O的直径,点C在⊙O上,D为弧BC的中点.
(1)如图①,连接AC,AD,OD.求证:OD∥AC;
(2)如图②,过点D作DE⊥AB交⊙O于点E,直径EF交AC于点G,若G为AC中点,
①求证:∠BOD=45°;
②若⊙O的半径为2,求AC的长.
【点拨】(1)根据圆周角定理,由=得到∠BAD=∠CAD,加上∠BAD=∠ODA,所以∠CAD=∠ODA,然后根据平行线的判定方法得到结论;
(2)①先根据垂径定理得到EF⊥AC,再利用OD∥AC得到DO⊥EF,所以∠DOE=90°,接着利用垂径定理得到=,然后根据圆周角定理得到∠BOD=∠DOE=45°;
②由OD∥AC得到∠CAB=∠BOD=45°,再根据垂径定理得到AG=CG,然后根据等腰直角三角形的性质求出AG=,从而得到AC的长.
【解析】(1)证明:∵D为弧BC的中点,
∴=,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC;
(2)解:①∵G为AC中点,EF为直径,
∴EF⊥AC,
∵OD∥AC,
∴DO⊥EF,
∴∠DOE=90°,
∵AB是⊙O的直径,DE⊥AB,
∴=,
∴∠BOD=∠DOE=45°;
②∵OD∥AC,
∴∠CAB=∠BOD=45°,
∵OG⊥AC,
∴AG=CG,△AOG是等腰直角三角形,
∴AG=×2=,
∴AC=2AG=2.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
